扩展功能
文章信息
- 孙海波, 刘鹏飞, 刘保东, 徐伟博, 高猛
- SUN Hai-bo, LIU Peng-fei, LIU Bao-dong, XU Wei-bo, GAO Meng
- 不同断面线形波纹钢管涵结构力学性能研究
- Study on Structural Mechanical Performance of Corrugated Steel Pipe Culverts with Different Cross-section Shapes
- 公路交通科技, 2015, Vol. 31 (10): 75-81
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (10): 75-81
- 10.3969/j.issn.1002-0268.2015.10.013
-
文章历史
- 收稿日期: 2015-06-05
2. 北京交通大学 土木建筑工程学院, 北京 100044
2. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
覆土波纹钢板桥涵在国内的应用不断增加,并逐渐作为小桥涵的替代结构物应用于道路工程中,该类型结构的断面线形非常丰富,可适用于不同的地质、地形条件,满足不同的使用功能。通常采用的闭口形式线形主要包括:圆形、水平椭圆形、竖向椭圆形、管拱形、梨形等。圆形管涵在各种功能状况下均使用良好,尤其适用于埋深较大的情况下;管拱形结构具有水力优势,在填土较薄或在圆管不能满足最小填土高度的情况下适宜采用,且管拱形结构下部曲线较为平顺,与地表有更大的接触面积,一定程度上减小了局部地表压力,而且具有作为行人车辆通道的作用。
1999年,杨猛阐述了波纹钢管涵洞的形式、类型和构造特点,并针对其优点,就设计、施工工艺、原材料以及经济性等方面,第一次对公路波纹钢结构涵洞应用的可行性进行了探讨[1]。目前国内对覆土波纹钢管涵的研究以圆管涵为主。2000年,中交第一公路勘察设计院依据1997和1998年在青藏公路多年冻土区上修建3道试验用波纹钢圆管涵,得出波纹钢管涵具有自重轻、运输方便、施工简单且施工工期短和变形性能好等优点,比钢筋混凝土盖板涵更适合用于青藏公路这样的寒区工程[2]。2001年,季文玉进行了小直径金属波纹管涵洞在青藏铁路的受力行为理论分析与试验研究,测试了回填土压力和波纹管应力、变形的变化[3]。2005年李祝龙对波纹钢板涵洞力学性能进行了现场试验研究,得到以下结论:当填土高度为0.3 m时,钢波纹管涵洞的管顶附近在施工活载的作用下,存在较大的应力集中现象。钢波纹管涵的管顶、管侧沿着波形方向呈现出不同的应力变化趋势,波峰和波谷处以及内外侧,切向和轴向应力应变呈现出管顶与管侧相反的情况[4]。2008年,王艳丽对钢波纹管涵洞进行了薄壳效应的研究,从旋转对称壳基本理论着手,针对工程现场采用过的反开槽回填法施工,建立了有限元力学模型,结果表明模型得到的计算结果和现场实测值拟合良好,说明钢波纹结构是一种典型的旋转壳,可以用薄壳中旋转对称壳理论分析,该方法是可行的[5]。2013年张闻达对波纹钢板桥涵的分类与选形进行了详细的介绍,并利用有限元模型来研究各参数对结构性能影响的规律,从而确定波纹钢板桥涵合理选形原则。建议设计人员首先考虑圆形截面是否满足要求,如果其净空不满足要求,才会按顺序考虑管拱形、横向椭圆形、开口拱形等截面形式,如果跨度大,可以考虑采用加强的截面[6]。2014年,杨明辉基于原位观测试验与理论研究,对高填方段波纹圆管涵的涵顶垂直土压力的分布特征与变化规律进行了探讨。结果表明,高填方段管涵顶部存在土拱效应,规范的土柱法计算土压力值误差较大,偏于保守;土体重度对管涵垂直土压力数值影响较大,而内摩擦角及黏聚力的影响较小[7]。
国外对其他线形的研究已经展开。2008年,Halil Sezen对4座建成的管拱形结构波纹钢管涵进行了静载和动载试验。结果表明管涵的力学性能主要受填土高度的影响;在对称荷载作用下,管拱的变形在垂直平面内也基本对称;结构在最大静荷载作用下的变形比相同条件下动荷载作用下的变形要大10%~20%[8]。2009年,美国俄亥俄州交通局(ODOT)对其境内的39座现役波纹钢板管拱形、圆形管涵和低弧拱形式分别进行了静力试验和跑车试验。测试结果表明:结构在汽车荷载作用下的变形随填土高度的增加呈现出非线性减小的趋势;跑车过程中结构的变形比静荷载作用下的变形小10%~20%;拱顶处的应变类似梁的弯曲,波峰以压为主,波谷以拉为主[9]。2012年,Damian Beben教授对两座现役并排的管拱形铁路波纹钢板涵洞在工作荷载下的位移、应变和加速度进行了监测。监测结果显示最大位移和应变分别发生在管顶和管侧1/4位置[10]。2013年,Kyong Y. Yeau等研究了回填高度、荷载、管涵尺寸、形状等因素对管拱形覆土波纹钢板管涵性能的影响,分别用二维和三维有限元模型与实测数值进行对比分析。结果表明二维有限元模型的计算位移要大于实测位移值,轴力则相接近;三维有限元模型的计算位移和轴力与实测值均接近;影响管拱形覆土波纹钢板管涵受力性能的因素包括回填高度、管涵尺寸、管涵钢板厚度、回填土的弹性模量及土的其他性质[11]。
目前国内对非圆形截面形式的波纹钢管涵的研究还基本没有展开,本文拟采用有限元方法,通过建立同跨径的圆形截面和管拱形截面波纹钢管涵的二维平面应变模型,分析其在施工过程中随填土高度的增加管涵变形、应力和土压力的变化情况,通过对比得出两种截面形式的管涵在变形和内力方面的一般性规律,为以后波纹钢管涵的设计和施工提供一定的指导。
1 有限元模型建立及验证 1.1 二维平面应变模型建立平面模型以其建模简便、运行速度快的优点成为科研工作者和设计人员进行结构研究和设计的首选方案。对于波纹钢管涵这种小跨径结构,由于管涵纵向长度远大于管涵直径,可按照钢板管涵根据抗弯刚度等效的原则,沿纵向取单位长度的管涵简化为平面应变问题,采用二维平面应变模型来进行计算。通过将波纹钢管结构三维模型与二维模型计算结果进行对比,发现两者弯矩基本吻合,轴力存在些许不同,误差在7%左右,因此可以用平面模型代替波纹钢板三维模型[12]。本文比较不同线形管涵受力特点时,使用二维有限元模型计算可以满足精度要求。
有限元模型中采用beam3二维梁单元来模拟波纹钢板,可承受拉、压、弯作用,波纹钢板截面积和惯性矩均为单位长度的截面积和惯性矩,由所选用的波纹钢板型号计算确定[13]。采用plane82二维平板单元来模拟土体,该单元可以适应不规则形状而减少损失精度,具有塑性、蠕变、辐射膨胀、应力刚度、大变形及大应变的能力。采用targe169和contac172单元来模拟管涵和土体之间的接触问题。覆土波纹钢桥涵结构的存在对3倍跨径以外土体的土压力分布几乎不存在影响,因此在建立有限元模型时,管涵两侧的土体应分别取3倍的跨径[14]。管涵土体的左右边界采用可竖向滑移的滑动支座,管涵土体的下边界采用固定铰支座。
按照以上的几点建模原则,根据一个实际覆土波纹圆管涵试验模型[15]的结构和材料参数建立二维平面应变有限元模型,模拟整个回填土施工过程。模型中圆管涵的直径为1.2 m,波纹钢板的波形为200 mm×55 mm×3.5 mm,单位长度面积为4.08 mm2/mm,单位长度惯性矩为1 437.08 mm4/mm,波纹钢板的弹性模量2.06×105 MPa,密度7 850 kg/m3,泊松比取0.3;填土至管顶以上5.1 m,管下底层土弹性模量取50 MPa,回填土弹性模量取20 MPa,土的密度为1 900 kg/m3,土的泊松比为0.25,土内摩擦角取30°。
建立有限元模型的具体过程如下:(1)定义材料特性,建立几何模型; (2)对不同单元划分网格;(3)建立接触对,生成接触单元,并设置接触单元实常数;(4)施加约束,土体两侧约束横向位移,土体底面约束横向和竖向位移;(5)加载并定义求解选项,进行求解,输出结果。
建模过程如图 1所示。
|
| 图 1 有限元建模过程示意 Fig. 1 Process of FE modelling |
以试验模型施工回填过程中管两侧水平距离最大处的水平相对位移、管顶与管底的竖向相对位移的实测结果与有限元模型计算结果对比来验证模型的有效性。相对位移采用数显收敛计进行测试,每层填土结束时使用数显收敛计进行一次测量并记录。图 2给出了圆管涵水平位移和竖直位移实测值和模型计算结果的比较。
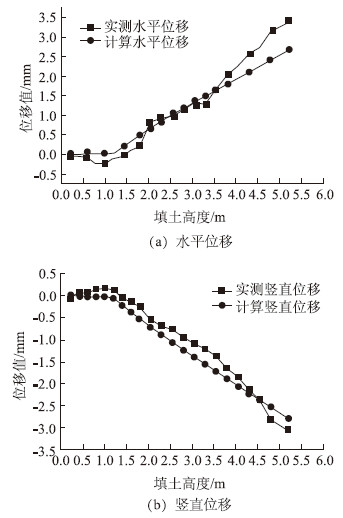
|
| 图 2 圆管涵模型施工过程位移比较 Fig. 2 Comparison of displacements of circular pipe culvert model during construction |
图 2中位移值正值为测点位移方向向外(外凸),负值表示测点位移方向向内(内凹)。从图 2(a)中可以看出,水平位移的实测值和模型计算值的变化趋势基本相同,并且数值相差不大。当填土高度低于1.2 m时,填土在拱顶以下,实测值和计算值都随填土高度的增加而减小;当填土高度超过1.2 m,填土作用于拱顶以上,实测值和计算值都随填土高度的增加而增加。从图 2(b)中可以看出,竖直位移的实测值和模型计算的理论值的变化趋势基本相同,并且数值也相差不大。当填土高度低于1.2 m时,实测值和计算值都随填土高度的增加而增加;当填土高度大于1.2 m时,实测值和计算值都随填土高度的增加而减小。考虑由于施工过程中施工机械的影响以及操作人员使用数显收敛计读数时存在的人为误差,实测曲线没有计算曲线光滑。总结变形规律,可以看出在回填土填到管顶之前,管涵随着填土高度的增加逐渐向两侧土体挤压圆管,圆管逐渐上拱;当回填土高过管顶之后,由于土体重力作用于管顶,上拱值逐渐回落。通过以上对试验模型施工过程中位移的实测值和模型计算结果的对比,说明有限元模型可以有效地模拟施工过程中结构的受力变形情况,证明了有限元模型的有效性,可以用来做进一步的分析。
2 有限元数值分析为了对比研究圆形截面和管拱形截面波纹钢管涵在施工过程中力学性能的一般规律,本文选取跨径4 m的圆管涵和跨径4 m、矢高2.4 m的管拱形桥涵[16]。波纹钢板的波形采用200 mm×55 mm×6 mm,单位长度面积为6.998 mm2/mm,单位长度惯性矩为2 464.187 mm4/mm,其他参数同上。运用上文的建模方法分别建立二维有限元模型进行计算分析。模型中按照30 cm一层进行回填土施工过程模拟,按照层数模拟均回填至管顶以上1.1 m左右结束。两种截面有限元模型如图 3所示。
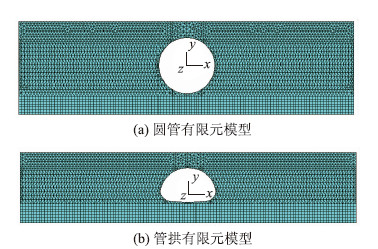
|
| 图 3 有限元模型 Fig. 3 Finite element models |
对4 m跨径圆管和4 m跨径管拱施工过程中管两侧水平距离最大处的水平相对位移有限元计算值进行对比,如图 4所示。
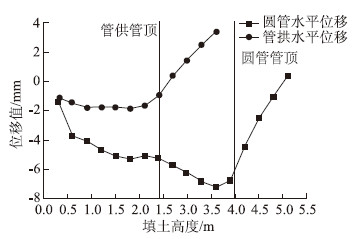
|
| 图 4 施工过程中水平位移对比 Fig. 4 Comparison of horizontal displacements during construction |
从图 4可以看出,圆管在填土高度低于4 m时(管顶附近),水平位移值为负值,且随填土高度的增加而逐渐减小,填土高度为3.6 m时,水平位移达到最小值-7.26 mm。圆管在填土高度大于4 m时,水平位移随填土高度的增加而逐渐增加,填土高度为5.1 m时水平位移值由负值变为正值,说明此时圆管水平方向由内凹变为外凸。管拱在填土高度低于2.4 m时(管顶附近),水平位移值为负值,且随填土高度的增加而逐渐减小,填土高度为1.8 m时,水平位移达到最小值-1.86 mm。管拱在填土高度大于2.4 m时,水平位移值为正值,且随填土高度的增加而逐渐增加,说明此时管拱水平方向由内凹变为外凸。随填土高度的增加,两管水平位移变化趋势基本相同,但圆管的内凹值远大于管拱,填土到管顶1.1 m时管拱的外凸值大于圆管涵。
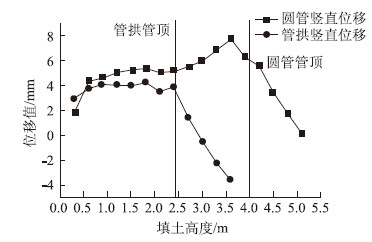
对4 m跨径圆管和4 m跨径管拱施工过程中管顶与管底的相对竖直位移有限元计算值进行对比,如图 5所示。
|
| 图 5 施工过程中竖直位移对比 Fig. 5 Comparison of vertical displacements during construction |
从图 5可以看出,圆管在填土高度低于4 m时(管顶附近),竖直位移值为正值,且随填土高度的增加而逐渐增加,填土高度为3.6 m时,竖直位移达到最大值7.71 mm。圆管在填土高度大于4 m时,竖直位移值为正值,且随填土高度的增加而逐渐减小,说明圆管竖直方向上拱逐渐回落,填土结束时依然处于上拱状态。管拱在填土高度低于2.4 m时(管顶附近),竖直位移值为正值,且随填土高度的增加而逐渐增加,填土高度为1.8 m时,竖直位移达到最大值4.25 mm。管拱在填土高度大于2.4 m时,竖直位移值由正值逐渐变为负值,说明竖直方向管拱由外凸逐渐变为内凹。随填土高度的增加,两管有限元计算值变化趋势基本相同,圆管的竖直位移大于管拱的竖直位移。这说明随填土高度的增加,两管竖向位移变化趋势基本相同,但圆管涵的上拱值远大于管拱,但填土到管顶1.1 m时管拱的内凹值大于圆管涵。
因此,管拱形管涵在填土达到管顶之前受填土的影响较小,而填土超过管顶后影响较大,这是由于其形状特点决定的,由于其矢跨比较小,横向水平刚度较大,但当土压力作用于顶部时受荷面积相对较大,对其受力性能影响也较大,这从后面管涵土压力和应力的分析中也可以看出。
2.2 管涵土压力对比研究对4 m跨径圆管和4 m跨径管拱施工过程中管两侧水平距离最大处的水平土压力有限元计算值与按土柱法计算的水平土压力结果进行对比,如图 6所示。

|
| 图 6 施工过程中管侧水平土压力比较 Fig. 6 Comparison of horizontal earth pressures on pipe side during construction |
从图 6中可以看出,圆管涵在填土高度低于4 m时(管顶附近),有限元计算值土柱法计算值基本相同,在填土高度大于4 m时,有限元计算值明显大于土柱法计算值,且随填土高度的增加数值上的差距越来越大。管拱在填土高度低于2.4 m时(管顶附近),有限元计算值与土柱法计算值基本相同,在填土高度大于2.4 m时,有限元计算值明显大于土柱法计算值,且随填土高度的增加数值上的差距越来越大。当拱上填土高度为1.1 m时管拱的水平土压力大于圆管涵。
这与上面位移的分析是相应的,由于填土高于管顶后,两管涵都有管顶下挠、管侧内凹的趋势,使得管侧水平土压力迅速增加,而管拱两侧相对水平位移更大,因此水平土压力增长更明显。
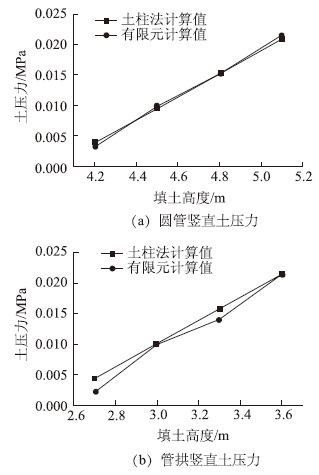
对4 m跨径圆管和4 m跨径管拱施工过程中管顶处的竖直土压力有限元计算值与按土柱法计算的竖向土压力结果进行对比,如图 7所示。
|
| 图 7 施工过程中竖直土压力比较 Fig. 7 Comparison of vertical earth pressures during construction |
从图 7中可以看出,两管有限元计算值与土柱法计算值基本相同。但由于管拱竖直方向下挠大于圆管涵,对土起到一定的卸载作用,因此竖向土压力有限元计算值略小于土柱法计算值。
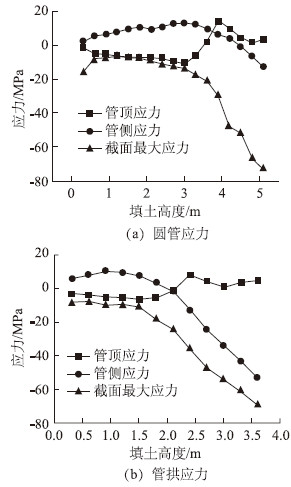
2.3 管涵应力对比研究对4 m跨径圆管和4 m跨径管拱各层填土作用下的应力变化进行计算分析,选择管顶处、管两侧水平距离最大处的内侧应力值以及截面最大应力值进行对比,正值表示拉应力,负值表示压应力。对比结果如图 8所示。
|
| 图 8 施工过程中应力比较 Fig. 8 Comparison of stresses during construction |
从图 8中可以看出,圆管涵和管拱的管两侧水平距离最大处的应力在填土至管顶之前为正值,表明受拉,且随填土高度的增加而增加,当填土超过管顶后,随填土高度的增加逐渐变为负值,表明受压;而两管的管顶应力在填土至管顶之前为负值,表明受压,在填土超过管顶后逐渐变为正值,表明受拉,之后又有向受压变化的趋势。这与上面位移的分析是相应的,由于填土低于管顶时,两管涵都有管顶上拱,管中内凹的趋势,因此管顶内侧应力为压应力,管两侧内侧应力为拉应力;当填土高于管顶后,两管涵逐渐管顶下挠、管中外凸,因此管顶内侧应力为拉应力,管两侧内侧应力为压应力;随着管顶以上填土增加,管涵各点逐步全部趋于受压,验证了“环向压力理论”[14]。圆管和管拱施工过程中应力变化规律虽然基本一致,但数值是有一定差别的,这主要是因为二者虽然跨径相同,但矢高比不同,当超过管顶后管拱的应力变化更明显,这与前述的变形规律对比也是一致的。
两管涵最大应力变化趋势相同,当涵管顶以上填土1.1 m左右时截面最大应力对比如表 1所示。
| 截面形式 | 截面最大应力/MPa | 最大应力出现位置 |
| 圆管 | -73.06 | 管中略靠下处 |
| 管拱 | -69.23 | 管两侧水平距离最大处 |
由表 1可以看出,二者的最大应力数值和出现的位置略有差别。数值的差别在相关规范中也有体现,规范中[14, 17]用起拱系数Af考虑结构在回填材料挤压下产生上拱而使拱上土体荷载增大的效应,该系数的取值与结构有效跨度Dh和有效矢高Dv之比以及填土高度相关。通过规范的相关表格可得管上填土1.1 m左右时,本文所选圆管的Af=1.27,管拱的Af=1.20,因此圆管最大应力略大,说明本文计算结果与相关规范也是一致的。
3 结论通过以上研究分析可得:
(1)本文采用的二维平面有限元模型中的单元选取、结构简化和施工模拟等建模思想是正确的,模型可以有效地预测施工过程中结构的变形情况。
(2)圆管和管拱变形趋势基本一致,在回填土填到管顶之前,管涵随着填土高度的增加逐渐上拱,当回填土超过管顶之后,拱顶逐渐回落,恢复初始状态后而逐渐下挠。管拱在施工填土超过管顶后的变形变化比圆管显著。
(3)施工过程中圆管和管拱土压力变化规律基本一致,由于管拱填土超过拱顶后的下挠较圆管明显,其竖直土压力略小。
(4)圆管和管拱施工过程中应力变化规律基本一致,填土超过管顶后,管拱应力变化较大,管顶以上填土1.1 m左右时,由于起拱效应的影响,圆管截面最大应力略大于管拱截面最大应力。
| [1] | 杨猛, 陈宝永, 沈翰斌, 等.公路应用波纹钢结构涵洞的可行性探讨[J].黑龙江交通科技, 1999, 15(2):51-53. YANG Meng, CHEN Bao-yong, SHEN Han-bin, et al. Discussion of Feasibility of Corrugated Steel Culvert in Highway Application[J]. Communications Science and Technology Heilongjiang, 1999, 15(2):51-53. |
| [2] | 李祝龙, 章金钊.高原多年冻土地区波纹管涵应用技术研究[J].公路, 2000, 45(2):28-31. LI Zhu-long, ZHANG Jin-zhao. Research on Applied Technology of Corrugated Steel Pipe Culvert in Plateau Permafrost Region[J]. Highway, 2000, 45(2):28-31. |
| [3] | 季文玉.金属波纹管涵洞受力行为理论分析与试验研究[D].北京:北京交通大学, 2004. JI Wen-yu. Theoretical Analysis and Experimental Study on Stress Behavior of Corrugated Steel Pipe Culvert[D].Beijing:Beijing Jiaotong University, 2004. |
| [4] | 李祝龙, 刘百来, 李自武.钢波纹管涵洞力学性能现场试验研究[J].公路交通科技, 2006, 23(3):79-82. LI Zhu-long, LIU Bai-lai, LI Zi-wu. Field Mechanical Performance Test of Corrugated Steel Culvert[J]. Journal of Highway and Transportation Research and Development, 2006, 23(3):79-82. |
| [5] | 王艳丽, 李祝龙, 吴大中.钢波纹管涵洞的薄壳效应[J].公路交通科技, 2008, 25(5):86-90. WANG Yan-li, LI Zhu-long, WU Da-zhong. Thin Shell Effect of Corrugated Steel Culvert Performance[J]. Journal of Highway and Transportation Research and Development, 2008, 25(5):86-90. |
| [6] | 张闻达.波纹钢板小桥合理形式研究[D].西安:长安大学, 2013. ZHANG Wen-da. Research on Reasonable Structure Form of Corrugated Steel Bridge[D].Xi'an:Chang'an University, 2013. |
| [7] | 杨明辉, 方天云, 赵明华, 等.高填方段波纹管涵垂直土压力试验及计算[J].公路交通科技, 2014, 31(4):33-38. YANG Ming-hui, FANG Tian-yun, ZHAO Ming-hua, et al. Test and Calculation of Vertical Earth Pressure on Corrugated Pipe Culvert Under High Embankment[J]. Journal of Highway and Transportation Research and Development, 2014, 31(4):33-38. |
| [8] | SEZEN H, YEAU K Y, FOX P J. In-situ Load Testing of Corrugated Steel Pipe-arch Culverts[J]. |
| [9] | YEAU K Y, SEZEN H, FOX P J. Load Performance of in Situ Corrugated Steel Highway Culverts[J]. |
| [10] | BEBEN D. Corrugated Steel Plate Culvert Response to Service Train Loads[J]. Journal of Performance of Constructed Facilities, 2012, 28(2):376-390. |
| [11] | YEAU K Y, SEZEN H, FOX P J. Simulation of Behavior of In-service Metal Culverts[J]. Journal of Pipeline Systems Engineering and Practice, 2013, 5(2):1-8. |
| [12] | 彭贤明. 钢波纹板桥梁结构数值分析[D].广州:华南理工大学, 2012. PENG Xian-ming. Numerical Analysis of Steel Corrugated Plate Bridge Structure[D].Guangzhou:South China University of Technology, 2012. |
| [13] | 刘保东, 尹航, 冯芝茂, 等.基于土-钢共同作用模型的覆土波纹钢板拱桥施工过程受力分析[J].北京交通大学学报:自然科学版, 2009, 35(4):65-68. LIU Bao-dong, YIN Hang, FENG Zhi-mao, et al. Mechanics Behavior of Buried Corrugated Steel Arch Bridge Based on Soil-steel Interaction Mode During Construction[J]. Journal of Beijing Jiaotong University:Natural Science Edition, 2009, 35(4):65-68. |
| [14] | CAN/CSA-S6-00, Canadian Highway Bridge Design Code[S]. |
| [15] | 王振.覆土波纹钢管涵刚柔性的对比试验研究[D].北京:北京交通大学, 2012. WANG Zhen. Comparative Experimental Study on Rigidity and Flexibility of Buried Corrugated Steel Pipe Culverts[D].Beijing:Beijing Jiaotong University, 2012. |
| [16] | AS/NZS 2041, Buried Corrugated Metal Structures[S]. |
| [17] | DB 15/T 654-2013, 公路波纹钢管(板)桥涵设计与施工规范[S]. DB 15/T 654-2013, Specification for Design and Construction of Corrugated Steel Pipe and Plate for Highway Bridges and Culverts[S]. |
 2015, Vol. 31
2015, Vol. 31
