扩展功能
文章信息
- 李斐然
- LI Fei-ran
- 临时支点对“桥上桥”承载能力的影响
- Influence of Bearing Capacity of Bridge on Bridge with Temporary Supports
- 公路交通科技, 2015, Vol. 31 (10): 62-67
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (10): 62-67
- 10.3969/j.issn.1002-0268.2015.10.011
-
文章历史
- 收稿日期: 2014-10-21
“桥上桥”[1, 2]技术在目前众多旧桥加固方法中是速度最快、施工最简便、投资最少的一种方法,特别适合于大型设备公路运输中对承载力不足的低等级或破损桥梁的临时加固,也适合于铁路建设中重型设备运输、重型施工车辆通过低等级或破损桥梁的临时加固[3, 4, 5]。“桥上桥”的技术原理是:对于承载力不足的桥梁,通过在原有桥梁上架设新的桥梁结构来承受车辆荷载,确保车辆通行前后不对原桥产生损害。传统的“桥上桥”加固方法是直接利用新桥来承受车辆荷载,这种方法没有利用原桥的剩余承载力,造成新桥设计尺寸偏大,加固代价高,若在“桥上桥”加固时在原桥与新桥梁结构之间设置一定的荷载传递方式,让原桥分担一部分车辆荷载,既能降低新桥的造价,又能提高“桥上桥”结构整体的承载能力极限值。原桥与新建桥梁结构之间最便捷的荷载传递模式是通过临时支点传递,临时支点减小了新建桥梁的活载跨径,将部分活载传递给原桥,这种方法造价低,施工方便,可根据实际情况随时调整。
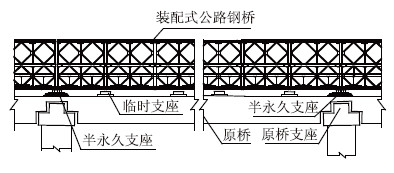
某桥全长406.1 m,桥宽24 m,其中行车道宽21 m,两侧各1.5 m人行道。上部构造为2联5孔40 m部分预应力混凝土简支组合箱梁桥,桥台和5号墩分别设置HZF-100和HZF-180型伸缩装置,其余桥墩顶箱梁设置桥面连续板,下部构造采用单排四柱式墩台,钻孔灌注桩基础。设计荷载:汽-超20,挂-120。某大件运输超限车辆途经该桥,车辆总质量为696 t,根据桥梁在超限车辆荷载作用下的检算结果,需对该大桥采用“桥上桥”[2, 6, 7]的承载力提高方案。经分析,单独采用装配式公路钢桥[8]无法承担该车辆荷载,需要原桥分段部分活载[9],设置临时支座后,通过装配式公路钢桥和原桥共同承载的办法可提高“桥上桥”。这种新结构整体承受超重荷载的能力,见图 1。但如何确定临时支座的设置位置,如何通过临时支座确定原桥和装配式公路钢桥的荷载分担比例是需要解决的两大问题。本文将基于理论分析和有限元相结合的分析方法,研究提高“桥上桥”整体承载能力的方法。
|
| 图 1 包含临时支点的“桥上桥”示意图 Fig. 1 Bridge on bridge with temporary supports |
临时支点起着承上启下的作用,临时支点一方面要尽可能地减小装配式公路钢桥的内力,另一方面要避免传递到原桥上的局部荷载和整体内力过大,因此临时支点的数量和位置均存在一个合理区间。
根据常用的几种数列形式,拟定支座位置布置可采用多种形式:等间距布置、黄金分割点布置、斐波那契等整数数列模式布置。由于装配式公路钢桥为模数式的结构,支座间距为3 m模数的整数倍,考虑实际中的易操作性,避免复杂的支点布置形式,仅考虑等间距布置方式。
1.1 支座数量的确定在支座数量确定前做3条假定:(1) 临时支座无初始间隙;(2) 新桥与原桥均处于线弹性状态;(3) 新桥与原桥均为简支受力状态。
第1步:假定装配式公路钢桥的抗弯承载力为Mu1,抗剪承载力为Qu1,为简化计算,公路Ⅰ级中的集中力P转换为均布荷载,公路Ⅰ级的等效均布荷载为q,集中力和均布力产生效应的差别由系数k进行调整,每个临时支点提供的有效支撑力为Pi(i=1,2,…,n),每个临时支点距离左支点距离为lli,距离右支点距离为lrj,那么可以得到:

梁上其任意一点(距离梁左支点距离为Di)的弯矩为:
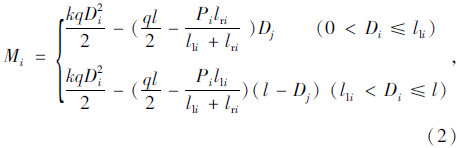
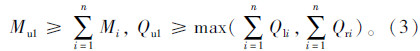
第2步:假定原桥的剩余抗弯承载力为Mu2,剩余抗剪承载力为Qu2,跨间临时支点数量为m,每个临时支点传递下来的荷载为Pi(i=1,2,…,m),每个临时支点距离左支点距离为llj,距离右支点距离为lrj那么可以得到对于荷载Pj,两侧支点位置的剪力为:
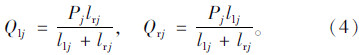
梁上其任意一点(距离梁左支点距离为Dj)的弯矩为:
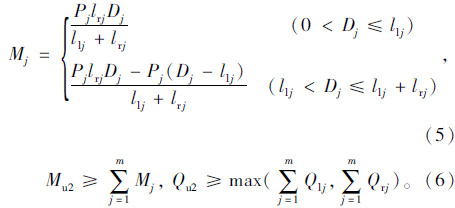
第3步:根据第1步确定新桥能承担的荷载所需的最小支点数量n,根据第2步确定原桥能承担的荷载所需的最小支点数量m,取两个数值的并集,即可得到支点数量范围,当两者没有并集时应进一步提高新桥的承载力。
1.2 对实桥的计算分析对前述桥梁采用前面的方法确定支座数量,为了简化计算过程,假定各临时支点传递下来的集中荷载Pi为相同数值P,计算过程如下:
(1)装配式公路钢桥需要的临时支座数量
装配式公路钢桥双层三排加强型321桁架的抗弯承载力为9 618.8 kN·m,抗剪承载力为698.9 kN,40 m跨径下,弯矩能承受的均布力为48 kN/m,剪力能承受的均布力为35 kN/m,大件运输的车辆荷载为64.4 kN/m,因此装配式公路钢桥最大能承担大件运输车辆荷载的53%。21 m跨径下,弯矩能承受的均布力为174.5 kN/m,剪力能承受的均布力为66.6 kN/m,双层三排加强型321桁架此时可保证自身的结构安全,因此对于依托工程中的大件运输车辆,需要的最小支点数量n为1个。
(2)原桥需要的临时支座数量
原桥的抗弯承载力为13 400 kN·m,抗剪承载力为2 952 kN,恒载下跨中下缘压应力储备为4.34 MPa。对于原桥需要确保桥梁状态满足正常使用极限状态,从而避免车辆过桥对原桥损伤,根据计算40 m跨径下正常使用极限状态能承受的最大均布力为25 kN/m,相当于原桥最大能承担大件运输车辆荷载的40%。
由于原桥承受的为装配式公路钢桥通过临时支座传递下来的集中力,根据集中力产生的弯矩与均布荷载产生的弯矩效应差别可以得到,一个支点时不考虑间隙原桥能承受25%的大件运输车辆荷载;两个支点时不考虑间隙原桥能承受37.5%;三支点时不考虑间隙原桥能承受45%;四支点时不考虑间隙原桥能承受50%。对于依托工程中的大件运输车辆,需要的最小m为3个。
(3) 根据前面两步计算过程,确定临时支点数量最小为3,由于原桥运营时间较久,存在一定的病害,并且支座预留间隙可调整支座力的分布,为了保证临时支点的荷载能均匀传递到原桥上,确定装配式公路钢桥的合理临时支点数量为3~5个。
2 考虑间隙单元的非线性有限元分析接触非线性问题是指由于接触边界的不确定导致整个问题解的非线性,间隙元属于接触非线性的一种,结构的有限元计算模型中包含了间隙元后,由于边界条件的不确定性,在加载过程中不能预测间隙是扩大还是减小,因此它的计算过程是非线性的。
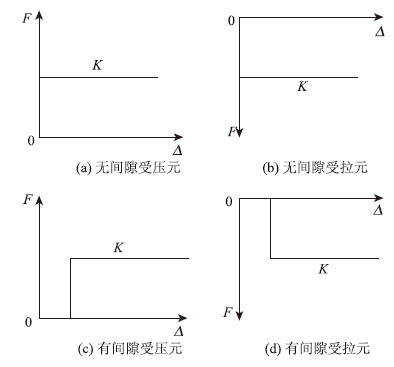
2.1 间隙元介绍间隙元[10]由两个节点定义,两个节点之间的长度一般定义为间隙量,间隙元根据用途可为压间隙元和拉间隙元,压间隙元是在间隙为零时(即变形后节点间距为零或允许值)才起作用,而拉间隙元在拉开后有间隙才起作用。间隙元常在桥梁工程用于模拟支架施工的桥梁结构,间隙元作为结构与基础或支撑之间的弹性连结,模拟支架与结构的接触特性,间隙单元的刚度由实际弹性支承计算确定。在使用间隙元的有限元分析中,材料性质仍然假定为线弹性、小变形范围内。单元的几何刚度、非线性应变及滑动引起的摩擦力不予考虑,加载和卸载不会耗散能量,结构的应变和应力完全由最后的变形决定,而与加载路径无关。常用的间隙元有:无间隙受压元、有间隙受压元、无间隙受拉元和有间隙受拉元[11]。4种间隙元的刚度特性曲线如图 2所示。
|
| 图 2 四种间隙元的刚度曲线 Fig. 2 Stiffness curves of 4 gap elements |
活载计算包括两种方法,一种是目前有限元程序中常用的影响线计算加载法,通过集中荷载计算出影响线,然后依据动态规划法计算出影响线加载的最大值[12];一种是按照穷举法进行车辆位置布置得到最大值的方法,而穷举法计算量大在实际中已很少应用。间隙单元造成边界条件的非线性,桥梁叠加原理的条件不再成立,不能用影响线加载法进行结构内力、位移的包络图计算。
对于大件运输车辆,自身的特点为车辆荷载固定轴载、固定轴间距和固定行车位置,车辆行驶过程中只有单辆车,不需要按照常规活载计算中考虑偏载、车辆布置方式等因素的影响,活载计算相对简单,为此可按照车辆从左至右行驶的方式,采用前面的非线性分析方法,逐点施加荷载,这样计算过程中每个步骤均可考虑支座的间隙单元影响,可以精确地得到各个节点和单元在各种荷载作用下的最大值响应。
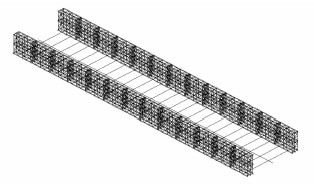
2.3 间隙单元初始间隙量的确定图 3为考虑间隙单元的有限元计算模型,除了间隙单元的位置会影响计算结果外,间隙量也同样对计算结果影响较大,间隙量过小原桥承受的荷载将增加,间隙量过大则装配式公路钢桥承受的荷载比例将增加,因此合适的间隙量是调整原桥与装配式公路钢桥承担荷载比例的重要因素。
|
| 图 3 考虑间隙单元的有限元计算模型 Fig. 3 FE model with gap elements |
间隙模式1(等间距模式):各临时支点间隙量按照相同数值取值;
间隙模式2(挠曲线模式):各临时支点间隙量根据装配式公路钢桥的恒载挠度曲线等比例取值。
3 “桥上桥”结构受力分析根据某大桥的“桥上桥”加固方案,分别按照3~5个等间距的临时支点进行活载非线性状态的计算,支座间隙由前述方式确定。
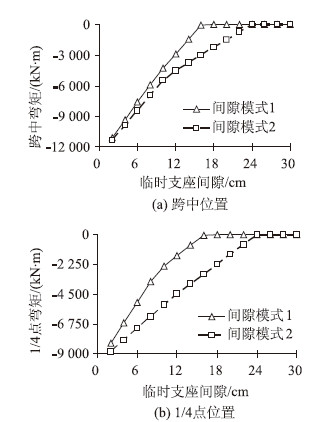
3.1 三个临时支点采用三个临时支点,支座间隙按照2~24 cm进行布置,采用不同间隙模式得到的临时支座间隙与跨中点活载弯矩关系图如图 4(a)所示,临时支座间隙与1/4点活载弯矩关系图如图 4(b)所示。从图中可以看出两种模式下支座间隙与最大弯矩基本呈线性变化。采用等支座间隙模式时支座间隙在16 cm 时最大弯矩达到最小,数值上接近0,可认为此时临时支座失去作用;采用间隙模式2,即挠曲线模式时支座间隙在24 mm时最大弯矩减小到0。两种模式下间隙模式1斜率偏大,间隙模式2斜率偏小,间隙模式2较间隙模式1对于临时支座间隙的误差不敏感,间隙模式2更利于实际工程应用。
|
| 图 4 三个临时支座时间隙与活载弯矩关系图 Fig. 4 Curves of gap vs. live load bending moment of structure with 3 temporary supports |
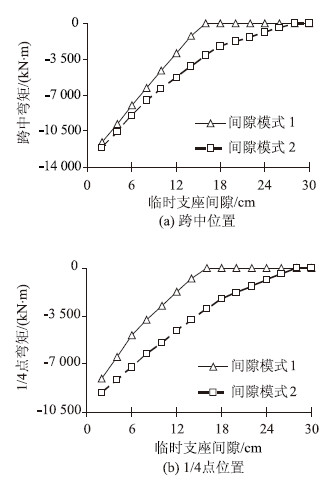
采用四个临时支点,支座间隙按照2~28 cm进行布置,采用不同间隙模式得到的计算结构如图 5所示,从图中可以看出支座间隙模式1即等支座间隙模式时与最大弯矩基本呈线性变化,间隙模式2即挠曲线间隙模式时与最大弯矩呈抛物线形变化。采用支座间隙1在16 cm时最大弯矩达到最小,数值上接近0,可认为此时对主梁基本无影响;采用挠曲线模式时支座间隙在28 mm时最大弯矩减小到0,两种模式下间隙模式1斜率大,间隙模式2斜率小,间隙模式2较间隙模式1对于临时支座间隙的误差不敏感,对于四个临时支点,间隙模式2与三个临时支点一样更利于实际工程应用。
|
| 图 5 四个临时支座时间隙与活载弯矩关系图 Fig. 5 Curves of gap vs. live load bending moment of structure with 4 temporary supports |
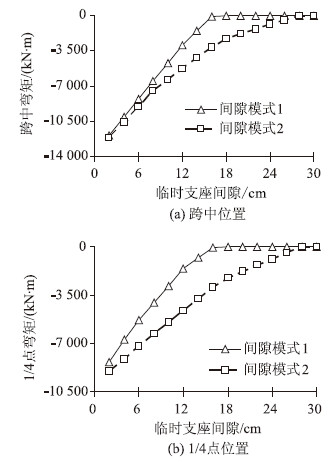
采用五个临时支点,支座间隙按照2~28 cm进行布置,采用不同间隙模式得到的计算结构如图 6所示,从图中可以看出支座间隙模式1与最大弯矩基本呈线性变化,间隙模式2与最大弯矩呈抛物线形变化。采用等支座间隙模式时支座间隙在16 cm时最大弯矩达到最小,数值上接近0,可认为此时对主梁基本无影响;采用挠曲线模式时支座间隙早28 mm 时最大弯矩减小到0,两种模式下间隙模式1斜率大,间隙模式2斜率小,五个临时支点下在模式2时,弯矩随着支点间隙的增大变化更为平缓,使得弯矩对于支点间隙变化更不显著。
|
| 图 6 五个临时支座时间隙与活载弯矩关系图 Fig. 6 Curves of gap vs. live load bending moment of structure with 5 temporary supports |
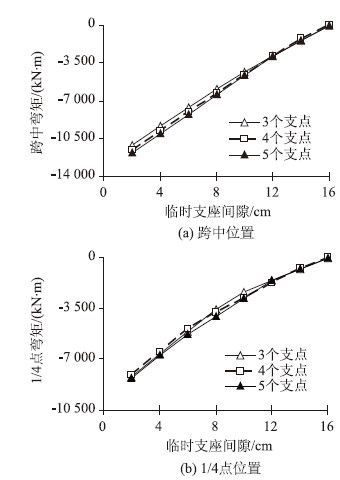
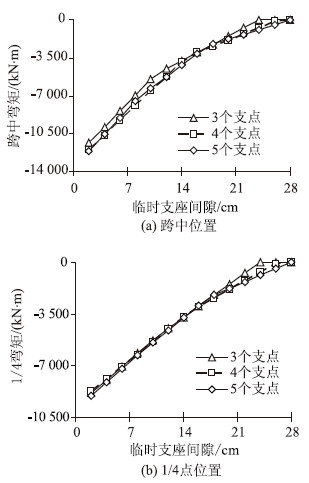
图 7为间隙模式1下不同支点数量与原桥活载弯矩关系图,图 8为间隙模式2下不同支点数量与原桥活载弯矩关系图。从图 7中可以看到,模式1下不同支点数量对于原桥跨中弯矩影响并不大,基本均呈线性变化,间隙大小与原桥弯矩直接相关,可认为支点数量的选择重要性小于支点间隙。从图 8中可以看到,模式2下不同支点数量同样对原桥跨中弯矩影响不大,但弯矩与支点间隙呈抛物线变化,支点数量越多曲线在接近零弯矩时变化也更趋于平缓。
|
| 图 7 间隙模式1下不同支点数量与活载弯矩关系图 Fig. 7 Curves of support number vs. live load bending moment of structure under gap mode 1 |
|
| 图 8 间隙模式2下不同支点数量与活载弯矩关系图 Fig. 8 Curves of support number vs. live load bending moment of structure under gap mode 2 |
本章对“桥上桥”提载方式中的临时支点位置、临时支点数量、临时支点间隙进行了研究,并通过考虑间隙单元的有限元法对装配式公路钢桥的性能进行了实桥分析,得到的结论如下:
(1)支点数量的选择需要平衡装配式公路钢桥和原桥的承载力,以使二者同时达到允许承载力为原则确定支点数量。
(2)各临时支点间隙量按照相同数值的模式取值时,不同支点数量对于原桥跨中弯矩影响并不大,基本均呈线性变化,但间隙大小与原桥弯矩直接相关。
(3)各个临时支点的初始间隙量根据装配式公路钢桥的恒载挠曲线比值关系模式取值时,不同支点数量同样对原桥跨中弯矩影响不大,但与等间隙模式不同的是,原桥最大弯矩与支点间隙呈类抛物线形状变化,支点数量越多曲线在接近零弯矩时变化越平缓,该模式对于误差的敏感性低,更利于实际工程采用。
(4)临时支点间隙对原桥的内力影响较大,临时支点数量和位置对原桥的内力影响较小,在实际应用时建议采用便于施工的临时支点布置方式,通过控制支点间隙控制原桥承载水平。
| [1] | 蒙云, 戚志河. 用"桥上桥"解决323 t重载通过16 m 梁桥的设计与实践[J]. 重庆交通学院学报, 2006, 25(增1):21-23, 31. MENG Yun, QI Zhi-he. Design and Practice of Solving 323 ton Heavy-cargo by Temporary Steel Bridge to Pass Bridge of Span 16 m[J]. Journal of Chongqing Jiaotong University, 2006, 25(S1):21-23, 31. |
| [2] | 刘尧, 叶贵如, 张治成. 桥上桥在大件运输中的应用研究[J]. 武汉理工大学学报:交通科学与工程版, 2008, 32(1):176-179. LIU Yao, YE Gui-ru, ZHANG Zhi-cheng. Method "bridge on the bridge" Used in the Massive Product Transportation[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition, 2008, 32(1):176-179. |
| [3] | 张永宝, 胡振文. 关于提高"桥上桥"技术水平的探讨[J]. 石家庄铁道学院学报, 1997, 10(2):75-78. ZHANG Yong-bao, HU Zhen-wen. Discussion on Enhancing the Technique of "Bridge on Bridge"[J]. Journal of Shijiazhuang Railway Institute, 1997, 10(2):75-78. |
| [4] | 侯宁, 韩万水. 特重车通过大跨石拱桥安全评定及加固措施研究[J]. 公路交通科技, 2011, 28(2):70-76. HOU Ning, HAN Wan-shui. Research on Safety Evaluation and Strengthening Method for Overweight Vehicle Pass through Stone Arch Bridge[J]. Journal of Highway and Transportation Research and Development, 2011, 28(2):70-76. |
| [5] | 方纳新, 王树栋, 娄国充. 一种保障超重车辆过桥的临时加固法[J]. 公路交通科技, 2002, 19(1):58-60. FANG Na-xin, WANG Shu-dong, LOU Guo-chong. A Temporary Bridge Reinforcement Method for Overweight Vehicles[J]. Journal of Highway and Transportation Research and Development, 2002, 19(1):58-60. |
| [6] | 邢文榜. 桥上桥在超重大件运输中的应用研究[J]. 中外公路, 2011, 31(4):174-177. XING Wen-bang. Application of Bridge on Bridge in Overweight Transport[J]. Journal of China & Foreign Highway, 2011, 31(4):174-177. |
| [7] | 郑一峰, 黄侨, 何红丽, 等. 漳州战备大桥极限承载能力分析[J]. 公路交通科技, 2010, 27(2):60-64, 70. ZHENG Yi-feng, HUANG Qiao, HE Hong-li, et al. Analysis on Ultimate Load Bearing Capacity of Zhangzhou Combat Readiness Bridge[J]. Journal of Highway and Transportation Research and Development, 2010, 27(2):60-64, 70. |
| [8] | 严波, 周余辉, 宋殿义. 装配式公路钢桥临时加固梁桥实例分析[J]. 公路, 2009, 54(2): 22-24. YAN Bo, ZHOU Yu-hui, SONG Dian-yi. Example Analysis of Temporary Reinforcement of Girder Bridge for Prefabricated Highway Steel Bridge[J]. Highway, 2009, 54(2):22-24. |
| [9] | 胡业平, 张志, 屠义强. 利用原桥提高桥上桥承载力问题[J]. 解放军理工大学学报:自然科学版, 2005, 6(3):270-274. HU Ye-ping, ZHANG Zhi, TU Yi-qiang. Enhancing the Carrying Capacity of Bridge on Bridge using Pristine Bridge[J]. Journal of PLA University of Science and Technology, 2005, 6(3):270-274. |
| [10] | 卢耀祖, 李悦. 有限元计算中用间隙元模拟非线性弹性支承[J]. 上海汽车, 1997, 4(4):5-6, 11. LU Yao-zu, LI Yue. Simulation of Nonlinear Elasticsupport Using Gap-Element in FEM[J]. Shanghai Auto, 1997, 4(4):5-6, 11. |
| [11] | 李盼到. 红枫湖特大桥施工控制[D]. 大连:大连理工大学, 2003. LI Pan-dao. Construction Control of Hongfenghu Grand Bridge[D]. Dalian:Dalian University of Technology, 2003. |
| [12] | 颜东煌, 田仲初, 李学文. 桥梁结构电算程序设计[M]. 长沙:湖南大学出版社, 1999. YAN Dong-huang, TIAN Zhong-chu, LI Xue-wen. Program Design of Bridge Construction[M]. Changsha:Hunan University Press, 1999. |
 2015, Vol. 31
2015, Vol. 31
