扩展功能
文章信息
- 罗滔, 陶庆东, 吴瑾
- LUO Tao, TAO Qing-dong, WU Jin
- 基于实测数据的沥青混凝土路面结构温度场特性分析
- Analysis of Temperature Field Characteristics of Asphalt Concrete Pavement Structure Based on Measured Data
- 公路交通科技, 2015, Vol. 31 (10): 30-36
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (10): 30-36
- 10.3969/j.issn.1002-0268.2015.10.006
-
文章历史
- 收稿日期: 2015-07-17
2. 重庆交通大学 土木建筑学院, 重庆 400074;
3. 苏州中材建设有限公司, 江苏 苏州 215300
2. School of Civil Engineering & Architecture, Chongiqing Jiaotong University, Chongqing 400074, China;
3. Suzhou Mid-material Construction Co., Ltd., Suzhou Jiangsu 215300, China
沥青混凝土路面材料的组成复杂,对外界因素的敏感性也很复杂,当外界环境因素发生变化时,路面结构各层内就会产生不稳定的热流,进而在路面结构各层材料之间就形成了温度场。路面各层结构材料的组成及约束条件不同,各层结构的感温性能及在温度场作用下的变形方式也不同,进而在沥青混凝土路面结构内产生了温度应力。由于路面结构材料在不同温度时的蠕变非线性效应不同,因此,综合考虑路面结构材料非线性条件下的温度场及温度应力变得十分复杂,在车辆荷载作用下路面产生裂缝及车辙等病害。
国内较多学者对沥青路面温度场进行了研究,陈嘉祺[1]对沥青路面温度场分布规律进行探讨,并拟合了温度场理论经验模型。杨学良[2]运用数值模拟方法对沥青路面温度场与结构耦合关系进行分析。谢来斌[3]运用ABAQUS软件与Ansys有限元软件对沥青混凝土路面温度场有限元模拟比较,验证了温度场分布规律的准确性。
由以上研究可以得出,温度随着外界环境的变化而改变,因此研究沥青混凝土路面结构的温度场影响因素及不同因素的影响程度非常有必要。基于实测数据,并运用ABAQUS有限元软件及其子程序建立沥青混凝土路面有限元模型,综合考虑沥青路面材料的蠕变非线性效应、温度、太阳辐射、风速的变化,研究沥青路面结构温度场随相关参数的变化与分布规律。
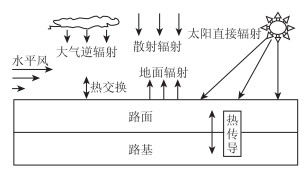
1 温度场传热学理论路面结构温度场形成的主要方式有:辐射、对流及传导。外界环境与路面结构热量相互作用[2],如图 1所示。
|
| 图 1 沥青路面与环境因素相互作用的温度场示意图 Fig. 1 Schematic diagram of temperature field of interaction of asphalt pavement with environmental factors |
路面结构的热流传递[4]随着外界环境的周期性变化而变化,假设路表通过对流和辐射从外部吸收的热量分别为p和r,根据能量守恒原理,得到不同时刻路面结构体内温度场T(x,y,z,t)应满足的平衡方程为[3]:
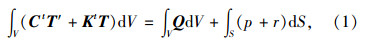
路表的热对流p可用Newton冷却方程表示,即:
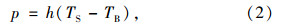
路面吸收及反射的太阳辐射能量得到的净热量r可表示为:
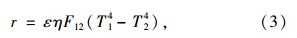
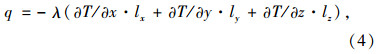
式(4)为路面结构体内的热传导方程,其符合Fourier定律。式中,q为热流密度;λ为导热系数;lx,ly,lz分别为边界表面向x,y,z外法线的方向余弦;∂T/∂x,∂T/∂y,∂T/∂z分别为x,y,z方向的温度梯度;“-”为热量由高温处向低温处流动。
由于沥青混合料具有对温度的敏感性,可得:
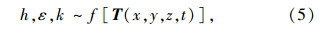
由式(1)~式(5)得到:
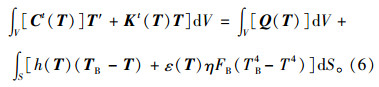
由式(6)可得,影响温度场结果的因素较多,其计算结果是非线性的。其中,风速、日最高、最低温度、云量、辐射量、路面反射率、日照时间及降水等因素均会影响路面与外界环境的传热方式。影响温度场最主要的因素是路面结构材料的热工性能参数及大气温度。
2 有限元模型建立为与简化的路面设计理论相对应,保证较好的计算效率,主要从平面应变问题的角度研究路面结构的温度场,建立沥青道路二维结构有限元模型,假设路面各结构层均匀连续、层间接触无热阻存在、路面材料热物性参数不随环境变化、各向同性、具体的路面结构参数[5]如表 1所示。
在分析温度场对路面结构热量交换的过程中,对路面材料热特性[6]的具体取值见表 2。
2.1 太阳总辐射及ABAQUS子程序本模型的ABAQUS子程序基于式(7)的近似模拟函数进行编写,由于ABAQUS有限元软件中并未包含上述表达式的计算方法,运用软件中提供的UMAT子程序进行二次开发,增强了软件的适用性、灵活性及解决实际道路工程问题的能力。太阳总辐射能量[7, 8]计算公式如下:
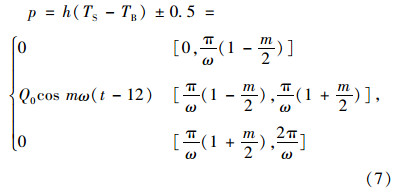
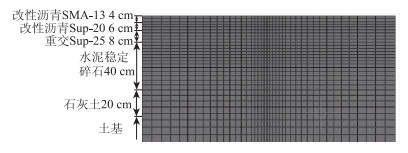
根据表 1及表 2中结构参数,应用ABAQUS软件及子程序建立有限元模型,单元采用八节点二次传热四边形单元DC2D8。有限元模型网格划分时,网格采用通常划分方法,网格划分针对性不强,为建立相对合理的道路温度场分析模型,对模型中部及其附近的网格进行加密,以便得到更为精确的温度场数值分析结果。沥青路面二维有限元模型[9],如图 2所示。
| 结构层 | 厚度/cm | 抗压弹性模量E/MPa | 泊松比μ | |
| 计算弯沉 | 计算拉应力 | |||
| 面层 | 18 | 1 200 | 2 000 | 0.25 |
| 基层 | 40 | 1 500 240~4 800 |
3 600 400~8 000 |
0.20 |
| 底基层 | 20 | 300 | 2 000 | 0.20 |
| 路基 | — | 45 | 30 | 0.35 |
| 结构参数 | 沥青面层 | 水泥稳定碎石 | 石灰土 | 土基 |
| 热传导率k /(J·m -1·h·℃) | 4 680 | 5 616 | 5 148 | 5 616 |
| 密度ρ /(kg·m -3) | 2 300 | 2 200 | 2 100 | 1 800 |
| 热容量C /(J·kg -1·℃) | 924.9 | 911.7 | 942.9 | 1 040 |
| 太阳辐射吸收率αs | 0.90 | |||
| 路面发射率ε | 0.81 | |||
| 绝对零度值TZ/℃ | -273 | |||
| Stefan-Boltzmann常数σ/(J·h-1·m2·K4) | 2.041 092×10-4 | |||
|
| 图 2 路面结构有限元模型 Fig. 2 The pavement structure finite element model |
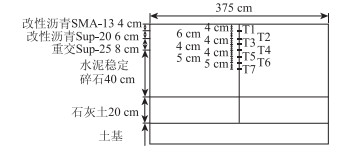
对重庆市南岸区某沥青混凝土试验路段长达一年观测,并考虑风速的不稳定及测定难度大的特点。采用年平均风速2.6 m/s,采用PT100铂电阻温度传感器,每间隔1 h利用温度记录仪采集一次数据。采用TBQ—2太阳总辐射表采集太阳辐射能量,每5 min 记录一次数据,传感器的埋设位置如图 3所示。在实测数据的采集过程中,对数据进行了相应的统计及筛选,同时,在道路结构面层表面向路面结构内共布置了7个传感器(T1~T7),以便测得不同深度的温度场。传感器的编号见表 3。
|
| 图 3 试验装置设置图 Fig. 3 Layout of test devices |
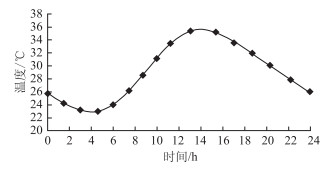
以重庆市2013年11月25日南岸区某沥青混凝土路面的24 h实测数据为基础,对测得数据进行了有效筛选及统计分析[10, 11],其日温度周期变化曲线,如图 4所示。
|
| 图 4 2013-11-25全天气温变化曲线 Fig. 4 Daily temperature curve of 2013-11-25 |
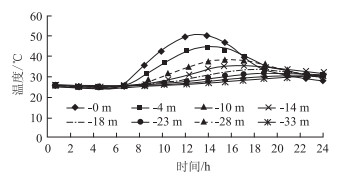
根据图 4的温度曲线,得到路面结构不同深度处温度曲线,如图 5所示。
|
| 图 5 路面结构不同深度处的日温度-时间曲线 Fig. 5 Daily curves of temperature vs. time of pavement structure in different depths |
由图 5可得,沥青路面结构内不同深度的温度场随外界温度的变化而变化,随着深度的增加,温度的变化速率越来越小,沥青面层表面的温度变化速率远远超过面层内部及底部,当达到一定路面结构深度以后,温度随时间的变化基本平稳,其中,半刚性基层的温度场随外界大气温度及时间的变化速率很小。
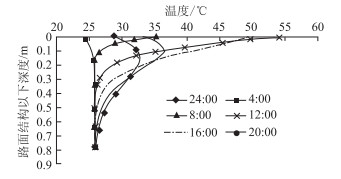
由图 6可得,随着外界环境温度的上升与下降,沥青路面结构中出现了正温度梯度和负温度梯度。对于正温度梯度,其路面结构表面的温度大于路面结构下部的温度;对于负温度梯度,其路面结构表面的温度小于路面结构下部的温度,随着外界环境的升温与降温,路面结构内的温度梯度从正到负再到正。温度梯度的变化在面层比较显著,对于水泥稳定碎石基层及石灰土基层,温度梯度基本没有发生变化。以上结果表明:大气温度变化对沥青路面上部的面层温度场影响很大,超出一定深度范围以后影响很小。
|
| 图 6 全天不同时刻的温度-结构深度曲线 Fig. 6 Daily curves of temperature vs. structure depth at different time |
在面层范围内(面层厚度为14 cm),不同时刻沥青路面面层内的温差相差很大,相差最大值发生在12:00,达到了25 ℃;相差最小值发生在20:00和24:00,其值均为1.3 ℃,原因主要是,每天12:00为外界温度最高的时刻,此时,面层表面的温度还未传递到面层底,致使面层表面与底面的温差相差很大。而随着夜晚的来临,面层内部的热量开始向外释放,当在20:00和24:00期间时,白天产生的热量已基本释放完毕,从而使得面层表面与底面的温度差很小。
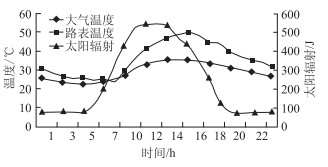
3.2 气象条件对路面结构温度场影响太阳辐射电流表是基于热电效应工作原理,且与太阳总辐射表配套使用的二次仪表,将电流表测得数据经过换算后,即为太阳辐射值。在选取大气温度参数时,以最高温度超过40 ℃的天气为高温天气;最高温度低于30 ℃的天气为低温天气;最高温度介于30~40 ℃的天气为中温天气。分别选取2012~2014年不同季节的代表数据,其数值曲线如图 7~图 9所示。
|
| 图 7 2012-05-04路表温度、大气温度与太阳辐射的日变化曲线 Fig. 7 Daily curves of road surface temperature, air temperature and solar radiation 2012-05-04 |
|
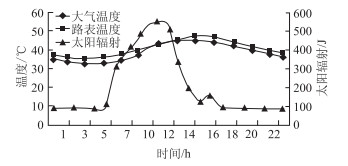
| 图 8 2013-08-09路表温度、大气温度与太阳辐射的日变化曲线 Fig. 8 Daily curves of road surface temperature, air temperature and solar radiation of 2013-08-09 |
|
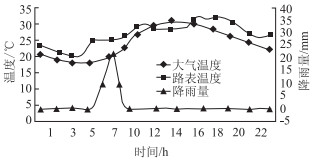
| 图 9 2014-02-28阴天路表温度、大气温度与太阳辐射的日变化曲线 Fig. 9 Daily curves of road surface temperature, air temperature and solar radiation of 2014-02-28 (cloudy) |
由图 7~图 9可得,随着太阳辐射的增强,大气温度与路表温度随之增加;路表温度与大气温度曲线变化趋势一致,路表温度普遍高于外界大气温度,路表温度峰值相比于大气温度峰值,呈现一定的滞后性[7]。
图 8、图 9为一年中高温日与低温日路表的温度、大气温度与太阳辐射之间的关系。由图中可以得出,路表温度、大气温度随着太能辐射能量的波动而波动,即表现出太阳辐射增加或降低、路表温度和大气温度升高或降低,但路表温度与大气温度随太阳辐射能量的变化具有一定滞后性,滞后时间大约为3.5 h。
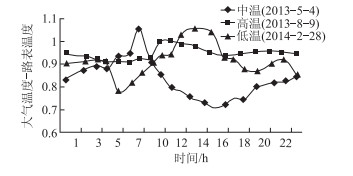
由图 10可知,在高温天气时,大气温度与路表温度的比值为0.9~1.01;中温(年平均温度)天气时,大气温度与路表温度的比值为0.71~1.05;低温天气时,大气温度与路表温度的比值为0.779~1.05。且可以得出,在每天6:00—18:00,大气温度对路表温度的贡献比例在中温天为0.717~0.942;高温天为0.923~0.997;低温天为0.8~1.05。在中温、高温天随着太阳辐射能量的增加,大气温度与路表温度的比值处在全天较低的阶段,大气温度对路表温度的贡献随着太阳辐射能量的增加贡献值下降,但仍高于70%。这表明在中高温天气时,大气温度对路表温度的影响随着太阳辐射的增加而减小,但贡献值仍然高于70%。由于每天太阳辐射的产生时间在6:00—18:00,其余时间受太阳辐射的影响很小,此时的太阳辐射能量几乎为零,此时路表温度场主要受到大气温度的影响。在中温天、高温天、低温天,大气温度对路面温度贡献比例约为0.71~1.05,表明无论是白天还是夜间,大气温度会影响全天的路表温度,是影响路面结构温度场及日温度峰值的主要因素。
|
| 图 10 不同气温-大气温度与路面温度的比值 Fig. 10 Curves of temperature vs. ratio of air temperature to surface temperature |
不同风速[12, 13, 14]下的路面对流系数可以通过式得出:
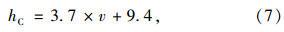
| 风速差/(m·s-1) | 路基表面 | 路表下4 cm | 路表下10 cm | 路表下14 cm | ||||
| T max/℃ | T min/℃ | T max/℃ | T min/℃ | T max/℃ | T min/℃ | T max/℃ | T min/℃ | |
| 2.0 | 56.95 | 24.32 | 49.66 | 24.74 | 41.94 | 25.16 | 38.26 | 25.37 |
| 2.6~2.0 | -1.38 | -0.016 | -1.07 | -0.006 | -0.74 | -0.002 9 | -0.58 | -0.002 4 |
| 3.6~2.0 | -3.34 | -0.040 | -2.59 | -0.016 | -1.79 | -0.006 9 | -1.39 | -0.005 7 |
| 4.6~2.0 | -4.95 | -0.062 | -3.85 | -0.024 | -2.65 | -0.010 1 | -2.07 | -0.008 2 |
| 5.6~2.0 | -6.30 | -0.081 | -4.90 | -0.031 | -3.37 | -0.012 7 | -2.63 | -0.010 2 |
| 风速差/(m·s-1) | 路表下18 cm | 路表下23 cm | 路表下28 cm | 路表下33 cm | ||||
| T max/℃ | T min/℃ | T max/℃ | T min/℃ | T max/℃ | T min/℃ | T max/℃ | T min/℃ | |
| 2.0 | 35.42 | 25.504 | 33.24 | 25.6 | 31.67 | 25.662 1 | 30.512 4 | 25.702 |
| 2.6~2.0 | -0.45 | -0.002 3 | -0.356 | -0.002 2 | -0.29 | -0.002 3 | -0.232 1 | -0.002 2 |
| 3.6~2.0 | -1.09 | -0.005 3 | -0.856 | -0.005 2 | -0.68 | -0.005 2 | -0.556 1 | -0.005 2 |
| 4.6~2.0 | -1.62 | -0.007 6 | -1.265 | -0.007 4 | -1.01 | -0.007 4 | -0.819 7 | -0.007 4 |
| 5.6~2.0 | -2.06 | -0.009 4 | -1.606 | -0.009 2 | -1.28 | -0.009 2 | -1.038 2 | -0.009 2 |
由表 4可得,随着风速的增加,路面不同深度处的温度随之下降,且随着路表到结构深度33 cm,温度差的峰值从每天的13:00移动到了24:00,主要原因是:随着路面结构深度的增加,不同深度位置处与大气对流作用频率下降,只有当上层结构与大气对流完成之后,才能由其以下的结构与大气对流,从而使下层结构温度差峰值向后延迟。
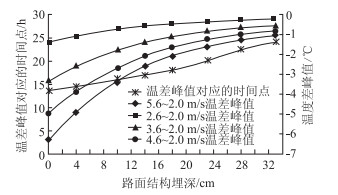
将表 4中的数据进行列表得到图 11,由图 11可以更为清晰地得到,随着风速的增加,路面结构的温度逐渐降低;随着风速差的增加,路面结构同一深度处的温度差也随着增加;不同风速差时,从路表到路面结构33 cm深度处,温度差的峰值及最小值逐渐增加;对于某一路面结构深度,随着风速差的增加,温度差逐渐增加。
|
| 图 11 不同风速时路面结构温差值变化曲线 Fig. 11 Curves of temperature difference of pavement structure at different wind speeds |
由图 12可得,从路表到路面结构33 cm深度处,温度差的峰值占到风速2 m/s时温度峰值的11.07%~3.4%,温度差的最小值占到风速2 m/s时温度对应值几乎为零。由以上结果表明,风速变化会对路面的温度场产生较大影响,应注意风速变化对温度场结果误差。

|
| 图 12 不同风速温差值占2 m/s风速温度值比例 Fig. 12 Ratio of temperature difference at different wind speeds to temperature at 2 m/s wind speed |
基于实测温度及太阳辐射能量数据,并运用ABAQUS有限元软件及其子程序建立沥青混凝土路面有限元模型,综合考虑沥青路面材料的蠕变非线性效应、温度、太阳辐射、风速的变化,得到温度场的分布规律,结论如下:
(1)随着沥青路面结构深度的增加,温度及其变化速率越来越小,当达到一定路面结构深度以后,结构内温度随时间的变化基本不变。
(2)无论是白天还是夜间,路表温度场受到大气温度对路面温度贡献比例约为0.71~1.05。大气温度是影响路面结构温度场的主要因素,是决定每天温度峰值的决定性因素,且路表温度与大气温度随太阳辐射能量的变化具有一定滞后性。
(3)风速变化会对路面的温度场产生较大影响,且随着风速的增加,路面结构不同深度处的温度随之下降,且路面结构温度差峰值向后延迟,主要由于当上层结构与大气对流完成之后,才能由其以下的结构与大气对流。
| [1] | 陈嘉祺,罗苏平,李亮,等.沥青路面温度场分布规律与理论经验预估模型[J].中南大学学报:自然科学版,2013, 44(4):1647-1656. CHEN Jia-qi,LUO Su-ping,LI liang,et al. Temperature Distribution and Method-experience Prediction Model of Asphalt Pavement[J]. Journal of Central South University:Science and Technology Edition, 2013,44(4):1647-1656. |
| [2] | 杨学良,刘伯莹.沥青路面温度场与结构耦合的有限元分析[J].公路交通科技, 2006,23(11):1-4,9. YANG Xue-liang,LIU Bo-ying. Coupled-field Finite Element Analysis of Thermal-stress in Asphalt Pavement[J]. Journal of Highway and Transportation Research and Development,2006,23(11):1-4,9. |
| [3] | 谢来斌,张倩,李彦伟.沥青混凝土路面温度场有限元模拟比较[J].公路,2013(7):38-42. XIE Lai-bin,ZHANG Qian,LI Yan-wei. Comparison of Two Asphalt Concrete Pavement Temperature Field Finite Element Simulations [J].Highway,2013(7):38-42. |
| [4] | 延西利,张世平,白伟,等.沥青路面温度场的热量分析研究[J].公路交通科技,2014,31(8):7-12. YAN Xi-li,ZHANG Shi-ping,BAI Wei, et al. Analysis on Heat of Temperature Field of Asphalt Pavement[J]. Journal of Highway and Transportation Research and Development,2014,31(8):7-12. |
| [5] | 李源渊,张亚鹏,孙建勇,等.沥青路面材料参数对路面温度场的影响研究[J].中外公路,2012,32(6):103-107. LI Yuan-yuan,ZHANG Ya-peng,SUN Jian-yong,et al. Study of Influence of Material Parameters of Asphalt Pavement on Pavement Temperature Field[J].Journal of China & Foreign Highway,2012,32(6):103-107. |
| [6] | 冯德成,胡伟超,于飞,等.沥青路面材料热物性参数对温度场的影响及敏感性分析[J].公路交通科技,2011,28(11):12-19. FENG De-cheng,HU Wei-chao,YU Fei, et al. Impact of Asphalt Pavement Thermophysical Property on Temperature Field and Sensitivity Analysis[J]. Journal of Highway and Transportation Research and Development, 2011,28(11):12-19. |
| [7] | 刘凯.沥青路面温度场分布规律研究[D].西安:长安大学,2010. LIU Kai. Study on Asphalt Pavement Temperature Field Distribution Pattern[D].Xi'an:Chang'an University,2010. |
| [8] | 秦健,孙立军.沥青路面温度场的分布规律[J].公路交通科技,2006,23(8):18-21. QIN Jian,SUN Li-jun. Study on Asphalt Pavement Temperature Field Distribution Pattern [J]. Journal of Highway and Transportation Research and Development,2006,23(8):18-21. |
| [9] | 廖公云,黄晓明.ABAQUS有限元软件在道路工程中的应用[M].南京:东南大学出版社,2008. LIAO Gong-yun,HUANG Xiao-ming. Application of ABAQUS Finite Element Software in Road Engineering [M].Nanjing: Southeast University Press,2008. |
| [10] | 曹久林.沥青路面温度场及应力场的数值模拟研究[D].重庆:重庆交通大学,2012. CAO Jiu-lin. Numerical Simulation of Temperature Field and Stress Field for Asphalt Pavement[D].Chongqing: Chongqing Jiaotong University,2012. |
| [11] | 单景松,杜贝贝.沥青路面温度场分析及全时域受力特性[J].公路工程,2014(1):73-77. SHAN Jing-song,DU Bei-bei. Analysis of Asphalt Pavement Temperature Field and Characteristics of Stress in all Time Domain [J].Highway Engineering,2014(1):73-77. |
| [12] | 韦璐,KAYSER S,WELLNER F.路表温度对沥青路面疲劳损伤的影响分析[J].公路交通科技,2013,30(1):1-5,16. WEI Lu, KAYSER S, WELLNER F. Impact of Surface Temperature on Fatigue Damage in Asphalt Pavement [J].Journal of Highway and Transportation Research And Development, 2013,30(1):1-5,16. |
| [13] | 韦金城,王林,杨永顺,等.永久性沥青路面试验路力学响应分布的数值仿真[J].公路交通科技,2010,27(6):15-19,33. WEI Jin-cheng,WANG Lin, YANG Yong-shun,et al. Numerical Simulation of Mechanical Response of Perpetual Road Test Asphalt Pavement[J].Journal of Highway and Transportation Research and Development, 2010,27(6):15-19,33. |
| [14] | 白琦峰,钱振东,李浩天,等.基于统计回归法的沥青路面温度场模型[J].公路交通科技,2011,28(11):27-31. BAI Qi-feng,QIAN Zhen-dong,LI Hao-tian,et al. Asphalt Pavement Temperature Field Model Based on Statistic Regression Method [J]. Journal of Highway and Transportation Research and Development,2011,28(11):27-31. |
 2015, Vol. 31
2015, Vol. 31
