扩展功能
文章信息
- 曹交交, 韩印, 姚佼
- CAO Jiao-jiao, HAN Yin, YAO Jiao
- 城市交通干线动态双向绿波优化控制模型
- A Dynamic Dual-direction Green Wave Optimization Control Model for Urban Arterial Roads
- 公路交通科技, 2015, Vol. 32 (9): 115-120
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 32 (9): 115-120
- 10.3969/j.issn.1002-0268.2015.09.019
-
文章历史
- 收稿日期: 2014-06-16
城市交通干线承受着整个城市的主要交通负荷,对干道实行绿波协调控制可以实现交通流合理的优化调度,从而提高整条干线的道路实际通行能力和服务水平。交通干线交叉口信号容易实现单向绿波带控制,但双向绿波带控制却一直没有很好的效果,是当前交通控制研究的难点和热点。
1 问题描述干道双向绿波协调控制信号配时优化方法是由J. T. Morgan与J. D. C. Little[1]于1981年提出的,他们建立了最大绿波带宽的混合整数线性规划模型——MAXBAND 模型,并采用Little建立的混合整数规划模型通过对公共周期、绿信比、最佳速度、相位差及相序方案等因子进行优化以获得最大带宽。Gartner等[2]在MAXBAND方法的基础上提出了复合绿波带宽的MULTIBAND模型,根据路段上的流量计算出与交通流量相适应的带宽,设计的MULTIBAND方法可得到最大带宽的干道协调效果,增大相邻交叉口间的协调率。在国内,王俊刚等[3]建立了以绿波带宽度为目标函数和以时差为决策变量的变带速干线协调控制数学模型,大大提高了绿波控制的效率。邵娟等[4]为了提高主干线的通行能力和服务水平,缓解交通拥堵状况,重点对各个交叉口信号进行合理配时并进行信号协调联动控制,以减少停车次数和延误,提高交通安全性并节约油耗减少空气污染。他们提出了交通干线绿波控制技术,利用Webster算法优化公共周期时长,由历史交通信息确定绿信比,根据现状车辆速度及路段间距离确定相位差,从而找到了合理的绿波带宽,以优化主干线的信号控制。
值得注意的是:首先,这些算法大都以求取最大绿波带宽为主要优化目标,仅仅考虑主要协调方向的车流而忽略了左转交通流的影响;其次,对排队延误时间和排队长度的动态变化对绿波控制的影响亦考虑不足,造成实际应用中的效果不甚理想;最后,由于双向绿波控制的实现需要相对苛刻的条件,许多研究者都集中于实现单向绿波,降低了城市干道的服务水平。
基于此,本研究通过对左转相位和排队长度的优化,结合动态双向绿波控制的特点,提出了一种新的城市交通干线动态双向绿波优化协调控制方案,并通过案例分析对其有效性与实用性进行验证。
2 基本假设城市交通干线动态绿波控制主要应用于低饱和度和交叉口间距适中的情况,为了便于描述,本研究基于以下假设:
(1)非机动车跟随交通信号控制通行,人为或其他非机动车辆的干扰较小。
(2)干线每个交通控制信号周期中的相序和相位数量确定不变,且在每个相位之间不设置时间间隔。
(3)路口各车流分为左转、直行和右转3股车流,右转车辆不受信号相位的单独控制,在确定的某一时段里,转弯车流的比率相对固定且转向选择服从泊松分布[5]。
(4)左转车道在交叉口内部没有排队空间,且在左转车流不顺畅的情况下需设置左转车道。如果不能设置专用左转车道,则应全天或部分时间禁止左转车流通行,同时要给左转车辆提供可选择的出路。
(5)相邻两路口有一定距离,一般情况下都假定在400~1 000 m之间存在较高的控制关联度[6],当两个交叉口相距较近且车流量较大时,可将其视为一个交叉口;当两个交叉口相距较远时,可视为单独的交叉口进行控制。
3 模型构建 3.1 双向绿波的控制方式假定某城市交通干线有N个交叉口,本文考虑由西向东的两个相邻交叉口n和n+1,东西向道路为主干道,南北向道路为支路,选择典型的十字路口,每个方向有直行、左转、右转车道,每个车道都埋设有两个感应线圈,同一车道前、后两个环形线圈相距80~300 m,可检测车流量及排队长度。
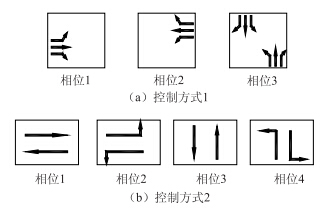
在双向绿波控制中,最常用的两种控制方式如图 1所示。
|
| 图 1 双向绿波的常见控制方式 Fig. 1 Common control modes of dual-direction green wave |
控制方式1适用于左转车流量比较大的情形。当系统运行时,由于相邻交叉路口间的路段长度和车流平均速度的不同,会出现3种情况:相位1和相位2连续;相位1和相位2重合;相位1和相位2离散。所以该控制策略中相位数和相序是不固定的,同时必须根据干线上各路口的相位差和实际交通流状况来确定。当相位1和相位2的左转车辆与直行车辆发生冲突,必要时可通过对左转相位的早断和迟起来避免。
控制方式2是最常用的四相位控制策略,应用范围较广,适用于车道多、行人较多的情形。信号相位设计不但要考虑相位组合还要考虑相位衔接,控制方式1中相位数和相序是不固定的,在时间上不一定保证相互之间的连续性,具体实施中有一定的困难,且适用于左转车流量较大的情形,不具有普遍应用意义,而控制方式2的相位数和相序固定且对称设计,方便驾驶员理解,同时应用范围广,具有普遍性。
本研究的每个路口的红绿灯以常用的四相位控制策略为例,根据实际交通经验,每一相位时间不能过短,以免某相位绿灯时间过小,使车辆不能及时通过路口而影响交通安全,一般最短相位时间不小于15 s,信号周期也不能过长,一般不超过220 s,否则会由于某相位的绿灯时间太长而使驾驶员心理上难以承受。
3.2 绿时差动态优化模型在双向道路的绿波设计时,时距图中相向方向的绿波到达某交叉口时分别有一个时刻点,根据两者之间的位置关系可以将上行绿波和下行绿波到达交叉口的时刻点分为重合、靠近和远离3种。
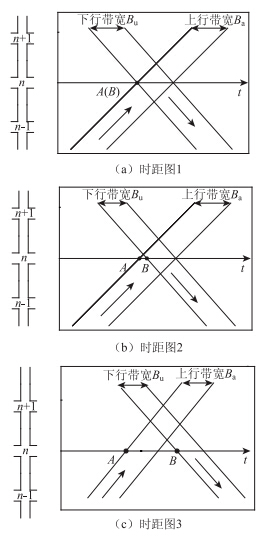
理想的相向方向的绿波带时刻点重合即上行绿波和下行绿波到达某交叉口的时刻相等,此时上行绿波带宽和下行绿波带宽相等且达到最大,为该相位的有效绿灯时间。如图 2(a)所示,以交叉口n为例,从交叉口n到n+1定义为上行,设上行绿波和下行绿波与交叉口n的交点分别为A和B,理想情况下A点和B点重合,但在实际交通流中,由于相位差的取值受交叉口的排队长度、损失时间、红灯时长、路段平均行驶时间等的约束,致使该时刻点相互靠近和远离,如图 2(b)和2(c)所示,(b)图中A点和B点靠近,相较于理想时刻有一定偏差,而(c)图中A、B点相互远离,导致了有效绿灯时间的浪费,降低了干道车辆的通行效率。
|
| 图 2 交叉口双向交通干线绿波时距图 Fig. 2 Time-space diagrams of intersection dual-direction green wave |
依据双向绿波信号控制的特点,本文针对图 2(b) 和2(c)出现的情况,通过对绿时差的动态优化,使配时得到的上、下行绿波到达交叉口的时刻差值最小,生成交通信号相位的动态配时方案,从而使上、下行绿波带宽都达到最大值,实现城市交通干线动态双向绿波控制。本模型先拟定控制范围,按有关理论确定各交叉口的公用周期和绿信比,再按交叉口间相位差和有关规定确定上、下行绿波带时间差模型,在系统周期和绿信比不变的条件下,通过以下模型对时差优化,获得总带宽最大的优化方案[7]。
假定协调相位为东西直行相位,考虑东西向和西东向两个方向实现绿波控制,设Δtn+1,n(k)为第k个周期交叉口n和n+1的绿波控制相对相位差,相位差的取值受到交叉口的排队长度、损失时间、红灯时长、路段平均行驶时间约束[8],则:
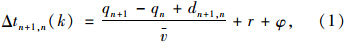
式中,Δtn+1,n(k)为第k个周期交叉口n+1和n的绿波控制相对相位差;qn+1为交叉口n+1停车线前的排队长度;qn为交叉口n停车线前的排队长度;dn+1,n为交叉口n+1和交叉口n之间的距离; 为路段的平均速度;r为红灯时间;φ为补偿系数,是对于司机反应时间、相位转换时间及黄灯时间的补偿。
为路段的平均速度;r为红灯时间;φ为补偿系数,是对于司机反应时间、相位转换时间及黄灯时间的补偿。
设第k个周期,上行绿波带到达交叉口n对应的A点时刻为Tna(k),下行绿波带到达交叉口n对应的B点时刻为Tnu(k),a表示上行,u表示下行,tna(k) 和tn+1u(k)分别为第k个周期上行绿波带到达交叉口n和下行绿波带到达交叉口n+1的理论开始时间,则
上行绿波A点时刻
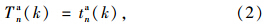
下行绿波B点时刻
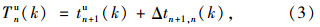
则可推算出上、下行绿波到达交叉口n的时刻差ΔTn(k)为:
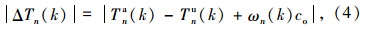
式中,ωn(k)为能使ΔTn(k)最小的整数;co为信号周期,即:
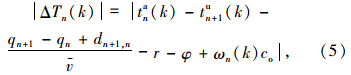
则可通过如下模型来对干道进行双向绿波实时控制:
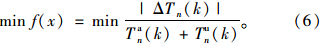
具体的控制目标表达如下:
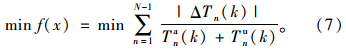
为了保障绿波带的连续性和稳定性,这里增加如下约束条件[9]:
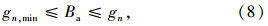

式中,Ba为绿波带上行带宽;Bu为下行带宽;gn为交叉口n控制方向直行相位绿灯时长;gn,min为交叉口n控制方向直行相位最小绿灯时长。
该模型的建立使上、下行绿波带在交叉口n的时间差值达到最小,从而确保了上、下行带宽的最大化,提高了干道车辆的通行效率。
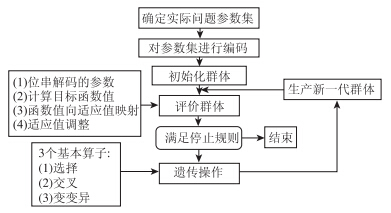
3.3 模型求解采用遗传算法求解。首先,直接以目标函数作为搜索信息不需通过复杂的推导和变换来获得可求解的模型;其次,遗传算法使用概率搜索技术,在搜索计算过程中不易陷入局部最优;最后,不受搜索空间诸如连续性、可导和单峰等条件的约束,而在协调控制各种参数中,相位差自身为多维参数,其维数随着协调交叉口数量的增加而增加[10],根据遗传算法的特点并结合上述相位差参数特征,采用遗传算法对模型求解,其流程如图 3所示。
|
| 图 3 遗传算法流程图 Fig. 3 Flowchart of genetic algorithm |
在遗传算法优化过程中,以上、下行绿波到达交叉口的时刻差值最小为目标函数,即以f(x)=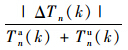 为适应度函数,约束条件为Δtn+1,n(k)>0,具体步骤如下:
为适应度函数,约束条件为Δtn+1,n(k)>0,具体步骤如下:
(1)根据每个交叉口的平面布局及计算交通量,按单点实时控制的配时方法,确定每个交叉口所需的周期时长并以所需周期最大的交叉口为关键交叉口,最大周期时长即为线控系统的备选系统周期时长。根据周期时长的约束范围来确定交叉口各相位的有效绿灯时间范围[11]。
(2)以各信号交叉口的相位差为基因,对其采用二进制编码,构造染色体从而形成种群。
(3)控制参数主要包括种群规模、执行不同遗传操作的概率及其他辅助性参数。本研究初始化交叉概率pc=80%,变异概率pm=10%,为防止出现局部搜索能力差的问题,提高遗传算法的收敛性能,在用遗传算法优化时,比较本次及相关的前两次的最优个体适应度,如果它们都相等,则在保留当前最优个体的前提下,将交叉概率减去系数λ=0.01,变异概率加上系数θ=0.01,即pc=pc-λ,pm=pm+θ。通过这种适当增大变异概率而减少交叉概率的方法,可提高遗传算法的局部收敛能力,避免出现未成熟收敛现象。
(4)确定算法的终止准则。规定最大演化代数为100,当演化代数达到100时,算法终止。
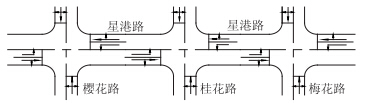
4 案例分析现以江苏省常州市东西走向干道星港路的调查数据为依据,对城市交通干线动态双向绿波控制模型进行实例分析。星港路全线以东西向交通流量为主,南北向交通流量为辅,其中东西向为双向四车道,南北向为双向两车道,高峰、平峰车流量变化不大,实际平均车速60 km/h。选取东西流量较大的樱花路、桂花路和梅花路3个路口,如图 4所示。已知这3个交叉口路口的间距,各路口的车道功能和现状交通流量需求等信息如表 1所示。
|
| 图 4 星港路与樱花路、桂花路、梅花路交叉口 Fig. 4 Intersections of Xinggang Road with Yinghua Road,Guihua Road and Meihua Road |
| 交叉口 | 东进口流向 | 西进口流向 | 南进口流向 | 北进口流向 | |||||||||
| 左 | 直 | 右 | 左 | 直 | 右 | 左 | 直 | 右 | 左 | 直 | 右 | ||
| 星港路-樱花路路口 | 车道数 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||
| 流量/(veh·h-1) | 107 | 686 | 55 | 301 | 755 | 99 | 33 | 148 | 119 | 37 | 161 | 101 | |
| 星港路-桂花路路口 | 车道数 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||
| 流量/(veh·h-1) | 106 | 709 | 45 | 244 | 595 | 72 | 41 | 132 | 108 | 37 | 167 | 98 | |
| 星港路-梅花路路口 | 车道数 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||
| 流量/(veh·h-1) | 93 | 715 | 64 | 114 | 572 | 54 | 52 | 123 | 110 | 42 | 160 | 95 | |
| 注:星港路-樱花路路口距下一路口间距460 m;星港口-桂花路路口距下一路口间距456 m | |||||||||||||
本案例中交叉路口各方向车辆的到达数服从泊松分布,车辆在交叉口的转向是随机的,左转、直行和右行的概率分别为12%,80%,8%,遗传算法的种群大小设置为80,终止代数为100,仿真时扫描步长设为1 s,主干道星港路及相邻交叉口采用本研究方法与传统MAXBAND方法比较的结果如表 2所示。可以看出,动态双向绿波带控制策略使主干线平均延误时间改善16.85%,平均停车率改善9.54%,平均排队长度改善14.28%,相邻的交叉口在相应方面均有一定程度的改善,效果十分明显,是进行城市交通控制有效且实用的方法。
| 交叉口 | 方法 | 平均 延误/s | 平均停车 率/% | 平均排队 长度/m |
| 星港路- 樱花路路口 | MAXBAND模型 | 38 | 84 | 29.6 |
| 本研究方法 | 34 | 79 | 22.7 | |
| 改进率/% | 10.53 | 5.95 | 23.31 | |
| 星港路- 桂花路路口 | MAXBAND模型 | 32 | 84 | 25.4 |
| 本研究方法 | 24 | 74 | 20.9 | |
| 改进率/% | 25.00 | 11.9 | 17.72 | |
| 星港路- 梅花路路口 | MAXBAND模型 | 28 | 80 | 22.1 |
| 本研究方法 | 25 | 72 | 19.4 | |
| 改进率/% | 10.71 | 10.00 | 12.22 | |
| 星港路干线 | MAXBAND模型 | 100.3 | 48.2 | 12.6 |
| 本研究方法 | 83.4 | 43.6 | 10.8 | |
| 改进率/% | 16.85 | 9.54 | 14.28 |
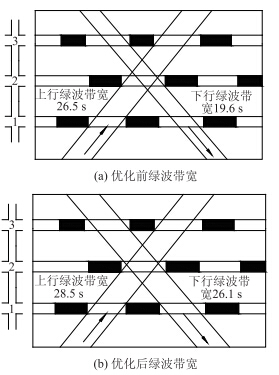
图 5显示了绿波带宽优化前后的情况,其中,图 5(a)为MAXBAND模型控制方式下的干线绿波时距图,以星港路-桂花路交叉口为基准交叉口,此时上行绿波到达交叉口的时刻为57.6 s,下行绿波为41.4 s,总带宽为46.1 s。图 5(b)为采用本研究控制方法优化后的时距图,上行绿波到达交叉口的时刻为59 s,下行绿波为56.5 s。各个交叉口的配时结果如表 3所示,可以看出,当干线双向绿波到达交叉口的时刻差值减少时,可以有效提高系统的绿波带宽,此时总带宽增加到54.6 s,大大提高了干线的通行能力。
|
| 图 5 星港路优化前后绿波带宽 Fig. 5 Time-space diagrams before and after optimization on Xingang road |
| 交叉口 | 东西直右 | 东西左转 | 南北混行 | |
星港路-樱花路 | 绿时分配/s | 52 | 18 | 20 |
| 绿信比 | 0.449 | 0.158 | 0.172 | |
星港路-桂花路 | 绿时分配/s | 52 | 16 | 22 |
| 绿信比 | 0.397 | 0.128 | 0.174 | |
星港路-梅花路 | 绿时分配/s | 58 | 8 | 24 |
| 绿信比 | 0.41 | 0.06 | 0.173 |
本文在分析城市干线系统控制方式的基础上,建立了以干线双向绿波到达交叉口的时刻差值最小为目标的交通干线信号动态优化控制模型,并采用遗传算法进行了求解,实现了城市交通干线动态双向绿波控制,避免了交通拥挤和堵塞。从仿真试验中可以得出,该算法优于静态绿波带控制方法,具有广阔的应用前景。
城市交通干线动态双向绿波控制能够适应实时动态交通演变,具有较强的实用性,而本文的研究假定有较大的通行能力,避免由于大量交通流引起相当部分的车辆滞留,把车辆的驶入驶出视为连续运行状态,能够与其他车辆衔接。研究的交通运行条件相对于实际复杂情况较为理想,同时文中是以3个交叉口为例。随着干线交叉口数量的增加,双向协调模型的效益与交叉口数量间的关系也有待进一步研究。
| [1] | LITTLE J D C, KELSON M D, GARTNER N H.Maxband:A Program for Setting Signals on Arteries and Triangular Networks[J].Transportation Research Record,1981,795:40-46. |
| [2] | GARTNER N H, ASSMANN S F, LASAGA F, et al. Multiband: A Variable-bandwidth Arterial Progression Scheme [J]. Transportation Research Record,1990, 1287:212-222. |
| [3] | 王俊刚,于泉,高颖,等.变带速干线协调控制模型研究[J].公路交通科技,2005,22(4):108-111. WANG Jun-gang, YU Quan, GAO Ying, et al. Variable Band Speed Arterial Coordination Control Model Research[J]. Journal of Highway and Transportation Research and Development,2005,22(4):108-111. |
| [4] | 邵娟,程琳.基于Synchro系统的干线绿波控制优化技术[J].公路交通科技,2013,30(9):116-121. SHAO Juan,CHENG Lin. Green-wave Control Optimization Technique of Arterial Roads Based on Synchro[J]. Journal of Highway and Transportation Research and Development, 2013,30(9):116-121. |
| [5] | 臧利林,贾磊,罗永刚.交通干线相邻交叉口动态协调控制研究[J].公路交通科技,2007,24(7):103-106. ZANG Li-lin, JIA Lei, LUO Yong-gang. Study on Dynamic and Cooperative Control for Neighboring Intersections on Traffic Arterial Roads[J]. Journal of Highway and Transportation Research and Development, 2007, 24(7):103-106. |
| [6] | 德国道路与交通工程研究学会.交通信号控制指南: 德国现行规范[M].李克平,译.北京:中国建筑工业出版社,2006: 47-51. Road and Traffic Engineering Research Society of Germany. Traffic Signal Control Guide: Germany Current Specifications [M].LI Ke-ping,translated.Beijing: China Architecture & Building Press,2006: 47-51. |
| [7] | 王俊刚,于泉,高颖.变带速干线协调控制模型研究[J].公路交通科技,2005,22(4):108-111. WANG Jun-gang, YU Quan, GAO Ying. Variable Band Speed Arterial Coordination Control Model Research[J].Journal of Highway and Transportation Research and Development, 2005,22(4):108-111. |
| [8] | 曹鹏.城市道路交通信号实时控制的数学模型[D].北京:北京交通大学,2010. CAO Peng. The Model of Real-time Traffic Signal Control of Urban Road[D].Beijing: Beijing Jiaotong University,2010. |
| [9] | 唐克双,孔涛,王奋,等.一种改进的多带宽干线协调控制模型[J].同济大学学报:自然科学版,2013,41(7):1002-1008. TANG Ke-shuang, KONG Tao, WANG Fen, et al. A Modified MULTIBAND Model for Urban Arterial Coordinate Control[J]. Journal of Tongji University: Natural Science Edition,2013,41(7):1002-1008. |
| [10] | 吴恩,杨晓光,吴震,等.基于遗传算法的干线协调控制参数共同优化[J]. 同济大学学报:自然科学版,2008,36(7):921-926. WU En, YANG Xiao-guang, WU Zhen, et al. Parameters Co-optimization for Artery Coordinated Control Based on Genetic Algorithm[J]. Journal of Tongji University: Natural Science Edition, 2008,36(7):921-926. |
| [11] | 仇东华.干线协调控制的研究与设计[D].合肥:中国科学技术大学,2009. QIU Dong-hua. Research and Design of Arterial Coordination Control[D]. Hefei: University of Science and Technology of China, 2009. |
 2015, Vol. 32
2015, Vol. 32
