扩展功能
文章信息
- 张孜, 宋奇文, 林思
- ZHANG Zi, SONG Qi-wen, LIN Si
- 动态可变车道在路网通行能力优化中的应用
- Application of Dynamic Reversible Lane in Road Network Capacity Optimization
- 公路交通科技, 2015, Vol. 32 (9): 109-114
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 32 (9): 109-114
- 10.3969/j.issn.1002-0268.2015.09.018
-
文章历史
- 收稿日期: 2014-05-20
2. 广州交通信息化建设投资营运有限公司, 广东 广州 510620;
3. 佛山市交通运行监测中心, 广东 佛山 528000
2. Guangzhou Communications Information Construction Investment and Operation Co., Ltd., Guangzhou Guangdong 510620, China;
3. Foshan Traffic Operation Monitoring Center, Foshan Guangdong 528000, China
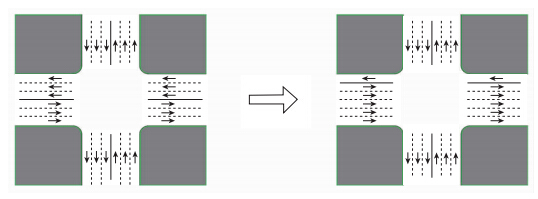
交通拥堵是当今城市交通系统面临的主要问题之一。可变车道通过临时改变某条车道的交通流方向,最大程度地利用未饱和车道的道路资源,以提高拥挤路段的交通通行能力。如图 1左侧所示,上方车道的利用率远大于下方车道。变换1条车道方向后,瞬时通行能力增加了50%(如图 1右方所示)。
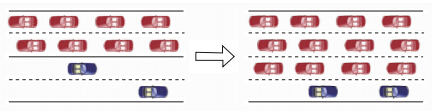
|
| 图 1 可变车道示意图 Fig. 1 Schematic diagram of reversible lane |
目前可变车道已在国内外多个城市使用,主要用于上下班高峰期有潮汐现象的道路或者发生交通事件需紧急快速撤离的地区[1, 2]。可变车道设置都经过前期详细调研和交通组织论证,很少有能力实施动态车道变换。随着智能交通技术的发展,道路流量监控系统已完成实时道路交通数据采集,交通控制系统有可能实现快速动态地打开或关闭某条车道,从而实现实时改变车道方向,有效提升交通系统通行能力。但是,车道方向的快速变化会对司机驾驶产生不利影响。为了充分利用动态可变车道的潜力,需要依靠辅助驾驶系统或自动驾驶车辆帮助车辆适应车道方向的快速变化。随着辅助驾驶系统的推出,交通管理者可应用可变车道策略提高城市道路的通行能力。
对于单个路段的调整是很容易实现的,但是对于一个城市的交通网络来说,某时段内可能存在十几段或几十段双向流量不平衡路段,而其中任一路段上车道方向的调整都会引起整个路网交通流量的变化,这些路段的调整是相互影响的。因此,不能孤立着眼于一条路段的调整,而忽略其他路段的调整,必须从系统角度,根据实际交通需求的变化来确定这些路段的车道调整方案,以达到交通网络系统性能指标最优[3, 4]。定义实施可变车道的目标如下:对于给定的道路网络、车辆位置和目的地,每个车道分配一定的交通流,使得网络效率最大化。为研究动态可变车道的网络效率,将该问题视为最大的多物网络流问题,并提出整数规划和双层规划模型计算网络中的最大流量。
1 动态可变车道技术框架可变车道是指车辆可在任意一个方向行驶的车道。常见的可变车道的硬件有高架交通灯,许多城市采用拉链机移动可移动的障碍,从而实现某方向的道路可占用另一方向的车道,动态地扩大车道数[3]。
动态可变车道的基本要求是车道反转须快速安全地完成,并且需提醒驾驶员立即改变车道。尽管这些要求在系统硬件设计时能满足,但是动态车道反转将显著增加驾驶员驾驶的风险。因此,车联网技术的应用对于动态可变车道的实施有重要作用。控制中心发出车道反转指令后,信息也实时通过无线网络传输到车载端,使汽车根据车道的变化迅速做出相应的反应。
2 可变车道通行能力分析 2.1 路段可变车道本文从理论的角度考虑可变车道对道路的影响。设R为交叉口I1和交叉口I2之间的道路,L1,2是从I1到I2的车道集合,L2,1为从I2到I1的车道集合,l1,l2,l3,l4为道路车道。图 2表明了其中一种场景L1,2={l1,l2}和L2,1=l3,l4。l1的通行能力c(L)指车道单位时间内可能通过的最大交通实体数。设车道集为L,其通行能力c(L)为所有车道的通行能力总和c(L)=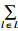 c(l)。为简单起见,忽略车辆变道和相邻车道间的影响。
c(l)。为简单起见,忽略车辆变道和相邻车道间的影响。
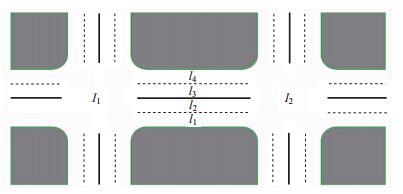
|
| 图 2 可变车道 Fig. 2 Reversible lane |
假设I1和I2产生交通量,道路R的最大交通通行能力为β(I1)和β(I2),实际交通流为λ(L1,2)和λ(L2,1),λ为常数。实际交通流受到道路通行能力的限制。因而有λ(L1,2)=min {β(I1),c(L1,2)}和λ(L2,1)=min{β(I2),c(L2,1)}。 如果λ(L1,2)=c[λ(L1,2)],则表明L1,2是饱和的。若β(I1)>c(L1,2),则L1,2过度饱和,超出道路通行能力 β(I1)-c(L1,2)。若β(I1)<c(L1,2),则L1,2未饱和,剩余交通通行能力为c(L1,2)-β(I1)。L2,1饱和度的定义方式相同。
道路R的通行量指各个车道有效交通量的总和,为λ(L1,2)+λ(L2,1)。现在考虑如果l∈L1,2车道方向反转后的影响。根据定义,道路的通行能力在车道变化后增加,当且仅当
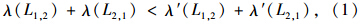
式中λ′(L1,2)=min{β(I1),c(L1,2)-c(l)},λ′(L2,1)=minβ(I2),c(L2,1)+c(l),通常情况下,当道路某方向过饱和而另一方向未饱和时(图 1),车道反转对于交通系统是有积极影响的,有如下定理。
定理1:定义道路R,La,b为道路R从a至b方向的车道集合,Lb,a为道路R从b至a方向的车道集合,l为La,b中任一车道。如道路R的通行能力在车道l∈La,b反转后增大,则La,b是未饱和的,其剩余交通通行能力为δa;如Lb,a是过饱和状态,超出通行能力为δb,需满足max{c(l)-δa,0.0}<δb。
证明:限于篇幅,只考虑c(l)>δa且δb<c(l)的情况。车道l反转减少了Lb,a的通行能力,减少量为x=c(l)-δa>0。同时,La,b有效交通流增加了δb。当满足δb>x=max{c(l)-δa,0.0}时,整个道路的交通通行能力增加。
2.2 交叉口可变车道由于交叉口经常是交通流的瓶颈,阻止临近道路达到定理1所预测的最大交通通行能力。因此,有必要分析实施可变车道对交叉口通行能力的影响。
采用实证法验证交叉口应对临近车道反转导致交通流变化的能力。交叉口模拟试验见图 3,该交叉口每个方向道路有6条车道,其中3条车道为进口车道,3条车道为出口车道。设定东行方向目标交通流为5 500 pcu/h,西行方向目标交通流为1 100 pcu/h,南行和北行目标交通流均为1 650 pcu/h。在该情形下,东行方向交通需求远高于其他方向,造成东行方向交通拥堵。检验西行方向车道变化是否有助于提高东行方向道路的通行能力以及路口通行能力。车道反转后,新的车道配置如图 3右侧所示。
|
| 图 3 交叉口可变车道模拟图 Fig. 3 Simulated reversible lane at intersection |
总共进行了30次反复试验。每次运行测量以下指标:1 h内进入交叉口的车辆总数,1 h内每个方向进入交叉口的车辆总数。测试结果见表 1。结果表明,在95%的置信区间内,车道反转后,交叉口的通行量增加了6% ,这主要是因为东行方向进入交通流提高了13%。同时,由于其他方向车道是不饱和的,车道反转对其通行能力影响较小。
| 行车位置 | 实施前/ (pcu·h-1) | 实施后/ (pcu·h-1) | 变化/% |
| 东行方向 | 4 608.5±8.4 | 5 218.0±11.3 | 13.30 |
| 西行方向 | 1 180.5±14.1 | 1 126.7±9.6 | -5.40 |
| 北行方向 | 1 711.6±11.3 | 1 702.6±13.1 | -0.70 |
| 南行方向 | 1 710.8±13.6 | 1 714.5±12.5 | -0.10 |
| 交叉口 | 9 172.3±31.7 | 9 875.8±25.2 | 6.40 |
可变车道在提高单条道路和交叉口通行能力的作用已得到证实,目前面临的问题是动态可变车道的设置能否提高路网整体的通行能力。采用图论来模拟路网,图论中包含节点和边,每个节点代表交叉口,边代表交叉口间的道路。其中,网络的边用u,v表示,每条边相应的通行能力记为c(u,v),反映该条道路所能承受的最大交通量。网络中的交通需求是有限的,与交通需求相关的要素包括交通产生点、目的地点和需求量。在图论模型试验中需确定:(1)给定的路网能否动态配置车道以适应动态交通流的变化;(2)路网能承担的最大交通负荷。
多物网络流问题是多种物品在网络中从不同的源点流向不同的汇点的网络流问题。采用图论模拟道路交通网络,动态车道配置问题转换为多物资网络流问题,并采用线性规划解多物网络流问题[5]。
2.3.1 整数线性规划线性规划用于求解一组受约束变量的最大化线性函数。在普通线性规划中,变量可以是分数,本研究中所有的交通流是整数值,需采用整数线性规划模型。定义以下整数线性规划:给定一个图G=V,E,其中,V为节点集合,E为边集合。每条边(u,v)具有一定的整数交通通行能力c(u,v),假设每条道路具有k个不同方向交通流,记为K1,…,Kk,其中每个交通流Ki=(si,ti,di)有相关联的出发点si、目的地ti和交通需求di,边(u,v)的交通流表示为fi(u,v)。
研究目标是要找到满足以下约束条件的交通流分配:通行能力约束如式(2)所示,一条边(u,v)两个方向的交通流不得超过该边的容量。守恒约束如式(3)所示,确保所有汇聚/源节点的交通流流入等于交通流流出。式(4)规定了各交通流必须达到或超过该交通需求[6, 7]。
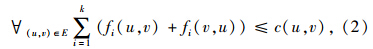
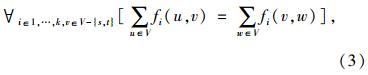
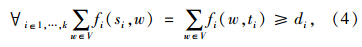
式中,i为网络边上某一交通流方向;w为网络节点。
用ILP求解器求解目标函数最大化的交通流分配方式。选择最大化多商品目标函数,目标是重新配置网络最大限度地提高流量:
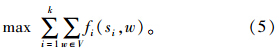
多物网络流问题求解的最大流量是唯一的,但该模型忽略了事实因素,驾驶员只关心自身的利益,包括出行时间,不愿相互协作以达到网络的最大流。因此,考虑采用双层规划模型求解网络最大流[8]。对于给定通行能力的道路,系统均衡时,整个系统的出行时间最优,即所有驾驶员的出行时间总和最小。该模型将驾驶员出行成本最小化作为路径规划的依据,可以更准确地在交通方面表征用户的行为[9],如式(6)~式(8)所示。上层问题包括将通行能力x分配到每条线路,而下层问题则是经典系统均衡模型:

式中,x满足
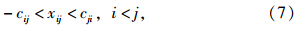

式(8)满足:
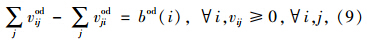
式中,cij为从i至j的通行能力;cji为从j至i的通行能力;xij为分配到道路从i至j的通行能力;vijod为OD对(i,j)的交通量;vijod为OD对的交通需求;x为动态车道的交通量分配量;tf为自由流速度;αij和βij为参数;bod(i)为每个OD节点的交通需求和供给总量;w为网络中的节点。由于这类双层规划问题难以解决,提出了一个遗传算法的解决方案[10]。
2.3.3 遗传算法求解方法遗传算法是一种启发式算法,其技术灵感来自进化生物学。遗传算法也是计算机科学人工智能领域中用于解决最优化的一种搜索启发式算法。这种启发式通常用来生成有用的解决方案来优化和搜索问题。进化算法最初是借鉴了进化生物学中的一些现象而发展起来的,这些现象包括遗传、突变、自然选择以及杂交等。遗传算法在适应度函数选择不当的情况下有可能收敛于局部最优,而不能达到全局最优[11, 12]。在方程中,基因代表了链接(i,j)所分配的交通量,适应度函数是系统均衡条件下系统的总行程时间。
3 模型验证 3.1 ILP试验采用ILP求解器来比较不同交通管理系统的网络通行效率,包括快速车道反转、低速车道反转和无车道变化的交通管理策略。在提高路网通行能力方面,假设快速车道变换的策略将比没有实现车道变换或车道变换慢的交通管理策略更优。
本文通过自动生成图的方式模拟市中心地区,图的形式为相互连接的平面网格。随机抽取3种道路类型中的1种以确定每条道路的通行能力,选取概率如表 2所示。采用随机方式选择交通发生源节点和汇聚节点。图 4所示为道路网络中两个OD交通出行量,S和T分别为交通出行量的起点和终点。
| 道路类型 | 通行能力范围/[pcu(h·车道)-1] | 概率 |
| 次干道 | 100~400 | 1 |
| 主干道 | 600~1 500 | 0.1 |
| 高速公路 | 2 400~3 200 | 0.01 |
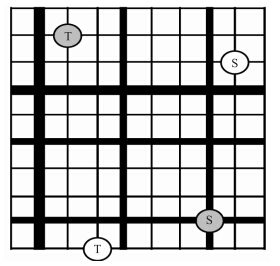
|
| 图 4 道路网络 Fig. 4 Road network |
为了评估动态可变车道策略实施与交通网络性能的关系,本研究对每种交通策略进行了10 h的测试。每小时随机产生一组新的交通流,交通管理者根据交通状况改变车道的方向。但是,并不是所有的交通管理者每小时都能反转车道,不同的交通管理系统重新配置车道所需的时间不一致。例如,某交通系统配置时间间隔为2 h,交通管理者可以每2 h 重新配置车道方向。如果交通管理者在给定的时间内无法重新配置车道对,该网络交通流分配将按照当前车道配置来求解网络最大流。如果交通管理者在给定的时间内能够重新配置车道,则计算网络完全无向边的最大交通流。
实例运行过程如下:首先,随机生成试验路网,网络配置成平衡的方式,每条道路的通行能力均衡地分配到两个方向上。接着随机生成交通流,ILP求解器计算网络通行能力,包括车道定向配置(如果交通管理者不能重新配置车道)和无方向配置(如果管理员可以重新配置车道)的道路通行能力。任何车道方向的变化将延续到下一小时新交通流的产生。
试验中评估了100个(10 km×10 km)网格,评估时间为10 h,每小时随机产生4组交通流。每个步长内评价交通管理者制订的交通管理策略下的道路通行能力,在给定的配置时间内,交通管理者所实现的总通行能力是10 h所实现的道路交通通行能力的总和。在34种不同的交通网络中经过340次试验评价了交通管理者的表现。
图 5显示了交通管理者在不同的车道配置时间下网络通行能力的状况。结果表明,相比于没有重新配置的车道,经过一定程度的重新配置车道,网络的通行能力有显著提高,同时进一步证实了网络通行能力的提升是由高频率的车道变换实现的,而非低频率的车道变换(重新配置周期=3,4,5步长)。低频率的车道变换测试结果显示该种模式下路网只能提高约12%道路通行能力。然而,当配置间隔减少到2个步长时,网络通行能力有33 %的提升。最后,在完全动态车道情况下(重新配置间隔为1),网络通行能力增长72 %。这种趋势表明,快速适应交通流情况的动态车道变换技术可有效提升交通网络的通行能力。
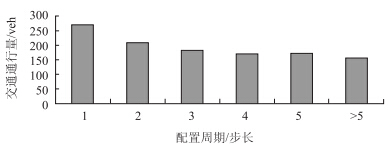
|
| 图 5 不同的车道配置时间下路网通行能力 Fig. 5 Road network capacity in different lane setting time |
本节讨论双层规划模型的实施结果。采用10 km×10 km方格网解决问题,网络中每条线路车道数量不同,通行能力均为1 800 pcu/(h·车道),α=0.1,β=0.4,tf由可用车道确定,包括30,45,70 km/h共3种速度。对于遗传算法,样本大小和生成数均设定为30,变异概率设定为0.002,交叉概率设定为0.75 。
基于以上参数,测试了10个不同时间间隔下模型的网络效能。每个间隔后得到车道配置结果以比较遗传算法和ILP求解器模型的性能,并计算遗传算法和ILP求解器解向量的相关系数。10个不同时间间隔车道配置的相关系数见表 3。结果显示,两个解向量有很大的不同。这也符合论文提出的假设,驾驶员的路径选择将导致显著不同的交通管理策略。
| 时间间隔 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 相关系数 | 0.1 | 0.2 | 0.1 | 0.3 | -0.1 | 0.3 | 0.3 | 0.3 | 0.6 | 0.1 |
由于基于网格的网络拓扑结构是高度冗余的,驾驶员出行可能有多个不同的路径。因此可以推测,两种模型的差异源于同一出行需求具有不同的路径规划方案。尽管这两种模型在约束条件下都是有效的,但是双层规划模型更能反映实际的交通网络,因为双层规划模型整合了实时交通因素,包括拥堵和速度限制等;而且双层规划模型只有近似解,而ILP求解器计算最优解。
4 结论本文提出了动态可变车道策略实现的框架。根据交通流传感器的数据的自动响应,车道方向迅速更新。随着车联网技术的发展,未来汽车将成为实现动态可变车道的关键,它将最大程度地消除人为错误。在该理论条件下,本文研究可变车道对路网通行能力的影响。试验结果表明,可变车道对提供道路和交叉口的通行能力具有积极的作用。接着,将路网的可变车道设置问题转为多物流问题,并通过整数线性规划求解每个车道的最优方向。可变车道将有助于网络效能的提升,动态(快节奏)可变车道在网络效能提升方面远大于慢节奏的可变车道策略。同时,提出了双层规划模型模拟交通拥堵和用户均衡的情景,并与遗传算法对解决多物流问题的结果进行了对比。下一步的研究方向包括设计车辆和交叉口控制方法以适应动态可变车道,以及动态变道对驾驶员行为影响的分析。
| [1] | 崔妍,刘东.北京市朝阳路可变车道交通组织研究[J].道路交通与安全,2006,6(9):21-24. CUI Yan, LIU Dong. Study on Reversible Lane Traffic Organization in Chaoyang Road of Beijing [J]. Road Traffic and Safety, 2006,6(9):21-24. |
| [2] | 孙刚,王丰元.可变车道技术对提高交通高峰时段交通流量的研究[J].科技资讯, 2006(25):176-177. SUN Gang, WANG Feng-yuan. Study on Reversible Lane for Improvement of Traffic Capacity at Peak Hour [J]. Science & Technology Information, 2006(25): 176-177. |
| [3] | CAUDILL R J. KUO N M. Development of an Interactive Planning Model for Contraflow Lane Evaluation[J]. Transportation Research Record, 1983,906:47-54. |
| [4] | 陈坚,霍娅敏.典型潮汐车流路段可变车道设置方案研究[J].重庆交通大学学报:自然科学版,2008,27(6):1127-1130. CHEN Jian, HUO Ya-min. Study on Setting Design of Variable Lane on Typical Tide Traffic Road [J]. Journal of Chongqing Jiaotong University: Natural Science Edition, 2008,27(6): 1127-1130. |
| [5] | UKKUSURI S V, WALLER S T. Linear Programming Models for the User and System Optimal Dynamic Network Design Problem: Formulations, Comparisons and Extensions[J]. |
| [6] | 张好智,高自友.可变车道的道路交通网络设计优化方法[J].中国管理科学,2007,15(2): 86-90. ZHANG Hao-zhi, GAO Zi-you. Optimization Approach for Traffic Road Network Design Problem [J]. Chinese Journal of Management Science, 2007,15(2):86-90. |
| [7] | KIM S, SHEKHAR S, MIN M. Contraflow Transportation Network Reconfiguration for Evacuation Route Planning[J]. |
| [8] | 四兵锋,赵小梅.ATIS条件下的城市交通网络系统优化模型及算法[J].系统工程学报, 2006,21(2):150-157. SI Bing-feng, ZHAO Xiao-mei. Model and Its Algorithm for System Optimization in Traffic Network under ATIS [J]. Journal of Systems Engineering, 2006, 21(2):150-157. |
| [9] | ADELI H, KUMARS. Distributed Genetic Algorithm for Structural Optimization[J]. |
| [10] | WANG Xiao-lei, YANG Hai, ZHU Dao-li. Tradable Travel Credits for Congestion Management with Heterogeneous Users[J]. |
| [11] | YANG Hai, WANG Xiao-lei. Managing Network Mobility with Tradable Credits[J]. |
| [12] | WANG Guang-min, GAO Zi-you, XU Meng. Models and a Relaxation Algorithm for Continuous Network Design Problem with a Tradable Credit Scheme and Equity Constraints[J]. |
 2015, Vol. 32
2015, Vol. 32
