扩展功能
文章信息
- 刘雄, 钟新谷, 熊先兰, 彭政
- LIU Xiong, ZHONG Xin-gu, XIONG Xian-lan, PENG Zheng
- 基于无应力状态控制法的斜拉桥运营期调索计算方法研究
- Study of Cable Adjustment Calculation Method of Cable-stayed Bridge during Operation Period Based on Control Method of Unstressed State
- 公路交通科技, 2015, Vol. 32 (9): 80-86
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 32 (9): 80-86
- 10.3969/j.issn.1002-0268.2015.09.013
-
文章历史
- 收稿日期: 2014-10-24
2. 湖南科技大学, 湖南 湘潭 411201;
3. 湘潭大学, 湖南 湘潭 411105
2. Hunan University of Science and Technology, Xiangtan Hunan 411201, China;
3. Xiangtan University, Xiangtan Hunan 411105, China
斜拉桥运营期调索施工过程是结构的内力、线形动态变化的过程,调索各施工阶段索力调整量的确定,是实现预期合理目标状态及影响运营期调索施工过程结构安全的关键性因素。
对于新建斜拉桥,成桥刚度、无应力长度及曲率等参数符合设计要求,索力调整量能通过结合影响矩阵的正装迭代法、无应力状态控制法、影响线法等方法确定。而对于运营多年的斜拉桥,受混凝土收缩徐变、拉索的松弛等因素的影响,其刚度、无应力长度及曲率偏离原来的设计,此时需先识别斜拉桥运营期刚度、无应力长度及曲率,方可通过以上方法确定索力调整量。这时,当预期合理目标索力已知,如何识别出运营多年斜拉桥的刚度、无应力长度及曲率等参数是斜拉桥运营期调索计算的核心。
在正确识别出运营多年斜拉桥的结构参数后,如何计算索力调整量和确定合理调索顺序使桥梁既满足合理恒载状态的内力状态和几何线形,又确保调索施工过程结构安全,是斜拉桥运营期调索的关键技术环节。
本文首先利用通用有限元程序ANSYS的优化功能模块识别出结构刚度参数和拉索无应力长度,然后基于无应力状态控制法,求出索力调整量。
本文以某座采用运营期调索施工的斜拉桥为背景,研究利用无应力状态控制法求解斜拉桥运营期调索施工索力调整量的方法。
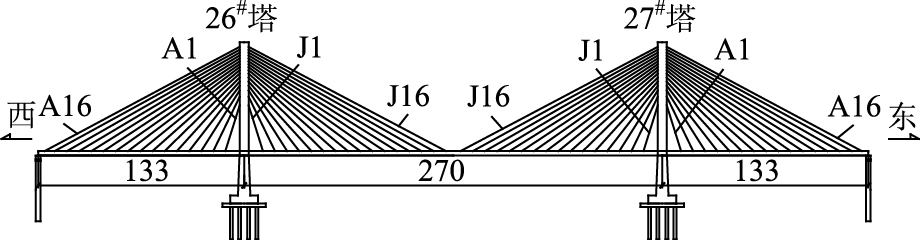
1 工程概况湘潭三桥位于湖南省湘潭市,是一座跨越湘江的城市桥梁。该桥主桥为双塔双索面预应力混凝土斜拉桥,采用塔墩固结和塔梁分离的半漂浮体系,跨径组合为(133 + 270 + 133) m,桥梁全长536 m。主梁为实心混凝土双主梁,π形横截面形式,梁高2.2 m,纵向横梁间距为4 m,桥面全宽24 m。主塔为双柱花瓶形,塔高97.3 m,塔的横截面形式为箱形截面。斜拉索在主梁上的纵向锚固间距为8 m,横向间距为18.5 m,塔上锚固间距为1.6~2.5 m。斜拉索为PES7型规格,Φ7平行镀锌钢丝。斜拉索呈扇形布置,每个塔扇形索面有16对索,分为江侧索、岸侧索,分别用字母J和A表示,1#索为最短索,16#索为最长索,每个索号对应上、下游各两根拉索,拉索编号如图 1所示。
|
| 图 1 湘潭湘江三大桥总体布置图(单位:m) Fig. 1 Layout of Xiangtan Xiangjiang third bridge(unit:m) |
设计荷载等级为汽-超20,挂车-120,人群荷载3.5 kN/m2。其立面图布置如图 1所示。
2 调索前桥梁结构状况评估调索前对湘潭三大桥进行了全面检测,包括桥梁外观检查和斜拉索索力、主梁应力、桥面线形、主塔偏位的测量等,桥梁结构状况评估如下:
(1) 主桥拉索的部分索力不正常,上、下游或者两个墩对称部分的索力不均衡,部分索力变化较大;
(2) 主桥主梁应力变化仍处于安全范围内,但主跨下缘压应力储备减少;
(3) 主桥主梁标高变化基本处于正常范围内,中跨跨中下挠10 cm以上;
(4) 两主塔塔顶均发生向江侧偏位近6 cm。
以上基本情况表明,结构总体状况良好,工作基本正常,但存在局部病害,且主塔、主梁均处于不利受力状态。为改善桥面线形和梁、塔受力状态,决定对全桥索力进行调整。
3 无应力状态控制法运营期调索计算原理根据对力学平衡方程简单的推导可以得到无应力状态法的原理: 结构单元的内力和位移随着结构的加载、体系转换和斜拉索的张拉而变化,单元的无应力长度只有人为地调整才会发生变化,当荷载和结构体系一定时,单元的无应力长度的变化必然唯一地对应一个单元轴力的变化[1]。
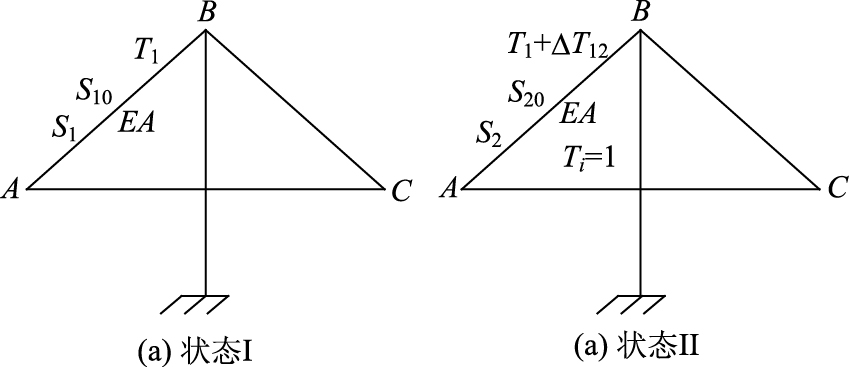
在斜拉桥结构状态I中:假设斜拉索的弹性模量为E,斜拉索截面面积为A,斜拉索的有应力长度为S1,斜拉索的无应力长度为S10,通过千斤顶施加索力T1;在斜拉桥结构状态II中:张拉后的斜拉索的有应力长度为S2,无应力长度为S20,索力为T2=T1+ΔT12。
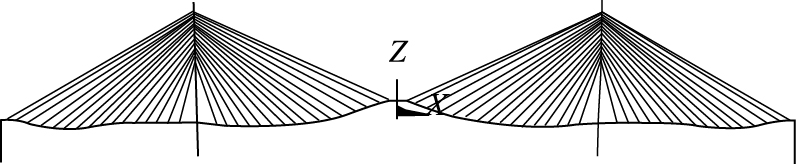
如图 2所示,当斜拉桥结构外荷载和结构体系不变时,状态I和状态II相减得到索力变化量ΔTl,它与斜拉索的无应力长度差(S20-S10)存在一一对应的关系。
|
| 图 2 斜拉桥结构状态 Fig. 2 State of cable-stayed bridge |
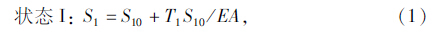
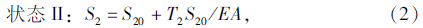
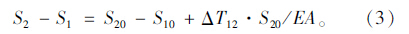
如果沿AB方向在A、B两点施加一对反向单位力,则A、B两点沿AB方向的变形设置为ε,则:
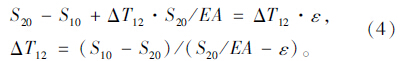
由式(4)可知:斜拉索AB的无应力长度从S10调整至S20引起的整个结构的效应,与斜拉索AB的张拉力增加ΔT12引起的整个结构的效应相同[2]。
4 运营期调索计算方法 4.1 建立结构模型和参数识别运营期斜拉桥索力优化程序的核心内容为参数识别。对处于运营期的斜拉桥来说,伴随着时间的推移,由于混凝土收缩徐变和拉索疲劳、锚具松脱导致的斜拉索功能退化,混凝土和斜拉索弹性模量出现变化;同时,由于施工与设计存在的偏差,从而引起主梁混凝土的重度出现偏差,本文根据经验选取敏感性强的参数作为待识别参数。
由于混凝土收缩徐变、温度、拉索钢丝松弛和其他环境因素影响,结构无应力状态量(无应力长度及曲率参数)已经和设计时结构的无应力状态量不同,即不是同一个结构了。因此,本文建模时,以结构调索前实测线形为基准确定并分析模型中各控制单元的坐标,其他单元的坐标由实测高程内插而得,这样就使得调索前模型的线形与结构的实际线形相一致,通过这种方式识别运营期结构发生变化的斜拉桥的主梁和索塔无应力长度及曲率参数。因此,本文模型计算根据经验仅选取拉索无应力长度和刚度参数进行识别,主要包括拉索无应力长度和主梁、索塔的弹性模量、重度[3]。
本文进行运营期斜拉桥参数识别的过程归纳如下。
(1) 建立参数化的ANSYS有限元模型,生成优化分析所需文件。
通过建立运营期斜拉桥调索初始有限元模型完成对结构系统的描述:采用beam44梁单元和shell63壳单元模拟桥面系,beam4梁单元模拟索塔,Link10杆单元模拟斜拉索。 对于塔梁间的连接,塔梁纵桥向通过设置相应的阻尼单元(Combin14)进行连接,设置刚度很大的弹簧单元联系来实现全桥的半漂浮体系;塔梁横桥向和竖桥向连接采用位移主从的方式进行;主梁两端受到桥墩的竖向和侧向约束,纵桥向相对自由,主桥和引桥间的伸缩缝仍采用弹簧单元模拟[4, 5, 6]。利用通用有限元程序ANSYS的APDL参数化语言建立的湘潭三桥主桥有限元模型如图 3所示。
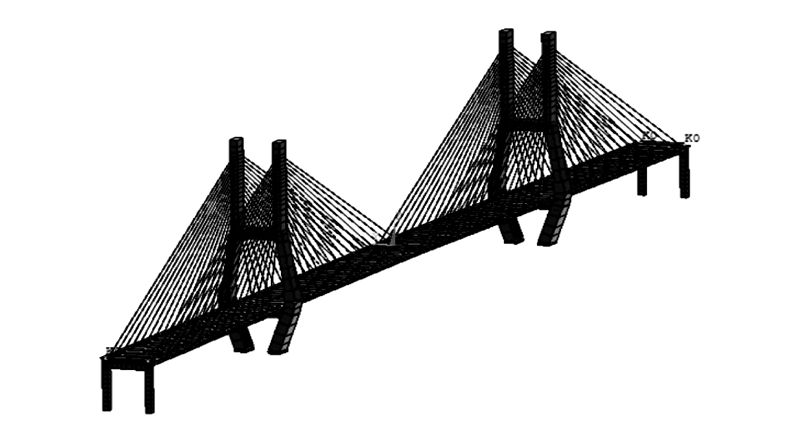
|
| 图 3 斜拉桥有限元模型图 Fig. 3 FE model of cable-stayed bridge |
(2) 基于ANSYS的优化设计功能模块,在依据经验选取的基础上,提出一种工程上易于应用的模型参数识别方法。模型参数识别的过程实际上可以看作是一个给定设计空间的有约束优化问题。经过在一定范围内的模型参数优化调整,如果计算模型各索组的索力与调索前实测索力接近乃至吻合,实现结构最终的内力和线形与实测值误差最小化的目标,获得仿真程度高的基准有限元模型并准确识别出运营期斜拉桥的刚度和拉索无应力长度。具体过程为:
①根据模型特点,将可能造成理论挠度误差的拉索无应力长度、弹性模量、重度定义为初始设计变量,记为D=[x1,x2,…,xn]。由于ANSYS未直接提供输入斜拉索初始索力(或成桥索力)的方法,斜拉索的索力是通过指定初应变实现,初应变采用胡克定律计算,即ε=Δl/l,式中Δl为拉索有应力长度扣除无应力长度的伸长量,l为拉索有应力长度。调索前基准状态有应力长度的初赋值通过计算结构实测线形得到;弹性模量、重度参数的取值上下限应在实际工程误差允许的范围内,保证修正结果物理意义的正确性。在优化分析之前应分析设计变量之间的关系,对相关设计变量进行组合,确保各设计变量为独立变量(编号相同的上、下游2根拉索无应力长度认为相等)。
②指定计算索力和主梁挠度为状态变量,记为U,V,索力控制值为U=[U1,U2,…,Um],主梁挠度值为V=[V1,V2,…,Vm]。对状态变量的约束条件不宜太小,可根据优化迭代的收敛难易程度和优化结果合理性进行确定。
③定义目标函数为主梁和索塔的弯曲应变能。
目标函数为:
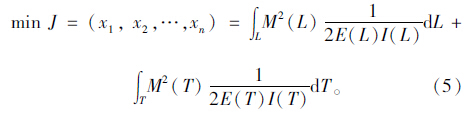
④选择合适的优化方法进行优化分析,查看优化结果。出于对优化精度的考虑,使用综合优化方法对优化结果的最优性进行验证。
综合优化方法是由ANSYS程序所提供的一系列分析-评估-修正的循环过程,即对于初始设计进行分析,对分析结果就设计要求进行评估,然后修正设计。这一循环过程重复进行,直到所有的设计要求都满足为止。它综合随机优化、零阶优化和一阶优化3种优化方法的优点,随机搜索法可以获取大量的设计变量序列;零阶方法比较容易收敛于全局最优解,收敛的速度也比较快;一阶方法的精度比较高。因此,综合优化后的结果是全局意义上的精确优化解[7, 8, 9]。
结构参数识别结果如表 1、表 2所示。
| 项目 | 弹性模量/MPa | 重度/(kN·m-3) |
| 结构部位 | 主梁、索塔 | 主梁、索塔 |
| 设计值 | 3.5×104 | 26 |
| 初始估值 | 3.5×104 | 26 |
| 估值区间 | [3.45×104,5.0×104] | [26, 35] |
| 估值 | 3.86×104 | 27.13 |
| 注:表中的设计值指按照相关规范规定计算取值 | ||
| 索号 | 无应力长度值 | 索号 | 无应力长度值 |
| A1 | 36.822 | J1 | 36.721 |
| A2 | 44.121 | J2 | 44.036 |
| A3 | 51.032 | J3 | 50.862 |
| A4 | 57.709 | J4 | 57.644 |
| A5 | 64.710 | J5 | 64.517 |
| A6 | 71.778 | J6 | 71.604 |
| A7 | 79.189 | J7 | 79.011 |
| A8 | 86.411 | J8 | 86.178 |
| A9 | 93.739 | J9 | 93.461 |
| A10 | 101.322 | J10 | 101.017 |
| A11 | 108.865 | J11 | 108.562 |
| A12 | 116.556 | J12 | 116.251 |
| A13 | 124.167 | J13 | 123.852 |
| A14 | 132.029 | J14 | 131.721 |
| A15 | 139.793 | J15 | 139.488 |
| A16 | 147.051 | J16 | 147.282 |
| 注:A索为边跨索,J索为主跨索 | |||
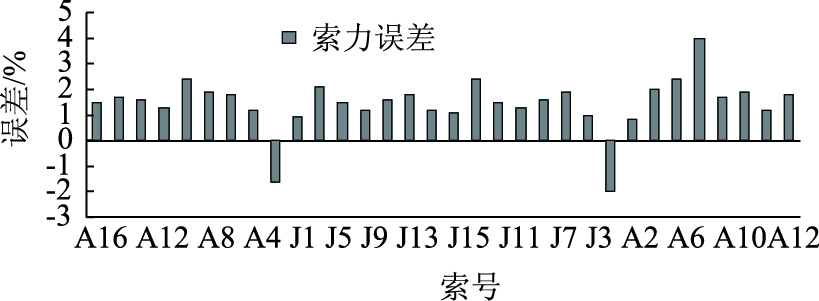
经过随机、零阶、一阶优化反复自动识别,本文模型中调索前绝大部分索力与实测索力误差在4%以内。可以认为:本文模型调索前索力与调索前实测索力吻合较好。索力误差、计算变形及线形误差分别如图 4~图 6所示。
|
| 图 4 模型参数识别后索力误差百分比图 Fig. 4 Error percentage chart of cable force after model parameter identification |
|
| 图 5 基准有限元模型计算变形(单位:N·m) Fig. 5 Calculated deformation of baseline finite element model(unit: N·m) |
|
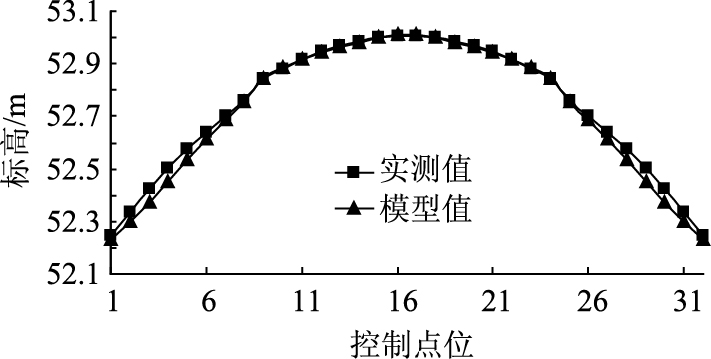
| 图 6 优化后主梁标高与实测值对比 Fig. 6 Comparison between elevation and measured value of main beam after optimization |
至此,建立起识别出调索前斜拉索无应力长度和刚度的基准有限元模型,能够仿真模拟运营期斜拉桥结构调索前基准状态的斜拉索无应力长度与结构内力、线形。
4.2 索力调整量的确定对于运营多年的斜拉桥,因主梁、索塔和斜拉索无应力长度及曲率偏离原设计的成桥状态,调索不能保证索力、主梁线形及塔偏位能同时回到成桥状态,如调索目的主要是实现塔直梁平的理想成桥状态的线形,那么目标索力不能回到成桥状态[10, 11, 12, 13]。因此,与参数识别建模过程类似,确定拉索目标索力时,在识别出真实刚度的基准有限元模型基础上,根据结构设计线形确定分析模型中各控制单元的坐标,其他相关单元的坐标由设计高程内插而得,这样就使得调索后模型的目标线形与结构的设计线形相一致,从而建立起模拟调索后目标状态的有限元模型;然后选择拉索无应力长度(编号相同的上、下游2根拉索无应力长度认为相等)为设计变量,此时斜拉索的初应变采用4.1节识别出的拉索无应力长度,计算其初赋值。主梁、索塔变形控制点位移作为状态变量,在ANSYS中主梁、索塔位移利用其后处理器来提取,其约束条件取位移的上下偏差限值为±20 mm;目标函数仍取主梁和索塔的弯曲应变能(即主梁和索塔的弯矩的平方和)来构造,其在ANSYS中进行目标拉索无应力长度确定的过程、控制命令流均与参数识别过程相类似,限于篇幅,本文不再赘述。优化出的目标拉索无应力长度值如表 3所示。
| 索号 | 无应力长度值 | 索号 | 无应力长度值 |
| A1 | 36.851 | J1 | 36.728 |
| A2 | 44.115 | J2 | 44.044 |
| A3 | 50.979 | J3 | 50.891 |
| A4 | 57.699 | J4 | 57.655 |
| A5 | 64.694 | J5 | 64.522 |
| A6 | 71.771 | J6 | 71.617 |
| A7 | 79.168 | J7 | 79.002 |
| A8 | 86.389 | J8 | 86.167 |
| A9 | 93.702 | J9 | 93.434 |
| A10 | 101.295 | J10 | 101.001 |
| A11 | 108.838 | J11 | 108.541 |
| A12 | 116.525 | J12 | 116.224 |
| A13 | 124.123 | J13 | 123.808 |
| A14 | 131.978 | J14 | 131.703 |
| A15 | 139.757 | J15 | 139.474 |
| A16 | 147.020 | J16 | 147.275 |
| 注:A索为边跨索,J索为主跨索 | |||
基于ANSYS的优化设计功能模块,在确定目标状态的斜拉索无应力长度的同时,通过后处理器得到目标索力,由式(4)知:各根斜拉索的无应力长度从调索前基准状态的无应力长度S10调整至调索后目标状态的无应力长度S20引起的整个结构的效应,与该斜拉索索力调整量ΔT12引起的整个结构的效应相同。因此,索力调整量通过无应力状态控制法得以确定,索力调整量即无应力长度的改变量,施工时可采用张拉拔出量来控制。利用ANSYS后处理器来提取目标状态与4.1节基准状态索力之差即为全桥调索的理论索力调整量,目标状态与4.1节基准状态拉索无应力长度即为相应张拉拔出量,如表 4所示。
| 索号 | 岸侧 | 江侧 | ||
| 索力调整量/kN | 张拉拔出量/mm | 索力调整量/kN | 张拉拔出量/mm | |
| 1 | -450.0 | -29.0 | -192.0 | -6.9 |
| 2 | 66 | 6.0 | -204.0 | -8.0 |
| 3 | 793 | 53.3 | -399.0 | -28.9 |
| 4 | 191 | 10.5 | -208.9 | -10.9 |
| 5 | 267 | 15.6 | -68 | -5.4 |
| 6 | 113 | 6.6 | -203.2 | -13.2 |
| 7 | 374 | 21.0 | 64.7 | 9.5 |
| 8 | 337 | 21.7 | 83.7 | 11.4 |
| 9 | 502 | 37.5 | 390.9 | 27.4 |
| 10 | 366 | 27.1 | 185.3 | 16.3 |
| 11 | 314 | 27.0 | 245.3 | 21.5 |
| 12 | 425 | 30.9 | 349.0 | 26.6 |
| 13 | 431.0 | 44.0 | 466.4 | 44.4 |
| 14 | 652.0 | 50.9 | 243.2 | 18.4 |
| 15 | 514.0 | 35.6 | 187.5 | 14.3 |
| 16 | 491.0 | 30.6 | 102.0 | 7.3 |
| 注:表中负号表示卸载或退锚,正号表示张拉或锚头拔出 | ||||
斜拉桥调索施工控制贯穿整个调索过程,不仅要保证最终调索效果达到期望,而且要确保调索过程结构安全,因此对湘潭三大桥主桥运营期调索进行了实时监测,对监测数据与理论计算进行对比分析,包括调索过程分析以及调索后结果分析。
基于以上计算方法,考虑施工方便与尽可能地缩短工期,调索按照从长索到短索、先边跨后中跨的顺序,若按照该调索顺序经计算分析,拉索、塔、梁应力均未超出容许应力,则调索过程中整个结构是安全、可靠的,该调索顺序可行。本桥运营期调索施工过程按照上述调索顺序共分为32个工况,每个工况调索完成后均对拉索、塔、梁应力进行测量,监测结果表明,每个工况的拉索、塔、梁应力均未超出容许应力,因此,本桥调索过程是安全、可靠的。由于篇幅有限,此处仅列出工况5,即调整边跨索A14调索应力变化增量如表 5所示。
| 墩号 | 应力测试断面 | 上缘应力增量 | 下缘应力增量 |
| 26#墩 | 边跨13#索 | -0.010 | -0.010 |
| 边跨1#索 | -0.119 | -0.132 | |
| 主跨1#索 | -0.148 | -0.286 | |
| 主跨13#索 | -0.390 | -0.493 | |
| 27#墩 | 主跨跨中 | 0.424 | -0.890 |
| 主跨13#索 | -0.166 | -0.217 | |
| 主跨1#索 | -0.148 | -0.183 | |
| 边跨1#索 | -0.183 | -0.390 | |
| 边跨13#索 | -0.235 | -0.126 |
| 塔号 | 左侧应力增量 | 右侧应力增量 |
| 26#塔 | -0.528 | 0.033 |
| 27#塔 | 0.933 | -0.433 |
| 注:应力增量拉为正,压为负 | ||
由表 5可以看出:塔、梁应力变化较小,全桥主梁下缘及主塔控制截面的压应力总体上均有所增加,且在合理范围之内。同时,调索监测结果表明,每个工况调索完成后梁塔线形监测结果与理论计算吻合。限于篇幅,本文不再赘述。
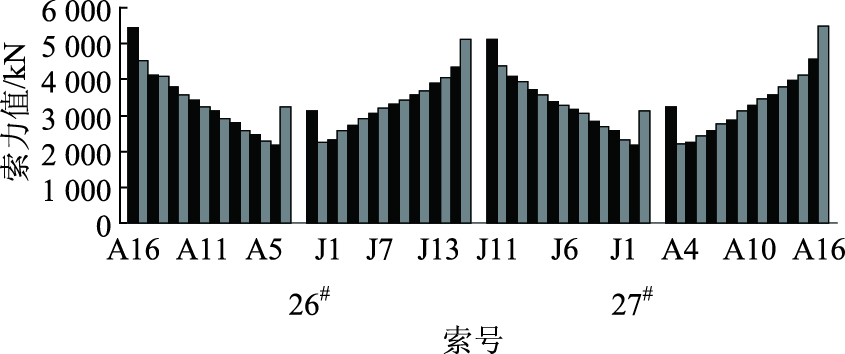
全桥调索完后全桥索力分布及其与目标索力比较情况如图 7和表 6所示(表 6中的索力值表示主梁断面同号拉索索力的平均值)。由图 7、表 6可以看出,调索后全桥索力与目标索力吻合较好,百分比偏差均在5%范围内,其中大部分小于2%,所有拉索中仅A6号拉索偏差超过3%;调索后全桥索力的均匀性得到改善,以主跨跨中为对称部分索力相差很小,索力分布更趋合理。
|
| 图 7 调索后全桥索力分布图 Fig. 7 Distribution of bridge cable forces after cable adjustment |
| 索号 | 目标索力/kN | 调索后实测索力/kN | 误差百分比/% |
| A16 | 5 414 | 5 457 | -0.42 |
| A15 | 4 543 | 4 523 | -1.38 |
| A14 | 4 149 | 4 131 | -1.28 |
| A13 | 4 019 | 4 082 | -1.01 |
| A12 | 3 777 | 3 791 | -0.53 |
| A11 | 3 536 | 3 558 | 0.21 |
| A10 | 3 423 | 3 425 | 0.15 |
| A9 | 3 259 | 3 251 | 0.73 |
| A8 | 3 120 | 3 132 | 1.64 |
| A7 | 2 905 | 2 890 | 2.08 |
| A6 | 2 799 | 2 787 | 3.02 |
| A5 | 2 639 | 2 583 | 2.20 |
| A4 | 2 522 | 2 462 | 0.99 |
| A3 | 2 305 | 2 269 | -0.48 |
| A2 | 2 241 | 2 189 | 0.51 |
| A1 | 3 179 | 3 243 | 0.52 |
| J1 | 3 102 | 3 118 | 1.99 |
| J2 | 2 225 | 2 236 | -2.31 |
| J3 | 2 318 | 2 307 | -1.56 |
| J4 | 2 539 | 2 564 | -2.37 |
| J5 | 2 672 | 2 731 | -2.14 |
| J6 | 2 829 | 2 914 | -0.43 |
| J7 | 2 987 | 3 049 | -0.53 |
| J8 | 3 155 | 3 207 | 0.39 |
| J9 | 3 301 | 3 325 | -0.26 |
| J10 | 3 406 | 3 411 | 0.05 |
| J11 | 3 556 | 3 563 | 0.63 |
| J12 | 3 705 | 3 685.5 | 0.37 |
| J13 | 3 924 | 3 884.5 | 1.57 |
| J14 | 4 115 | 4 062 | -0.45 |
| J15 | 4 400 | 4 339 | -0.44 |
| J16 | 5 144 | 5 123 | 0.80 |
通过湘潭三大桥主桥运营期调索实践可知基于无应力状态控制法,结合ANSYS优化设计的计算方法求解运营期斜拉桥索力调索量,调索后的实际状态与目标状态相比,索力误差<±3%,线形偏差<10 mm,结构内力吻合较好。目前依托工程已顺利通车,运营期调索施工过程及后运营状态桥梁工作状态良好,由此说明,斜拉桥运营期调索采用无应力状态控制法理论是可靠的,计算方法是正确的,且具有较强实用性。
本文针对运营期斜拉桥调索的具体问题基于无应力状态控制法对现有大型通用有限元软件ANSYS进行相应的二次开发,将通用软件强大的前、后处理功能以较小的成本应用于桥梁结构专业分析领域,是比较经济和切实可行的,同时通过运营期斜拉桥调索施工控制实践进行了验证,为今后类似问题的计算方法研究提供了相应的思路。
| [1] | 秦顺全.桥梁施工控制-无应力状态法理论与实践[M].北京:人民交通出版社,2007. QIN Shun-quan. Bridge Construction Control: Theory and Practice of Unstressed State Method[M]. Beijing: China Communications Press, 2007. |
| [2] | 钟继卫.斜拉桥合拢后索力最优调整的实现[J].世界桥梁, 2002(4): 43-44. ZHONG Ji-wei. Implementation of Optimal Adjustment of Cable Force of Cable-stayed Bridge after Closure[J].World Bridges, 2002(4): 43-44. |
| [3] | 姚昌荣.基于小波与分形理论的斜拉桥健康监测系统研究[D].成都:西南交通大学,2007. YAO Chang-rong. Research on Structural Health Monitoring System of Cable-stayed Bridges Based on Wavelet and Fractal Theory[D]. Chengdu:Southwest Jiaotong University,2007. |
| [4] | 任伟新,彭雪林.青洲斜拉桥的基准动力有限元模型[J].计算力学学报,2007,24(5):609-614. REN Wei-xin, PENG Xue-lin. Baseline Dynamic Finite Element Model of Qingzhou Cable-stayed Bridge[J].Chinese Journal of Computation Mechanics,2007,24(5):609-614. |
| [5] | 李宏江,王江,张永明,等. 天津永和斜拉桥换索后的索力调整[J].公路交通科技,2008, 25(10):79-83. LI Hong-jiang,WANG Jiang, ZHANG Yong-ming, et al. Cable Force Adjustment after Cable Replacement for Tianjin Yonghe Cable-stayed Bridge [J]. Journal of Highway and Transportation Research and Development, 2008, 25(10):79-83. |
| [6] | 杜蓬娟,张哲,谭素杰.斜拉桥合理成桥状态索力确定的优化方法[J].公路交通科技,2005,22(7):82-84. DU Peng-juan, ZHANG Zhe,TAN Su-jie. Optimization of Cable Tension in Reasonably Finished State of Cable-stayed Bridges[J]. Journal of Highway and Transportation Research and Development,2005,22(7):82-84. |
| [7] | 龚曙光.ANSYSY操作命令与参数化编程[M].北京:机械工业出版社,2004. GONG Shu-guang. The ANSYS Operation Command and Parameter Programming[M]. Beijing: Machinery Industry Press, 2004. |
| [8] | 孙文瑜,徐成贤,朱德通.最优化方法[M].北京:机械工业出版社, 2004. SUN Wen-yu,XU Cheng-xian,ZHU De-tong. The Optimization Method[M]. Beijing: Machinery Industry Press, 2004. |
| [9] | REID J K. On the Method of Conjugate Gradients for the Solution of Large Sparse Systems of Linear Euqations[C]// Proceedings of the Conference on Large Sparse Sets of Linear Equations. London: Academic Press, 1971:231-254. |
| [10] | 蒋伟平.斜拉桥换索理论及其技术问题的研究[D].成都:西南交通大学,2000. JIANG Wei-ping. Research on Cable Replacement Theory and Technology of Cable Stayed Bridge[D].Chengdu:Southwest Jiaotong University,2000. |
| [11] | 王美.红枫湖大桥成桥后索力调整及调索顺序的优化[D].大连:大连理工大学,2005. WANG Mei. Cable Force Adjustment and Optimization of Adjusting Sequence for Hongfenghu Bridge[D].Dalian: Dalian University of Technology,2005. |
| [12] | 朱战良.广东九江大桥换索工程研究[D].成都:西南交通大学,2003. ZHU Zhan-liang. Research on Cable Replacement of Guangdong Jiujiang Bridge[D]. Chengdu: Southwest Jiaotong University,2003. |
| [13] | 刘永刚.犍为岷江大桥换索工程计算与分析[D].成都:西南交通大学,2000. LIU Yong-gang. Calculation and Analysis of Cable Replacement Work of Qianwei Minjiang Bridge[D].Chengdu: Southwest Jiaotong University,2002. |
 2015, Vol. 32
2015, Vol. 32
