扩展功能
文章信息
- 李松辉, 徐忠燕, 蒋含莞
- LI Song-hui, XU Zhong-yan, JIANG Han-wan
- 超重车辆对公路桥梁安全性的影响
- Influence of Overweight Vehicles on Bridge Safety
- 公路交通科技, 2015, Vol. 32 (9): 74-79
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 32 (9): 74-79
- 10.3969/j.issn.1002-0268.2015.09.012
-
文章历史
- 收稿日期: 2014-12-04
2. 旧桥检测与加固技术交通行业重点实验室(北京), 北京 100088
2. Key Laboratory of Bridge Detection and Reinforcement Technology of the Ministry of Transport (Beijing), Beijing 100088, China
公路超重车辆的荷载远远超过设计荷载,严重危及公路桥梁的安全运营,是近年来导致桥梁坍塌事故频发的主要因素之一。为确保公路桥梁的安全运营,世界各国均十分重视公路超重车辆的监管工作[1, 2, 3, 4, 5]。以我国为例,为减小超载运输对交通安全、公路桥梁的危害,国家加大了超重运输治理力度,先后制订了一系列的法律、法规。《认定车辆超限超载的标准》规定了6种车辆超限超载情形,其中,前5种是针对5类不同轴数货运车辆的质量超限认定,5类货车的车货总质量限值分别为:二轴货车20 t,三轴货车30 t,四轴货车40 t,五轴货车50 t,六轴及六轴以上货车55 t等。第6种情形是针对交通安全考虑的,即车辆总质量应同时满足行驶证核定的装载质量。在上述规定中,第1~5种情形属技术层面的限载范畴,由交通管理部门负责。第6种情形属政策层面的限载范畴,由公安交警部门负责。
由于我国设计规范的变迁,不同线路甚至同一线路上桥梁的设计荷载等级也不尽相同,单一的限载模式难以有效保护桥梁的安全运营,因此,有必要系统研究超重车辆对桥梁安全性的影响程度,以便为在役桥梁限载标准的制订提供依据。
本文以钢筋混凝土中、小跨径简支梁桥抗弯承载力为例,通过引入车辆荷载影响系数,模拟不同超重车辆对桥梁安全性的影响规律,为桥梁限载标准制订、桥梁超载状态判定、超限运输管理以及加固维修决策提供依据,确保在役桥梁的安全运行。
1 安全性分析模型对于钢筋混凝土中、小跨度简支梁桥,可将结构恒载G和汽车荷载Q作为结构可靠性分析的最基本荷载组合。若恒载效应随机变量为SG,汽车荷载效应随机变量为SQ,抗力随机变量为R,则桥梁结构的功能函数可表示为
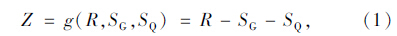
根据《公路工程结构可靠度设计统一标准》[6](以下简称《统一标准》),SG的分布类型为正态分布,抗力R服从对数正态分布,设计基准期内汽车荷载效应最大值SQ服从极值Ⅰ型分布。
在进行超重车辆安全性分析时,可引入活载影响系数ζq反映不同超重水平对汽车荷载效应的影响。根据式(1),若考虑活载影响系数后的汽车荷载效应为ζqSQ,则结构功能函数可改写为:
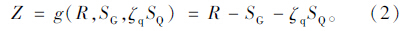
由于ζq为某一常量,则提高后的汽车荷载效应ζqSQ仍服从极值Ⅰ型,相应的均值和变异系数为:
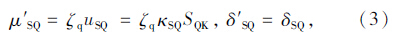
根据式(2),若给定抗力和荷载效应的统计参数,即可按可靠性理论分析超载运输对桥梁结构或构件可靠性的影响规律。
与规范校准的计算步骤类似[6, 7, 8],首先根据钢筋混凝土受弯构件承载能力极限状态设计表达式,建立受弯抗力标准值与恒载效应、汽车荷载效应的关系式。进而,采用一次二阶矩之映射变换法编程计算与不同活载影响系数ζq对应的可靠指标。最后,通过分析构件可靠指标随不同ζq变化规律,揭示超重运输对桥梁安全性的影响程度。
下面根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTJ 023—85)(以下简称85规范)[9]和JTG D62—2004桥梁设计规范(以下简称04规范)[10]钢筋混凝土受弯构件设计表达式,分析不同超载水平对桥梁安全性的影响规律。
2 计算方法由于04桥梁规范采用了以可靠性理论为基础的极限状态设计方法,而85桥梁规范属于半经验、半概率的极限状态设计方法,二者在设计理论上差异较大[9, 10],下面首先给出85规范与04规范钢筋混凝土受弯构件的设计表达式。
按85规范设计的钢筋混凝土中小跨经简支梁桥,其抗力标准值可表示为[8]:
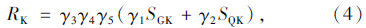
按04规范设计的桥梁,若设计安全等级为二级,则相应的抗力标准值可表示为[11, 12, 13]:
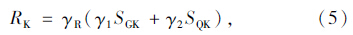
式(4)和式(5)仅给出了抗力与荷载效应标准值的关系式,进行可靠性分析时,尚需将各标准值与相应基本变量统计参数联系起来。根据《统一标准》,各基本随机变量的统计参数可采用如下形式[6]:
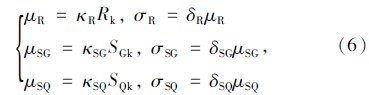
根据《统一标准》,各随机变量的分布类型与统计参数见表 1[6]。
| 变量种类 | 运行状态 | 分布类型 | 平均值/ 标准值κ |
变异系数 δSQ |
| 抗力(受弯) 恒载效应 |
— | 对数正态 | 1.226 2 | 0.141 4 |
| — | 正态 | 1.014 8 | 0.043 1 | |
| 汽车荷载效 应(弯矩) |
一般 | 极值Ⅰ型 | 0.686 1 | 0.156 9 |
| 密集 | 极值Ⅰ型 | 0.799 5 | 0.086 2 |
由式(4)和式(5)可知,若汽车荷载标准值效应与恒载标准值效应的比值(ρ=SQK/SGK)一定,恒载效应SGK或汽车荷载效应SQK的增减也将使抗力标准值Rk按同一比例增减。
进一步,若抗力与荷载效应无量纲参数的均值和变异系数等保持不变,即κR,κSG,κSQ和δR,δSG,δSQ等取恒定的值,则SGK或SQK的增减也将使抗力、恒载效应和汽车荷载效应等随机变量按同一比例增减。根据式(2),结构的可靠指标仅与设计采用的活恒载比值ρ有关,而与SGK或SQK的具体取值无关,这一处理思路也为规范可靠度校准分析所采用。超载桥梁安全性分析时,可选取活恒载比值为基本参数,从而避免涉及桥梁跨径、截面尺寸、车道数、荷载横向分布系数等具体设计参数的影响,使超载桥梁安全性分析结果更具一般性。
根据以上分析,即可按结构可靠性分析的基本方法计算与不同ζq对应的可靠指标。因式(2)中含有非正态随机变量,本文采用一次二阶矩法中的映射变换法编写了超载桥梁可靠指标计算程序,基本步骤如下[13, 14]:
(1) 给定ρ和ζq,按式(4)或(5)计算R,SG以及ζqSQ的统计参数。
(2) 按数学变换的方法将R,SG以及ζqSQ等基本随机变量转换为标准正态随机变量YR,YSG,YSQ。
(3) 给定β值,假定随机变量Yi在验算点处的初值(yR*,ySG*,ySQ*)。
(4) 求验算点处的方向余弦
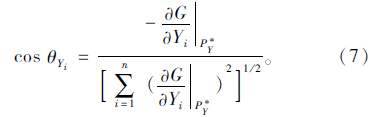
(6) 计算验算点(yR*,ySG*,ySQ*)的新值

(7) 将yi代入由标准正态随机变量YR,YSG,YSQ表示的极限状态方程
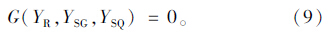
(8) 以验算点计算值(yR*,ySG*,ySQ*)为初值,重复步骤(4)~(7),直到两次计算的β值小于允许误差为止。
(9) 对于给定的ρ值,选取不同的ζq值,重复步骤(3)~(8),计算与不同ζq对应的可靠指标值。
(10) 对于每一个给定的ρ值,重复步骤(3)~(9)。
限于篇幅,本文仅以钢筋混凝土中、小跨径简支梁桥为例,分析活载影响系数ζq对受弯状态可靠指标的影响规律。
3 按85规范分析在我国已有公路桥梁中,按原85规范设计建造的桥梁占了很大的比例。经过十余年甚至数十年的运营,桥上活载状况发生了很大的变化,因此,如何合理鉴定此类桥梁的安全性是确保桥梁安全运营的重要手段。下面针对不同的活载影响系数,详细分析按原桥梁设计规范设计钢筋混凝土中小跨径桥梁的可靠指标变化规律,以揭示此类桥梁隐含的安全性水平。
公路桥梁的常遇设计活恒载比值并不失一般性,后续分析中,ρ选用0.1,0.25,0.5,1.0,1.5和2.5等6种比值参与计算。计算中涉及到的乘积γ3γ4γ5,可按85规范受弯构件抗力表达式进行推算[13]。
下面分别按汽车一般运行状态和密集运行状态计算与不同活载影响系数对应的可靠指标。其中,一般运行状态与汽车-20级桥梁对应,密集运行状态与汽车-超20级对应。为叙述方便,后面不再区分汽车运行状态与设计荷载等级。与活载影响系数对应的可靠指标计算结果见表 2。
| 运行状态 | ρ | γR | 活载影响系数ζq | ||||||||
| 1.0 | 1.05 | 1.10 | 1.15 | 1.20 | 1.25 | 1.35 | 1.45 | 1.55 | |||
| 一般 | 0.1 | 1.312 5 | 4.645 7 | 4.624 7 | 4.603 7 | 4.582 7 | 4.561 8 | 4.540 8 | 4.499 0 | 4.457 3 | 4.415 6 |
| 0.25 | 1.312 5 | 5.012 9 | 4.960 9 | 4.909 1 | 4.857 3 | 4.805 8 | 4.754 3 | 4.652 2 | 4.550 8 | 4.450 5 | |
| 0.5 | 1.287 5 | 5.188 0 | 5.087 1 | 4.988 2 | 4.891 0 | 4.796 0 | 4.702 9 | 4.522 3 | 4.349 2 | 4.183 2 | |
| 1.0 | 1.250 0 | 5.047 6 | 4.905 9 | 4.769 5 | 4.638 2 | 4.511 6 | 4.389 2 | 4.156 5 | 3.937 6 | 3.730 7 | |
| 1.5 | 1.250 0 | 4.987 0 | 4.832 1 | 4.683 9 | 4.541 6 | 4.404 9 | 4.273 1 | 4.023 2 | 3.789 0 | 3.568 3 | |
| 2.5 | 1.250 0 | 4.899 6 | 4.734 9 | 4.577 7 | 4.427 2 | 4.282 8 | 4.143 9 | 3.880 7 | 3.634 5 | 3.402 6 | |
| 密集 | 0.1 | 1.312 5 | 4.579 1 | 4.555 2 | 4.531 4 | 4.507 7 | 4.484 0 | 4.460 4 | 4.413 2 | 4.366 3 | 4.319 7 |
| 0.25 | 1.312 5 | 4.887 8 | 4.832 5 | 4.777 5 | 4.722 9 | 4.668 6 | 4.614 6 | 4.507 7 | 4.402 0 | 4.297 8 | |
| 0.5 | 1.287 5 | 5.102 4 | 5.004 1 | 4.907 2 | 4.811 4 | 4.716 9 | 4.623 7 | 4.441 1 | 4.263 4 | 4.090 4 | |
| 1.0 | 1.250 0 | 5.216 0 | 5.063 0 | 4.914 2 | 4.769 5 | 4.628 6 | 4.491 2 | 4.226 8 | 3.974 3 | 3.732 6 | |
| 1.5 | 1.250 0 | 5.294 4 | 5.117 4 | 4.946 5 | 4.781 2 | 4.620 9 | 4.465 3 | 4.167 2 | 3.884 0 | 3.613 8 | |
| 2.5 | 1.250 0 | 5.310 4 | 5.115 2 | 4.927 3 | 4.746 0 | 4.570 9 | 4.401 0 | 4.075 9 | 3.767 7 | 3.473 6 | |
根据表 2,亦可绘制与汽车一般运行状态和密集运行状态对应的β-ζq关系曲线,见图 1。
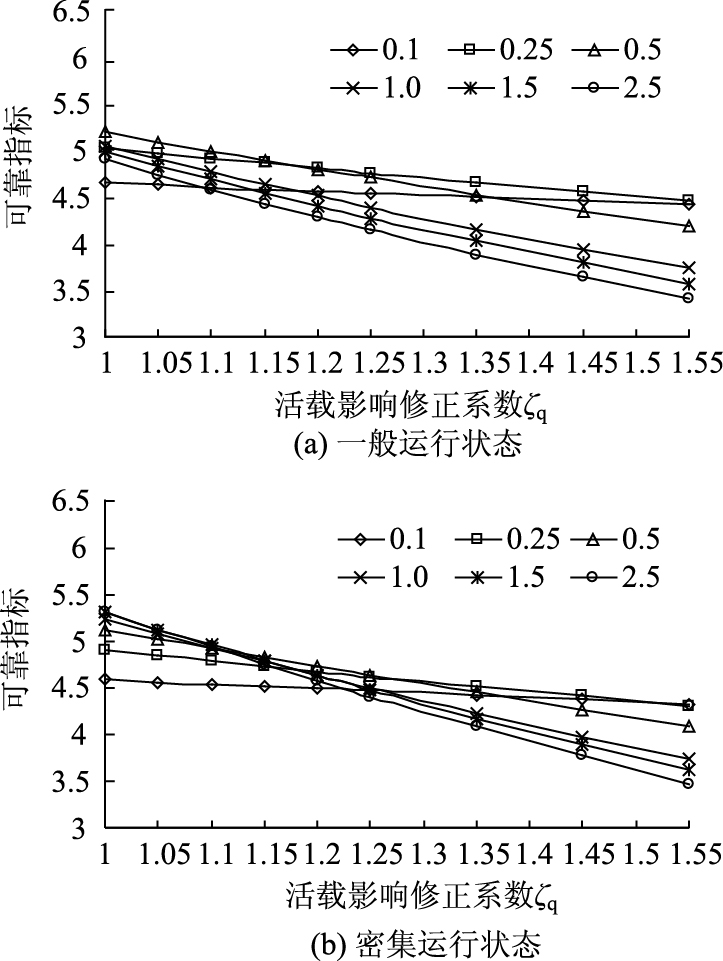
|
| 图 1 超载对受弯构件可靠性的影响规律 Fig. 1 Effect of overload on reliability of flexural members |
由表 2和图 1可知,当设计采用的活恒载比值ρ为0.1时,活载影响系数对桥梁的可靠指标影响并不明显。随着活恒载比值不断增大,活载影响系数对受弯构件可靠指标的影响程度越大。由此可见,设计采用的活恒载效应比值对超载桥梁构件的可靠性影响显著。以汽车一般运行状态为例,当设计采用的活恒载比值为0.1时,与ζq=1.0对应的可靠指标为4.645 7,与ζq=1.55对应的可靠指标为4.415 6,相应的可靠指标降低量为0.23,而在ζq取值相同的情况下,与ρ=2.5对应的可靠指标降低量则高达1.497。
进一步分析可知,若给定活载影响系数ζq,构件可靠指标随活恒载比值ρ的增加而趋于稳定。下面给出不同汽车运行状态下桥梁的β-ρ关系曲线,如图 2所示。其中,图(a)和图(b)分别与汽车一般运行状态和密集运行状态对应。
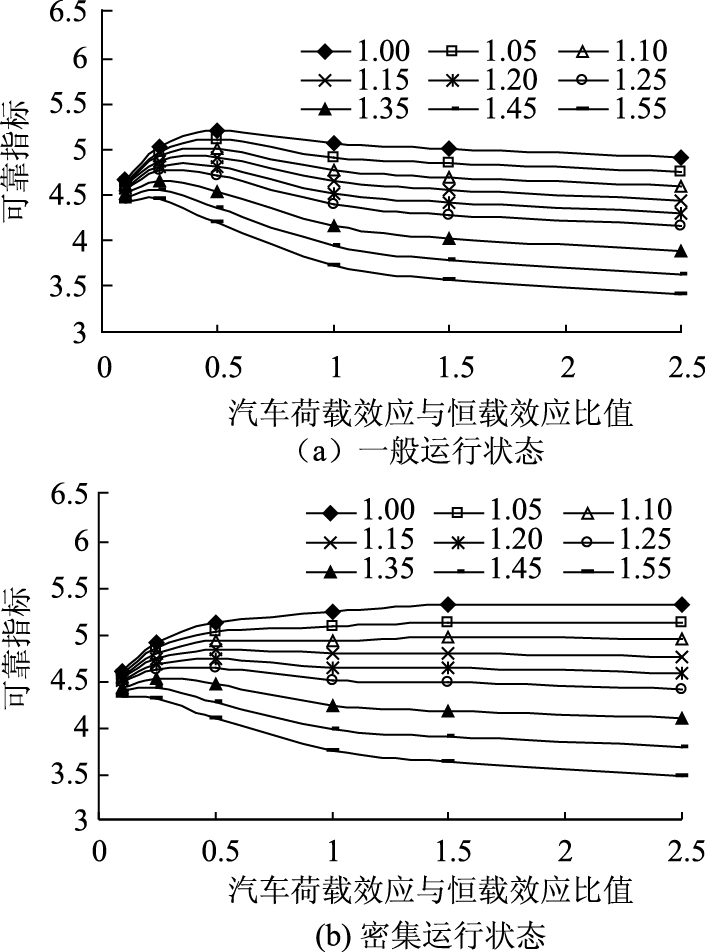
|
| 图 2 活载效应与恒载效应比值对桥梁可靠性的影响规律 Fig. 2 Effect of ratio of live load effect to dead load effect on reliability of bridges |
按04规范设计的钢筋混凝土桥梁,其受弯抗力分项系数为1.125 4[6]。由于该抗力分项系数是以目标可靠指标为基准,按最小二乘法经优化分析得到的,与不同活恒载比值对应的结构可靠指标与目标可靠指标或有差别。为分析方便,下面以设计安全等级为二级的理想抗力桥梁为例,分析活载影响系数对结构可靠指标的影响规律[13]。
以结构安全等级二级的钢筋混凝土简支梁桥为例,若设计采用的目标可靠指标为β0=4.2,且与之对应的抗力分项系数为γR,β0[13],则(5)可改写为:
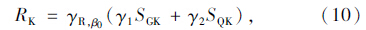
下面根据安全等级二级的理想抗力水平为基准,计算与不同活载影响系数对应的可靠指标。分析时,同样采用6种不同的活恒载比值,计算结果见表 3。
| 运行状态 | ρ | γR,β0 | 活载影响系数ζq | ||||||||
| 1.0 | 1.05 | 1.10 | 1.15 | 1.20 | 1.25 | 1.35 | 1.45 | 1.55 | |||
| 一般 | 0.1 | 1.229 7 | 4.200 | 4.178 9 | 4.157 9 | 4.137 0 | 4.116 1 | 4.095 1 | 4.053 4 | 4.011 7 | 3.970 2 |
| 0.25 | 1.164 4 | 4.200 | 4.149 2 | 4.098 4 | 4.048 0 | 3.997 7 | 3.947 7 | 3.848 4 | 3.750 3 | 3.653 3 | |
| 0.5 | 1.102 0 | 4.200 | 4.106 1 | 4.013 5 | 3.922 6 | 3.833 2 | 3.745 3 | 3.574 4 | 3.409 5 | 3.250 5 | |
| 1.0 | 1.065 0 | 4.200 | 4.062 3 | 3.929 6 | 3.801 3 | 3.677 1 | 3.556 8 | 3.326 6 | 3.108 8 | 2.901 9 | |
| 1.5 | 1.060 6 | 4.200 | 4.047 1 | 3.900 7 | 3.759 7 | 3.623 7 | 3.492 4 | 3.241 8 | 3.005 6 | 2.781 6 | |
| 2.5 | 1.064 6 | 4.200 | 4.036 3 | 3.879 7 | 3.729 2 | 3.584 4 | 3.444 7 | 3.178 6 | 2.929 7 | 2.690 3 | |
| 密集 | 0.1 | 1.241 9 | 4.200 | 4.176 3 | 4.152 4 | 4.128 6 | 4.104 9 | 4.081 2 | 4.034 0 | 3.987 0 | 3.940 3 |
| 0.25 | 1.187 5 | 4.200 | 4.145 1 | 4.090 2 | 4.035 6 | 3.981 4 | 3.927 5 | 3.820 8 | 3.715 5 | 3.611 6 | |
| 0.5 | 1.127 8 | 4.200 | 4.102 6 | 4.006 7 | 3.912 1 | 3.818 6 | 3.726 5 | 3.546 0 | 3.370 3 | 3.199 3 | |
| 1.0 | 1.067 5 | 4.200 | 4.048 8 | 3.901 8 | 3.758 4 | 3.618 6 | 3.482 0 | 3.218 0 | 2.965 3 | 2.722 9 | |
| 1.5 | 1.041 3 | 4.200 | 4.021 4 | 3.848 9 | 3.681 5 | 3.518 8 | 3.360 6 | 3.054 6 | 2.766 4 | 2.489 6 | |
| 2.5 | 1.021 2 | 4.200 | 3.999 6 | 3.805 9 | 3.618 1 | 3.435 8 | 3.258 5 | 2.917 8 | 2.593 4 | 2.283 6 | |
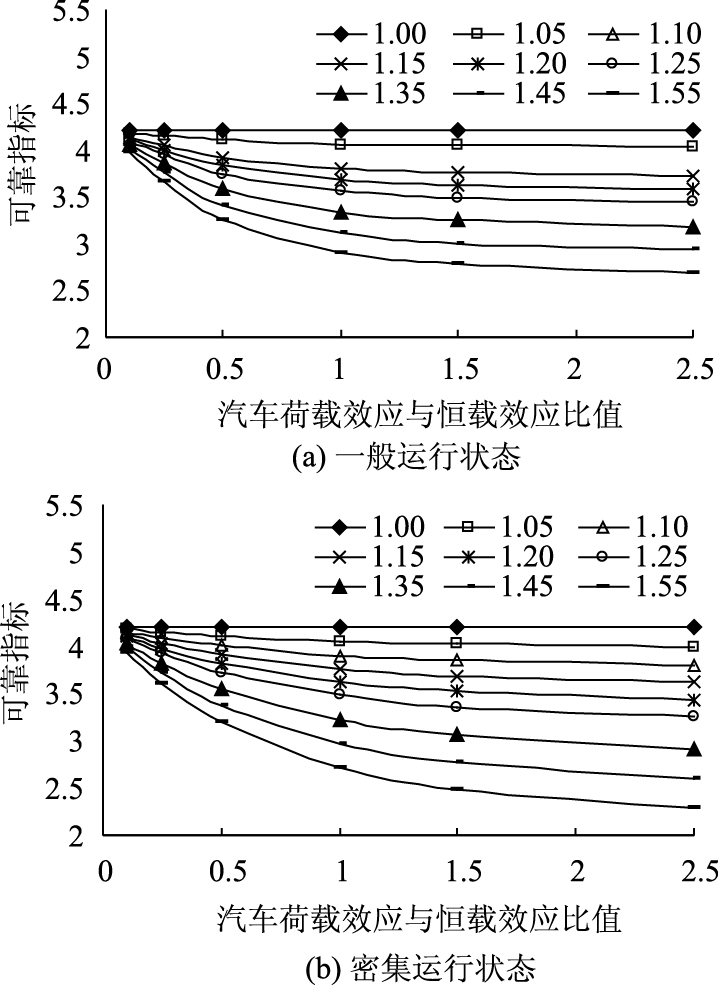
根据表 3,同样可以绘制与汽车一般运行状态和密集运行状态对应的β-ζq曲线与β-ρ曲线,见图 3和图 4。
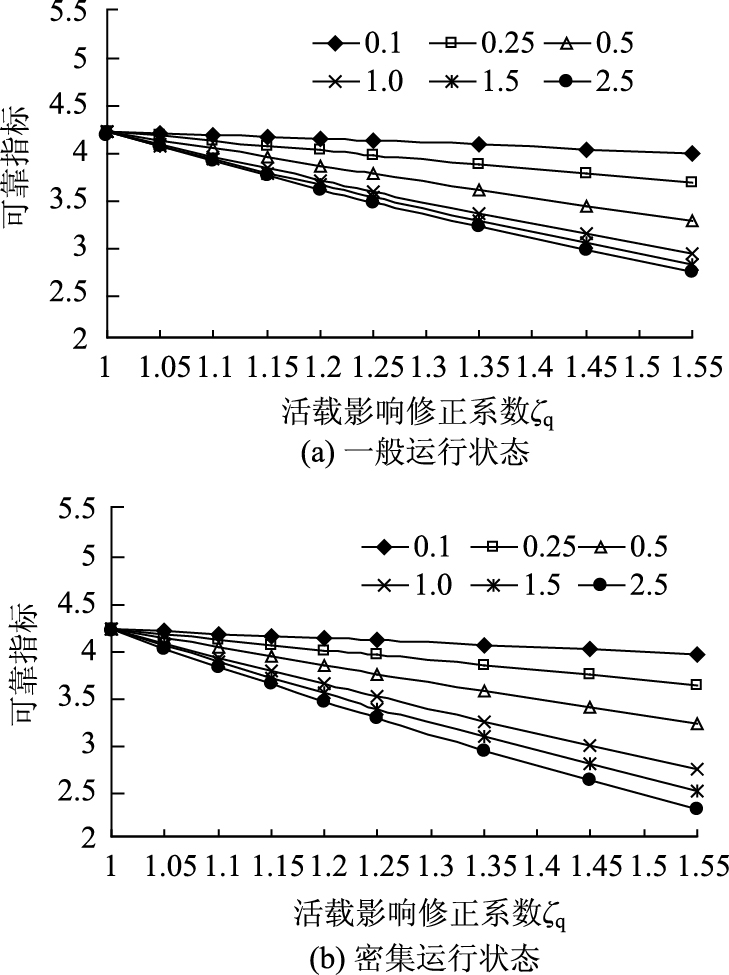
|
| 图 3 超载对受弯构件可靠指标的影响规律 Fig. 3 Effect of overload on reliability index of flexural members |
|
| 图 4 活恒载效应比值对超载桥梁可靠性的影响 Fig. 4 Effect of ratio of live load effect to dead load effect on reliability of overloaded bridges |
由图 1和图 3可知,无论是按85规范还是04规范设计的桥梁,活载影响系数ζq与可靠指标β均呈线性关系。对于相同的设计活恒载比值ρ,除初始可靠指标不同外,二者的增减幅度(直线斜率)是相同的。
进一步分析表明,在设计活恒载比值一定的情况下,抗力分项系数γR与结构可靠指标β同样呈线性关系。因此,若已知γR与γR,β0的值,表 2亦可由表 3按线性内插或外推的方法得到。
5 结论通过引入汽车荷载影响系数,系统分析了不同汽车荷载水平对85规范桥梁和04规范理想抗力桥梁可靠指标的影响规律,经分析,可以得出以下结论:
(1) 随着超载系数的增加,结构可靠指标与活载影响系数呈近似线性关系,并且ρ越大,可靠指标的降低幅度越大,即设计采用的汽车荷载效应所占比例越大,桥梁的相对抗超载能力越差,反之越强。
(2) 若活载影响系数一定,随着活恒载比值的增加,可靠指标的降低幅度减小,超载对桥梁结构可靠性的影响趋于稳定。
(3) 按原85规范设计的桥梁受弯构件,其隐含的可靠指标一般均高于安全等级二级下的目标可靠指标,在该安全等级下,桥梁结构可承受一定的超重车辆作用。对于设计活恒载比值为1.0的钢筋混凝土梁桥,可承受高于设计汽车荷载25%~35%的超载作用。
| [1] | 蔡建华,张剑飞. 超限运输的成因及治理对策[J]. 中国公路学报,2006,19(3):100-105. CAI Jian-hua,ZHANG Jian-fei. Cause of Overweight Transportation and Administration Countermeasure[J]. China Journal of Highway and Transport, 2006,19(3):100-105. |
| [2] | FU G K, FU C. Bridge Rating Practices and Policies for Overweight Vehicles, NCHRP Synthesis 359 [R]. Detroit: Wayne State University,2006. |
| [3] | HONEFANGER J, STRAWHORN J, ATHEY R, et al. Commercial Motor Vehicle Size and Weight Enforcement in Europe [R]. Washington, D.C.: U.S. Department of Transportation, 2007. |
| [4] | ZHOU Xiang. Structural and Economical Impacts of Heavy Truck Loads on Bridges [D]. Louisiana: Louisiana Tech University, 2007. |
| [5] | SCHULMAN J F. Heavy Truck Weight and Dimension Limits in Canada [R]. Ottawa: The Railway Association of Canada, 2003. |
| [6] | GB/T 50283—1999,公路工程结构可靠度设计统一标准 [S]. GB/T 50283—1999,Unified Standard for Reliability Design of Highway Engineering Structures [S]. |
| [7] | MOSES F. Calibration of Load Factors for LRFR Bridge Evaluation, NCFRP Report 454 [R]. Pittsburgh: University of Pittsburgh, 2001. |
| [8] | GAYTON N,MOHAMED A,SORENSEN J D,et al. Calibration Method for Reliability-based Design Codes [J]. Structural Safety, 2004(26):91-121. |
| [9] | JTJ 023—85,公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTJ 023—85, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culvers [S]. |
| [10] | JTG D62—2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG D62—2004, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts [S]. |
| [11] | 李松辉. 基于车辆荷载效应截尾分布的桥梁限载分析方法[J]. 工程力学,2014,31(2):117-124. LI Song-hui. Analytical Approach for Determining Truck Weight Limits with Truncated Distributions of Live Load Effect on Highway Bridges [J]. Engineering Mechanics, 2014,31(2):117-124. |
| [12] | 李松辉. 公路桥梁限载取值的可靠性分析模型研究 [J]. 土木工程学报,2013,46(9):83-90. LI Song-hui. Reliability-based Analytical Model for Determining the Truck Weight Limits on Highway Bridges [J]. China Civil Engineering Journal, 2013, 46(9):83-90. |
| [13] | 王松根,李松辉. 公路桥梁限载标准的可靠性分析方法[J]. 工程力学,2010,27(10):162-166. WANG Song-gen, LI Song-hui. Reliability-based Analysis on the Vehicle Weight Limit of Highway Bridges [J]. Engineering Mechanics, 2010,27(10):162-166. |
| [14] | 赵国藩,金伟良,贡金鑫. 结构可靠度理论 [M]. 北京:中国建筑工业出版社,2000. ZHAO Guo-fan, JIN Wei-liang, GONG Jin-xin. Structural Reliability Theory[M]. Beijing: China Architecture & Building Press, 2000. |
 2015, Vol. 32
2015, Vol. 32
