扩展功能
文章信息
- 江辉, 杨朔, 王宝喜, 杨庆山, 曾亚光
- JIANG Hui, YANG Shuo, WANG Bao-xi, YANG Qing-shan, ZENG Ya-guang
- 近、远场强震下RC连续梁桥损伤及滞回耗能特性对比研究
- Comparative Study of Damage and Hysteretic Energy Characteristics of RC Continuous Girder Bridge Caused by Near-field and Far-field Strong Earthquake
- 公路交通科技, 2015, Vol. 32 (9): 64-73
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 32 (9): 64-73
- 10.3969/j.issn.1002-0268.2015.09.011
-
文章历史
- 收稿日期: 2014-08-18
2. 圣母大学 土木与环境工程及地球科学系, 美国 南本德 46556
2. Department of Civil & Environmental Engineering & Earth Science, University of Notre Dame, South Bend 46556, USA
基于性能的结构抗震设计是抗震设计理论发展的必然趋势,在美国ATC-40[1]、FEMA-350[2]、FEMA-356[3]和我国《建筑工程抗震性态设计通则》[4]等报告、标准中得到体现。其主要内容包括,地震设防标准的确定、抗震性能水准的划分、抗震性能目标的确定以及基于性能的抗震设计方法等几个方面。这一理论使得抗震设防由传统的以生命安全为单一目标转为综合考虑生命安全与财产损失的多个层次的目标体系[5, 6, 7]。马宏旺,吕西林[5]系统阐述了基于性能的结构抗震设计与现行抗震设计思想的区别和联系。地震下的结构变形及能量耗散是性能抗震设计中应综合考虑的两个重要的因素[8, 9, 10, 11]。文献[8]提出了同时考虑变形和能量需求的基于性能的强度折减因子;文献[9]、[10]分别讨论了桥梁和建筑框架结构基于性能的抗震设计方法;文献[11]揭示了RC桥墩的地震动损伤及滞回耗能特性。因此,在基于性能的桥梁结构抗震设计中,强震下的结构损伤、滞回耗能及其分布特征,是基于性能抗震设计的重要内容,有必要以桥梁结构全桥模型为对象,开展相关研究。
近20 a发生的几次主要地震,如1994年美国Northridge地震、1995年日本Kobe地震、1999年我国台湾Chi-Chi地震、2008年我国汶川地震等的震害均主要集中在近断层区域。相对于远场地震而言,近断层地震动(也称近场地震)具有断层破裂的强方向性效应(forward rupture directivity)、滑冲效应(fling step)、上盘效应以及大幅值竖向加速度特性等显著区别于远场区的地震地面运动特征[12, 13, 14],其中近场地震下的大幅值、长周期脉冲作用是重要的表现形式之一,导致地震能量以递增的形式进行,难以在短时间内耗散,对建筑物及桥梁结构造成更加严重的破坏,已引起了地震工程界的广泛关注。Jonsson [15]、王东升 [16]、Brown和Saiidi [17]的研究均表明,近断层地震下的结构震害显著区别于远场。因此,有必要从桥梁结构能量和损伤分布特征的角度,对比分析其在近、远场地震激励下的差异,为不同类型地震下基于性能的抗震设计奠定基础。
本文在传统的强震下结构分析以强度和变形为主的基础上,考虑累积耗能效应,引入改进的Park-Ang双参数损伤评估指标[8],以典型的高速公路双柱式RC连续梁桥为对象,建立可考虑桥墩非线性力学行为的全桥有限元数值模型,挑选典型近断层和远场强震记录,采用非线性时程积分方法并自编程序计算能量等指标,对比分析了近、远场两类地震下频谱、峰值加速度(PGA)、持时等要素对滞回耗能、结构损伤量值及其分布的影响规律。
1 算例桥梁及其模拟模型 1.1 桥梁概况选取某三跨双柱式RC连续梁桥为对象,上部结构为3×16 m预应力混凝土空心板梁;双柱式桥墩,两柱间间距9.25 m,墩身为圆形截面,直径1.5 m,1#、2#桥墩高度分别为11.175 m和15.039 m;梁体与下部结构之间通过板式橡胶支座连接,0#、3#桥台和1#、2#墩顶分别设置四氟乙烯GYZF4板式橡胶支座和普通GYZ板式橡胶支座。上部结构和墩身分别采用C50、C30混凝土,墩柱纵向钢筋采用28根直径28 mm的HRB335钢筋,箍筋采用直径为10 mm的R235钢筋,间距为100 mm。限于篇幅,全桥及支座布置见文献[18]。
1.2 桥墩非线性单元参数分析由于水平地震作用下梁体主要做刚体平动和转动,以动能的方式耗散地震能量,除阻尼耗能外,弹塑性地震行为主要集中于墩身(为了突出研究重点,本文依照通常办法对板式支座按弹性力学行为考虑)并产生滞回耗能,因此本文通过沿桥墩高度设置弹塑性梁单元来考虑其可能的弹塑性力学行为。延性是表征结构变形和滞回耗能能力的重要指标,为了准确计算各桥墩不同部位的延性变形能力,对1#、2#桥墩进行了不同截面的弯矩-曲率(M-φ)分析,以确定弹塑性梁单元的屈服点、极限点参数。各桥墩截面纵筋布置如图 1所示,利用XTRACT软件对桥墩不同高度截面进行M-φ分析,所得到的2#墩墩底截面滞回骨架曲线如图 2所示,通过等效线性化可得到其屈服点和极限点参数。1#、2#墩墩顶、墩底截面的曲率延性及弯矩指标见表 1。各桥墩不同截面的等效塑性单元长度依据《公路桥梁抗震设计细则》计算确定[19],计算得1#、2#桥墩的塑性铰长度为100 cm,故1#墩每柱可划分为11个梁单元,2#墩每柱可划分为15个梁单元。
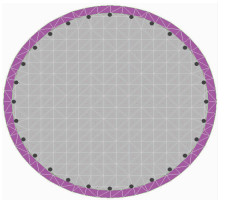 |
| 图 1 桥墩截面纵筋布置 Fig. 1 Arrangement of longitudinal bars in piers |
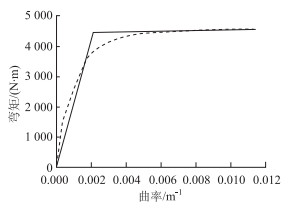 |
| 图 2 2#桥墩墩底截面弯矩-曲率关系 Fig. 2 Moment-curvature relation of bottom section of 2nd pier |
| 墩号/位置 | 屈服曲率/(×10-3·m-1) | 极限曲率/(×10-3·m-1) | 曲率延性 | 屈服弯矩/ (kN·m) | 极限弯矩/ (kN·m) | |
| 1 | 墩顶 | 2.09 | 12.51 | 5.99 | 4 186 | 4 327 |
| 墩底 | 2.12 | 11.57 | 5.46 | 4 366 | 4 496 | |
| 2 | 墩顶 | 2.09 | 12.51 | 5.99 | 4 186 | 4 327 |
| 墩底 | 2.13 | 11.37 | 5.34 | 4 439 | 4 560 | |
根据算例桥梁尺寸及参数取值,采用SAP2000数值分析软件建立全桥有限元模型,其中上部梁体采用弹性梁单元模拟,桥墩采用可考虑塑性变形和滞回耗能的弹塑性梁单元模拟,对于板式橡胶支座,采用线弹性弹簧单元模拟,墩底固结,全桥有限元模型如图 3所示。桥梁的第1阶自振周期为0.92 s,顺桥向平动;第2阶自振周期为0.80 s,横桥向平动;第3阶自振周期为0.52 s,绕竖轴转动。算例桥梁的前3阶振型如图 4所示,从周期取值及各阶模态的分布可看出,符合典型公路RC连续梁桥的基本特征。
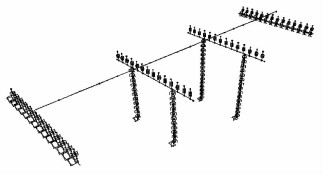 |
| 图 3 全桥有限元模型 Fig. 3 Finite element model of bridge |
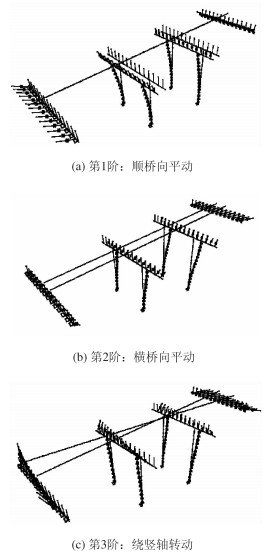 |
| 图 4 全桥模型的前3阶振型 Fig. 4 First 3 order vibration modes of bridge |
为了定量对比近、远场地震下桥梁动力响应及滞回耗能的差异,地震波的合理选取是重要基础。为了确保地震记录选取的代表性和科学性,本文地震记录选取按照以下原则:(1)所在地震事件的震级(M)大于6.5级;(2)加速度峰值PGA≥0.1g;(3)对于近场记录,其所在台站的断层投影距离df不大于15 km,且速度峰值PGV应大于50 cm/s,以确保具有较明显的速度脉冲存在;(4)对于远场记录,其断层距应df大于60 km。根据上述原则,分别选取了3条近场记录和3条远场记录,各条记录的基本参数分别如表 2所示。
| 记录名称 | 地震事件 | 震级M | 断层距df/km | 记录持时/s | PGA/(×g) | PGV/(cm·s) | PGV/PGA |
| B-PTS225 | Superstitn Hills(1987-11-24) | 6.7 | 0.70 | 22.35 | 0.455 | 112.0 | 246.2 |
| WPI046 | Northridge(1994-01-17) | 6.7 | 7.10 | 24.99 | 0.455 | 112.8 | 247.9 |
| WGK-N | Chi-Chi,Taiwan(1999-09-20) | 7.6 | 11.14 | 59.00 | 0.484 | 74.4 | 153.7 |
| NAS270 | Loma Prieta(1989-10-18) | 6.9 | 75.20 | 29.58 | 0.209 | 42.5 | 203.3 |
| CHY074 | Chi-Chi Taiwan(1999-09-20) | 7.6 | 82.49 | 90.00 | 0.234 | 28.1 | 120.1 |
| TCU083 | Chi-ChiTaiwan(1999-09-20) | 7.6 | 78.90 | 90.00 | 0.111 | 12.1 | 109.0 |
图 5(a)、(b)分别为近场记录和远场记录在5%阻尼比下的动力放大系数β谱及均值谱,对比可看出,近场地震均值谱在中、短周期段存在较宽的平台,而远场地震则在短周期段存在较高的峰值,但随周期的延长下降迅速,二者之间在频谱特性上存在较为明显的差别。
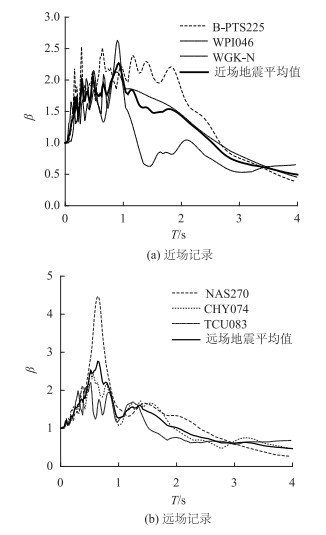 |
| 图 5 所选地震记录的动力放大系数β谱 Fig. 5 β spectra of dynamic magnification factor of selected ground motion records |
为了表述方便,定义墩高系数η[11]:

式中,h为桥墩某截面标高;H为桥墩总高度。则对于墩底η=0,对于墩顶η=1。对于1#桥墩和2#桥墩每柱分别设置的11个和15个弹塑性梁单元,第i个单元的损伤指标DIi采用改进的Park-Ang模型定义[8]:
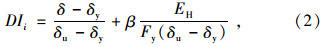
式中,δ为地震作用下构件实际变形;δy,δu分别为构件屈服位移和单调加载极限变形能力;β为累积耗能项权重系数,一般取0.15;Fy为屈服力;EHi为桥墩第i单元的滞回耗能。因此,可定义桥墩各单元损伤、滞回耗能参与系数γi和γEi为:
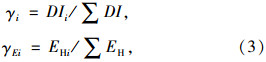
分别用于描述第i个弹塑性梁单元的损伤、累积滞回耗能占所在桥墩总损伤、总耗能的比值。下文中计算结果均依据桥墩双柱地震响应之和进行统计和分析。
3.2 地震动频谱特性、PGA和持时对滞回耗能和损伤分布特征的影响为了对比不同地震动强度水平、频谱特性等因素对滞回耗能EH及损伤DI沿桥墩高度分布特征的影响,将所选地震波的PGA分别调整为0.2g,0.3g,0.4g,0.5g和0.6g,通过非线性动力时程法对全桥模型进行求解,并自编Fortran程序进行能量积分及损伤计算(式(3)),以确定各墩不同部位的滞回耗能及地震动损伤。因2#桥墩高度更大,而全桥支座布置相同且跨度分布均匀,下文以2#墩为重点分析对象。图 6给出了不同PGA下6条记录的墩底单元滞回耗能时程曲线,可看出,随着PGA的增大,墩底的滞回耗能显著增大,且滞回耗能显著增加的时刻和地震记录PGA峰值出现的时刻相吻合,体现了地震动强度的作用。
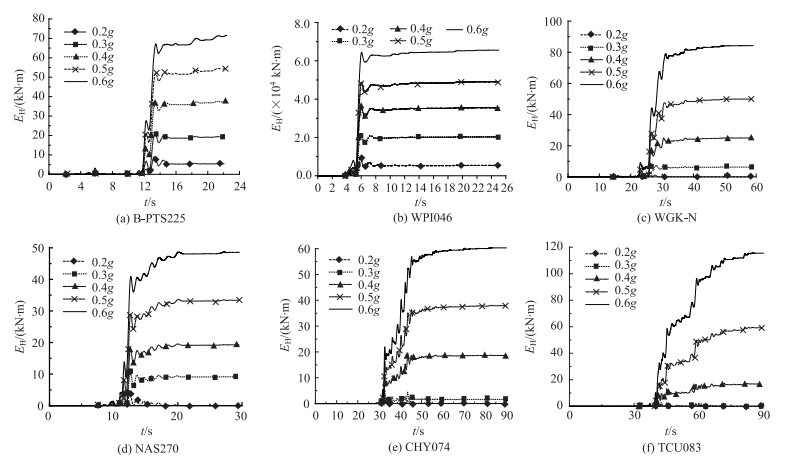 |
| 图 6 不同PGA下墩底单元滞回耗能时程曲线 Fig. 6 Time history curves of hysteretic energy of pier bottom element under different PGAs |
为了对比近、远场地震动频谱特性对桥梁结构地震响应的影响,将各条记录的PGA统一调整为0.4g,计算所得墩底单元滞回耗能时程曲线、滞回耗能EH及滞回耗能参与系数γEi在2#墩各部位的分布分别如图 7~图 8所示。从图 7可知,在相同的地震动强度(PGA)下,不同地震波下墩底滞回耗能时程存在明显差别,3条近场地震波B-PTS225、WPI046和WGK-N的PGV/PGA值分别为246.2,247.9,153.7,不同记录下的墩底滞回耗能大体与上述比值呈正比例关系;对于3条远场地震波NAS270、CHY074和TCU083,其PGV/PGA值分别为203.3,120.1,109.0,墩底滞回耗能也存在类似关系。这说明地震动频谱特性对滞回耗能的影响显著,通过PGV/PGA指标可得到直观的体现,即PGV/PGA增大会导致滞回能量指标的明显增加。从近、远场地震下的对比也可看出,近场地震下总体具有更高的PGV/PGA值,因此其滞回耗能量值也明显高于远场。
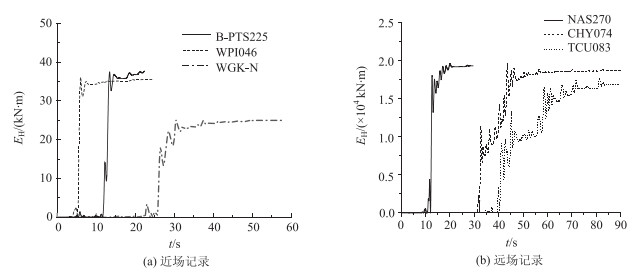 |
| 图 7 不同记录下墩底单元滞回耗能时程曲线 Fig. 7 Time history curves of hysteretic energy of pier bottom element in different records |
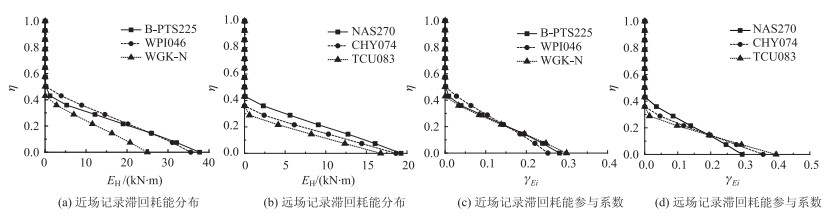 |
| 图 8 不同记录下滞回耗能及其参与系数分布 Fig. 8 Distributions of hysteretic energy and its participation factors in different records |
图 8给出了滞回耗能及滞回耗能参与系数γEi在2#墩各部位的分布,可看出,不同地震记录下滞回耗能分布均呈现下大上小的规律,由墩底向上快速减小,所占比例随墩高逐渐降低。此外,从图 8(a)、(b)可看出,地震波频谱特性对沿墩高不同部位滞回耗能的量值影响明显,随地震记录PGV/PGA的增大,桥墩不同部位滞回耗能也随之增大。图 9给出了近、远场地震下结构损伤、损伤参与系数γi两个指标沿墩高的分布,和滞回耗能的分布类似,不同部位的损伤程度也受到地震动频谱的影响见图 9(a)、(b),PGV/PGA越大,墩底损伤显著增加,但损伤参与系数γi的分布基本一致,见 图 9(c)、(d)。
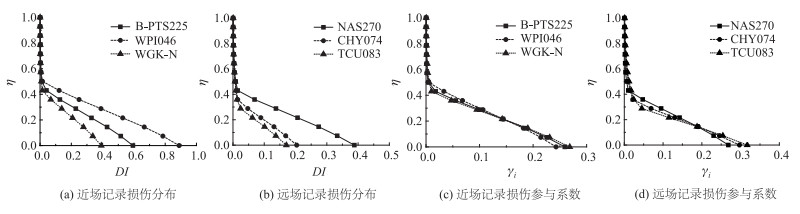 |
| 图 9 不同记录下损伤及其参与系数分布 Fig. 9 Distributions of damage and its participation factors in different records |
加速度峰值(PGA)是地震动三要素之一,为了定量对比不同PGA水平的近、远场地震下桥梁结构能量及损伤的量值和分布特性,将近、远场地震下各项指标取均值进行对比讨论。图 10(a)、(b)给出了不同PGA下滞回耗能沿墩高的分布,可看出,两种类型的地震下,滞回耗能均呈现下大上小的特征,在墩底以上不同高度(η≤0.5)范围内发生塑性变形耗能,且随着PGA的增大,各部位滞回耗能随之增大。存在的差异在于,近场地震下各部位的滞回耗能明显大于远场地震,如PGA=0.2g时,近场地震下墩底滞回耗能均值为3.6 kN·m,而远场地震下为0,表明尚处于弹性状态,这也是图 10(d)和图 11(d)中没有给出PGA=0.2g时的滞回耗能参与系数γEi及损伤参与系数的原因;PGA=0.4g 时,近场地震下墩底滞回耗能均值为32.7 kN·m,远场地震下为18.2 kN·m,差距明显。图 10(c)、(d)为不同PGA下滞回耗能参与系数γEi的分布,可以看出,两类地震下参与系数的分布特征类似,当PGA较小时滞回耗能主要集中在墩底,近、远场下γEi的最大值分别为0.38和0.4;随着PGA的增大γEi沿墩高分布更加均匀,PGA=0.6g时墩底处γEi分别降低为0.25和0.28。对比可发现,在墩底附近一定范围内(约η≤0.15),近场地震下桥墩各部位的滞回耗能参与系数小于远场地震,而在该截面以上则大于远场,体现了两类地震作用下能量分布的差异。
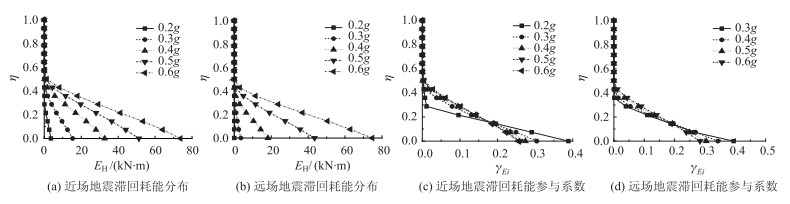 |
| 图 10 不同PGA下滞回耗能及其参与系数分布 Fig. 10 Distributions of hysteretic energy and its participation factors under different PGAs |
图 11(a)、(b)为不同PGA下损伤沿墩高的分布,可看出,和滞回耗能指标类似,损伤的分布也沿墩高下大而上小,且随着PGA的增大桥墩各部位的损伤水平随之增大。对比可发现,近场地震下各部位的损伤明显大于远场地震,如PGA=0.6g时,近场下墩底损伤指标DI超过1.1(达到“倒塌”状态[11]),而在远场下则不到0.7(“严重损伤”状态)。图 11(c)、(d)为不同PGA下损伤参与系数的分布,可看出,随PGA增大,γi在墩底处有所降低,但随高度增加而有所增大,两类地震下规律类似,在γi的具体取值上也大体相同。
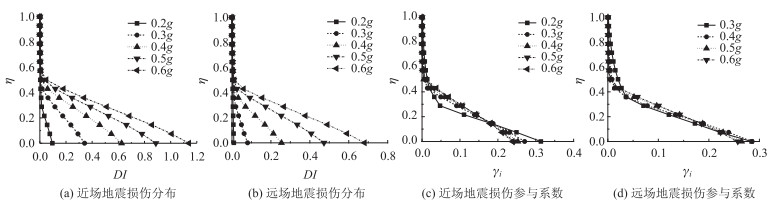 |
| 图 11 不同PGA下损伤及其参与系数分布 Fig. 11 Distributions of damage and its participation factors under different PGAs |
为了进一步对比两类地震作用下的差异,图 12、图 13给出了PGA为0.4g和0.6g时各项指标的对比图。图 12(a)和12(b)分别为PGA=0.4g,0.6g时滞回耗能沿墩高分布的对比,可明显看出,当PGA=0.4g时,近场地震下桥墩各部位的滞回耗能明显大于远场地震,如近、远场下墩底滞回耗能分别为32 743 kN·m和18 223 kN·m;而在PGA=0.6g时,二者之间差别趋小,在墩底处近场下稍大,随墩高的增加差别趋于明显。
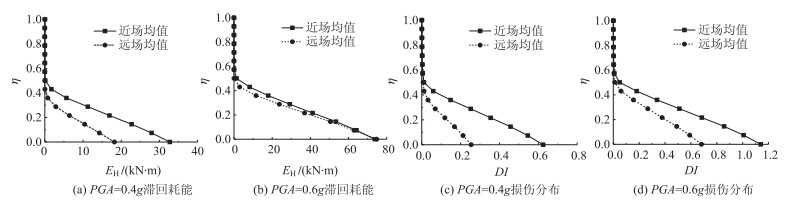 |
| 图 12 近、远场滞回耗能及损伤分布 Fig. 12 Distributions of hysteretic energy and damage in near-field and far-field |
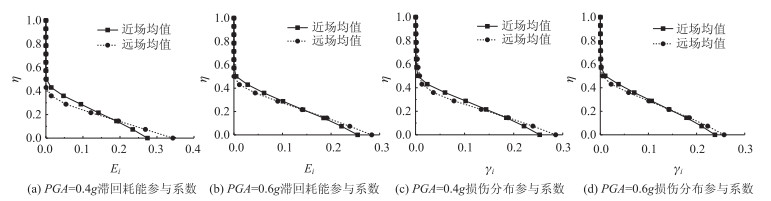 |
| 图 13 近、远场滞回耗能参与系数及损伤参与系数分布 Fig. 13 Distributions of hysteretic energy and its participation factors in near-field and far-field |
图 12(c)和12(d)分别为PGA=0.4g,0.6g时损伤沿墩高分布的对比,和图 12(a)、(b)所示的能量指标类似,当PGA=0.4g时,近场地震下桥墩各部位的损伤明显大于远场地震,如对于墩底,近场地震下DI为0.63(“严重损伤”状态),远场地震下为0.25(“中等损伤”状态),此外近场地震下桥墩损伤出现的高度(η=0.501)也比远场(η=0.430)大。当PGA=0.6g时,近场地震下桥墩各部位的损伤仍明显大于远场地震,仍以墩底为例,近场地震下DI为1.14(“完全倒塌”状态),远场地震下DI为0.68 (“严重损伤”状态),同样地,近场地震下桥墩损伤出现的高度(η=0.573)也比远场(η=0.501)大。这一现象和PGA=0.6g时能量的分布特征存在一定差异(图 12(b)),这是由于总体损伤是由能量和变形两方面共同决定的,虽然此时能量的差异不是太大,但近场强震更大的变形需求导致了更高的总体损伤。
图 13为两种PGA水平下滞回耗能参与系数γEi及损伤参与系数γi沿墩高分布的对比,总体来看,两类地震下滞回耗能参与系数及损伤参与系数的差异并不突出,这和图 12中能量和损伤的分布差异有明显区别。但仍可看出,在墩底以上一定范围内,近场地震下滞回耗能和损伤的参与比例小于远场,而在该范围以外则大于远场。
和图 10、图 11中类似,这种现象的出现,是源于两种地震动类型在频谱特性上的差异,导致近场地震下损伤与耗能沿桥墩向上扩展,各部位对应的滞回耗能和损伤也随之增大,因此靠近墩底处的滞回耗能和损伤所占比例相应减小。因此,同等条件下近场地震对桥梁造成的危害更加突出。
3.2.3 近、远场不同持时的影响对比在结构的非线性阶段,地震导致的结构损伤有可能存在时间上的累积效应。为了对比讨论强震持时对于结构损伤及滞回耗能的影响,将所选近、远场各3条记录的PGA统一调整为0.4g,并通过对地震记录进行持时修正,将其有效持时td分别调整为0.5,1.0和2.0倍的95%强震持时[20],以分别构造具有不同持时的记录组合。
图 14(a)、(b)为不同持时水平的近、远场地震下2#墩损伤的分布,总体来看,两种地震动类型下,桥墩各部位损伤均随有效持时td的增加而增大,以墩底为例,3种持时水平下,近场地震下墩底损伤DI值分别为0.42,0.62和0.84,增长显著;远场地震下分别为0.24,0.26和0.33,也存在较明显增长。对比可看出,在同样的持时水平下,近场地震下的损伤高于远场,且损伤随持时增加的增长幅度也明显高于远场,这是由于近场地震对结构有更高的非弹性变形需求,因而所产生的累积效应更加明显,否则在低强度的地震动作用下,持时难以引起损伤的显著累加,如图 14(b)中所示,在由0.5td增加到1.0td时,各部位损伤增加并不显著。
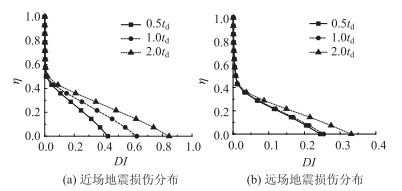 |
| 图 14 不同持时下损伤分布 Fig. 14 Distributions of damage in different durations |
图 15和图 16分别给出了不同持时水平下滞回耗能参与系数γEi及损伤参与系数γi的对比,可看出,随有效持时的增加,两类地震下墩底处的滞回耗能和损伤所占比例有所下降,而随高度增加有所增长,但变化的幅度并不明显。和图 13所揭示的规律类似,在靠近墩底的一定范围内,不同持时水平下近场地震的滞回耗能和损伤参与比例小于远场。而在该区域以上,近场地震下滞回耗能和损伤的参与比例则大于远场,表明近场地震下桥墩的滞回耗能和损伤分布更加均匀,例如,在墩底处,对于滞回耗能,近、远场下的γEi分别约为0.27和0.34;对于损伤,近、远场下的γi分别约为0.25和0.29,存在较明显的差异。
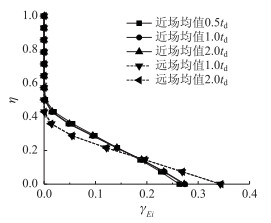 |
| 图 15 不同持时下滞回耗能参与系数分布 Fig. 15 Distributions of hysteretic energy participation factors in different durations |
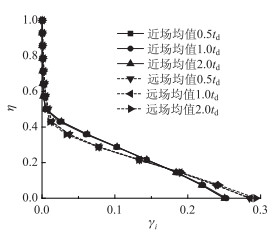 |
| 图 16 不同持时下损伤参与系数分布 Fig. 16 Distributions of damage participation factors in different durations |
本文以双柱式桥墩RC连续梁桥为对象,从地震动频谱、峰值加速度和持时等特性参数的角度,对比讨论了近、远场两类地震下滞回耗能、损伤在量值及其分布上的差异特征,可得到以下结论:
(1)两类地震下,滞回耗能及损伤沿墩高自下而上急剧减小,随着PGA增大,桥墩各部位的滞回耗能及损伤明显增大,损伤出现的高度也有所扩大。
(2)滞回耗能及损伤参与系数沿墩高的分布大体稳定,随着PGA的增大,靠近墩底的一定范围内损伤及滞回耗能所占比例有所下降,而在此范围以外,各部位损伤及滞回耗能参与程度逐渐增加。
(3)地震动频谱特性对于桥梁地震响应有显著影响,PGV/PGA增大,会导致桥墩滞回耗能和损伤指标的显著增加。随有效持时增长,强震下桥墩各部位的滞回耗能及损伤相应增大,但持时对滞回耗能及损伤参与系数分布的影响不明显。
(4)在相同的PGA和持时水平下,近场地震下桥墩各部位的滞回耗能及损伤程度均明显大于远场,且损伤沿桥墩出现的高度也更大。
(5)在靠近墩底的一定范围内,近场地震下的滞回耗能和损伤所占比例小于远场,而在该区域以上则大于远场,表明近场地震下桥墩的滞回耗能和损伤分布更加均匀。对比可发现,近场地震对桥梁结构提出了更高的耗能和变形需求,且向桥墩上部延伸更加明显,对桥梁抗震设计提出了更高的要求。
需说明的是,本文研究结论适用于中等高度桥墩的RC桥梁,因所选记录有限,还有待在后续研究中进一步加强和补充,并对比讨论考虑支座非线性之后的响应特性。
| [1] | Applied Technology Council. Seismic Evaluation and Retrofit of Concrete Building,ATC-40[R]. Redwood City:Applied Technology Council,1996. |
| [2] | Federal Emergency Management Agency (FEMA). Recommended Seismic Design Criteria for New Steel Moment Frame Buildings,FEMA-350[R]. Washington,D.C.:Federal Emergency Management Agency,2000. |
| [3] | Federal Emergency Management Agency (FEMA). Pre-standard and Commentary for the Seismic Rehabilitation of Buildings,FEMA-356[R]. Washington,D.C.:Federal Emergency Management Agency,2000. |
| [4] | CECS160:2004,建筑工程抗震性态设计通则(试用)[S]. CECS160:2004,General Rule for Performance- based Seismic Design of Buildings (on Trial)[S]. |
| [5] | 马宏旺,吕西林.建筑结构基于性能抗震设计的几个问题[J].同济大学学报:自然科学版,2002,30(12):1429-1434. MA Hong-wang,LV Xi-lin. Some Problems about Performance-based Seismic Design[J]. Journal of Tongji University:Natural Science Edition,2002,30(12):1429-1434. |
| [6] | BERTERO R D,BERTERO V V. Performance-based Seismic Engineering: The Need for a Reliable Conceptual Comprehensive Approach[J]. |
| [7] | MOEHLE J,DEIERLEIN G G. A Framework Methodology for Performance-based Earthquake Engineering[C]//Proceedings of 13th World Conference on Earthquake Engineering. Vancouver,Canada:Canadian Association for Earthquake Engineering,2004:3812-3824. |
| [8] | 江辉,朱晞.以性能指标为控制变量的强度折减因子[J].铁道学报,2008,26(6):88-95. JIANG Hui, ZHU Xi. Strength Reduction Factor Model with Performance Index as Control Parameter[J]. Journal of the China Railway Society, 2008,26(6):88-95. |
| [9] | 朱晞,江辉.基于性能指标的桥梁墩柱抗震设计方法[J]. 土木工程学报,2009,42(4):85-92. ZHU Xi,JIANG Hui. Performance-based Seismic Design Method for RC Bridge Piers[J]. China Civil Engineering Journal,2009,42(4):85-92. |
| [10] | 王丰,李宏男,伊廷华.钢筋混凝土结构直接基于损伤性能目标的抗震设计方法[J]. 振动与冲击,2009,28(2):128-131. WANG Feng,LI Hong-nan,YI Ting-hua. Direct Damage-based Seismic Design Methodology for RC Structure[J]. Journal of Vibration and Shock,2009,28(2):128-131. |
| [11] | 江辉,慎丹,刘夏润,等. 基于改进Park-Ang模型的RC桥墩地震动损伤及滞回耗能特性研究[J].振动与冲击,2012,31 (5):97-105. JIANG Hui,SHEN Dan,LIU Xia-Run,et al. Seismic Damage and Hysteretic Energy Dissipation Characteristics of a RC Bridge Pier Based on Improved Park-ang Model[J]. Journal of Vibration and Shock,2012,31 (5):97-105. |
| [12] | SOMERVILLE P G. Characterizing Near Fault Ground Motion for the Design and Evaluation of Bridges[C]//Proceedings of the 3th National Conference and Workshop on Bridges and Highways. New York:State University of New York at Buffalo:137-148. |
| [13] | 王海云,谢礼立.近断层强地震动的特点[J].哈尔滨工业大学学报,2006,38(12):2070-2072. WANG Hai-yun,XIE Li-li. Characteristics of Near-fault Strong Ground Motions[J]. Journal of Harbin Institute of Technology,2006,38(12):2070-2072. |
| [14] | 李爽,谢礼立.近场问题的研究现状与发展方向[J].地震学报,2007,29(1):102-111. LI Shuang,XIE Li-li. Progress and Trend on Near-field Problems in Civil Engineering[J]. Acta Seimologica Sinica,2007,29(1):102-111. |
| [15] | JONSSON M H,BESSASON B,HAFLIDASON E. Earthquake Response of a Based-isolated Bridge Subjected to Strong Near-fault Ground Motion[J]. |
| [16] | 王东升,孙治国,郭迅,等.汶川地震桥梁震害经验及抗震研究若干新进展[J]. 公路交通科技,2011,28(10):44-53. WANG Dong-sheng,SUN Zhi-guo,GUO Xun,et al. Lessons Learned from Wenchuan Seismic Damages and Recent Research on Seismic Design of Highway Bridges[J]. Journal of Highway and Transportation Research and Development,2011,28(10):44-53. |
| [17] | BROWN A,SAⅡDI M S. Investigation of Effect of Near-fault Motions on Substandard Bridge Structures[J]. |
| [18] | 慎丹.近场地震作用下RC梁式桥抗震设计几个关键问题的研究[D].北京:北京交通大学,2011. SHEN Dan. Research of Several Key Problems on Seismic Design of RC Girder Bridges under Near-field Earthquake[D]. Beijing: Beijing Jiaotong University,2011. |
| [19] | JTG/T B02—01—2008,公路桥梁抗震设计细则[S] . JTG/T B02—01—2008,Guidelines for Seismic Design of Highway Bridges[S]. |
| [20] | TRIFUNAC M D,BRADY A G. A Study on the Duration of Strong Earthquake Ground Motion[J]. Bulletin of Seismological Society of America,1975,5(3):581-626. |
 2015, Vol. 32
2015, Vol. 32
