扩展功能
文章信息
- 黄石, 袁万城
- HUANG Shi, YUAN Wan-cheng
- 年温差对采用拉索减震支座斜拉桥抗震性能影响分析
- Analysis of Effect of Annual Temperature Difference on Seismic Performance of Cable-stayed Bridge with Cable-sliding Friction Aseismic Bearings
- 公路交通科技, 2015, Vol. 32 (9): 57-63,73
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 32 (9): 57-63,73
- 10.3969/j.issn.1002-0268.2015.09.010
-
文章历史
- 收稿日期: 2014-11-26
近年来我国先后建成了多座大跨径斜拉桥,鉴于我国地震的多发性,研究斜拉桥体系在地震作用下的响应特征是一项关键课题。斜拉桥按力学性能可以分为漂浮体系、竖向支撑体系、塔梁墩固结体系等形式。对于斜拉桥抗震而言,常采用的方案是在主梁和桥塔之间设置支座及相应的减隔震装置,在减小梁端位移的同时将可能降低主塔地震力。国内外建成的大跨度斜拉桥中有不少采用减隔震装置的实际应用,包括在塔梁之间设置大型橡胶隔震支座、纵向钢绞线拉索或阻尼器装置等措施[1, 2, 3]。上述措施中,橡胶隔震装置自回复能力差,地震过后不能有效复位;钢绞线拉索能够有效地限制梁、墩相对位移,但梁体局部构造复杂,需要特别设计;阻尼器装置主要依靠本身的塑性变形消耗地震能量,但当塑性变形进入屈服阶段后,阻尼器的耗能能力大大降低,且阻尼器价格昂贵也不利于其推广使用[4]。
斜拉桥合龙段施工时,一般会选择在一个较理想的温度下进行,称为设计基准温度。从年温差的角度来看,夏季最高温度以及冬季最低温度均与基准温度相差较大。对于已经合龙完成的塔梁固结体系斜拉桥而言,因其梁体长度很大,年温差引起不可忽略的梁体变形,并导致滑动支座产生较大位移量[5, 6]。对于塔梁固结、墩梁之间设置支座的斜拉桥,较大的支座位移会对整座桥的地震响应产生影响。目前国内外对于考虑年温差作用的斜拉桥抗震性能研究基本还是空白,而我国的桥梁规范亦欠缺对于温度与地震作用耦合效应的相关规定[7, 8, 9]。
本文旨在将拉索减震支座应用于斜拉桥体系中,并以一座采用拉索减震支座的六塔七跨斜拉桥为工程背景,建立sap2000有限元模型并在顺桥向输入地震动,采用非线性时程分析方法计算不同温度条件下全桥模型的地震响应,进而研究拉索减震支座对于控制墩梁固结体系斜拉桥墩梁位移的有效性,并讨论年温差对采用拉索减震支座的塔梁固结体系斜拉桥抗震性能的影响。本文研究温度对支座的影响并非指因温度变化而引起支座材料力学性能的变化[10],而是指拉索减震支座在梁体产生温度变形时出现初始剪切变形。
1 拉索减震支座简介 1.1 支座构造特点及工作原理拉索减震支座(CSFAB)是由同济大学袁万城教授研制开发的新型减隔震支座,是在普通盆式支座的基础上结合国内普遍采用的限位弹性索装置而成。该支座创造性的将盆式支座(或球型钢支座)的摩擦耗能特性与拉索装置的限位功能结合起来,其中拉索具有易更换性,便于日常维护以及震后修复。拉索减震支座能够传递上部结构的荷载,并能满足由于温度变化、汽车制动、混凝土梁体收缩等所引起梁体位移和转动要求。在正常使用情况下,拉索减震支座中的拉索不发挥作用,支座与普通盆式橡胶支座的性能相同。而在强震作用下,拉索能够发挥限制主梁与下部结构相对位移的作用,从而有效避免落梁、梁体碰撞等震害发生[11, 12]。
根据工程需要,拉索减震支座可分为固定型和滑动型支座。其中固定支座通过在支座中间设置抗剪螺栓限制支座水平位移,而取消固定支座中的抗剪螺栓即为滑动支座。在正常使用状态及中小地震下,抗剪螺栓能够保证支座是固定的,此时水平荷载由固定支座传递给固定墩[13];在强震、船撞等极端状态下,支座水平荷载超过设计值时,抗剪螺栓剪断,固定支座转变为滑动支座,结构体系的传力特性发生改变,同时水平荷载分摊给各个桥墩[13]。图 1和图 2分别为拉索减震支座的构造示意图和实物图。
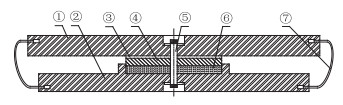 |
| ①上支座板;②下支座板;③不锈钢板;④中间钢板(上表面涂四氟乙烯);⑤抗剪螺检;⑥橡胶支承层;⑦易更换式拉索 图 1 固定型拉索减震支座构造 Fig. 1 Configuration of fixed CSFAB |
 |
| 图 2 拉索减震支座实物图 Fig. 2 A photograph of CSFAB |
拉索减震支座是在普通盆式橡胶支座的基础上设置限位拉索而成,因此其恢复力模型可视为由盆式支座和拉索二者的恢复力模型叠加而成。如图 3(c)所示为拉索减震支座的恢复力模型。
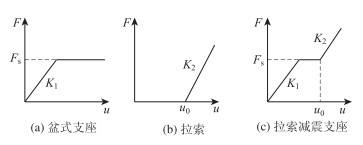 |
| 图 3 拉索减震支座恢复力模型 Fig. 3 Restoring force model of CSFAB |
其中,图 3(a)中盆式橡胶支座的恢复力模型类似理想弹塑性材料的应力-应变关系。K1为滑动盆式支座的弹性刚度,Fs为临界摩擦力,可按下式计算:

式中,μ为滑动摩擦系数;N为支座的竖向压力。
图 3(b)中,拉索的恢复力模型为线性。拉索开始发挥限位作用时的位移u0称为拉索减震支座的自由程,K2为拉索的水平约束刚度,可按式(2)计算:

式中,E为拉索(钢绞线)的弹性模量;A为拉索截面总面积;L为拉索索长。
拉索减震支座应满足如下特征:
(1)当支座位移不超过自由程位移u0时,拉索不发挥限位功能,此阶段拉索减震支座恢复力模型与盆式橡胶支座恢复力模型一致;
(2)当支座位移超过自由程位移后,拉索开始提供水平方向额外约束,支座的刚度发生突变。此时恢复力曲线的斜率即为拉索的水平约束刚度K2。由于K2远大于K1,此阶段支座发生单位位移所需力迅速增大,这是拉索发挥限位作用的力学机理。
2 工程背景与桥梁有限元模型的建立 2.1 工程背景本文所依据的工程背景为一座六塔七跨斜拉桥,跨径布置为(79+5×150+79)m=908 m。该斜拉桥的结构体系采用塔梁固结,梁墩之间设置支座的形式,塔柱采用分叉形式与主梁结合[14]。该六塔七跨斜拉桥的结构示意图如图 4所示,其中,2#~7#为主墩,1#和8#为主桥与引桥之间的过渡墩。
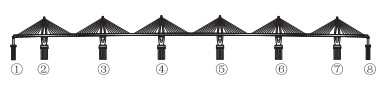 |
| 图 4 六塔七跨斜拉桥结构示意图 Fig. 4 Structural representation of 6-pylon 7-span cable-stayed bridge |
斜拉桥主塔为钢筋混凝土人形塔,主梁为组合箱梁形式,即主梁顶板和底板采用预应力混凝土结构,腹板采用波形钢腹板。主梁截面示意图见图 5。主墩基础采用钻孔灌注桩群桩基础,桩数18根,桩径2.2 m。
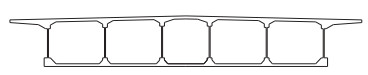 |
| 图 5 主梁截面 Fig. 5 Cross-section of main girder |
斜拉桥支座布置形式如图 6所示,每个主墩均在中间布置4个大吨位支座,在横桥向两侧布置4个小吨位支座,两个过渡墩上各设2个小吨位支座。其中,固定支座设置在4#墩(称为固定墩)上。
 |
| 图 6 斜拉桥支座布置形式示意图 Fig. 6 Arrangement of bearings of cable-stayed bridge |
本文采用SAP2000通用有限元分析软件建立该六塔七跨斜拉桥的有限元分析模型。其中,桥塔、主梁以及桥墩采用框架单元模拟,斜拉索采用释放两端弯矩的框架单元模拟,其拉伸刚度采用考虑垂度效应的等效拉伸刚度。塔单元与主梁单元在结合处采用两节点body形式固结起来以模拟塔梁结合。在主梁两侧建立与主梁单元相固结的两节点,作为主梁同斜拉索的连接节点。组合梁的截面特性由spc截面特性计算器计算得到。
本文为考虑六塔七跨斜拉桥的桩基边界条件,将承台简化为节点并附以承台质量,在承台节点底用6个自由度的弹簧刚度模拟桩土作用,弹簧刚度值根据土质资料由pile软件计算确定。同时,为了考虑斜拉桥相邻结构的影响,取主桥左右的引桥作为边界条件。
根据前文所述,拉索减震支座可视为盆式支座和弹性拉索组合而成,该支座的模拟也可采用两者模拟组合而成。在sap2000软件中,盆式支座采用Plastic(Wen)连接单元模拟,弹性拉索采用多线段弹性连接单元(Multi-linear Elastic)模拟,这两种连接单元的本构关系分别如图 7和图 8所示。
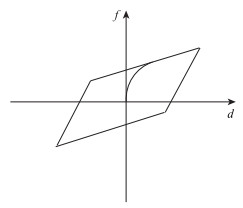 |
| 图 7 塑性Wen单元力与位移关系曲线 Fig. 7 Force-displacement curve of plastic Wen element |
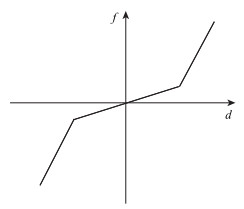 |
| 图 8 多线段弹性连接单元力与位移关系曲线 Fig. 8 Force-displacement curve of multi-segment elastic linkage element |
将这两种连接单元的属性同时指定到需要设置支座的两点之间,即可模拟拉索减震支座的本构关系。通过改变Multi-linear Elastic连接单元的相关参数可以设置拉索减震支座的自由程、刚度等属性。由年温差引起的支座初始剪切位移主要影响拉索的自由程,因此在多线段弹性连接单元的定义中,可以通过调整图 8中曲线与位移轴的交点位置模拟初始剪切变形的大小。
全桥的有限元分析模型如图 9所示。
 |
| 图 9 六塔七跨斜拉桥有限元分析模型 Fig. 9 FEA model 6-pylon 7-span cable-stayed bridge |
滑动支座位移量是指桥梁施工阶段结束后,滑动支座的上支座板偏移支座理论中心线的位移量,亦称为支座剪切变形量。滑动支座位移量主要分为两个部分:由于体系温差导致梁体变形所引起的位移量Δ1和由于梁体弹性压缩及混凝土收缩徐变引起的位移量Δ2[12]。由于文章篇幅所限,本文仅讨论年温差作用对斜拉桥滑动支座的影响。
为考虑温差效应对斜拉桥滑动支座位移量的影响,首先需要确定结构中的温度不动点。温度不动点的定义为:在桥跨结构的形心面上存在一点,当桥跨结构上所有质点由温度变化而产生应变时,该点保持不动,则此点为不动点。由于多塔斜拉桥的施工工艺复杂,周期较长,确定施工过程中的温度不动点非常困难,也无必要。为简化考虑,本文假设多塔斜拉桥在设计基准温度下完成施工,此时固定墩上设置固定支座,其他墩上的滑动支座无初始温度位移量。在成桥之后,当温度变化引起斜拉桥主梁伸缩时,固定支座因设置抗剪螺栓保持位置不变,而滑动支座则会产生靠近或远离固定墩的位移量。因此,可以将斜拉桥的固定墩确定为温度不动点。滑动支座的位移量可以根据公式Δl=αlΔT近似计算得出,式中,α为斜拉桥主梁的线膨胀系数,本文中可取为0.00 001;l为滑动支座到温度不动点的梁体长度;ΔT为结构实际温度与设计基准温度之差。
3.2 年温差效应的考虑根据《公路桥涵设计通用规范》的规定,计算桥梁结构因均匀温度作用引起的外加变形或约束变形时,应从受到约束的结构温度开始,考虑最高和最低有效温度的作用效应。斜拉桥合龙可以视为结构受到约束的开始。
本文结合规范以及该斜拉桥桥址处的具体气温情况,分别取最高有效温度(T1)和最低有效温度(T2)为34 ℃和-6 ℃,取主桥的结构合龙温度T0为14 ℃,即合龙温度与最高、最低温度相差均为20 ℃。本文以桥梁结构在发生地震时的实际温度(简称震时温度)为改变参数,参数的取值范围的上下限分别为最高和最低温度。
为研究温度变化对桥梁结构抗震性能的影响,同时对拉索减震支座的限位特性进行验证,分别设置如下3类工况:
工况1,取结构震时温度T=14 ℃,全桥的支座均采用普通盆式支座,4支座为固定支座;
工况2,取结构震时温度T=14 ℃,2#和7#支座采用滑动拉索减震支座,其余支座为普通盆式支座,4#支座为固定盆式支座;
工况3~6,考虑温度变化,分别取结构震时温度T为-6,4,24,34 ℃,2#和7#支座采用滑动拉索减震支座,其余支座为普通盆式支座,4#支座为固定盆式支座。
针对3类工况条件分别建立桥梁有限元模型,并对各有限元模型的地震响应进行比较分析。
在有限元模型中,限位拉索刚度K2取为5×105 kN/m,自由程位移u0取0.15 m。在定义Multi-linear Elastic连接单元时,通过调整多线性力-变形定义中的位移量来考虑不同温差引起的支座初始位移量。对于不同温度条件,2#墩和7#墩处拉索支座(称为2#支座和7#支座)会发生不同初始剪切变形,变形量可以根据前文公式Δl=αlΔT计算得出。例如在34℃条件下,2#墩的拉索减震支座发生远离固定墩的初始变形量Δl=0.00 001×300 mm×20=0.06 m,可以在定义Multi-linear Elastic连接单元的力-位移关系时,将本构曲线与位移轴的交点设在0.06 m处。
4 桥梁有限元模型的地震响应分析 4.1 桥梁有限元模型的地震动输入本文采用sap2000有限元软件对全桥模型进行非线性时程分析。根据《城市桥梁抗震设计规范》规定,本文中六塔七跨斜拉桥的抗震设防分类为甲类。按照该斜拉桥的地震安评报告的结论,本文选取E2地震作用下(50 a超越概率为2%)的3条地震时程波作为有限元模型的地震动输入。图 10是所选取的3条地震时程波。
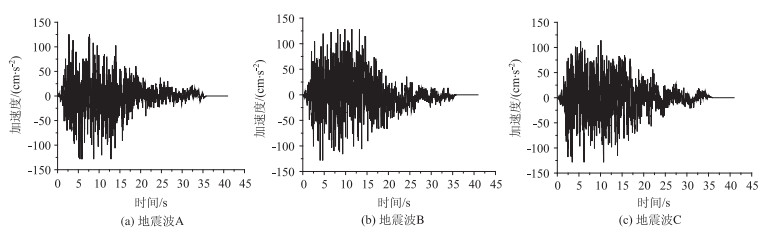 |
| 图 10 所选择的地震时程波 Fig. 10 Selected earthquake time-history waves |
由于年温差作用在纵桥向的影响远大于横桥向,本文中对桥梁有限元模型进行时程分析时仅考虑纵桥向的地震输入[15]。
4.2 拉索减震支座限位有效性分析为了验证拉索减震支座对于控制塔梁固结体系斜拉桥中墩梁相对位移的有效性,本节提取在3条地震波输入情况下,工况1和工况2中各主墩顶部出现的最大墩梁相对位移值并列入表中,如表 1所示。
| 地震波 | 工况类别 | 2# | 3# | 4# | 5# | 6# | 7# |
| A | 工况1/cm | 28.48 | 28.49 | 28.51 | 28.53 | 28.58 | 28.59 |
| 工况2/cm | 17.51 | 17.52 | 17.55 | 17.55 | 17.57 | 17.58 | |
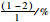 | 38.52 | 38.50 | 38.44 | 38.49 | 38.52 | 38.51 | |
| B | 工况1/cm | 29.38 | 29.41 | 29.42 | 29.42 | 29.42 | 29.44 |
| 工况2/cm | 18.12 | 18.12 | 18.13 | 18.13 | 18.13 | 18.14 | |
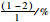 | 38.33 | 38.39 | 38.38 | 38.38 | 38.38 | 38.38 | |
| C | 工况1/cm | 27.96 | 27.97 | 27.97 | 28.01 | 28.04 | 28.05 |
| 工况2/cm | 17.33 | 17.35 | 17.36 | 17.35 | 17.37 | 17.37 | |
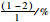 | 38.02 | 37.97 | 37.93 | 38.06 | 38.05 | 38.07 |
从表 1中数据可以看出,在3条地震波输入情况下,两种工况均有明显的墩梁相对位移。这是由于在本文中所选取的地震波输入情况下,两种工况中固定支座抗剪螺栓因承受的水平地震作用超过其抗剪能力而发生剪切破坏。此时,固定支座转换为滑动支座,全桥的结构体系发生转变,各墩的支座协同抗震,分摊水平地震作用力,能够避免出现地震水平力主要由固定墩承担的不利情况。但与此同时,会造成梁体纵桥向约束显著降低,从而导致墩梁之间出现较大的相对位移。
通过比较可以得出,工况2下墩梁的最大相对位移较之工况1显著减小,减小幅度达38%左右。这是因为在工况1中,抗剪螺栓剪切破坏之后,纵桥向的约束降低,墩梁相对位移所受限制不足;而在工况2中,当墩梁相对位移超过自由程位移之后,2#和7#拉索减震支座能够提供额外的梁体纵向约束刚度,使得工况2中梁体纵向约束较之工况1有显著提高,从而能有效地控制墩梁相对位移。
与全漂浮体系斜拉桥中由斜拉索将主梁地震力传递给桥塔的受力方式不同,塔梁固结体系斜拉桥通过在梁墩之间设置支撑装置,使主梁地震力经由支座传递给桥墩。本文在关注墩梁之间相对位移的同时,还对各墩墩底剪力值做相应分析,提取工况1和工况2中各墩最大墩底剪力值,如表 2所示。
| 地震波 | 工况类别 | 2# | 3# | 4# | 5# | 6# | 7# |
| A | 工况1/kN | 27 659 | 27 619 | 27 296 | 27 507 | 27 380 | 28 008 |
| 工况2/kN | 36 016 | 24 520 | 25 570 | 22 903 | 22 416 | 35 293 | |
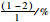 | -30.21 | 11.22 | 6.32 | 16.74 | 18.13 | -26.01 | |
| B | 工况1/kN | 28 533 | 28 492 | 28 159 | 28 376 | 28 245 | 28 893 |
| 工况2/kN | 37 360 | 25 263 | 26 346 | 23 658 | 23 156 | 36 202 | |
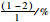 | -30.94 | 11.33 | 6.44 | 16.63 | 18.02 | -25.30 | |
| C | 工况1/kN | 27 154 | 27 115 | 26 798 | 27 005 | 26 880 | 27 497 |
| 工况2/kN | 35 154 | 24 090 | 25 121 | 21 466 | 21 988 | 34 652 | |
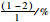 | -29.46 | 11.16 | 6.26 | 20.51 | 18.20 | -26.02 |
从表 2中可以看出,工况1情况下,斜拉桥各墩受力更加均衡,即在地震力作用下,所有墩共同抵抗地震作用的影响。在工况2中,设置拉索减震支座的2#墩和7#墩的墩底剪力较其他墩更大,且大于工况1中相应墩的墩底剪力。由此可见,桥墩设置拉索减震支座,在降低墩梁相对位移的同时会增大墩底所受地震剪力,但地震剪力的增幅为30%左右,各墩承担的地震作用基本能保持较合理的分配。由于在实际桥梁设计中,各墩的抗震能力设计趋近一致,工况2中拉索减震支座的布置方式能够发挥各墩抵抗地震作用的能力。在工程应用时,通过合理调整拉索刚度和自由程等各项参数,可以使得拉索减震支座在降低墩梁相对位移和增大墩底剪力两方面之间达到平衡点,既能减小桥墩的墩梁相对位移,又能控制相应桥墩地震剪力的增幅处于合理范围。
4.3 不同温度条件下有限元模型的地震响应分析为了研究温度变化对于全桥有限元模型地震响应的影响,本节针对工况2和工况3~6中不同温度条件建立相应有限元模型并进行输入地震波时程分析。根据《城市桥梁抗震设计规范》规定,时程分析的最终结果,当采用3组地震加速度时程计算时,应取各组计算结果的最大值[16]。相比较于地震波A和C,在地震波B输入下,有限元模型的各墩位移、剪力值均较大,因此本文取地震波B输入下的时程分析结果。
提取2#和7#墩处拉索减震支座的位移值(即支座所发生的剪切变形值)列入表 3中进行对比分析。在表 3中,支座初始位移是由不同温差所引起的,而正向位移与反向位移为支座在地震作用下发生的附加位移,拉索支座的实际位移为初始位移与附加位移之和。位移量的正值表示由2#墩指向7#墩的顺桥方向,负值为反方向。例如,2#支座在-6 ℃时的初始位移值为6 cm,方向为由2#墩指向7#的正方向。
| 温度/℃ | -6 | 4 | 14 | 24 | 34 | |
| 2#支座 | 初始位移/cm | 6.00 | 3.00 | 0.00 | -3.00 | -6.00 |
| 正向位移/cm | 13.19 | 15.67 | 18.12 | 14.41 | 10.63 | |
| 反向位移/cm | -10.94 | -14.29 | -18.16 | -15.81 | -13.12 | |
| 7#支座 | 初始位移/cm | -9.00 | -4.50 | 0.00 | 4.50 | 9.00 |
| 正向位移/cm | 13.20 | 15.69 | 18.14 | 14.48 | 10.61 | |
| 反向位移/cm | -10.91 | -14.31 | -18.05 | -15.83 | -13.14 | |
与此同时,对于不同温度条件下,各墩所承受的最大地震剪力值也是桥梁结构抗震分析中的关注重点。提取各墩在地震波输入下的最大地震剪力值列入表 4中,表中的最大地震剪力值是指桥梁地震往复作用下,沿正反两个方向的最大剪力值之中的较大值。
| 温度/℃ | -6 | 4 | 14 | 24 | 34 | |
| 最大剪力/kN | 2#墩 | 42 725 | 40 736 | 37 360 | 40 811 | 42 366 |
| 7#墩 | 45 513 | 40 012 | 36 202 | 40 516 | 44 257 | |
由表 3可知,当斜拉桥的结构震时温度为14 ℃时,2#支座和7#支座的实际位移量(初始位移+附加位移)分别为18.16 cm和18.14 cm,基本为协同变形,且均超过支座的设计自由程15 cm。这证明拉索已经发挥限位作用,主梁与桥墩之间仅发生约3 cm 的超自由程位移。表 3中表明,此温度下2#墩与7#墩所承担的地震剪力基本保持一致,结构受力相对较为合理。
当温度上升时,梁体伸长引起2#墩与7#墩的拉索减震支座发生偏离固定墩的初始剪切变形,且由于7#墩到固定墩的距离更大,7#支座的初始位移量也较2#支座更大。
以沿正方向的受力情况为例,当温度上升至24 ℃ 时,7#墩处拉索减震支座沿发生共18.98 cm的实际最大位移,超自由程位移为3.98 cm,相应7#墩所受剪力也较14 ℃时有明显提高。此时2#支座的实际最大位移不足15 cm,即支座拉索处于自由程范围内,未能发挥作用。因此2#墩所承担地震剪力较小,更多的地震剪力由7#墩承担,这对桥梁各墩协同受力不利。当温度上升至34 ℃时,7#支座发生19.61 cm的实际最大位移,7#墩所承担的剪力进一步增大,结构受力更加不利。
当温度下降时,梁体收缩导致各墩的支座发生趋向固定墩的初始剪切变形。若仍以沿正方向的受力情况而言,2#墩受力情况变得不利。由表格中数值可看出,当温度下降至4 ℃,2#支座的实际最大位移为18.67 cm,超出自由程3.67 cm,而7#支座的实际位移只有11.19 cm,这就会导致2#墩承担的剪力过大,而7#墩抗剪能力仍有较大富余的情况。当温度下降至-6 ℃时,2#支座剪切变形增至19.19 cm,2#墩受力情况更为不利。
同样,若以反方向受力情况为例,能够得出类似的结果。
5 结论(1)在斜拉桥塔、梁之间设置拉索减震支座能够在小幅度提高墩底剪力的前提下有效减小地震作用下塔、梁之间的相对位移。在斜拉桥抗震设计中,通过拉索刚度、自由程等关键参数的设计,能达到减小位移与增加墩底剪力之间的合理平衡。
(2)采用拉索减震支座的斜拉桥在合龙后,温度变化会引起主梁变形,进而使支座发生初始位移。这种初始位移改变了拉索减震的实际自由程,会出现一部分桥墩在地震作用下承受剪力过大,而另一部分桥墩未充分发挥抗剪作用的不利情况。结构震时温度与合龙温度相差越大,地震剪力在各桥墩上的分配变得越不均衡,部分桥墩受力不利的情形亦越严重。
(3)本文所研究的年温差效应对斜拉桥抗震性能的影响,对于长联多跨桥梁都具有一定参考意义。同时,混凝土收缩、徐变效应所引起的梁体变形可与年温差效应进行叠加考虑。
| [1] | 范立础. 桥梁抗震[M]. 上海:同济大学出版社,1997:281-305. FAN Li-chu. Bridge Seismic Resistance[M]. Shanghai:Tongji University Press,1997:281-305. |
| [2] | 叶爱君,管仲国. 桥梁抗震[M].2版. 北京:人民交通出版社,2011. YE Ai-jun,GUAN Zhong-guo. Bridge Seismic Resistance[M]. 2nd ed. Beijing:China Communications Press,2011. |
| [3] | PRIESTLEY M J N, SEIBLE F,CALVI G M. Seismic Design and Retrofit of Bridges[M]. New York:John Wiley and Sons,1996. |
| [4] | 彭天波,李建中,范立础. 双曲面球型减隔震支座的开发及应用[J]. 同济大学学报:自然科学版,2007,35(2):176-180. PENG Tian-bo,LI Jian-zhong,FAN Li-chu. Development and Application of Double Spherical Aseismic Bearing[J]. Journal of Tongji University:Natural Science Edition,2007,35 (2):176-180. |
| [5] | ZANARDO G,HAO H,MODENA C. Seismic Response of Multi-span Simply Supported Bridges to a Spatially Varying Earthquake Ground Motion[J]. |
| [6] | SOYLU K. Comparison of Random Vibration Methods for Multi-support Seismic Excitation Analysis of Long-span Bridges[J]. |
| [7] | JTG D60—2004,公路桥涵设计通用规范[S]. JTG D60—2004,General Code for Design of Highway Bridges and Culverts[S]. |
| [8] | TG/T B02—01—2008,公路桥梁抗震设计细则[S]. TG/T B02—01—2008,Guidelines for Seismic Design of Highway Bridges[S]. |
| [9] | CJJ 166—2011,城市桥梁抗震设计规范[S]. CJJ 166—2011,Code for Seismic Design of Urban Bridges[S]. |
| [10] | 胡紫东, 李黎,聂肃非. 考虑温度相关性的LRB隔震桥梁地震响应分析[J].振动与冲击,2011,30(9):40-45. HU Zi-dong,LI li,NIE Su-fei. Seismic Response of Isolated Bridges Considering Temperature Effect[J]. Journal of Vibration and Shock,2011,30 (9):40-45. |
| [11] | 袁万城,王斌斌. 拉索减震支座的抗震性能分析[J]. 同济大学学报:自然科学版,2011,39(8):1126-1131. YUAN Wan-cheng,WANG Bin-bin. Numerical Model and Seismic Performance of Cable-sliding Friction Aseismic Bearing[J]. Journal of Tongji University:Natural Science Edition,2011,39 (8):1126-1131. |
| [12] | 韦正华. 拉索减震支座开发及在桥梁抗震中的应用研究[D]. 上海:同济大学,2011. WEI Zheng-hua. Development of Cable Sliding Friction Aseismic Bearing and Its Application in Bridge Seismic Design[D]. Shanghai:Tongji University,2011. |
| [13] | 袁万城, 曹新建,荣肇骏. 拉索减震支座的开发与实验研究[J]. 哈尔滨工程大学学报,2010,31 (12):1593-1600. YUAN Wan-cheng,CAO Xin-jian,RONG Zhao-jun. Development and Experimental Study on Cable-sliding Friction Aseismic Bearing[J]. Journal of Harbin Engineering University,2010,31 (12):1593-1600. |
| [14] | 胡方健,陆元春,张晓松. 南昌市朝阳大桥通航孔桥结构体系研究与设计[J]. 中国市政工程,2014 (1):82-84. HU Fang-jian,LU Yuan-chun,ZHANG Xiao-song. Structural System Research & Design of Navigable Span of Chaoyang Bridge in Nanchang[J]. China Municipal Engineering,2014 (1):82-84. |
| [15] | 余钱华,夏培华,宋泽冈. 大跨长联预应力混凝土连续梁桥地震响应[J]. 重庆交通大学学报:自然科学版,2009,28 (1):1-4. YU Qian-hua,XIA Pei-hua,SONG Ze-gang. Seismic Response of the Large Span Prestressed Concrete Continuous Girder Bridge[J]. Journal of Chongqing Jiaotong University:Natural Science Edition,2009,28 (1):1-4. |
| [16] | 肖星星. 年温差对多跨长联桥的影响分析[J]. 合肥工业大学学报:自然科学版,2008,31(4):639-644. XIAO Xing-xing. Analysis of Influence of the Annual Temperature Difference on the Multi-span Continuous Girder[J]. Journal of Hefei University of Technology:Natural Science Edition,2008,31(4):639-644. |
 2015, Vol. 32
2015, Vol. 32
