扩展功能
文章信息
- 蒋田勇, 龙伟
- JIANG Tian-yong, LONG Wei
- 基于层次分析的石拱桥技术状况评定方法
- A Method for Evaluating Technical Condition of Stone Arch Bridge Based on AHP
- 公路交通科技, 2015, Vol. 32 (9): 49-56
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 32 (9): 49-56
- 10.3969/j.issn.1002-0268.2015.09.009
-
文章历史
- 收稿日期: 2014-08-15
在20世纪七八十年代,我国修建的大量石拱桥经过几十年的运营使用和自然环境侵蚀后,其安全性能受到了很大的影响。随着我国交通量的不断增加,荷载等级不断提高等,大量在役石拱桥的技术状况评定成为一个迫切需要解决的问题[1]。《公路桥涵养护规范》(JTG H11—2004)[2](以下简称《养护规范》)是我国进行石拱桥结构养护和技术状况评定的主要依据,但该规范未根据桥型将部件进行细化[3],以及采用固定的权重分配方式,与工程实际情况存在偏差,使其难以得到科学精确的评估结果[4]。《公路桥梁技术状况评定标准》(JTG /TH21—2011)[5](以下简称《评定标准》)作为现有公路桥梁技术状况评定的重要依据,仍存在工作量大、受评估人员主观影响大等不足之处,有待于在生产实践中进一步完善。
层次分析法的理论结构是这一方法的创始人 T.L.Saaty 教授于1980年在其著作《层次分析法》确立的。潘黎明、史家钧将层次分析法、模糊数学理论应用于进行桥梁安全评价[6];翁艳提出将层次分析应用到混凝土斜拉桥状态评估[7];郭大进、宋波等将层次分析法综合评估在役梁桥养护状况[8]。层次分析法在各国的许多领域都得到了广泛的应用,特别受到欧美国家的青睐。而目前将层次分析法应用于拱桥评定特别是石拱桥的文献十分缺少,本文提出将层次分析法应用于石拱桥的评定,通过算例对3种方法进行对比研究,验证了该方法在石拱桥技术状况评定的可行性和优越性。
1 基于层次分析的技术状况评定方法基于层次分析的评定方法的特点主要体现在构件评定和桥梁部件权重等2个方面,其他环节与《评定标准》的评定相同。
1.1 桥梁构件的技术状况评定针对《评定标准》在桥梁构件病害扣分过程中存在不确定和偏保守等问题,此方法建立了考虑构件不同影响的权重关系的病害扣分叠加公式,并在构件评定过程中考虑恶化系数。
不同病害对同一构件的影响或者不同病害对同一构件的恶化贡献是不相同的,故可运用层次分析法计算其各自对于构件评定的影响权重,将这一不同影响数字化,拟采用以下方法进行叠加。
选择桥梁构件发生的一个最严重病害,即扣分最高的病害,若存在相同扣分,选择最高扣分中权重最大的作为基础扣分,其余病害则考虑对剩余分数的贡献进行扣分叠加,其余病害各自贡献以相对权重为依据。例如:某桥梁构件可能发生A,B,C,D,E 5类病害,假设其各自的影响权重和相应的单项扣分如表 1所示。
| 病害 | A | B | C | D | E |
| 权重 | Wa | Wb | Wc | Wd | We |
| 单项得分DPx | Ua | Ub | Uc | Ud | 0 |
| 注:表中权重存在Wa+Wb+Wc+Wd+We=1的关系,各病害扣分Ui参考《养护规范》中的定性、定量描述进行 | |||||
先假设病害A扣分最多,则以病害A为基础,该构件最终得分为:
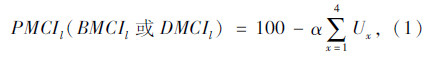
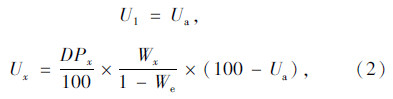
将桥梁的整体结构划分为上部结构、下部结构和桥面系,以石拱桥为例,详细研究基于层次分析的桥梁部件权重的计算步骤。
(1) 明确目标问题同时选定反映问题的指标因素,理清目标问题的目标、要求、范围和所能收集到的基本信息[7]。
(2) 递阶层次评估结构模型建立,见图 1。
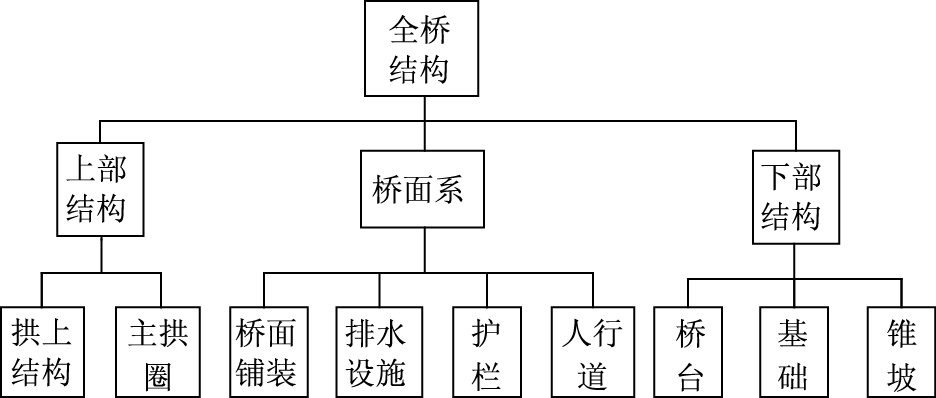
|
| 图 1 桥梁部件评定模型结构图 Fig. 1 Sstructure of bridge comporent evaluation model |
(3) 构造各层的判断矩阵
通过比较分析《养护规范》推荐的部件权重值之间的重要性来构造合适的判断矩阵,其具体步骤如下:
首先,根据各元素的相对重要性比较,在同一层次上将其赋予1~9级定量的若干等级,数值越大表示越重要,反之不重要,则用相应的倒数表示;然后建立两两比较判断矩阵,如表 2所示。
| 乙因素 | 甲因素 | ||||
| B1 | B2 | B3 | … | Bn | |
| B1 | b11 | b12 | b13 | … | b1n |
| B2 | b21 | b22 | b21 | … | b2n |
| B3 | b31 | b32 | b33 | … | b3n |
| | | | | | |
| Bn | bn1 | bn2 | bn3 | … | bnn |
判断矩阵B具有如下性质(一致性条件):
(a) bii=1,其中i=1,2,…,n;
(b) bij=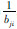 ,其中i,j=1,2,…,n,i≠j ;
,其中i,j=1,2,…,n,i≠j ;
(c) bij×bjk=bik,i,j=1,2,…,n,i≠j。
(4) 单一元素相对权重的计算
得到判断矩阵B后,对矩阵B进行特征根求解

(a) 对矩阵B的各列元素归一化处理;
(b) 归一化完成后对各列进行求和;
(c) 正规化处理得到权重向量ω,其计算公式为:
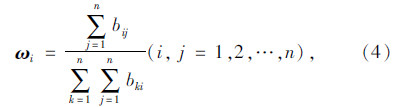
(d) 计算特征值λmax
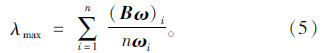
(5) 对判断矩阵B进行一致性检验
矩阵一致性检验需计算一致性检验指标CI、一致性指标RI和相对指标CR这3个指标。
(a) 一致性指标CI
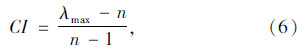
(b) 求解随机平均一致性指标RI
随机平均一致性指标RI是多次(500次以上)重复进行随机判断矩阵特征值计算以后取算术平均得到的。表 3列举了通过1 000次重复计算得到的1~10阶指标取值[10]。
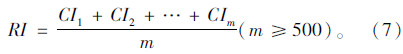
| 矩阵阶数n | 1 | 2 | 3 | 4 | 5 |
| RI | 0 | 0 | 0.58 | 0.89 | 1.12 |
| 矩阵阶数n | 6 | 7 | 8 | 9 | 10 |
| RI | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 |
(c) 求解相对指标CR
判断矩阵一致性随CR的变小而越好,判断矩阵的一致性要求是相对指标CR=CI/RI<0.1,否则需重新构造判断矩阵,即对判断矩阵中的因子作适当调整,直到矩阵B通过一致性检验。
1.3 层次分析法的群组判断建立的判断矩阵若完全依靠某个专家的意见进行计算并不能很好地反映该问题的客观性,因此邀请多位专家参与评定工作,避免个人主观态度引起的判断误差。采用具体的权重反映专家的水平高低,反映各自对目标问题认识的重要性,提高评定的准确性。若某个专家的矩阵计算结果与其他专家的普遍水平较接近,那么这位专家的可信度就越高,其对权重的影响越大。因此,将计算结果的差异性与相似性结合起来,以得到较准确的权重。
(1) 计算专家的相似性
通过计算向量夹角来反映专家评定结果的相似性,相似程度随夹角的变小而增大。假设向量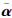 和
和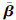 为n维向量,假定其夹角为θ,并定义η为两向量的几何相似性系数。
为n维向量,假定其夹角为θ,并定义η为两向量的几何相似性系数。

将m个专家构造的判断矩阵改写成m个行向量形式,即α1,α2,α3,…,αm,令ηij表示αi和αj的空间夹角的余弦[11],即几何相似系数,令

该式可以用来表示第i个专家的评定判断结果的可信度高低,几何意义是向量αi与其他向量的相似性之和,其值越大则可信度越高。对ηi进行归一化,用ui描述第i个专家与其他专家的评定相似度。
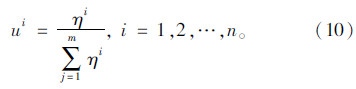
(2) 计算判断差异性
第k位专家对n个判断指标所作的评判值用专家构造的判断矩阵转化成对应的行向量α1,α2,α3,…,αn,αk=(αk1,αk2,αk3,…,αk)来表示,设ei为所有专家对第i个评定指标所作评判值的均值:
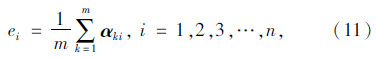
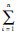 σki(k=1,2,…,m) 表示第k个专家对各个评判指标的评判值与对应评判值的均值的差值总和。
σki(k=1,2,…,m) 表示第k个专家对各个评判指标的评判值与对应评判值的均值的差值总和。
令
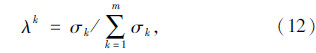
(3) 群组判断中可信度的计算
将专家评判差异性与相似性作为可信度计算的2个变量。先假设用ωk表示第k个专家的可信度,则当 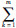 ukλk≠1,
ukλk≠1,

某桥修建于1970年10月,1孔(18.1+2×2.5)m的石拱桥,桥长36.1 m,净矢跨比,F0/L0=1/3,桥宽5.55 m,设计荷载为汽车—15级、挂—80;主拱圈厚0.45 m,为等截面圆弧线线形;两岸桥台采用圬工砌体结构。在现场对该桥上部桥面系、拱圈以及下部台身等主要承重结构进行了详细的观测和调查,认为该桥上部主体结构拱圈轻微损伤,存在涂层脱落、侧墙开裂、桥面破损、混凝土面层破损、使桥头两端存在轻微跳车、两侧桥栏杆破损和桥台锥坡冲空等现象。
2.2 按《养护规范》评定采用《养护规范》中的评定方法,根据某石拱桥的外观检查结果,其技术状况评定结果见表 4。
| 部件编号 | 部件名称 | 权重Wi | 缺损状况 | 影响程度 | 发展变化 | Ri | RiWi |
| 1 | 翼墙、耳墙 | 1 | 0 | — | — | 0 | 0 |
| 2 | 锥坡、护坡 | 1 | 1 | 1 | -1 | 1 | 1 |
| 3 | 桥台及基础 | 23 | 1 | 0 | 0 | 1 | 23 |
| 4 | 桥墩及基础 | 24 | 0 | — | — | 0 | 0 |
| 5 | 地基冲刷 | 8 | 1 | — | — | 0 | 0 |
| 6 | 支座 | 3 | 0 | — | — | 0 | 0 |
| 7 | 上部主要承重构件 | 20 | 1 | 1 | 0 | 2 | 40 |
| 8 | 上部一般承重构件 | 5 | 1 | 1 | 0 | 2 | 10 |
| 9 | 桥面铺装 | 1 | 0 | — | — | 0 | 0 |
| 10 | 桥头与路堤连接部 | 3 | 1 | 1 | -1 | 1 | 3 |
| 11 | 伸缩缝 | 3 | 1 | 1 | 1 | 3 | 9 |
| 12 | 人行道 | 1 | 1 | 1 | 0 | 2 | 2 |
| 13 | 栏杆、护栏 | 1 | 0 | — | — | 0 | 0 |
| 14 | 灯具、标志 | 1 | 0 | — | — | 0 | 0 |
| 15 | 排水设施 | 1 | 2 | 1 | 0 | 3 | 3 |
| 16 | 调治构造物 | 3 | 0 | — | — | 0 | 0 |
| 17 | 其他 | 1 | 1 | 1 | 0 | 2 | 2 |
由表 4计算,该桥技术状况评分得分

根据对某桥的外观检查及专项检查,按照《评定标准》中病害的定性定量描述,对该桥的进行权重重分配[13],各构件扣分结果见表 5~表 7。
| 序号 | 评价部件 | 权重 | 分配后权重 | DCCIi | DCCIi×Wi |
| 1 | 桥面铺装 | 0.40 | 0.421 | 85 | 35.78 |
| 2 | 人行道 | 0.10 | 0.105 | 80 | 8.40 |
| 3 | 栏杆、护栏 | 0.10 | 0.105 | 80 | 8.40 |
| 4 | 排水系统 | 0.10 | 0.105 | 50 | 5.25 |
| 5 | 伸缩缝装置 | 0.25 | 0.264 | 80 | 21.12 |
| 6 | 照明装置 | 0.05 | — | 0 | 0 |
| BDCI | 78.96 | ||||
| 序号 | 评价部件 | 权重 | 分配后权重 | PCCIi | PCCIi×Wi |
| 1 | 主拱圈 | 0.7 | 0.78 | 85 | 66.3 |
| 2 | 拱上结构 | 0.2 | 0.22 | 75 | 15.84 |
| 3 | 桥面板 | 0.1 | — | 0 | 0 |
| SPCI | 82.14 | ||||
| 序号 | 评价部件 | 权重 | 分配后权重 | BCCIi | BCCIi×Wi |
| 1 | 锥坡、护坡 | 0.01 | 0.02 | 70 | 14.00 |
| 2 | 桥台 | 0.30 | 0.45 | 75 | 33.75 |
| 3 | 墩台基础 | 0.28 | 0.42 | 70 | 29.40 |
| 4 | 河床 | 0.07 | 0.11 | 80 | 8.80 |
| 5 | 翼墙、耳墙 | 0.02 | — | 0 | 0 |
| 6 | 桥墩 | 0.30 | — | 0 | 0 |
| 7 | 调治构造物 | 0.02 | — | 0 | 0 |
| SBCI | 75.15 | ||||
桥梁技术状况评分:
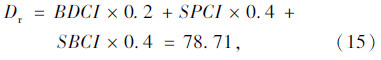
(1) 桥梁各部件权重计算
按层次分析法计算原理,对3位专家进行调差,填写该桥各部件两两比较区间判断矩阵,如表 8~表 10所示。
| 部件 | 桥面铺装 | 护栏、栏杆 | 排水系统 | 河床 | 主拱圈 | 拱上结构 | 锥坡 | 桥台 | 基础 |
| 桥面铺装 | 1 | 3 | 3 | 6 | 1/7 | 1/2 | 7 | 1/2 | 1 |
| 护栏、栏杆 | 1/3 | 1 | 3 | 3 | 1/6 | 1/5 | 2 | 1/5 | 1/4 |
| 排水系统 | 1/3 | 1/3 | 1 | 4 | 1/8 | 1/4 | 1/3 | 1/5 | 1/3 |
| 人行道 | 1/6 | 1/3 | 1/4 | 1 | 1/9 | 1/4 | 1/3 | 1/8 | 1/7 |
| 主拱圈 | 7 | 6 | 8 | 9 | 1 | 4 | 7 | 3 | 4 |
| 拱上结构 | 2 | 5 | 4 | 4 | 1/4 | 1 | 5 | 1 | 2 |
| 锥坡 | 1/7 | 1/2 | 3 | 3 | 1/7 | 1/7 | 1 | 1/3 | 1/3 |
| 桥台 | 2 | 5 | 5 | 8 | 1/3 | 1/3 | 3 | 1 | 1/2 |
| 基础 | 1 | 4 | 3 | 7 | 1/4 | 1/4 | 3 | 2 | 1 |
| 部件 | 桥面铺装 | 护栏、栏杆 | 排水系统 | 河床 | 主拱圈 | 拱上结构 | 锥坡 | 桥台 | 基础 |
| 桥面铺装 | 1 | 4 | 2 | 7 | 1/8 | 1/3 | 5 | 1/4 | 1/2 |
| 护栏、栏杆 | 1/4 | 1 | 5 | 4 | 1/4 | 1/7 | 3 | 1/7 | 1/4 |
| 排水系统 | 1/2 | 1/5 | 1 | 4 | 1/7 | 1/5 | 1/4 | 1/5 | 1/5 |
| 人行道 | 1/7 | 1/4 | 1/4 | 1 | 1/9 | 1/5 | 1/3 | 1/7 | 1/7 |
| 主拱圈 | 8 | 4 | 7 | 9 | 1 | 3 | 8 | 3 | 5 |
| 拱上结构 | 3 | 7 | 5 | 5 | 1/3 | 1 | 5 | 1/2 | 2 |
| 锥坡 | 1/5 | 1/3 | 4 | 3 | 1/8 | 1/7 | 1 | 1/6 | 1/2 |
| 桥台 | 4 | 7 | 5 | 7 | 1/3 | 1/3 | 3 | 1 | 3 |
| 基础 | 2 | 4 | 5 | 7 | 1/5 | 1/4 | 3 | 1/3 | 1 |
| 部件 | 桥面铺装 | 护栏、栏杆 | 排水系统 | 河床 | 主拱圈 | 拱上结构 | 锥坡 | 桥台 | 基础 |
| 桥面铺装 | 1 | 4 | 4 | 5 | 1/5 | 1/4 | 5 | 1/4 | 1/3 |
| 护栏、栏杆 | 1/4 | 1 | 3 | 5 | 1/2 | 1/6 | 5 | 1/5 | 1/4 |
| 排水系统 | 1/4 | 1/3 | 1 | 2 | 1/8 | 1/6 | 1/3 | 1/6 | 1/4 |
| 人行道 | 1/5 | 1/5 | 1/2 | 1 | 1/8 | 1/4 | 1/4 | 1/7 | 1/5 |
| 主拱圈 | 5 | 2 | 8 | 8 | 1 | 5 | 8 | 2 | 6 |
| 拱上结构 | 4 | 6 | 6 | 4 | 1/5 | 1 | 7 | 4 | 4 |
| 锥坡 | 1/5 | 1/5 | 3 | 4 | 1/8 | 1/7 | 1 | 1/5 | 1/4 |
| 桥台 | 4 | 5 | 6 | 7 | 1/2 | 1/4 | 5 | 1 | 2 |
| 基础 | 3 | 4 | 4 | 5 | 1/6 | 1/4 | 4 | 1/2 | 1 |
(a) 权重计算以专家1为例进行说明
第1步,按列归一化,得到:

第2步,各列相加,得到:
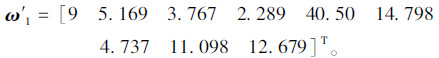
第3步,将行和向量除以向量的代数和,得到:
ω1=[0.087 0.05 0.036 0.022 0.3890.142 0.044 0.107 0.123]T。
第4步,用和法计算判断矩阵最大特征值

第5步,权重一致性检验
当n=9时,RI=1.46
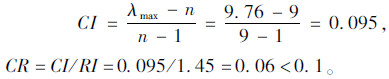
用和法计算后,得出3位专家各自计算结果见表 11。
| 部件权重 | 专家1 | 专家2 | 专家3 |
| 桥面铺装 | 0.09 | 0.07 | 0.08 |
| 护栏、栏杆 | 0.05 | 0.06 | 0.05 |
| 排水系统 | 0.04 | 0.04 | 0.05 |
| 人行道 | 0.02 | 0.02 | 0.03 |
| 主拱圈 | 0.39 | 0.35 | 0.29 |
| 拱上结构 | 0.14 | 0.15 | 0.18 |
| 锥坡 | 0.04 | 0.05 | 0.05 |
| 桥台 | 0.11 | 0.18 | 0.16 |
| 基础 | 0.12 | 0.10 | 0.11 |
| 一致性指标 | 0.062 | 0.081 | 0.072 |
3位专家一致性均满足要求。
(b) 专家可信度计算
将表 12中3位专家的计算结果写成行向量形式:
A={0.09,0.05,0.04,0.02,0.39,0.14,0.04,0.11,0.12},
B={0.07,0.06,0.04,0.02,0.35,0.15,0.05,0.18,0.10},
C={0.08,0.05,0.05,0.03,0.29,0.18,0.05,0.16,0.11}。
| 部件 | 桥面铺装 | 护栏、栏杆 | 排水系统 | 人行道 | 主拱圈 | 拱上结构 | 锥坡 | 桥台 | 基础 |
| 权重 | 0.08 | 0.05 | 0.04 | 0.02 | 0.34 | 0.16 | 0.05 | 0.15 | 0.11 |
运用式(8),计算得:
ηAB=0.982 1,ηAC=0.967 8,ηBC=0.989 1。
运用式(9),计算几何相似系数为:
ηA=0.949 9,
ηB=0.971 2,
ηC=0.956 9。
运用式(10),计算专家相似程度为:
μA=0.330,
μB=0.338,
μC=0.332,
即3位专家的相似度为:
μ3={0.330,0.338,0.332}。
运用式(10)~式(12),计算3位专家差异度为:
λ3={0.353,0.306,0.341}。
将μ3和λ3的值代入式(13),可以计算出3位专家的可信度:
ω={0.320,0.352,0.328}。
通过计算所得专家可信度,采用加权平均的方法对3位专家的评判结果进行汇总,计算的桥梁部件对应权重见表 12。
(2) 各部件底层指标(病害)权重计算
部件底层指标(病害)权重的计算仍采用上述层次分析法进行计算,以某石拱桥为例,表 13~表 16示出主拱圈、拱上结构、基础及桥面系的底层指标权重,其余部件底层指标权重不以表格形式示出。
| 缺损类型 | 变形 | 裂缝 | 渗水 | 拱脚功能受损 | 拱脚位移 | 蜂窝麻面 | 剥落掉角 | 空洞孔洞 | 保护层厚度 | 钢筋锈蚀 | 碳化 | 强度 |
| 评定类别 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 1 | 2 | 1 | 1 | 1 |
| 扣分值 | 0 | 0 | 0 | 0 | 0 | 20 | 25 | 0 | 20 | 0 | 0 | 0 |
| 底层指标权重 | 0.19 | 0.24 | 0.04 | 0.10 | 0.12 | 0.03 | 0.04 | 0.03 | 0.03 | 0.06 | 0.05 | 0.07 |
| 恶化系数 | 0.8 | |||||||||||
| PMCI | 100-0.8×(25+20/100×0.03/1.0×75+20/100×0.03/1×75)=79.28 | |||||||||||
| 缺损类型 | 侧墙与拱圈脱裂 | 侧墙 变形 | 填料沉陷开裂 | 腹拱变形 | 立墙 倾斜 | 表面 缺陷 | 拱上结构裂缝 | 填料排水 |
| 评定类别 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 |
| 扣分值 | 0 | 0 | 0 | 0 | 0 | 20 | 25 | 20 |
| 底层指标权重 | 0.11 | 0.18 | 0.04 | 0.12 | 0.17 | 0.04 | 0.28 | 0.04 |
| 恶化系数 | 1.0 | |||||||
| PMCI | 100-1.0×(25+20/100×0.04/0.36×75+20/100×0.04/0.36×75)=71.67 | |||||||
| 缺损类型 | 冲刷 | 剥落、露筋 | 冲蚀 | 河底铺砌损坏 | 沉降 | 滑移 | 裂缝 |
| 评定类别 | 2 | 1 | 2 | 2 | 1 | 1 | 1 |
| 扣分值 | 25 | 0 | 20 | 20 | 0 | 0 | 0 |
| 底层指标权重 | 0.12 | 0.04 | 0.08 | 0.03 | 0.26 | 0.28 | 0.21 |
| 恶化系数 | 1.0 | ||||||
| PMCI | 100-1.0×(25+20/100×0.08/0.23×75+20/100×0.03/0.23×75)=67.83 | ||||||
| 缺损类型 | 磨光、脱皮、露骨 | 错台 | 坑洞 | 剥落 | 拱起 | 接缝料破坏 | 裂缝 |
| 评定类别 | 1 | 1 | 2 | 2 | 1 | 1 | 1 |
| 扣分值 | 0 | 0 | 25 | 20 | 0 | 0 | 0 |
| 底层指标权重 | 0.08 | 0.16 | 0.17 | 0.08 | 0.17 | 0.14 | 0.20 |
| 恶化系数 | 1.0 | ||||||
| PMCI | 100-1.0×(25+20/100×0.08/0.33×75)=70.2 | ||||||
经计算得出:主拱圈评定得分为79.28分,拱上结构得分为71.67分,基础得分为67.83分,桥面铺装得分为70.2分,1#桥台得分76分,2#桥台得分为100分,锥坡、护坡得分为52分,左侧人行道得分为72分,右侧人行道得分为75分,栏杆得分为80分,防排水系统得分为44.74分。
故该桥全桥技术状况评定Dr=79.28×0.34+71.67×0.16+67.83×0.11+70.2×0.08+76×0.15+52×0.05+72×0.02+80×0.05+44.74×0.04=72.73,属于三类桥,需进行中修。
2.5 3种评定方法的比较按3种方法对该桥进行技术状态评定,将按百分制分别计算桥面系、上部结构、下部结构得分,具体结果见表 17。
| 评定方法 | 《养护规范》 | 《评定标准》 | 层次分析评定方法 |
| 评定结果 | 81.7 (二类) | 78.71 (三类) | 72.73 (三类) |
由上述3种方法的计算结果表明,《养护规范》评定的结果分值最高,《评定标准》评定的结果其次[13],基于层次分析的评定方法评定的结果最低,这主要是由于:
(1)《养护规范》的评定方法未将桥梁部件细化,且将不存在的部件得分考虑为满分,导致桥梁总体技术状况得分较高,评定结果较为粗糙。
(2)《评定标准》评定方法的评定过程较《养护规范》更加细化,故其结果更加接近于桥梁的实际状况,但仍存在将不存在的部件进行权重重分配,受评定人员主观能动性影响大以及工作量大等缺点。
(3) 基于层次分析的评定方法在分析前二者不足之处的基础上,通过充分考虑不存在构件的影响,并采用层次分析方法计算构件不同病害的各自权重,通过权重关系进行叠加扣分,最终得出桥梁总体技术状况,与该桥实际情况更加接近。
3 结论针对大量在役石拱桥的技术状况评定的问题,提出将层次分析法应用于石拱桥的评定,并在桥梁构件的评定和桥梁部件的权重计算等2个方面进行了改进。对于桥梁构件的评定,该方法建立了基于权重的新的病害扣分叠加公式,并在构件评定过程中考虑恶化系数。对于桥梁部件的权重计算,该方法在收集桥梁的基本状况信息基础上,建立了递阶层次评估结构模型,构造了各层的判断矩阵,计算单一元素相对权重,并对判断矩阵进行了一致性检验。研究中还考虑了多个专家的差异性与相似性,确保得到较为准确的权重。以一座石拱桥作为算例进行了详细的研究,结果验证了基于层次分析的技术状况评定方法的可行性和科学性,其相应的研究方法和权重值的计算结果可为目前规范的进一步完善提供依据,为石拱桥的技术状况评定提供参考。
| [1] | 罗阳青.基于模糊层次分析法的服役石拱桥健康评估研究[D].长沙:湖南大学, 2011. LUO Yang-qing. Research on Health Evaluation of in Service Stone Arch Bridge Based on Fuzzy Analytic Hierarchy Process[D]. Changsha:Hunan University, 2011. |
| [2] | JTG H11-2004, 公路养护技术规范[S]. JTG H11-2004, Code of Maintenance of Highway Bridges and Culverts[S]. |
| [3] | 陈栋梁.桥梁技术状况评定方法比较研究[D].重庆:重庆交通大学, 2013. CHEN Dong-liang. Comparitive Study on Technical Condition Evaluation of Bridge[D]. Chongqing:Chongqing Jiaotong University, 2013. |
| [4] | 单德山, 李乔, 徐威.不确定层次分析法在砼桥梁性能评价中的应用[J].重庆交通学院学报, 2007, 26(1):19-22. SHAN De-shan, LI Qiao, XU Wei. Application of the Uncertain Analytical Hierarchy Process to Performance Evaluation of Concrete Bridge[J]. Journal of Chongqing Jiaotong University, 2007, 26(1):19-22. |
| [5] | JTG/TH21-2011, 公路桥梁技术状况评定标准[S]. JTG/TH21-2011, Standards for Technical Condition Evaluation of Highway Bridges[S]. |
| [6] | 潘黎明, 史家钧.桥梁安全性与耐久性综合评估研究[J].上海公路, 1998(1):28-32. PAN Li-ming, SHI Jia-jun. Study of Bridge Safety and Durability Evaluation Methods[J]. Shanghai Highways, 1998 (1):28-32. |
| [7] | 翁艳.基于层次分析法的混凝土斜拉桥状态评估[D].成都:西南交通大学, 2007. WENG Yan. Condition Assessment of Concrete Cable-stayed Bridge Based on Analytic Hierarchy Process[D]. Chengdu:Southwest Jiaotong University, 2007. |
| [8] | 郭大进, 宋波, 周文欢.基于层次分析法的在役梁桥养护状况综合评估[J].公路交通科技, 2011, 28(3):108-111. GUO Da-jin, SONG Bo, ZHOU Wen-huan. Comprehensive Assessment of Maintenance Status of In-service Beam Bridges Based on AHP Theory[J]. Journal of Highway and Transportation Research and Development, 2011, 28(3):108-111. |
| [9] | ALONSO J A, LAMATA M T. Consistency in the Analytic Hierarchy Process:a New Approach[J].International Journal of Uncertainty, Fuzziness and Knowledge-based Systems, 2006, 14(4):445-459. |
| [10] | STANNARD B, ZAHIR S. Application of Analytic Hierarchy Process in Multi-objective Mixed Integer programming for Airlift Capacity Planning[J].Asia-pacific Journal of Operational Research, 2006, 23(1):61-76. |
| [11] | AHMAD N, BERG D, SIMONS G R.The Integration of Analytic Hierarchy Process and Data Envelopment Analysis in a Multi-criteria Decision-making Problem[J].International Journal of Information Technology & Decision Making, 2006, 5(2):263-276. |
| [12] | 范剑锋, 袁海庆, 钟珞.不确定层次分析下的桥梁评估最优指标权重确定[J].公路交通科技, 2007, 24(9):66-68. FAN Jian-feng, YUAN Hai-qing, ZHONG Luo. Determination of the Optimized Index Weights for Bridge Evaluation under Uncertain Hierarchy Analysis[J]. Journal of Highway and Transportation Research and Development, 2007, 24(9):66-68. |
| [13] | 陆进详.《公路桥涵养护规范》与《公路桥梁技术状况评定标准》浅析[J].青海交通科技, 2013(5):18-19. LU Jin-xiang. Brief Analysis on Code of Maintenance of Highway Bridges and Culverts and Standards for Technical Condition Evaluation of Highway Bridges[J].Qinghai Science & Technology of Communications, 2013(5):18-19. |
 2015, Vol. 32
2015, Vol. 32
