扩展功能
文章信息
- 耿丹阳, 郭兰兰, 李博
- GENG Dan-yang, GUO Lan-lan, LI Bo
- 基于复杂网络理论的深圳和东京地铁线网系统对比分析
- Comparative Analysis of Shenzhen and Tokyo Metro Systems Based on Complex Network Theory
- 公路交通科技, 2015, Vol. 31 (8): 126-132
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (8): 126-132
- 10.3969/j.issn.1002-0268.2015.08.021
-
文章历史
- 收稿日期: 2014-02-26
2. 中国交通通信信息中心, 北京 100011;
3. 大连理工大学 交通运输学院, 辽宁 大连 116024
2. China Transport Telecommunications and Information Center, Beijing 100011, China;
3. School of Transportation & Logistics, Dalian University of Technology, Dalian Liaoning 116024, China
复杂网络是指不规则、复杂并随时间变化而变化的网。20世纪末,《自然》和《科学》上的两篇文章分别讨论了小世界网络集体动力学[1]和随机网络规模[2],使复杂网络科学引起广泛关注,掀起了复杂网络的研究热潮。随着城市交通拥堵问题的日渐突显,大力发展公共交通已经成为城市交通发展的趋势。城市轨道交通包括地铁、轻轨、市郊铁路、有轨电车等,是现代大运量交通工具的首选之一,逐渐在世界各大城市的公共交通中处于骨干地位。作为一个实体网络,城市轨道交通建设投资巨大、影响深远,它的规划是一项艰巨复杂的系统工程。因此,利用复杂网络理论分析其网络特性,并以其网络特性为依据对轨道交通线网及其运营进行合理的优化具有非常重要的现实意义。
在国内,许多学者根据轨道交通的网络特性,利用复杂网络理论对其进行了研究。文献[3]对上海轨道网的复杂网络特征进行了探讨,得出上海轨道网在L空间和P空间具有小世界特性和无标度特性。文献[4]基于复杂网络理论对广州轨道交通网络的可靠性进行了研究,发现其呈现随机网络特征。文献[5]对国内包括北京、上海、广州在内的10条地铁线网进行了抗攻击性分析和研究,发现它们普遍呈现易瓦解特征。
文献[6, 7]对世界上较有代表性的33座城市的地铁线网网络特性数据进行了对比和分析。这些研究不仅科学地沿用了公认的、有代表性的网络特性指标来刻画地铁线网,并且结合地铁线网自身的特征衍生出了包括强健性及结构连通性等很有意义的指标。另外,他们对地铁网络状态、形式及结构创造性的刻画,能够更有效地定位地铁发展现状,更有利于指导未来地铁线网规划,进而使地铁网络结构设计达到精准化、有效化和科学化。
本文以文献[6, 7]的理论、模型和方法为依据,深入研究深圳地铁系统的网络构造、分析深圳地铁网络的网络特性指标,并对深圳地铁网络的强健性、结构连通性进行讨论。该分析从深圳地铁的状态、形式和结构方面为深圳地铁网络现状定位及未来发展提供建设性的意见。
1 地铁的网络特性 1.1 地铁的网络化本文将地铁网络抽象为数学网络,即:将地铁站点看作网络节点,将连接两站点间的地铁线看作网络中的边。因本文着眼于网络结构的研究,所以仅考虑转乘站和起终点站(简称为尾站),但在考虑站间距时,会把所有站点考虑进来。其对应的抽象网络只包含每条线的起点、终点以及任一两条线的换乘节点。
假设转乘站数为Vt、尾站数为Ve,V为两者之和。把边分为单线边和复线边两类,单线边指两个节点之间只有1条连接线路;复线边指两个节点之间有两条或两条以上的连接线路。按照文献[7],针对一对节点之间有至少两条线路连接的情况,任选1条归为单线边,剩余的线路统一作为1条复线边处理。那么,所有的边数即为单线边数Ds与复线边数Dm之和,记为D。 1.2 地铁线网的一般网络特性 1.2.1 无标度特性作为描述网络图的一个最基本术语,度代表与一个节点相连接的边的数目。一般而言,一个节点的度越大,它越重要。在现实地铁线网中,为更直观地体现一个站点在整个地铁线网中的重要程度,将度的含义引申为经过一个站点的线路条数[6],例如,若一个站点有两条轨道线路经过,其度为2,而不是4。
网络中节点的度分布可用分布函数p(k)来描述,它表示的是一个随机选定节点的度恰好为k的概率分布。该函数反映网络系统的宏观统计特征。本文用上文度的延伸含义,以p(l)(l指经过一个节点的地铁线路数)来描述一个随机选定站点的度恰好为l的概率分布[8]。大量研究表明,许多地铁网络的度分布p(l)普遍呈现幂律分布[6, 7]:

小世界理论又称为六度分割理论,对它有一个通俗的解释,即:最多通过6个人就能认识任何一个陌生人。Watts和Strogatz将小世界网络定义为满足以下两个规则的网络[6]:
规则1:高的聚类系数;
规则2:小的平均最短路径。
其中,聚类系数反映网络中“三角关系”的密度大小。若一个节点通过ki条边和其他节点相连,通过这ki条边和该节点直接相连的节点称为该节点的邻居。鉴于地铁线网属于平面网络,故潜在的连接边数为3ki-6[6],将实际存在的边数记为ei,则单个节点的聚类系数可定义为:


但对于地铁线网来说,我们更倾向从整体上考虑它的发展程度,即度量它当前的发展程度与该地铁线网潜在的发展程度之间的差距。因此,探讨另一个最初由Garrison和Marble引入交通运输网络中的连接度指标γ[6],它反映的是网络连通程度的大小,计算公式为:

此外,规则2中的平均最短路径在这里指通过最短路径来连接网络中所有节点时所需的最大换乘次数,记为δ。依据小世界特性,这一指标必须低于总站数ns的对数值,即lnns。
1.3 地铁线网的特殊网络特性 1.3.1 强健性强健性在网络研究中尤为重要。当地铁线网遭受突发事件(技术故障、事故以及暴力袭击)时,强健性的大小直接影响到它的应急能力。首先,引入一个中间指标μ,它代表网络中存在的环的数目[6],即:
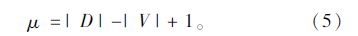
强健性指标rt则是应急通道(网络中的替代线路)与所有潜在意外节点的比值,定义为:

指一个网络的当前发展阶段,可量化为网络复杂度和连接度两个指标。连接度指标γ是上文提到的连接度,该值的大小体现网络的成熟度。复杂度β定义为:

网络形式描述地铁线网如何与城市环境相融合。 地铁线网覆盖范围是不同的。地铁运营可分为3种形式。一是全局型,这种形式的地铁线网线路长、站距较远,主要为市郊居民来往市中心提供服务。二是局域型,它的特点是站距小、线路短,服务于市中心居民日常活动。三是前两种形式的结合,称为混合型,它的线路站距不定。郊区居民出行需求密度小,因而平均站距就适当放大,行车速度相对提高;而在市中心,出行需求密度大,因而平均站距相对小,行车速度相应也会放慢。第3种类型的线网既能较好地服务于市中心,又能服务于郊区居民,能够保证地铁线网的高效率运作。
假定地铁线路数为nl、总站数为ns,总线路长度为L,为更清楚展现这3种形式地铁线网的特点,文献[6]引入两项指标:平均线路长度A和平均站距S:


网络结构直接反映地铁线网设计方案的技术含量,在很大程度上决定了整个城市居民乘坐地铁的方便程度。有两个指标可以体现地铁线网的结构特征:关联度ρ和连通性τ。首先,定义整个网络的总换乘数指标Vct:
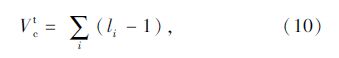
关联度ρ反映网络中所有换乘的可能性,用来有效测量聚焦于结构上的关联度,定义为:
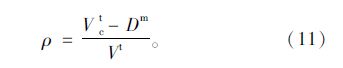

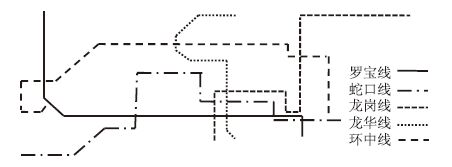
作为我国第1个也可以说是目前发展最成功的一个经济特区,深圳市也是我国除北京和上海外较早建设轨道线网的城市之一。截至2012年底,深圳开通5条轨道线路(图 1),分别为:罗宝线、蛇口线、龙岗线、龙华线、环中线。地铁总里程为178 km,日均客流量超过200万人次。由图 1可导出对应的抽象网络,只包含每条线的起点、终点以及任两条线的换乘节点,这里不再画出。
|
| 图 1 深圳地铁网示意图 Fig. 1 Schematic diagram of Shenzhen metro network |
罗宝线全长23.592 km,从罗湖站至机场东站,呈东西走向。该线连接了深圳市的东门商业区、蔡屋围一带的中央商务区、华强北商业区、深圳市中心区、深圳华侨城的高级住宅区以及深圳的华侨城旅游区。
蛇口线全长20.65 km,从赤湾站始发,经世界之窗站与罗宝线相交,穿越市中心最终到达新秀站,连接南山、福田以及罗湖3个区。
龙岗线由福田区的益田村至龙岗区的双龙,总长约41 km,大运会在深圳举办期间,被誉为“大运专线”,在大运会人员输送方面发挥了重要作用。 龙华线位于深圳市中心区中轴线及金田路底部,从福田口岸站至少年宫站,呈南北走向,全长15.8 km。
环中线贯穿城市第1、第2圈层,连接城市西、中、东3条发展轴,是构成深圳市近中期线网的骨干线路,是联系沿线各组团和3大交通枢纽的快速走廊。环中线全线长为40.001 km。
2.2 深圳地铁网络特性分析东京地铁是世界上公认的发展比较成熟的地铁网,市中心区轨道线网密度高达2.2 km/km2,大都市圈内每km2亦有约200 m线路,其线路长度和线网密度居世界城市之首[9]。相比世界上其他同等规模的轨道线网,东京轨道线网强健性最高,也是发展最为成熟的大型轨道线网之一[5]。它的整个线网结构合理、换乘节点分布广泛,使得各条线路间的换乘相当方便,因而各个地区通过地铁无需使用地面交通的直达性很强。
表 1和表 2分别为深圳与东京地铁的基本参数对照表和两城市地铁网络特征参数对照表。
| 网络基本参数 | 深圳 | 东京 |
| 线路总长/km | 178 | 292.38 |
| 总站点数 | 118 | 202 |
| 线路条数 | 5 | 13 |
| 总节点 | 21 | 61 |
| 尾节点 | 8 | 16 |
| 换乘节点 | 13 | 45 |
| 总边 | 29 | 119 |
| 单线边 | 29 | 111 |
| 复线边 | 0 | 8 |
| 总站点数的对数ln ns | 4.77 | 5.31 |
| 网络特征参数 | 深圳 | 东京 |
| 无标度指标 | 3.01 | 2.80 |
| 连通程度 | 0.51 | 0.67 |
| 强健性 | 0.076 3 | 0.252 5 |
| 复杂性 | 1.38 | 1.95 |
| 平均线路长度/km | 35.6 | 22.49 |
| 平均站距/km | 1.51 | 1.45 |
| 结构连通性 | 1 | 1.29 |
| 最大换乘次数 | 1 | 2 |
| 直通性 | 5 | 6.50 |
(1)无标度特性
无标度特性使得网络对意外故障具有惊人的强健性,被随机破坏去除的主要是那些只拥有少量连接、不重要的节点。随机去除这些交通节点并不会造成整个交通网络的瘫痪,但若蓄意对交通枢纽点进行攻击和破坏,就会迅速导致整个网络瘫痪[10]。
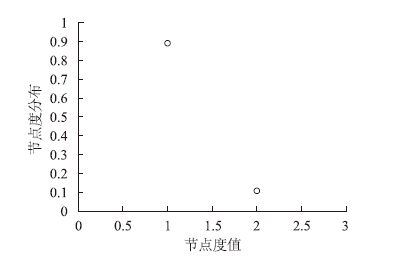
图 2给出了深圳市地铁网节点度值分布的计算结果。可以看出,深圳市地铁网中节点的度最大为2,共11个站点。其中,8个站点分布在市中心,说明它们是地铁网络中最重要的换乘站,另外3个站点分布在不同方位的市郊,也是相当重要的换乘节点。此外,从图 1可以看出,这些换乘站点分布很有规律,保证了每条线路都与其他线路存在换乘站点。可见深圳地铁网的换乘比较方便。 节点度为1的车站所占比例最大,约占82%。这是由于深圳地铁网处于初建阶段,还未发展成为成熟的网络。
|
| 图 2 节点度值分布 Fig. 2 Distribution of values of node degree |
研究证明,许多地铁网络的度分布p(l)普遍呈现幂律分布。因此,本文假设深圳地铁网符合无标度网络特性。根据深圳地铁线网数据进行计算,得出其对应的无标度指标值ε为3.01。深圳市地铁网中大多数的站点只有1条线路通过,少数车站才为换乘站,37.2%的地铁站点与换乘站直接相连。由于无标度网络具备偏好依附性,节点的生长优先连接节点度大的节点。这也说明了这些换乘站在整个深圳地铁网中的重要性。
东京轨道线网的网络化起步早,发展较成熟,呈典型的带环形放射型线网布局,一些大型换乘站与多达10多个站点相连。文献[6]中计算出东京地铁网的无标度特性更加显著,达到了2.8。
(2)小世界特性
网络的小世界特性体现了网络节点连接的紧密性。在地铁网中,小世界特性越明显,站与站之间的连接越紧密。
对小世界网络的高强度聚类性和短特征路径特性,由最大换乘次数σ和连接度γ测量。研究表明,地铁网从小型网络发展成为成熟的大型网络,它的连接度γ将不断地逼近0.66[7]。东京地铁网的γ值已超过0.66,而深圳地铁网的连接度为0.51,也达到了相对较高的水平。对于另外一个指标σ,东京的特征路径为2,即全网的最大转乘次数为2,而深圳地铁线网有一个显著特征,即每两条线路之间都有1个换乘节点,这就保证了它的最大换乘次数仅为1。
(3)强健性
东京地铁网的站点聚类性很高[8],γ达到了0.67;无标度参数指标ε在同规模网络中也是最小的。因此,东京地铁网有很高的强健性。对比发现,深圳地铁网的连接度γ相对较小,无标度指标ε相对较大。由此,它的强健性指标rt仅为0.076 3,远远小于东京地铁网强健性指标值0.252 5。
但是,深圳地铁网的二期建设才刚刚落幕,三期建设正在实施。最初地铁网是着眼于不断建设线路和站点来覆盖交通需求量大的地区。在线路和站点数量限定的条件下,不能创造更多的网络环。因此,强健性并不能得到有效保障。在地铁网络发展壮大的过程中,可以采取一定的建设策略来提高网络的强健性。例如,在扩建地铁网时,可着眼于创造更多的转乘站来形成网络环。网络环可为乘客提供多条替代线路,进而在遇到自然灾害或恶意攻击事件时可有效降低损失。
(4)网络状态
地铁线网存在一个3阶段的发展过程,如表 3所示。可以看出,深圳地铁线网的两个指标值分别为β=1.3和γ=0.5,处于第1阶段,还有很大的发展扩建空间。相比之下,东京地铁网β=1.95,γ=0.67,显然已步入成熟阶段。
| 指标 | 第1阶段 | 第2阶段 | 第3阶段 |
| β | 1.3 | 1.6 | 1.96 |
| γ | 0.5 | 0.6 | 0.7 |
(5)网络形式
每个城市应根据自身特点选择合适的运营形式。深圳地铁属于第3种形式,即:在市中心需求量大的区域,线路覆盖较多,且各条线路有意减小站距,使得站点聚集量较大,可有效地满足市中心的出行需求。而在市郊,适当增大站距以提高车速,既减小了运营成本也提高了运营效率。对应于深圳地铁线网网络形式的两个指标值为:A=35.6 km,S=1.51 km。东京地铁的A和S两个指标都小于深圳。这说明除了在成熟度上存在差异外,深圳地铁线网站点覆盖密集度也逊于东京。
(6)网络结构
深圳地铁网的连通性ρ=1,虽然低于东京的1.29,但已经是一个较好的值。这归因于深圳地铁网络换乘节点的配置。深圳地铁换乘节点较多,各个地区的换乘都很方便,增强了网络可达性。例如,宝安区和盐田区的交通需求都可通过市中心或市郊的换乘节点得到满足。直达性τ=5,也达到了相当满意的水平。深圳地铁网现今运营线路有5条,每两条线路之间都有换乘节点,使得最大换乘次数保持一个很低的值,即σ=1。
一些城市的地铁网设计着重于提高其连通性,另一些则着重提高其直达性,而深圳地铁网则成功实现了两者的共赢。这是我国城市地铁线网结构设计的一个成功案例。
2.3 未来深圳地铁线网评价为了使本文的研究成果有效地指导实践,指导未来深圳市地铁线网建设,下面再对规划的深圳市2020年和2030年地铁线网进行分析[11, 12],计算结果见表 4和表 5。为便于比较,把前面计算的深圳市现状地铁线网的属性值和东京地铁线网的属性值也列在其中。
| 网络基本参数 | 深圳 | 东京 | ||
| 现状 | 2020年 | 2030年 | 现状 | |
| 线路总长/km | 178 | 423.4 | 585.3 | 292.38 |
| 总站点数 | 118 | 226 | 357 | 202 |
| 线路条数 | 5 | 12 | 16 | 13 |
| 总节点 | 21 | 49 | 78 | 61 |
| 尾节点 | 8 | 9 | 11 | 16 |
| 换乘节点 | 13 | 40 | 67 | 45 |
| 总边 | 29 | 86 | 140 | 119 |
| 单线边 | 29 | 83 | 136 | 111 |
| 复线边 | 0 | 3 | 4 | 8 |
| 总站点数的对数ln ns | 4.77 | 5.42 | 5.88 | 5.31 |
| 网络特征参数 | 2020年 | 2030年 |
| 复杂性 | 1.76 | 1.79 |
| 最大换乘次数 | 3 | 3 |
| 无标度指标 | 2.93 | 2.99 |
| 连通程度 | 0.609 9 | 0.614 0 |
| 强健性 | 0.154 9 | 0.165 3 |
| 平均线路长度/km | 35.28 | 36.58 |
| 平均站距/km | 1.87 | 1.64 |
| 结构连通性 | 1.08 | 1.10 |
| 直通性 | 4.00 | 5.33 |
由表 4和表 5可知,到2020年,深圳市将新增地铁线路7条,线路总长将达423.4 km,线网复杂度将从1.38增加到1.76,将跨入地铁网发展的第2阶段。但由于在1号线和3号线的基础上分别延伸出8号线和12号线,以及10号线的存在,使得最大换乘次数增加到3。然而,深圳地铁几乎做到了无缝换乘。因此,换乘次数的增加并不会给乘客带来太多不便。就连通性和强健性而言,相比于现今的地铁线网都有很大提升,但对比东京轨道线网仍有较大差距。深圳地铁线网属于混合型发展模式,其平均线路长度和平均站距都没有较大变化。网络结构的连通性指标只有微小改进。然而,最大换乘次数的增加使得线网直通性下降。可以看出,无标度指标落到2~3之间,说明随着线网规模的扩大,深圳地铁网的无标度特性越加明显。最大换乘数也小于节点的对数值。
2030年的深圳地铁网络比2020年增加4条线路,各项指标值只有小幅提升,而与东京轨道线网数据相比,依然有较大的差距。深圳地铁网依然处于不断建设和完善阶段,即网络发展的第2阶段。因此,相关规划部门应该借鉴东京轨道网的线路规划方案,对未来深圳地铁线网的规划进行适当调整,使得各项指标都达到较高水平。本文认为环线与放射线的适当布设可以多创造线路交叉,使得换乘节点数增加,能够有效优化深圳轨道交通线网的属性。
3 结论基于复杂网络的理论、模型和方法,对比东京地铁线网,深入分析了深圳地铁线网,主要结论有:
(1)深圳地铁线网具有无标度特性和小世界特性,强健性比东京地铁线网还有一些差距。
(2)通过分析网络状态、模式和结构特征,发现目前深圳地铁网处于地铁发展的第1阶段,即初步建设阶段,属于混合运营模式,具有较好的连通性和直达性。
(3)对深圳市未来(2020年和2030年)的规划线网特性的研究表明深圳地铁规划方案比东京轨道现网存在较大差距,建议采用放射线及环线来优化深圳轨道交通线网。
| [1] | WATTS D J, STROGATZ S H. Collective Dynamics of "Small World" Networks[J]. |
| [2] | MARCHIORIA M, LATORA V. Harmony in the Small World[J]. Science, 1999, 285(3/4): 539-546. |
| [3] | 王燚,杨超. 上海市轨道交通网络的复杂网络特性研究[J]. 城市轨道交通研究, 2009,12(2): 33-36. WANG Yi, YANG Chao. Characteristics of the Complex Network in Shanghai Urban Rail Transit[J]. Urban Mass Transit, 2009,12(2): 33-36. |
| [4] | 王云琴.基于复杂网络理论的城市轨道交通网络连通可靠性研究[D].北京:北京交通大学, 2008. WANG Yun-qin. Research on Connectivity Reliability of Urban Rail Transit Network Based on Theory of Complex Network[D].Beijing: Beijing Jiaotong University, 2008. |
| [5] | 刘志谦,宋瑞. 基于复杂网络理论的广州轨道交通网络可靠性研究[J]. 交通运输系统工程与信息, 2010,10(5): 194-200. LIU Zhi-qian, SONG Rui. Reliability Analysis of Guangzhou Rail Transit with Complex Network Theory[J]. Journal of Transportation Systems Engineering and Information Technology, 2010,10(5): 194-200. |
| [6] | 鄢巨平,谭仲平. 日本大都市轨道线网构架分析与思考[J].城市轨道交通研究, 2002,5(1): 92-93. YAN Ju-ping, TAN Zhong-ping. Analysis of the Urban Rail Transit Line and Network in Japan [J]. Urban Mass Transit, 2002,5(1): 92-93. |
| [7] | 苗彦英. 东京城市轨道交通路网分析[J].城市轨道交通研究, 1998,1(2): 66-67. MIAO Yan-ying. The Analysis of Tokyo Urban Rail Transit Network [J]. Urban Mass Transit, 1998,1(2): 66-67. |
| [8] | HAN C F, LIU L. Topological Vulnerability of Subway Networks in China [C]// International Conference on Management and Service Science, 2009. Wuhan: IEEE, 2009: 1-4. |
| [9] | DERRIBLE S, KENNEDY C. The Complexity and Robustness of Metro Networks [J]. |
| [10] | DERRIBLE S, KENNEDY C. Characterizing Metro Networks: State, Form and Structure [J]. |
| [11] | 深圳轨道交通委员会. 远期轨道交通线网方案(至2030年)[EB/OL]. [2007-07-09]http://www.szpl.gov.cn/main/gdgh/. Committee of Shenzhen Subway Administration. Long-term Rail Transit Network Plan (to 2030) [EB/OL]. [2007-07-09]. http://www.szpl.gov.cn/main/gdgh/. |
| [12] | 深圳轨道交通委员会.深圳地铁线路图规划[EB/OL]. [2011-10-28]. http://sz.bendibao.com/sou/? key=%B5%D8%CC%FA%CF%DF%C2%B7%CD%BC. Committee of Shenzhen Subway Administration. The Plan of Shenzhen Subway [EB/OL]. [2011-10-28]. http://sz.bendibao.com/sou/?key=%B5%D8%CC%FA% CF%DF%C2%B7%CD%BC. |
 2015, Vol. 31
2015, Vol. 31
