扩展功能
文章信息
- 唐亮, 张皓, 刘玉擎, 冯清海
- TANG Liang, ZHANG Hao, LIU Yu-qing, FENG Qing-hai
- 协作桥合理成桥状态确定方法研究
- Research on Method for Determining Reasonable Completion State of a Combined Cable-stayed and Suspension Bridge
- 公路交通科技, 2015, Vol. 31 (8): 107-112
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (8): 107-112
- 10.3969/j.issn.1002-0268.2015.08.018
-
文章历史
- 收稿日期: 2014-10-15
2. 中交公路长大桥建设国家工程研究中心有限公司, 北京 100088;
3. 同济大学 土木工程学院, 上海 200092;
4. 云南省交通规划设计研究院, 云南 昆明 650011
2. CCCC Highway Bridges National Engineering Research Centre Co., Ltd., Beijing 100088, China;
3. School of Civil Engineering, Tongji University, Shanghai 200092, China;
4. Yunnan Transportation Planning and Design Institute, Kunming Yunnan 650011, China
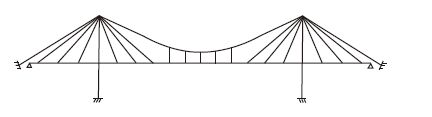
斜拉-悬索协作桥是在传统斜拉桥和悬索桥基础上发展起来的一种组合体系桥梁。中跨跨中部分采用悬索体系,可以解决斜拉体系悬拼过程中的静力稳定、气动稳定和主梁压力过大的问题;借助与斜拉体系的协作,可以提高悬索体系的刚度、降低主缆拉力和锚碇规模,尤其对深水和软土地基情况意义重大[1, 2, 3, 4]。从1883年罗勃林为提高悬索桥的刚度和抗风性能而提出用斜拉索增强悬索体系的构想至今,国内外桥梁工作者提出过多种协作体系形式,其中狄辛格提出的体系得到了较为广泛的认可,如图 1所示,在世界各地筹建的大跨度桥梁方案中被频繁地提出,1997年,由重庆交通学院等单位设计,我国在贵州乌江上建成了跨径为288 m的世界首座斜拉-悬索协作桥,实现了该桥型零的突破[5, 6]。
|
| 图 1 狄辛格体系 Fig. 1 Dischinger system |
在缆索承重桥梁设计中,确定桥梁的成桥状态具有十分重要的意义。目前斜拉桥和悬索桥成桥状态的确定方法已经比较成熟[7, 8],但针对协作桥的研究还十分有限。大连理工大学朱巍志、张哲等人推导了不变形预张力的索力不变原理,利用该原理并结合现有斜拉桥、悬索桥的有关方法,提出了自锚式斜拉-悬索协作桥合理成桥状态确定的分步算法[9]。但其方法针对自锚式协作桥,对最常见的地锚式协作桥的适用性未予讨论,此外其涉及的模型、步骤多,整体较为复杂。
为此,本文以成桥时桥塔和主梁的位移最小为优化目标,以斜拉索初始索力、主梁压重为主要施调变量,提出了一种考虑主要几何非线性效应的协作桥合理成桥状态迭代方法,并以琼州海峡跨海通道的主跨3 000 m协作桥方案为例进行了验证。
1 直接组合法及其不足斜拉-悬索协作桥由斜拉体系和悬索体系相互协作、共同承担作用在主梁上的荷载,对于通常的狄辛格体系协作桥,斜拉体系和悬索体系各司其职,彼此之间影响相对较小。因此,在确定协作桥成桥状态时,最直接的就是将其作为斜拉体系和悬索体系的直接组合,采用目前成熟的方法分别确定两个体系的合理成桥状态,再简单叠加,这就是本文所称的直接组合法。
直接组合法实施步骤如下:
(1)将协作桥全桥模型拆分为悬索体系模型和斜拉体系模型两部分。悬索体系模型只需将全桥模型所有斜拉索单元去掉,并在原有斜拉索相交的主梁节点上施加竖向约束;斜拉体系模型则需将全桥模型中的主缆和吊索单元去掉,并在原有吊索相交的主梁节点上施加竖向约束。对于斜拉索与吊索有交叉的过渡段,首先应确定该区域内主梁恒载在斜拉索和吊索之间的分配比例,然后将对应的荷载以节点力的形式分别施加在悬索体系模型和斜拉体系模型中,过渡段内的主梁不约束节点竖向自由度。
(2)对于悬索体系模型,本文采用文献[10]提出的分段悬链线法反复迭代确定其合理成桥状态。
(3)对于斜拉体系模型,本文采用文献[11]和[12]提出的影响矩阵法及其实用方法,将主梁和桥塔的抗弯刚度减小为1/1 000后,确定其合理成桥状态。
(4)将上述悬索体系和斜拉体系分别确定的主缆初始构形和缆、索初始内力施加至协作桥全桥模型,考虑全几何非线性因素后,计算得到协作桥成桥状态。
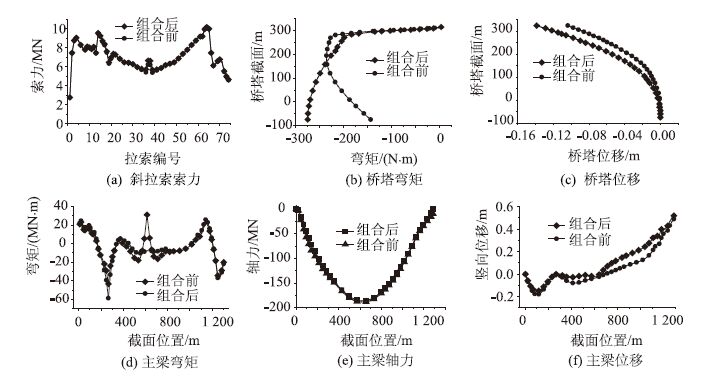
以琼州海峡跨海通道的主跨3 000 m协作桥方案为例,图 2给出了直接组合法计算得到的协作桥成桥状态。由图可见,将悬索体系和斜拉体系组合后,结构的受力状态偏离了二者相互独立时的受力状态,特别是桥塔的位移和弯矩变化明显,组合后的塔顶位移由0.104 m变为0.139 m,塔底弯矩由142 MN·m变为273 MN·m。
|
| 图 2 直接组合法计算结果 Fig. 2 Calculation result of direct combination method |
究其原因,主要是由桥塔的P-Δ效应造成的。在协作桥中,斜拉体系和悬索体系共用桥塔,单独确定斜拉体系合理成桥状态时,并未考虑悬索体系主缆传递给桥塔的荷载。事实上主缆传递给桥塔的压力是非常可观的,本结构中每一侧桥塔需承受主缆传递的竖向力1 311 MN。在单独的悬索体系中,桥塔基本不承受纵桥向荷载,处于单纯受压状态,但在协作桥中,由于斜拉索的不平衡水平力,桥塔存在纵向弯矩和位移,在考虑几何非线性影响的情况下,在塔顶施加主缆传递的巨大竖向力后,P-Δ效应将导致桥塔弯曲变形增大,加上桥塔产生竖向压缩,斜拉索两端点的几何关系将随之改变,从而导致斜拉索的索力发生变化。反过来,桥塔变形导致的塔顶位移也会改变悬索体系的初始成桥状态。因此,分别确定斜拉体系和悬索体系的合理成桥状态,再将二者组合在一起,得到的协作桥成桥状态偏离了预期。
2 确定协作桥成桥状态的迭代法确定协作桥的合理成桥状态,必须综合考虑斜拉体系和悬索体系之间的相互影响,保持桥塔竖直,处于单纯受压状态是关键。
以下提出一种确定协作桥合理成桥状态的迭代法,该方法以成桥时桥塔和主梁的位移最小为优化目标,通过迭代,不断调整斜拉体系主梁配重及斜拉索索力,使成桥时桥塔纵桥向不平衡力及主梁斜拉索锚固点处竖向不平衡力调整至接近于零;同时不断更新悬索体系主缆构形和缆、索内力,使悬索体系主梁竖向位移接近于零。这样成桥时的桥塔将处于单纯受压状态,保持竖直,而主梁位于设计曲线上且内力处于刚性支承连续梁状态。
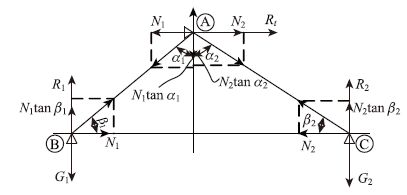
该方法的关键是确定斜拉体系的零位移状态。如图 3所示,考虑锚固在桥塔同一点处的左右两根斜拉索,将其作为一个独立的计算单元,设此时两根斜拉索内力的水平分力分别为N1和N2,与桥塔的夹角分别为α1和α2,与主梁的夹角分别为β1和β2。应该注意,此时由于斜拉索的垂度和主梁的纵坡,斜拉索与桥塔、主梁的两个夹角并不互余;单根斜拉索两端的内力也不同,但单根斜拉索内力水平分量不变,因此,在斜拉索与桥塔、主梁的夹角确定后,两端点的反力也可随之确定。
|
| 图 3 斜拉体系分析简图 Fig. 3 Analysis diagram of cable-|stayed system |
力学分析简图如图 3所示,G1和G2分别为作用于斜拉索主梁锚固点处的主梁恒载(含二期恒载),Rt,R1,R2分别为A,B,C,3个约束处的约束反力,由3个约束处的平衡条件可得:
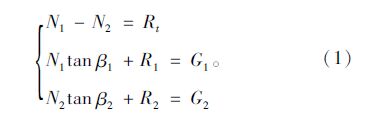
若可以调整两根斜拉索的N1和N2,使得3个约束处的约束反力均为零,那么在撤去约束后,结构将保持零位移状态。方程组(1)有N1和N2两个变量,却有3个约束条件,因此一般无法找到这样一组N1和N2。所以我们需要再引入一个变量F,该变量为作用在一侧约束点处的压重外力,假设该力作用于R1处,则上述平衡关系可以变为:
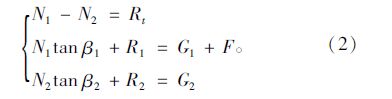
由式(2)可知,在任何情况下,都可以找到一组N1,N2,F满足上述方程组,使得删除斜拉索两端约束后的结构在约束方向位移为零。因此,该问题可以表述为确定锚固在桥塔同一点处的左右两根斜拉索的内力,使得桥塔锚固点的水平不平衡力以及一侧主梁锚固点的竖向不平衡力为零;同时,可以得到一外力F,使得另一侧主梁锚固点的竖向不平衡力也为零。即求解一目标水平索力Ntar和压重值Ftar,使得:
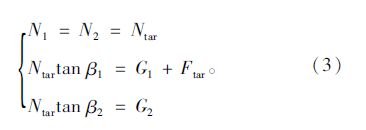
将该方法扩展到全桥结构上,约束斜拉段主梁竖向位移和桥塔纵向位移后,不断调整斜拉索内力,使锚固于桥塔同一点处的两侧斜拉索的内力水平分力相等,同时使其中某一侧斜拉索的主梁锚固点处的竖向支承反力也为零,这样,在撤去多余约束后,将另一侧的支承反力反向施加,即可得到桥塔纵向位移和主梁竖向位移均接近于零的成桥状态。该方法可视为同时考虑了塔、梁位移的零位移法。
如图 3所示,由于在斜拉索锚固处的桥塔纵向位移和主梁竖向位移均已经被约束,改变斜拉索内力或在约束方向施加外力并不会在主梁和桥塔内产生剪力,也不会对其他斜拉索内力产生影响(忽略塔梁的轴向压缩),因此,可将锚固在桥塔同一点处的一对斜拉索作为一个单独的调整单元,认为各调整单元之间相互独立。
基于以上分析,本文提出的协作桥合理成桥状态可通过以下计算步骤实现:
(1)将协作桥全桥模型拆分为悬索体系模型和斜拉体系模型两部分。对于悬索体系模型,采用文献[10]提出的分段悬链线法反复迭代确定其合理成桥状态。
(2)在协作桥成桥位置处建立有限元模型,悬索体系的主缆初始构形和缆、索初始内力按第(1)步计算结果输入,斜拉体系的内力可以任意赋给初始值。
(3)约束斜拉索锚固点处的桥塔纵向位移和主梁竖向位移,同时约束吊索锚点处的主梁竖向位移,做一次落架计算。
(4)计算完成后,提取任一斜拉体系调整单元内的3个约束点的约束反力Rt(0),R1(0),R1(0);斜拉索内力水平分量N1(0),N2(0);以及斜拉索分别与桥塔和主梁的夹角α1(0),α2(0),β1(0),β2(0)。
此时需要确定调整单元哪一侧是压重侧,即外力F施加于哪一侧主梁。设使主梁竖向约束反力R1为零的左侧斜拉索内力水平分量为NL,相应使主梁竖向约束反力R2为零的右侧斜拉索内力水平分量为NR,则由式(1)可得:
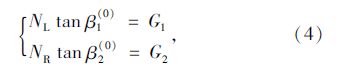
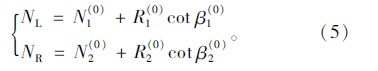
若NL>NR,则右侧主梁为压重侧,NL即所求目标水平索力Ntar;反之,则左侧主梁为压重侧,NR为所求目标水平索力Ntar,即应将使支座反力为零所需斜拉索水平内力较小的一侧作为压重侧,较大一侧的水平内力即为目标索力。
(5)选定压重侧之后,即可得到第一次迭代的斜拉索的目标水平内力Ntar(1)。如假设右侧主梁为压重侧,则有:
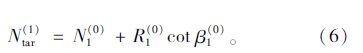
通过不断迭代将使斜拉索内力水平分量不断逼近目标值Ntar(1),但由于索力的变化,主梁和桥塔将产生新的轴向变位,斜拉索两端的相对几何关系及其与主梁、桥塔间的相对几何关系随之改变,因此该目标索力并不能使预期的约束反力变为零,还需进行外部迭代。
(6)当第(5)步计算收敛后,得到非压重侧的主梁约束反力R1(n-1)及斜拉索与主梁的交角β1(n-1),求得新的目标索力Ntar(n):
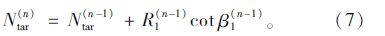
重新进行第(5)步迭代计算,直至预期的约束反力接近于零为止。随后,只需删除所有多余约束,并将主梁压重侧的约束反力反向施加作为压重Ftar,即可得到使主梁和桥塔位移为零的斜拉体系成桥状态。
(7)由于桥塔压缩以及主梁刚度的影响,悬索体系吊索传递的荷载与第(1)步计算主缆时的荷载已有所区别,悬索体系成桥状态需要更新,具体步骤如下:
① 根据第(5)步计算结果,提取吊索锚点处的主梁约束反力和桥塔塔顶压缩位移。
② 将吊索锚点处的主梁约束反力考虑吊索自重后作为新的主缆荷载,将桥塔压缩后的主缆矢高作为新的目标垂度,重新进行第(1)步计算,得到悬索体系合理成桥状态。
(8)删除协作桥全桥模型中的多余约束,带入第(6)步计算得到的斜拉体系初始内力和主梁压重,以及第(7)步计算得到的悬索体系主缆初始构形和缆、索初始内力,做一次落架计算,即可得到桥塔纵向位移和主梁竖向位移均接近于零的成桥状态。
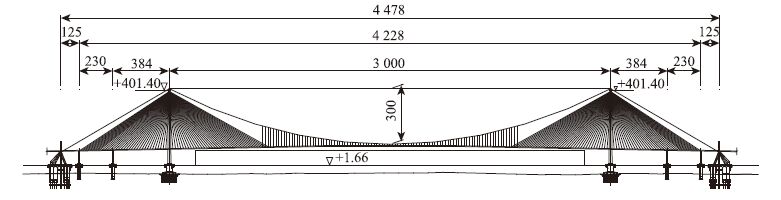
3 算例分析 3.1 算例简介在琼州海峡跨海通道工程可行性研究报告中,西线桥位主通航孔桥方案之一为主跨3 000 m的双塔斜拉-悬索协作桥,主桥跨径组成为(230+384+3 000+384+230) m,主跨由等效跨径1 344 m的斜拉体系与等效跨径1 656 m的悬索体系组合而成,吊跨比0.552。桥塔采用混凝土门式塔方案,主梁采用扁平流线型双箱分离式断面。全桥总体布置如图 4所示。
|
| 图 4 琼州海峡主跨3 000 m协作桥方案(单位:m) Fig. 4 Scheme of Qiongzhou Strait combined bridge with a main span of 3 000 m(unit:m) |
结构计算在通用有限元分析软件ANSYS上开展。缆索系统通过多段LINK10杆单元模拟,缆索初始内力通过降温或初应变施加;桥塔和主梁采用BEAM44梁单元模拟;主梁和缆索之间通过MPC184刚性杆单元连接,斜拉索同桥塔通过共用节点连接;塔梁之间连接装置通过COMBINE14弹簧单元模拟。
大跨径缆索承重桥梁是强非线性结构,其非线性效应主要有缆索垂度效应、梁柱效应、大位移效应等,为保证分析的精确性,需对以上非线性效应准确模拟。计算中斜拉索统一划分为20个节段以模拟缆索垂度效应,梁柱效应和大位移效应通过开启ANSYS中的大变形命令NLGEOM考虑。全桥有限元模型如图 5所示。

|
| 图 5 有限元模型 Fig. 5 Finite element model |
图 6给出了迭代法主要计算结果及其与直接组合法的比较情况。
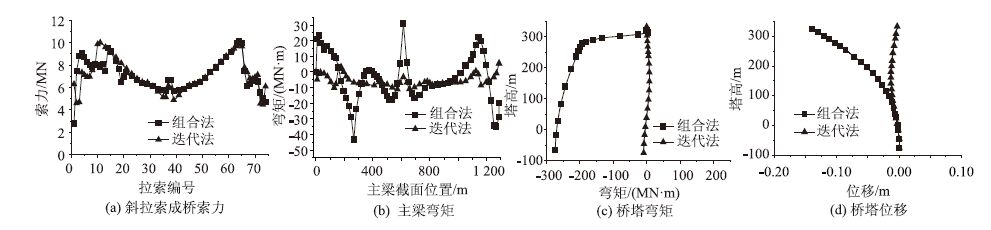
|
| 图 6 迭代法计算结果 Fig. 6 Calculation result of iterative method |
由图可见,对于斜拉索成桥索力,靠近桥塔的内侧20-30对斜拉索索力两者很接近,而中跨及边跨外侧索力则有明显差异,迭代法的边中跨斜拉索索力呈现明显对称性,组合法斜拉索索力变化无明显趋势;另外,迭代法的背索和端斜拉索索力大于组合法,背索索力的提高有助于增强活载作用下中跨的刚度。
对于主梁弯矩,迭代法结果明显小于组合法,特别是边跨和中跨外侧以及辅助墩处的主梁,迭代法最大约为10 MN·m,组合法最大约为48 MN·m。
对于桥塔弯矩,迭代法最大为8 MN·m,组合法最大为273 MN·m;对于桥塔纵向位移,迭代法最大为0.013 m,组合法最大为0.139 m;同组合法结果相比,迭代法的桥塔成桥弯矩和位移都很小,可以认为桥塔基本处于纯受压状态。
4 结论本文开展了斜拉-悬索协作桥合理成桥状态确定方法研究,主要结论如下:
(1)对于大跨径斜拉-悬索协作桥,如将斜拉段和悬索段作为独立的体系分别计算其成桥状态,再直接组合,将由于桥塔的P-Δ效应造成两大体系相互影响而无法得到理想的成桥状态。
(2)提出了一种确定协作桥合理成桥状态的迭代法,该方法以成桥时桥塔和主梁的位移最小为优化目标,通过迭代,不断调整斜拉体系主梁配重及斜拉索索力,使成桥时桥塔纵桥向不平衡力及主梁竖向不平衡力接近于零;同时不断更新悬索体系主缆构形和缆、索内力,使悬索体系主梁竖向位移接近于零。这样成桥时的桥塔将处于单纯受压状态,保持竖直,而主梁位于设计曲线上且内力处于刚性支承连续梁状态。
(3)以琼州海峡跨海通道的主跨3 000 m协作桥方案为例对上述方法进行了验证。结果表明,该方法计算结果整体优于直接组合法,有利于斜拉体系和悬索体系协同受力。
| [1] | GIMSING N J. Cable Supported Bridges-concept and Design [M].3rd ed. Chichester:John Wiley & Sons Ltd., 2012. |
| [2] | 王伯惠. 斜拉-悬索协作体系桥[J]. 辽宁省交通高等专科学校学报,2000,2(3):1-6. WANG Bo-hui. Combined Cable-stayed and Suspension Bridges[J]. Journal of Liaoning Provincial College of Communications,2000,2(3):1-6. |
| [3] | 王伯惠. 斜拉-悬索协作体系桥(续)[J]. 辽宁省交通高等专科学校学报,2000,2(4):1-7. WANG Bo-hui. Combined Cable-stayed and Suspension Bridges (Continued) [J]. Journal of Liaoning Provincial College of Communications,2000,2(4):1-7. |
| [4] | 张新军,张丹. 吊拉组合体系桥的研究进展[J]. 浙江工业大学学报,2007,35(5):553-558,585. ZHANG Xin-jun,ZHANG Dan. Research Progress on the Cable-stayed-suspension Hybrid Bridges[J]. Journal of Zhejiang University of Technology,2007,35(5):553-558,585. |
| [5] | 蒙云,刘东,孙淑红. 大跨度P-F-C吊拉组合桥设计研究[J]. 重庆交通学院学报,1999,18(4):8-12. MENG Yun,LIU Dong,SUN Shu-hong. P-F-C Large-span Combined Cable-stayed Suspension Bridge's Study in Design[J]. Journal of Chongqing Jiaotong Institute,1999,18(4):8-12. |
| [6] | 孙淑红,蒙云. 吊拉组合桥交接区域吊索的疲劳问题研究[J]. 重庆交通学院学报,1999,18(4):13-18. SUN Shu-hong,MENG Yun. The Boom's Fatigue in Joint Area of Combined Cable Stayed Suspension Bridge[J]. Journal of Chongqing Jiaotong Institute,1999,18(4):13-18. |
| [7] | 刘士林,王似舜. 斜拉桥设计[M]. 北京:人民交通出版社,2006. LIU Shi-lin,WANG Si-shun. Design of Cable-stayed Bridges[M]. Beijing:China Communications Press,2006. |
| [8] | 雷俊卿. 悬索桥设计[M]. 北京:人民交通出版社,2001. LEI Jun-qing. Design of Suspension Bridges[M]. Beijing:China Communications Press,2001. |
| [9] | 朱巍志,张哲,潘盛山,等. 自锚式斜拉-悬索协作体系桥合理成桥状态确定的分步算法[J]. 土木工程学报,2010,43(10):91-97. ZHU Wei-zhi,ZHANG Zhe,PAN Sheng-shan,et al. Stepwise Method of Calculation for the Rational Finished State of Self-anchored Cable-stayed Suspension Bridges[J]. China Civil Engineering Journal,2010,43(10):91-97. |
| [10] | 唐茂林,强士中,沈锐利. 悬索桥成桥主缆线形计算的分段悬链线法[J]. 铁道学报,2003,25(1):87-91. TANG Mao-lin,QIANG Shi-zhong,SHEN Rui-li. Segmental Catenary Method of Calculating the Cable Curve of Suspension Bridge[J]. Journal of the China Railway Society,2003,25(1):87-91. |
| [11] | 肖汝诚,项海帆. 斜拉桥索力优化及其工程应用[J]. 计算力学学报,1998,15(1):120-128. XIAO Ru-cheng,XIANG Hai-fan. Optimization Method of Cable Prestresses of Cable-stayed Bridges and Its Engineering Applications[J]. Chinese Journal of Computational Mechanics,1998,15(1):120-128. |
| [12] | 梁鹏,肖汝诚,张雪松. 斜拉桥索力优化实用方法[J]. 同济大学学报:自然科学版,2003,31(11):1270-1274. LIANG Peng,XIAO Ru-cheng,ZHANG Xue-song. Practical Method of Optimization of Cable Tensions for Cable-stayed Bridges[J]. Journal of Tongji University:Natural Science Edition,2003,31(11):1270-1274. |
 2015, Vol. 31
2015, Vol. 31
