扩展功能
文章信息
- 王苍和, 刘世忠, 贾一全
- WANG Cang-he, LIU Shi-zhong, JIA Yi-quan
- 刘家峡大桥钢管混凝土桥塔黏结滑移力学试验研究
- Mechanical Experimental Research of Bond-slip of CFST Pylon of Liujiaxia Bridge
- 公路交通科技, 2015, Vol. 31 (8): 89-92
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (8): 89-92
- 10.3969/j.issn.1002-0268.2015.08.015
-
文章历史
- 收稿日期: 2015-05-15
2. 兰州交通大学, 甘肃 兰州 730050
2. Lanzhou Jiaotong University, Lanzhou Gansu 730050, China
钢管混凝土由于具有承载能力高、塑性和韧性好、耐火和抗震性能好、制作与施工方便、经济效益好等优点[1],越来越多被采用于公路桥梁领域。刘家峡大桥为单跨地锚式悬索桥,主跨536 m,主梁采用钢桁式加劲梁,是国内同规模桥梁中最窄的悬索桥,宽跨比达到1∶44。其桥塔采用直径3 m、壁厚5 cm的钢管混凝土门式框架结构,钢管采用Q345D材质,管内灌注C40微膨胀混凝土,在塔顶设一道横梁。
由于悬索桥在施工过程中随着主缆架设、索夹和吊索安装、加劲梁与桥面板吊装以及主索鞍分阶段顶推,其桥塔顶部会产生不平衡力,在整个施工过程中,不同阶段桥塔受力方式与受力大小也不尽相同。鉴于桥塔在各施工阶段受力情况均有不同,钢管与混凝土相互作用效应复杂,且国内关于钢管混凝土结构黏结滑移力学性能研究较少[2],本文结合刘家峡大桥桥各施工阶段的受力特点,设计制作缩尺模型,将实际桥塔所受荷载换算为试验荷载进行加载,得到试验模型在试验荷载作用下钢管与混凝土共同工作时的力学性能,并结合有限元软件对其进行理论验证,合理分析桥塔内钢管与混凝土相互作用以及共同工作机理。
1 钢管混凝土工作机理钢管混凝土是“钢管套箍混凝土”(Steel Tube-Confined Concrete)的简称,是将混凝土灌入薄壁钢管内而形成的混合材料组合结构[3]。
混凝土强度、混凝土养护条件和龄期、界面长度、钢管内表面的粗燥程度、钢管的径厚比及构件长细比、混凝土的浇注方式、桥塔受力的偏心距等都会对钢管和混凝土之间的黏结作用有影响[4, 5, 6]。
引入文献[2]中,圆形截面钢管混凝土构件黏结强度计算公式:
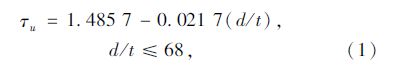
通过对“模型”的试验和研究,可以准确预测物理系统的相关性能,将这种可以被预测的物理系统称为“原型”[7]。
相似理论的理论基础有3个定理:几何相似、物理相似以及荷载相似。所谓的相似常数是指在一对相似现象中所具有的对应点在它的对应时刻上,同一物理量的值保持不变[8]。
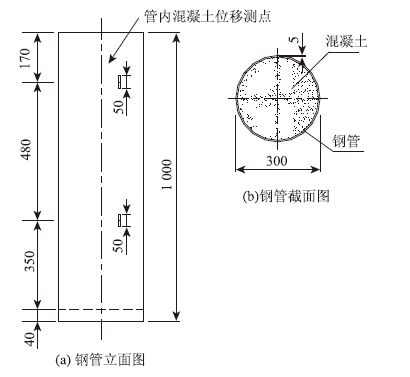
2.2 模型制作及试验过程刘家峡大桥钢管混凝土桥塔模型试验中,钢管及混凝土材料选用与原桥塔相同材料,即用Q345D钢材制作加工钢管,管内浇注C40微膨胀混凝土。为加载方便考虑,试验模型选用1/10的几何缩尺模型,即直径为300 mm,壁厚5 mm,高为1 000 mm的钢管混凝土试件。为研究分析钢管与混凝土共同工作时黏结滑移作用,对模型施加等效荷载,进行推出试验,并建立数值分析模型,获取实测数据加以分析。钢管混凝土推出试验模型如图 1所示。
|
| 图 1 推出试验钢管混凝土模型(单位:mm� Fig. 1 CFST model for push-|out test (unit:mm) |
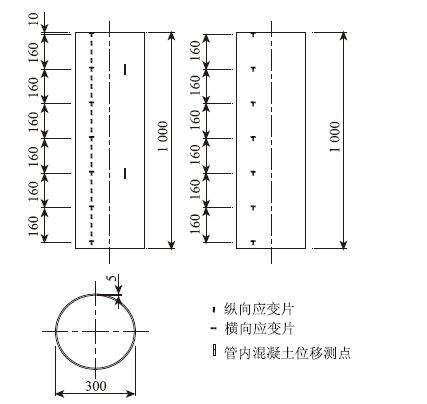
试验中,在钢管壁纵向布置电阻应变片,其间距为40 mm,环向也布置有电阻应变片,推出试验试件应变片及管内混凝土位移测点布置见图 2所示。测应变数据,根据钢管应力与黏结应力的微分成正比原理,可以得到钢管壁上纵向黏结应力的分布规律及大小,进而得到钢管的紧箍力沿桥塔纵向不同位置的分布规律,了解钢管混凝土所受轴压力与紧箍力之间的关系。为了更清楚、更直观地测试钢管与混凝土之间的相对滑动,在模型制作时,钢管壁开槽,插入短钢筋。试验中,通过测试短钢筋的位移来得到钢管内混凝土的滑移状况。
|
| 图 2 试件应变及位移测点布置示意图(单位:mm� Fig. 2 Schematic diagram of strain and displacement signal measuring points in specimen(unit:mm) |
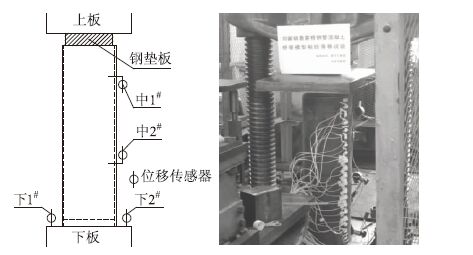
钢管一端的混凝土端面上放置一块比钢管内径略小的圆形钢垫板,在钢管另一端留有40 mm长一段未灌注混凝土的空钢管。试验时,试件一端钢管受压,另一端混凝土受压,钢管混凝土的结合面上会产生剪切力。试验按照40 kN一级进行加载,直到混凝土被推出30 mm,试验结束。试验加载装置及试件安装如图 3所示。当钢管中的混凝土被推出时,用位移计测量得到钢管与混凝土之间的相对滑移数值,由此可绘制得到滑移值和荷载值关系曲线。
|
| 图 3 试验装置 Fig. 3 Test equipment |
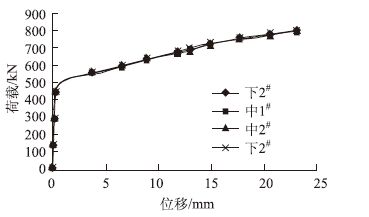
根据试验过程中所布置的位移测点和应变测点,对试验数据进行整理,不同荷载作用下,试验数据分析如表 1所示。混凝土推出的位移如图 4所示,分析荷载与位移曲线关系图,荷载位移曲线未出现峰值点和下降段,说明界面上的初始摩阻力大于钢管混凝土截面上的微观机械咬合力和胶结力所组合形成的最大黏结力。
| 初始滑移 荷载Ps/ kN |
黏结破坏 荷载Pu/ kN |
荷载比 Ps/Pu |
初始黏结 强度 τs/MPa |
极限黏结 强度τu/ MPa |
黏结破坏时 的滑移值 Su/mm |
| 320 | 536 | 0.60 | 0.35 | 0.59 | 1.98 |
|
| 图 4 试验荷载与位移关系图 Fig. 4 Load-displacement relationship from test |
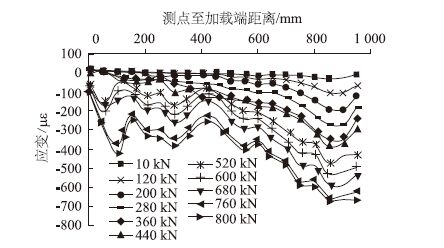
整理并分析数据,钢管混凝土桥塔推出试验荷载-应变关系曲线如图 5所示,其中横坐标为测点至加载端的距离,纵坐标为钢管壁上纵向应变值。由图 5可以看出,在整个试验过程中,钢管应变从受力端开始逐渐减小,当施加的荷载较小时,钢管应变随着测点到加载端距离的增大无明显变化。随着荷载的增加,钢管中部应变变大,此时钢管的应变随着测点到加载端的距离的增大也发生较大变化,主要由截面上残余的部分机械咬合力和摩擦力发挥作用。由于混凝土材料的不均匀性、钢管壁的粗糙程度等原因导致应变呈非线性变化[9],但总体呈逐渐增加趋势。在荷载加载端,依据变形协调条件,钢管的应变为最大值,加载端的黏结应力为零。
|
| 图 5 试验荷载-应变关系 Fig. 5 Load-strain relationship from test |
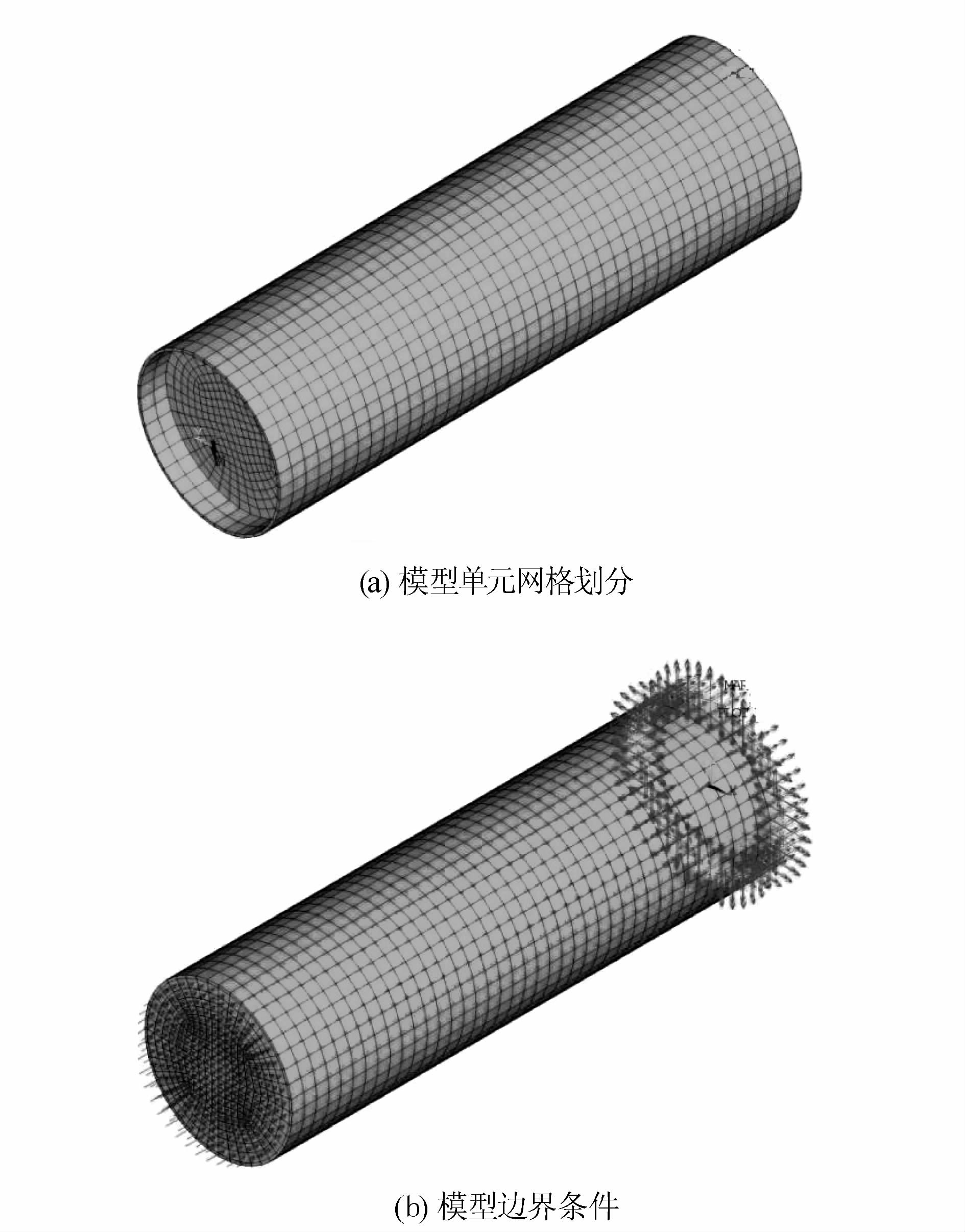
利用大型通用有限元分析软件ANSYS建立有限元模型进行分析,其中混凝土采用Solid65单元模拟,垫板和钢管采用Soud45单元模拟,有限元分析模型如图 6所示。采用有限元方法进行钢管混凝土受力分析时,可以得到构件中的局部应力的传递、不同材料界面的特性等问题的分析数据[10],分别反映出混凝土和钢材的非线性特性,并进一步模拟得到二者之间的界面黏结滑移数据[11]。
|
| 图 6 推出试验有限元模型 Fig. 6 Finite element model of push-|out test |
从有限元软件分析计算结果得出,混凝土推出过程中,内部混凝土受压应力最大值为13.2 MPa,外侧钢管受压应力最大值为28.2 MPa,均在材料的弹性变形范围内[12]。极限黏结强度与黏结破坏时滑移理论计算结果如表 2所示。
| 试件 长度 L/mm |
长细比 4L/D |
径厚比 D/t |
黏结破坏 荷载 Pu/kN |
极限黏结 强度 τu/MPa |
黏结破坏时的 滑移值Su/mm |
| 1 000 | 13.33 | 60 | 377.6 | 0.41 | 1.14 |
有限元模拟计算中钢管混凝土之间的极限黏结强度为0.41 MPa,黏结破坏时的滑移为1.14 mm。而实际的钢管混凝土桥塔模型推出试验中测得的极限黏结强度为0.59 MPa,黏结破坏时的滑移为1.98 mm,均大于非线性有限元计算结果。原因是由于钢管混凝土桥塔推出试验模型实际制作过程中混凝土材料的不均匀性以及钢管壁的粗糙程度,且ANSYS有限元分析中材料均为理想弹塑性模型,没有考虑这些因素,因此导致实际黏结破坏荷载较有限元模拟的偏大。
4 结论本文以刘家峡悬索桥钢管混凝土桥塔为原型制作几何缩尺模型并模拟桥塔实际受力换算试验荷载对模型进行加载,通过对试验数据进行分析,充分地验证了在荷载逐级加载作用下,钢管和混凝土共同工作时的几个阶段:初始阶段,钢管与混凝土无明显相对滑移,两者可以共同受力;随荷载的增加,试件两端在局部范围内混凝土与钢管之间开始产生微小的相对滑动,该范围的胶结力被破坏;随着荷载的进一步增大,试件两端的相对滑移继续增大,并开始逐渐向构件中部发展,这时胶结力只存在于还没产生相对滑移的部位上,荷载位移变化曲线呈线性关系。
将试验数据与有限元分析结果进行对比,发现有限元分析所得钢管与混凝土之间的极限黏结强度及黏结破坏时的滑移位移均小于试验模型中的实测数据,说明采用有限元方法计算的结果能够得到对于工程偏安全的结果,对于钢管混凝土结构整体复杂受力分析可采用试验测试结果建立黏结-滑移本构关系进行精确模拟。
| [1] | 赵鸿铁.钢与混凝土组合结构[M].北京:科学出版社,2001. ZHAO Hong-tie. Steel & Concrete Composite Structure[M]. Beijing: Science Press, 2001. |
| [2] | 杨勇.型钢混凝土粘结滑移基本理论及应用研究[D].西安:西安建筑科技大学,2003. YANG Yong. Study on Basic Theory and Its Application of Bond-slip between Shaped Steel and Concrete [D]. Xi'an: Xi'an University of Architecture & Technology,2003. |
| [3] | 杨勇,赵鸿铁,王彦宏.型钢混凝土保护层弹塑性屈曲分析[J]. 西安建筑科技大学学报:自然科学版,2001,33(3):207-211. YANG Yong, ZHAO Hong-tie, WANG Yan-hong. Elastoplastic Bulking Analysis of Concrete Cover for SRC Beams and Columns[J]. Journal of Xi'an University of Architecture & Technology: Natural Science Edition, 2001,33(3):207-211. |
| [4] | 蔡绍怀.我国钢管混凝土结构技术的最新进展[J].土木工程学报,1999,32(4):16-26. CAI Shao-huai. Recent Development of Steel Tube-confined Concrete Structures in China [J].China Civil Engineering Journal, 1999,32(4):16-26. |
| [5] | 康希良, 程耀芳, 张丽,等. 钢管混凝土粘结-滑移本构关系理论分析[J]. 工程力学, 2009 (10):74-78. KANG Xi-liang, CHENG Yao-fang, ZHANG Li,et al. Theoretical Analysis of Bond-slip Constitutive Relationship for CFST [J]. Engineering Mechanics,2009 (10):74-78. |
| [6] | 韩林海.钢管混凝土结构的理论与实践[C]//第十届全国结构工程学术会议论文集:第I卷. 北京:《工程力学》杂志社,2001:226-251. HAN Lin-hai. The Theory and Practice of CFST Structure(Volume I)[C]// Proceeding of 10th National Conference on Structure Engineering. Beijing:Engineering Mechanics Press,2001:226-251. |
| [7] | 聂建国,柏宇,李盛勇,等. 钢管混凝土核心柱轴压组合性能分析[J]. 土木工程学报,2005,38(9): 9-13. NIE Jian-guo,BAI Yu,LI Sheng-yong,et al. Analyses on Composite Column with Inside Concrete Filled Steel Tube under Axial Compression[J]. China Civil Engineering Journal,2005,38 (9): 9-13. |
| [8] | 康洪震,钱稼茹. 钢管混凝土叠合柱轴压强度试验研究[J]. 建筑结构,2006,36 (增1): 22-25. KANG Hong-zhen,QIAN Jia-ru. An Experiment Study of Axial Compressive Strength of Concrete Filled Steel Tube Composite Columns[J]. Building Structure,2006,36(S1): 22-25. |
| [9] | 李鹏. 钢管高强混凝土核心柱受压性能试验与理论研究[D]. 杭州: 浙江大学,2005: 29-49. LI Peng. Experimental and Theoretic Study on Compression Characteristics of Composite Column with Core of High-strength CFST[D]. Hangzhou: Zhejiang University,2005: 29-49. |
| [10] | GB 50010—2002,混凝土结构设计规范[S]. GB 50010—2002,Code for Design of Concrete Structures[S]. |
| [11] | 韩林海,冯九斌.混凝土的本构关系模型及其在钢管混凝土数值分析中的应用[J]. 哈尔滨建筑大学学报,1995,28(5): 26-32. HAN Lin-hai,FENG Jiu-bin. Constitutive Relations of Concrete and Its Application in the Integral Analysis of Concrete Filled Steel Tube[J]. Journal of Harbin University of Architecture and Engineering,1995, 28 (5): 26-32. |
| [12] | CECS 188: 2005,钢管混凝土叠合柱结构技术规程[S]. CECS 188:2005, Technical Specification for Steel Tube-reinforced Concrete Column Structure[S]. |
 2015, Vol. 31
2015, Vol. 31
