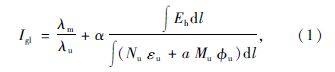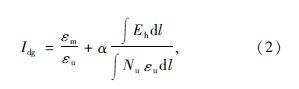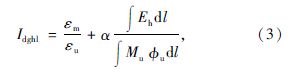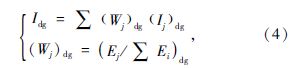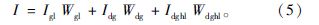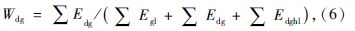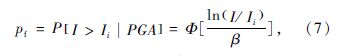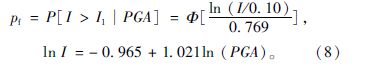扩展功能
文章信息
- 刘震
- LIU Zhen
- 中承式钢管混凝土拱桥地震易损性分析
- Analysis on Seismic Fragility of Half-through CFST Arch Bridge
- 公路交通科技, 2015, Vol. 31 (8): 72-79
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (8): 72-79
- 10.3969/j.issn.1002-0268.2015.08.013
-
文章历史
- 收稿日期: 2014-07-25
桥梁是交通线中的枢纽结构,在地震过程中一旦受到破坏将严重影响交通线功能的实现,并对之后的救灾工作造成巨大困难。过去发生的一些地震,如1976年唐山地震、1971年San Fernando地震、1994年Northridge地震、1995年Kobe地震、1999年Chi-Chi地震和2008年汶川地震,都表明桥梁是公路中极易损坏的结构。
桥梁地震易损性分析可以得到特定类型桥梁在特定地震作用下的损伤概率,这对于我国公路网的建设、灾害评估、地震加固和灾后应急响应决策等有指导意义。在国外桥梁易损性研究已经成为桥梁抗震的一个重要方面:Hwang[1]对美国中东部高速公路连续梁桥进行易损性分析,并给出了受New Madrid地震带影响的此类桥梁易损性曲线。Pan[2]分析纽约州高速公路连续钢梁桥,建立了与震级和震源距离相关的易损性曲面。Agrawal[3]对美国纽约州有抗震措施的连续钢梁桥进行分析模拟,得出了有抗震措施的连续梁桥地震易损性曲线。Tavares[4]就魁北克市55号高速公路上的Chemin des Dalles桥进行易损性分析,得出综合破坏概率。
在我国中承式钢管混凝土拱桥以其独特的受力和外形优点,在近20 a以极高速度持续增长,在交通线中承担着重要任务,新的拱桥桥型也层出不穷[5, 6],而我国现阶段对此类桥梁的地震易损性分析研究较少。为此,本文将以我国常见的中承式钢管混凝土拱桥作为研究对象,考虑其最易发生破坏的拱肋、吊杆、横梁部位的损伤,对拱桥系统进行地震易损性分析。
1 地震易损性分析的基本步骤(1)结合国内工程实际和统计数据确定对桥梁结构抗震敏感的不确定因素取值范围。
(2)结合地质条件选取一系列地震加速度时程,并通过对峰值加速度进行调幅处理使其满足易损性分析需要。
(3)量化用于模拟桥梁结构自身参数不确定性,并确定其分布概率。
(4)使用超拉丁抽样方法组成桥梁样本并与地震数据配对,从而建立一系列的桥梁-地震样本。
(5)每一个桥梁-地震样本通过数值模拟分析出桥梁结构响应。
(6)根据钢管混凝土拱桥受力和破坏特性使用基于变形或内力和积累耗能的双重破坏准则判断其破坏状态。
(7)回归地震峰值加速度与不同破坏状态概率的关系,形成易损曲线。
(8)回归地震震级和震源距离与不同破坏状态概率的关系,形成易损曲面。
2 桥梁模型及其构件力学特性的不确定性因素在实际工程中结构参数、材料性能、施工方法、荷载效应等因素都存在着一定程度上的不确定性,针对不同工程不确定性因素对地震抗力的敏感程度也各不相同。本文中的桥梁结构模型将根据国内工程实际和统计数据从结构参数、材料性能与荷载效应3个方面考虑桥梁结构的不确定性,力求桥梁样本贴近工程实际。
2.1 桥型选择2000年后钢管混凝土拱桥成为国内修建的主要拱桥桥型,其中超过50 m跨径的中承式拱桥截止2010年共有93座(占到了29.2%)[7]。故本文采用中承式钢管混凝土拱桥作为研究对象是较有代表性的,同时也可以为拱桥的建设提供有益的参考。
2.2 跨径选择对已经建成的钢管混凝土拱桥进行分析,其主要应用跨径在200 m以内,超过300 m跨径钢管混凝土拱桥极少,截止2010年仅有9座[7]。由于跨径小于90 m的拱桥,在钢筋混凝土拱桥标准图范围内,目前多采用钢筋混凝土拱桥,且跨度小于90 m的钢管混凝土拱桥大多为外部静定的系杆拱桥,与本文研究对象差异较大。本文将跨径范围确定为90~200 m,并根据陈宝春教授的统计资料[8],将跨径的概率分布确定为均匀分布。
2.3 桥面宽度桥面宽度根据文献[9]中的钢管混凝土拱桥常用桥宽并根据国内的工程实际在20~30 m进行取值。
2.4 拱肋参数根据2009年对131座钢管混凝土统计分析,有接近一半的拱肋截面选用了哑铃形,其中43座竖向哑铃形,24座横向哑铃形。工程上哑铃形钢管混凝土拱桥一般常用的矢跨比范围为1/4~1/5.5,其中有大约60%采用了1/5的矢跨比 [10]。故本文将样本桥梁的拱肋截面确定为哑铃形,矢跨比根据文献[8]中的比例确定。
拱轴线方面,悬链线采用较多,达到65%,为了使恒载压力线与拱轴线尽量相适应,以减少拱肋所承受的弯矩,同时让拱肋具有较好强度和稳定性,需要确定一个合理的拱轴系数。根据文献[10]中盛叶对哑铃形钢管混凝土拱桥的分析,发现实际工程上常选用1.1~1.6作为拱轴系数,拱轴系数与跨径之间并没有明显的相关关系。故将桥梁样本拱轴线线型确定为悬链线,并将拱轴系数取在1.1~1.6之间,按均匀分布取值。
钢管直径和截面高度方面,实际工程上一般的取用范围分别为450~1 500 mm和1.2~3.75 m,且和跨径有一定的相关关系,在文中对桥梁样本确定时按照文献[10]中统计数据回归出的跨径与钢管直径和钢管高度公式取值。
含钢率ρ%=As/Ac,式中As为拱肋截面钢材面积,Ac为拱肋截面混凝土面积。《钢管混凝土规程》(DL/T508—1999) [11] 中规定钢管混凝土的含钢率应在4%~20%,工程上通常取值为4%~12%,且有随着跨径的增大而减小的趋势。本文通过盛叶统计数据回归出跨径与含钢率的经验公式和工程实践取值,并通过含钢率和钢管直径确定拱肋钢管的厚度。
2.5 横撑与吊杆数量根据文献[7]对327座钢管混凝土拱桥统计分析发现:随着宽跨比减少横撑数目逐渐增加,绝大部分无横撑拱桥都为宽桥。横撑对拱桥横向地震响应影响较大,目前工程上主要采用的横撑有一字形横撑、K形横撑、X形横撑,本文根据桥梁跨径对横撑形式进行选取。吊杆方面,跨径小于100 m时,吊杆间距一般在4~6 m之间;当跨径在100~200 m之间时,吊杆间距一般为5~8 m。本文基于这些统计规律按照样本拱桥的跨径和净宽对横撑和吊杆数量进行取值。
2.6 桥面系拱桥桥面系形式按桥面板布置可以分为纵铺式、横铺式和整体式,2005年以前多以纵铺式为主;2005年以后新建拱桥桥面布置形式多以整体式为主,且数量占到了接近一半。 68%的拱桥加设了纵向加劲梁,以提高桥面整体刚度和稳定性[7],故桥梁样本桥面布置形式为整体式,且桥面中除了设置横梁外还根据工程实践设置了两道纵向加劲梁。
2.7 材料参数材料方面,Q345钢和C50混凝土成为2005以后新建钢管混凝土拱桥拱肋材料的主流,Q345钢的使用率达到了93.5%,C50混凝土的使用率达到了74.4%[7],故将样本混凝土拱肋材料选为Q345钢和C50混凝土。根据Pan研究成果[12]和国内钢管混凝土拱桥施工特点将所使用材料参数的不确定性参数及其分布总结于表 1。
| 模型参数 | 分布类型 | 均值/MPa | 变异量/MPa |
| C50混凝土最大压应力 | 正态分布 | 54.92 | 3.00 |
| Q345钢屈服应力 | 正态分布 | 378.95 | 20.70 |
根据《公路桥涵设计通用规范》(JTG D60—2004) [13]和国内工程实际确定恒载,不考虑桥梁活载。
2.9 桥梁样本在确定对地震损伤较为敏感的几个参数的概率分布以后,使用超拉丁法进行抽样,根据跨径进行分组抽样,而后确定与跨径有相关关系的参数,最后确定与跨径无明显相关关系的参数。本文抽取了15组桥梁参数,得到了10个桥梁样本见表 2。
| 样本号 | 桥长/m | 拱轴线 系数 |
桥宽/m | 横撑 数量 |
吊杆 间距/m |
拱肋直径/ mm |
| 1 | 200 | 1.109 | 25 | 7 | 8 | 1200 |
| 2 | 188 | 1.489 | 28 | 5 | 5 | 1250 |
| 3 | 175 | 1.277 | 28 | 5 | 7 | 1120 |
| 4 | 168 | 1.247 | 30 | 6 | 6 | 1100 |
| 5 | 155 | 1.274 | 32 | 5 | 5 | 1070 |
| 6 | 144 | 1.295 | 30 | 4 | 6 | 980 |
| 7 | 126 | 1.484 | 26 | 5 | 7 | 1010 |
| 8 | 105 | 1.305 | 20 | 5 | 5 | 800 |
| 9 | 94 | 1.372 | 24 | 3 | 3 | 600 |
| 10 | 90 | 1.386 | 20 | 4 | 4 | 500 |
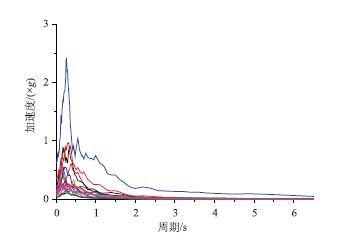
根据中国地震动反应谱特征周期区划图[14],并结合我国拱桥桥位一般的地质条件,从太平洋地震工程研究中心选取震级在5.5~8.0级,震源深度40 km 以内,震源距离在40 km以内,特征周期在3.5~4.5 s,剪切波速在300~700 m/s的地震动记录15条,见图 1。地震动水平峰值加速度覆盖范围为0.05g~0.70g,竖向峰值加速度覆盖范围为0.02g ~0.50g。为保证地震记录的真实性和准确性,提取地震动记录的水平两向地震波和竖向波作为一个地震样本,这些样本基本可以保证《公路桥梁抗震设计规范》(JTJ 004—2005)[15]中对多遇地震PGA的要求。为了使地震动强度的覆盖范围更广,对这15条地震原始记录进行调幅处理,以满足规范中对罕遇地震的要求。原始地震记录和经调幅处理后的地震波数据共30条,其水平峰值加速度覆盖范围为0.05g~0.14g,竖向峰值加速度覆盖范围为0.02g~1.00g。
|
| 图 1 未调幅地震动反应谱特征 Fig. 1 Response spectra of unscaled earthquake records |
|
|
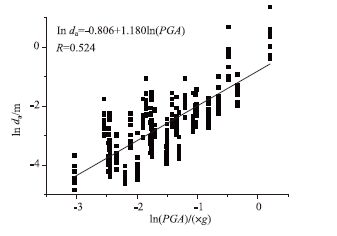
针对上文基于桥梁结构不确定性建立的10组桥梁样本与30组地震动样本进行配对,分别使用数值方法进行模拟,并记录下拱桥关键构件的最大动力响应,具体包括拱顶位移da、1/4拱肋位移db、拱顶弯矩Ma、1/4拱肋弯矩Mb、拱脚弯矩Mc、拱顶轴力Fa、1/4拱肋轴力Fb、拱脚轴力Fc、吊杆位移dd、吊杆轴力Fd、横梁弯矩Me共计11个动力响应指标。将记录的最大地震动响应分别与对应的水平PGA和竖向PGA在对数空间中绘制出来,根据Cornell等对地震需求和地震动参数-地震动PGA的研究发现,两者服从对数正态分布[16],图 2、图 3给出通过对数回归得到的拱顶位移、拱顶弯矩分别和水平PGA的拟合结果。
|
| 图 2 拱顶总位移与水平PGA回归关系 Fig. 2 Regression relation between displacement on arch top and horizontal PGA |
|
|
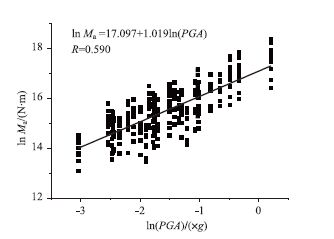
|
| 图 3 拱肋最大弯矩与水平PGA回归关系 Fig. 3 Regression relation between maximum bending moment on arch top and horizontal PGA |
|
|
桥梁损伤指标是评估在外力作用下桥梁结构受到破坏的无量纲指标,在分析桥梁破坏时通过对桥梁损伤指标进行划分,进而对桥梁结构破坏进行分级。《地震灾害评估》[17]中给出了按桥梁承重构件破坏程度和交通能力丧失程度划分破坏等级标准,桥梁破坏共划分为基本完好、轻微破坏、中等破坏、严重破坏以及毁坏5个等级。在《地震现场工作:第三部分调查规范》(GB /T18208.3—2000) [18]附录中,给出拱桥破坏等级划分标准并首次考虑非承重构件的影响,也是将桥梁破坏划分为基本完好、轻微破坏、中等破坏、严重破坏以及毁坏5个破坏等级,针对拱桥每个破坏等级的宏观评价描述如表 3所示。拱腹微裂缝、拱身微裂等破坏描述只是对拱桥承载能力进行定性的评价,没有定量关系对具体拱桥结构的损伤评定造成了困难。针对这一困难谢开仲教授[19]根据钢管混凝土拱桥的受力特点和破坏模式提出了基于变形或内力和积累耗能的双重破坏准则,这一准则对钢管混凝土拱桥的抗震能力进行了定量的分析。故本文综合上述评价标准并结合谢开仲教授的双重破坏准则对桥梁样本进行损伤评定。
| 损伤状态 | 损伤描述 | ||
| 承重结构 | 非承重结构 | 宏观表现 | |
| 基本完好 | 完好 | 基本完好 | |
| 轻微破坏 | 只出现允许的裂缝, 承载力无明显影响 |
有损坏 | 拱腹有微裂缝,拱 身微裂 |
| 中等破坏 | 遭受损伤或局部 损坏 |
附属结构 破坏较重 |
拱上结构出现较大 裂缝,拱圈部位出 现小裂缝 |
| 严重破坏 | 主要承重结构严重 破坏 |
- | 拱圈严重开裂,拱 轴线明显变形 |
| 毁坏 | 结构不能使用 | - | 拱倒,落拱 |
基于变形或内力和积累耗能的双重破坏准则,根据地震力作用下,拱桥各构件产生的内力或变形和累积耗能与承受能力的关系,对结构整体进行破坏程度评定。
谢开仲教授双重破坏准则中[19],对钢管混凝土拱桥的各构件破坏指数计算公式如下:
拱肋
吊杆 吊杆横梁 式中,Igl,Idg,Idghl分别为拱肋、吊杆和吊杆横梁的破坏指数;λm,λu分别为地震力作用下拱肋截面最大压弯系数和拱肋极限压弯系数;εm,εu分别为地震力作用下构件产生的最大应变和构件极限应变;φu为构件极限状态对应的曲率;Eh为地震力作用下截面积累的能量;Nu为构件的极限轴力;Mu为构件的极限弯矩;l为构件的长度;α为系数,根据文献[19]的建议α取0.139。地震力对桥梁结构中同类构件产生的破坏程度不同,根据各个构件在地震力作用下积累能量的大小来评定该构件对此类构件破坏指数贡献程度,其中破坏指数的贡献程度用权重系数W来表示,例如吊杆整体破坏指数为:
式中,(Wj)dg为第j根吊杆构件破坏指数的权重;(Ij)dg为第j根吊杆构件的破坏指数;Ej为第j根吊杆构件在地震力作用下所积累的能量;∑Ei为吊杆整体在地震力作用下所积累的总能量。根据相同原则可以计算拱桥整体的破坏指数为:
桥梁结构中一类构件整体权重计算,以吊杆为例:
式中,Igl,Idg,Idghl分别为拱肋、吊杆、吊杆横梁的整体破坏指数;Wgl,Wdg,Wdghl分别为拱肋、吊杆、吊杆横梁整体破坏指数在整桥破坏指数中的权重;∑Egl,∑Edg,∑Edghl分别为拱肋、吊杆、吊杆横梁整体在地震力作用下所积累的总能量。 5.3 地震破坏评定在地震力的作用下桥梁结构会产生相应的响应,根据响应程度不同对桥梁进行结构地震破坏评估。具体到双重破坏准则,由于破坏准则中的破坏指数表征了变形、内力和能量积累与结构所能承受极限的关系,故地震作用对桥梁结构破坏程度的评估可以用破坏指数取值范围进行判断。根据《公路桥梁抗震细则》(JTG/T B02—01—2008) [20]规定和文献[19]中的建议,将不同破坏程度的桥梁破坏指数范围定义于表 4。
| 破坏程度 | 基本完好 | 轻微破坏 | 中等破坏 | 严重破坏 |
| 破坏指数范围 | 0.00~0.10 | 0.10~0.30 | 0.30~0.50 | 0.50~0.70 |
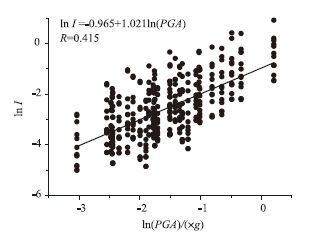
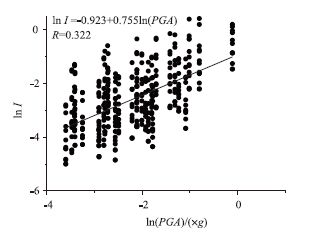
针对本文使用10组桥梁样本与30组地震动样本配对形成的300组桥梁-地震样本分别进行数值模拟得到桥梁响应,使用双重破坏准则得到桥梁的破坏指数,并对破坏指数与PGA进行对数回归,见图 4、图 5。
|
| 图 4 破坏指数与水平PGA回归关系 Fig. 4 Regression relation between damage index and horizontal PGA |
|
|
|
| 图 5 破坏指数与竖向PGA回归分析 Fig. 5 Regression relation between damage index and vertical PGA |
|
|
桥梁易损性曲线为在给定的PGA作用下,桥梁结构达到或者超越某种损伤状态的条件概率。具体到样本评定使用的双重破坏准则,是在一定的PGA条件下,桥梁结构破坏指数超过某一损伤状态其取值范围下限的概率。基于上述破坏指数与PGA的对数回归公式,分析不同PGA下桥梁破坏指数的取值,并根据桥梁易损性的定义可以得到在一定PGA条件下桥梁某一损伤的条件概率:
式中,pf为桥梁结构的失效概率;Ii为某一损伤状态下,桥梁破坏指数的取值范围的下限值,i=1,2,3,4,分别为轻微破坏、中等破坏、严重破坏、倒塌;β为破坏指数与PGA对数回归的对数标准差,以水平PGA为自变量时为0.769,以竖向PGA为自变量时为0.890。以水平PGA为自变量,使桥梁结构达到轻微破坏概率为:
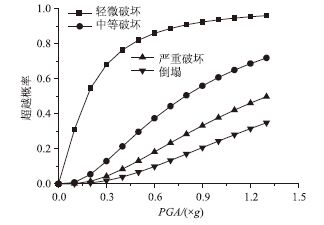
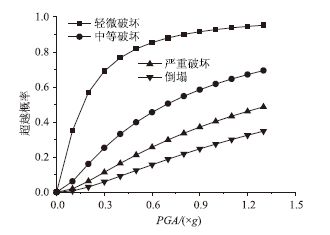
根据上述公式可以得到拱桥整体结构在不同损伤状态的超越概率如图 6、图 7所示。
|
| 图 6 基于水平峰值加速度的易损性曲线 Fig. 6 Fragility curves based on horizontal PGA |
|
|
|
| 图 7 基于竖向峰值加速度的易损性曲线 Fig. 7 Fragility curves based on vertical PGA |
|
|
通过水平和竖向PGA的桥梁易损性曲线对比可以发现,竖向PGA较大的地震样本比水平PGA较大的地震样本对桥梁结构产生的可能损伤更大,例如含有PGA为0.5g竖向地震波的地震样本对结构造成轻微破坏、中等破坏、严重破坏和倒塌的概率分别为82%,40%,21%和12%,而相同的损伤程度需要含有PGA为0.7g水平地震波的地震样本才能达到,这说明拱桥结构对竖向地震波的损伤更加敏感。水平和竖向PGA与破坏指数回归的对数标准差分别为0.769和 0.890,说明地震样本的竖向地震波对拱桥结构产生损伤的离散度更大。基于以上两点可以得出:地震中竖向地震波对拱桥结构产生损伤较大且损伤的随机性更为显著。
使拱桥样本产生轻微破坏和中等破坏的水平和竖向PGA中值分别为0.3g和0.2g与0.8g和0.7g,而拱桥结构产生倒塌的水平和竖向PGA中值已经超越地震样本的PGA覆盖范围,故认为可以达到《公路桥梁抗震设计规范》(JTJ004—2005)[15] 中的在多遇地震下不受损坏或不需修理,在罕遇地震下不致倒塌或严重损伤的要求。
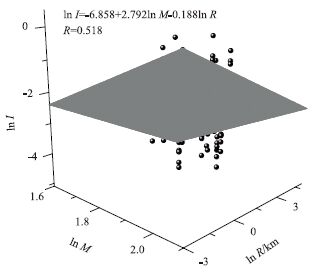
6.3 桥梁样本易损曲面相对于地震动的水平和竖向PGA记录,地震震级和震源距离的记录更能准确反映地震动的特性,研究桥梁易损性与震级和震源距离的相关性更具有实际意义。本文选取地震动数据中15组未经过调幅处理的原始地震动记录与10组桥梁数据组成150组桥梁-地震样本,并根据PAN[21]的建议回归公式,将这150组基于原始地震记录样本的破坏指数与震级和震源距离进行对数回归分析,见图 8。
|
| 图 8 破坏指数与震级和震源距离回归关系 Fig. 8 Regression relation of damage index with earthquake magnitude and epicenter distance |
|
|
ln(Sd/Sc)=a+bln M+cln R,
式中,Sd/Sc为地震需求与桥梁能力的比,对应于本文为使用双重破坏准则的破坏指数I;M为地震动震级;R为震源距离。
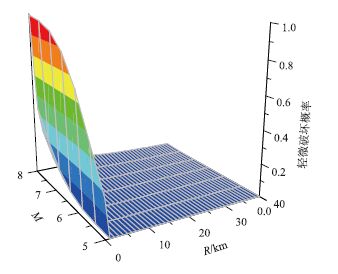
通过与上文桥梁易损曲线相似的概率分析,可以得到震级震源距离与4种桥梁破坏状态间的概率关系即桥梁易损关于震级和震源距离的曲面,如图 9~图 12所示。
|
| 图 9 轻微破坏易损性曲面 Fig. 9 Fragility surface of slight damage |
|
|
|
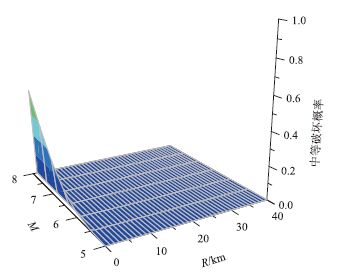
| 图 10 中等破坏易损性曲面 Fig. 10 Fragility surface of moderate damage |
|
|
|
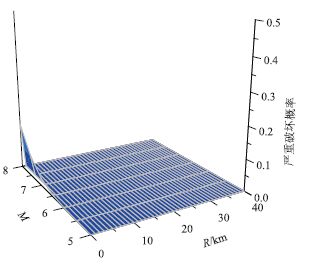
| 图 11 严重破坏易损性曲面 Fig. 11 Fragility surface of serious damage |
|
|
|
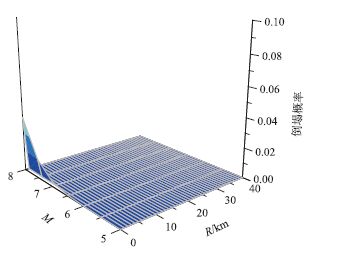
| 图 12 倒塌易损性曲面 Fig. 12 Fragility surface of collapse |
|
|
由于R=0会使方程产生发散,故使用一个较小值代替R=0计算破坏概率,且较小值计带入回归方程算出的破坏指数要与样本中R=0的地震样本使桥梁产生破坏指数的均值相同,经过试算发现使用R=0.01代替R=0这一点较为适合。
通过易损曲面可以发现震源距离要比震级对结构损伤影响更大,由于近源地震含有能量较大的竖向地震波,这也验证了竖向地震波会对拱桥结构带来更大的损伤。当R>10的非近缘小于8级地震只会对6%的桥梁产生轻微破坏,基本不会产生中等程度以上的破坏。严重破坏只在震源距离小于1 km震级大于8级时才有低于10%的概率发生,满足《公路桥梁抗震设计规范》(JTJ004—2005)[15]中对此类桥梁的要求。
7 结论本文对国内广泛使用的中承式钢管混凝土拱桥进行了地震易损性分析,拱桥模型参数取值均基于国内的工程实际和统计分析数据,地震记录充分考虑中国地质情况,得出的桥梁易损性曲线和曲面可用于国内工程实际。通过研究主要得出以下结论:
(1)本文中基于钢管混凝土拱桥地震力作用下的受力特点及破坏模式进行了拱桥易损性分析,为今后桥梁易损性分析提供了有益的参考。
(2)依据桥梁易损性曲线可知,普遍使用的地震动强度指标PGA与桥梁破坏指数在对数空间下拟合并不理想,水平和竖向PGA与破坏指数相关性系数分别为0.415 和0.322,而破坏指数与震级和震源距离在三维对数空间下拟合相对较好,相关系数为0.518。因此震级和震源距离比PGA更能评估地震对桥梁可能的损伤。
(3)根据本文得出的易损性曲线可知,使拱桥结构达到轻微破坏、中等破坏和严重破坏的水平PGA为别为0.3g,0.9g,1.3g,表明在《公路桥梁抗震设计规范》(JTG004—2005)[13]中的8度烈度(加速度为0.3g)下基本不产生损伤,而在罕遇地震作用下基本控制在中等程度的破坏。
(4)根据本文得出桥梁结构基于震级和震源距离的易损曲面分析可知,近源地震对桥梁破坏较为严重,而非近源地震对桥梁破坏相对较轻。当R>10 km发生小于8级的地震桥梁94%的概率处于基本完好状态。由于缺少符合国内地质条件的地震数据特别是强震记录,所以易损曲面缺少对罕遇地震分析,这需要今后展开进一步的研究。
| [1] | HWANG H, 刘晶波. 地震作用下钢筋混凝土桥梁结构易损性分析[J]. 土木工程学报, 2004,37(6): 47-51. HWANG H, LIU Jing-bo. Seismic Fragility Analysis of Reinforced Concrete Bridges[J]. China Civil Engineering Journal, 2004,37 (6): 47-51. |
| [2] | PAN Y, AGRAWAL A K, GHOSN M. Seismic Fragility of Continuous Steel Highway Bridges in New York State[J]. |
| [3] | AGRAWAL A K, GHOSN M, AlAMPALLI S, et al. Seismic Fragility of Retrofitted Multispan Continuous Steel Bridge in New York[J]. |
| [4] | TAVARES D H, SUESCUN J R, PAULTRE P, et al. Seismic Fragility of a Highway Bridge in Quebec[J]. |
| [5] | 霍学晋, 许圣祥, 韩立中. 蝶形拱桥主梁的非线性行为及影响因素分析[J]. 公路交通科技, 2014,31(5): 57-65. HUO Xue-jin, XU Sheng-xiang, HAN Li-zhong. Analysis on Nonlinearity Behavior of Main Beam of Butterfly-shaped Arch Bridge and Its Influencing Factors[J]. Journal of Highway and Transportation Research and Development,2014,31(5): 57-65. |
| [6] | 霍学晋, 韩立中. 蝶形拱桥的非线性行为分析[J]. 公路交通科技, 2013,30(9): 53-60. HUO Xue-jin, HAN Li-zhong. Analysis on Nonlinear Behavior of Butterfly-shaped Arch Bridge[J]. Journal of Highway and Transportation Research and Development,2013,30(9):53-60. |
| [7] | 陈宝春, 刘福忠, 韦建刚. 327座钢管混凝土拱桥的统计分析[J]. 中外公路, 2011(6): 96-103. CHEN BAO-chun, LIU FU-zhong, WEI Jian-gang. Statistical Analysis of 327 Concrete-filled Steel Tubular Arch Bridges[J]. Journal of China & Foreign Highway,2011 (6): 96-103. |
| [8] | 陈宝春, 陈康明, 赵秋. 中国钢拱桥发展现状调查与分析 [J].中外公路,2011(2): 121-127. CHEN Bao-chun, CHEN Kang-ming, ZHAO Qiu. Investigation and Analysis of Steel Arch Bridges in China[J]. Journal of China & Foreign Highway, 2011 (2): 121-127. |
| [9] | 陈宝春, 叶琳. 我国混凝土拱桥现状调查与发展方向分析[J]. 中外公路, 2008(4):89-96. CHEN Bao-chun, YE Lin. Analysis of Situation and Development of Concrete Arch Bridges in China[J]. Journal of China & Foreign Highway, 2008 (4): 89-96. |
| [10] | 盛叶. 哑铃形钢管混凝土拱桥设计参数取值分析[J]. 贵州大学学报:自然科学版, 2010,27(4): 114-116. SHENG Ye. Parameter Analysis on Concrete-filled Steel Tubular Arch Bridge with Dumbbell Shape [J]. Journal of Guizhou University :Natural Science Edition, 2010,27 (4): 114-116. |
| [11] | DL/T5085—1999, 钢-混凝土组合结构设计规程[S]. DL/T5085—1999, Code for Design of Steel-concrete Composite Structure [S]. |
| [12] | PAN Y, AGRAWAL A K, GHOSN M,et al. Seismic Fragility of Multispan Simply Supported Steel Highway Bridges in New York State. I: Bridge Modeling, Parametric Analysis and Retrofit Design[J]. Journal of Bridge Engineering, 2010,15(5): 448-461. |
| [13] | JTG D60—2004,公路桥涵设计通用规范 [S]. JTG D60—2004,General Code of Design of Highway Bridges and Culverts [S]. |
| [14] | GB18306—2001,中国地震动反应谱特征周期区划图[S]. GB18306—2001, Map of Spectral Characteristics Period of Ground Motion Response in China [S]. |
| [15] | JTJ 004—2005,公路桥梁抗震设计规范[S]. JTJ 004—2005,Code of Seismic Design for Highway Bridges [S]. |
| [16] | CORNELL C A, JALAYER F, HAMBURGER R O, et al. Probabilistic Basis for 2000 SAC Federal Emergency Management Agency Steel Moment Frame Guidelines[J]. |
| [17] | 李树桢.地震灾害评估[M].北京:地震出版社, 1996. LI Shu-zhen. Earthquake Damage Estimation [M]. Beijing: Earthquake Press, 1996. |
| [18] | GB /T18208.3—2000,地震现场工作 第三部分:调查规范[S]. GB /T18208.3—2000, Post-earthquake Field Works—part3:Code for Field Survey [S]. |
| [19] | 谢开仲,吕文高,覃乐勤,等. 钢管混凝土拱桥地震破坏评估研究[J].中国公路学报, 2012,25(2):53-59. XIE Kai-zhong, LV Wen-gao, QIN Le-qin, et al. Research on Seismic Damage Evaluation of CFST Arch Bridges[J]. China Journal of Highway and Transport, 2012,25(2):53-59. |
| [20] | JTG/T B02-01—2008,公路桥梁抗震设计细则[S]. JTG/T B02-01—2008,Guidelines for Seismic Design of Highway Bridges[S]. |
| [21] | PAN Y, AGRAWAL AK, GHOSN M,et al. Seismic Fragility of Multispan Simply Supported Steel Highway Bridges in New York State. Ⅱ: Bridge Modeling, Parametric Analysis, and Retrofit Design[J]. Journal of Bridge Engineering, 2010,15(5): 462-472. |
 2015, Vol. 31
2015, Vol. 31