жү©еұ•еҠҹиғҪ
ж–Үз« дҝЎжҒҜ
- жұӘдёңжһ—, еј дјҹ
- WANG Dong-lin, ZHANG Wei
- жӮ¬зҙўжЎҘдё»зјҶжё©еәҰеңәи®Ўз®—жЁЎеһӢжһ„е»әеҲҶжһҗ
- Analysis of Temperature Field Calculation Modelling of Main Cables of Suspension Bridge
- е…¬и·ҜдәӨйҖҡ科жҠҖ, 2015, Vol. 31 (8): 66-71
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (8): 66-71
- 10.3969/j.issn.1002-0268.2015.08.012
-
ж–Үз« еҺҶеҸІ
- 收зЁҝж—Ҙжңҹ: 2014-8-31
2. йҮҚеәҶй«ҳйҖҹе…¬и·ҜйӣҶеӣўжңүйҷҗе…¬еҸё, йҮҚеәҶ 401121
2. Chongqing Expressway Group Co., Ltd., Chongqing 401121, China
жӮ¬зҙўжЎҘеңЁеӨ–з•ҢзҺҜеўғеҸҳеҢ–ж—¶пјҢдё»зјҶжё©еәҰеңәеҲҶеёғеҚҒеҲҶеӨҚжқӮпјҢиҖҢдё»зјҶжё©еәҰзҡ„ж”№еҸҳдјҡеј•еҸ‘жӮ¬зҙўжЎҘеҮ дҪ•еҪўзҠ¶зҡ„еҸҳеҢ–пјҢеҰӮзҙўеЎ”еЎ”йЎ¶еҒҸдҪҚгҖҒдё»зјҶзҡ„еһӮеәҰзӯүгҖӮе…ідәҺжЎҘжўҒз»“жһ„жё©еәҰеңәеҸҠе…¶ж•Ҳеә”зҡ„з ”з©¶еңЁжңҖиҝ‘еҮ еҚҒе№ҙеҫ—еҲ°дәҶеҝ«йҖҹеҸ‘еұ•пјҢйғЁеҲҶеӯҰиҖ…еҜ№з®ұжўҒжё©еәҰеңәиҝӣиЎҢдәҶз ”з©¶пјҢLee[1]з ”з©¶дәҶж··еҮқеңҹз®ұжўҒжЎҘж–Ҫе·Ҙйҳ¶ж®өзҡ„жңҖдёҚеҲ©жё©еәҰеңәзЎ®е®ҡж–№жі•пјӣеј дә®дә®гҖҒйӣ·з¬‘зӯү[2, 3, 4, 5]иҝӣиЎҢдәҶж··еҮқеңҹз®ұжўҒзҺ°еңәи§ӮжөӢпјҢеҫ—еҲ°дәҶе…¬и·ҜжЎҘжўҒж··еҮқеңҹз®ұжўҒжІҝжҲӘйқўй«ҳеәҰзҡ„жё©еәҰеҲҶеёғ规еҫӢпјӣпјўarrзӯү[6, 7]з ”з©¶дәҶж··еҮқеңҹз®ұжўҒжё©е·®еҸҳеҢ–еҜ№е…¶з»“жһ„жҖ§иғҪзҡ„еҪұе“ҚпјӣеҗҢжөҺеӨ§еӯҰжҪҳж°ёд»ҒеҚҡеЈ«еҲ©з”Ёж—Ҙжң¬еӯҰиҖ…зҡ„иҜ•йӘҢгҖҒж•°жҚ®дҪңдёәиҫ№з•ҢжқЎд»¶пјҢйҮҮз”Ёе…¶иҜ•йӘҢж•°жҚ®е№¶йҖҡиҝҮзғӯе№іиЎЎж–№зЁӢзҡ„жҺЁеҜје’Ңзј–зЁӢпјҢжҸҗдҫӣдәҶдёҖз§Қдё»зјҶжЁӘжҲӘйқўе№іеқҮжё©еәҰзҡ„е®һз”Ёи®Ўз®—ж–№жі• [8]пјӣиғЎеҲ©е№ізӯүи®Ёи®әдәҶжӮ¬зҙўжЎҘжё©еәҰеҸҳеҢ–еҜ№ж–Ҫе·ҘиҝҮзЁӢзҡ„еҪұе“Қ[9, 10, 11]гҖӮз»јдёҠжүҖиҝ°пјҢзӣ®еүҚеӣҪеҶ…зҡ„еӯҰиҖ…еҜ№жӮ¬зҙўжЎҘжё©еәҰеңәеҸҠе…¶ж•Ҳеә”з ”з©¶йғҪйқһеёёйҮҚи§ҶпјҢдҪҶеҸӘжҳҜеҒҸйҮҚдәҺз®ұжўҒеҶ…зҡ„жё©еәҰеңәж•Ҳеә”з ”з©¶пјҢй’ҲеҜ№дё»зјҶжё©еәҰеңәз ”з©¶еҸӘиғҪдҫқйқ зәҝжҖ§еҒҮи®ҫпјҢжҲ–еҒҮи®ҫеҸӘиҖғиҷ‘жҹҗдёҖеӣ зҙ пјҢзјәд№Ҹзі»з»ҹзҡ„гҖҒе®һз”ЁжҖ§зҡ„жё©еәҰеңәи®Ўз®—ж–№жі•гҖӮ
жң¬ж–ҮдҫқжүҳжҹҗжӮ¬зҙўжЎҘпјҢйҖҡиҝҮ1вҲ¶1жЁЎеһӢиҜ•йӘҢиҺ·еҸ–зӣёе…іеҸӮж•°пјҢ并еңЁе»әз«Ӣдё»зјҶзғӯдј еҜјйқһзЁіжҖҒеҫ®еҲҶж–№зЁӢеҸҠзү№е®ҡиҫ№з•ҢжқЎд»¶зҡ„еҹәзЎҖдёҠпјҢз ”з©¶е’ҢжұӮи§ЈзҺҜеўғжқЎд»¶дёҺдё»зјҶжё©еәҰеңәзҡ„еҮҪж•°е…ізі»пјҢжҺўзҙўе»әз«Ӣе…·жңүжҷ®йҖӮжҖ§зҡ„дё»зјҶжё©еәҰйў„жөӢжЁЎеһӢгҖӮ
1 дё»зјҶзғӯеҠӣеӯҰж–№зЁӢж №жҚ®дё»зјҶзҡ„еҸ—зғӯзү№жҖ§пјҢеҸҜе°Ҷдё»зјҶжё©еәҰеңәзҡ„еҸҳеҢ–и§Ҷдёәзғӯдј еҜјй—®йўҳпјҢжҢүз…§еӮ…йҮҢеҸ¶е®ҡеҫӢпјҢжҹұеқҗж ҮдёӢзҡ„дё»зјҶйқһзЁіжҖҒзғӯдј еҜјеҫ®еҲҶж–№зЁӢдёә[12]пјҡ
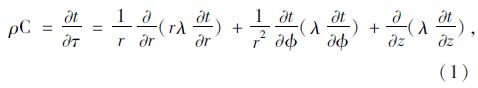
дёәжұӮи§Јдё»зјҶеҫ®еҲҶж–№зЁӢпјҢйҰ–е…ҲйңҖйҖҡиҝҮиҜ•йӘҢпјҢжұӮеҫ—дё»зјҶзӣёе…ізғӯзү©жҖ§еҸӮж•°[13]гҖӮдёәдәҶеҜ№жҜ”е’ҢйӘҢиҜҒпјҢдё»зјҶиҜ•йӘҢжЁЎеһӢйҮҮз”ЁдёӨз§ҚпјҢжЁЎеһӢ1дёәзӣҙеҫ„0.38 mе’ҢжЁЎеһӢ2дёәзӣҙеҫ„0.525 mпјҢиҜ•йӘҢжЁЎеһӢеӣҫеҰӮеӣҫ 1жүҖзӨәгҖӮжЁЎеһӢй•ҝеәҰдёә2 200 mmгҖӮеңЁдё»зјҶжҲӘйқўеёғзҪ®жё©еәҰдј ж„ҹеҷЁжөӢзӮ№гҖӮ

|
| еӣҫ 1 дё»зјҶиҜ•йӘҢжЁЎеһӢ Fig. 1 ain cable test model |
жң¬иҜ•йӘҢжөӢиҜ•зҡ„жҳҜдё»зјҶж•ҙдёӘжҲӘйқўзҡ„е№іеқҮеҜјзғӯзі»ж•°гҖӮиҜ•йӘҢдёҖе…ұи®ҫи®ЎдәҶ3дёӘе·ҘеҶөпјҢиҜ•йӘҢз»јеҗҲжөӢиҜ•з»“жһңеҰӮиЎЁ 1жүҖзӨәгҖӮе…¶дёӯеңЁе·ҘеҶө1дё»зјҶдёӯеҝғеҠ зғӯеҠҹзҺҮ248 WдёӢи®Ўз®—еҖјдёҺе®һжөӢеҖјеҜ№жҜ”и§ҒиЎЁ 2гҖӮ
| е·ҘеҶө | еҜјзғӯзі»ж•°О»/[WВ·(mВ·в„ғ)-1] | ||
| 第1ж¬Ў | 第2ж¬Ў | е№іеқҮеҖј | |
| 1 | 1.03 | 1.18 | 1.11 |
| 2 | 1.11 | 1.2 | 1.16 |
| 3 | 1.34 | вҖ” | 1.34 |
| е№іеқҮеҖј | 1.2 | ||
| жөӢзӮ№дҪҚзҪ®R/m | и®Ўз®—еҖј | е®һжөӢеҖј | иҜҜе·®/% |
| 0.05 | 49.44 | 48.69 | -1.5 |
| 0.06 | 47.48 | 46.12 | -3 |
| 0.10 | 39.11 | 37.37 | -4.7 |
| 0.11 | 37.16 | 35.76 | -3.9 |
еҸҜи§Ғе·®еҲ«еңЁ5пј…д»ҘдёӢпјҢеҗ»еҗҲиүҜеҘҪпјҢиҝҷиҜҙжҳҺиҜ•йӘҢжөӢиҜ•иҫҫеҲ°дәҶзЁіжҖҒпјҢз»“жһңжҳҜеҮҶзЎ®еҸҜдҝЎзҡ„гҖӮ
2.2 зһ¬жҖҒжөӢиҜ•зһ¬жҖҒжөӢиҜ•ж–№жі•жҳҜйҖҡиҝҮжөӢиҜ•жё©еәҰ-ж—¶й—ҙжӣІзәҝпјҢжӣІзәҝж–ңзҺҮеҹәжң¬дҝқжҢҒеёёж•°зҡ„ж—¶ж®өдёәдё»зјҶзі»з»ҹиҫҫеҲ°еҮҶзЁіжҖҒзҡ„ж ҮеҮҶгҖӮ
еҲ©з”ЁиҜ•йӘҢжөӢиҜ•ж•°жҚ®пјҢи®Ўз®—еҗ„дёӘе·ҘеҶөзҡ„зӣёе…іеҸӮж•°еҸҠзғӯжү©ж•Јзі»ж•°еҰӮиЎЁ 3жүҖзӨәгҖӮз»јеҗҲдёӨз§ҚжЁЎеһӢ3дёӘе·ҘеҶөпјҢдё»зјҶеңЁе®Өжё©дёӢеҠ зғӯжөӢиҜ•еҫ—еҲ°жҲӘйқўе№іеқҮзғӯжү©ж•Јзі»ж•°дёәпјҡ3.74Г—10-7 m2/sгҖӮ
| йЎ№зӣ® | е·ҘеҶө1 | е·ҘеҶө2 | е·ҘеҶө3 |
| Bi | 0.497 | 0.497 | 0.687 |
| Ој1 | 0.94 | 0.94 | 1.1 |
| ж–ңзҺҮm/пјҲГ—10-5пјү | 1.0 | 1.0 | 0.6 |
| зғӯжү©ж•Јзі»ж•°Оұ/пјҲГ—10-7пјү | 4.0 | 4.0 | 3.48 |
жҢүз…§дј зғӯеӯҰзҗҶи®әпјҢеҜ№дәҺжӮ¬зҙўжЎҘдё»зјҶиҝҷз§Қз»“жһ„еҸ—зғӯзҠ¶еҶөпјҢеҸӘиғҪйҖҡиҝҮзЎ®е®ҡдё»зјҶжҺҘ收зҡ„зғӯжөҒеҜҶеәҰзҡ„ж–№жі•жүҚеҸҜиЎҢпјҢеҚіж №жҚ®дё»зјҶиЎЁйқўзҡ„еӨӘйҳіиҫҗе°„ејәеәҰпјҢи®Ўз®—е…ЁжЎҘдё»зјҶзҡ„жё©еәҰеңәеҲҶеёғжғ…еҶөгҖӮдёәи®Ўз®—дё»зјҶжүҖеҸ—иҫҗе°„пјҢйңҖдҫқжҚ®е…ЁеӣҪеҗ„ең°еҢәзҡ„иҫҗз…§йҮҸз»ҹи®ЎпјҢеҶҚиҖғиҷ‘жЎҘжўҒе…·дҪ“зҡ„ең°зҗҶзә¬еәҰеҸҠдё»зјҶдёҚеҗҢдҪҚзҪ®и§’еәҰзҡ„еҸҳеҢ–жғ…еҶөгҖҒең°еҪўеҪұе“ҚгҖҒеӨ©ж°”зҠ¶еҶөгҖҒең°зҗҶдҪҚзҪ®гҖҒеӯЈиҠӮзӯүеӣ зҙ зҡ„з»јеҗҲж•Ҳеә”пјҢ然еҗҺеҸҜд»ҘеҜјеҮәд»»ж„Ҹең°еҢәгҖҒд»»ж„ҸжЎҘдҪҚж–№еҗ‘дё»зјҶиҫ№з•ҢжқЎд»¶и®Ўз®—[13, 14, 15]гҖӮ
3.1 еӨӘйҳіе…Ҙе°„и§’еӨӘйҳіе…үзәҝдёҺзү©дҪ“еӨ–иЎЁйқўжі•зәҝд№Ӣй—ҙзҡ„еӨ№и§’з§°дёәеӨӘйҳіе…үзәҝзҡ„е…Ҙе°„и§’ОёпјҢзү©дҪ“еҸ—еҲ°зҡ„еӨӘйҳіиҫҗе°„дёҺеӨӘйҳіе…Ҙе°„и§’жңүе…ігҖӮе…Ҙе°„и§’ОёдёәеӨӘйҳіиөӨзә¬и§’ОҙгҖҒең°зҗҶзә¬еәҰПҶгҖҒзү©дҪ“еҖҫж–ңи§’ОІгҖҒеӨӘйҳіж–№дҪҚи§’ОігҖҒеӨӘйҳіж—¶и§’Пүзҡ„еҮҪж•°пјҢеҚіпјҡ
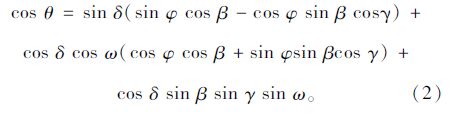
еӨ§ж°”еұӮеӨ–гҖҒе№іеқҮж—Ҙең°и·қзҰ»еӨ„пјҢеһӮзӣҙдәҺиҫҗе°„дј ж’ӯж–№еҗ‘дёҠеҚ•дҪҚйқўз§ҜгҖҒ1 hеҶ…жөӢеҫ—зҡ„еӨӘйҳіиҫҗз…§еәҰдёә1 353 W/m2пјҢз§°дёәеӨӘйҳіеёёж•°пјҢд»ҘGscиЎЁзӨәгҖӮе®һйҷ…дёҠпјҢеӨ§ж°”еұӮеӨ–зҡ„еӨӘйҳіиҫҗе°„ејәеәҰйҡҸзқҖж—Ҙең°и·қзҰ»зҡ„ж”№еҸҳпјҢеңЁВұ3% иҢғеӣҙеҶ…еҸҳеҢ–гҖӮ
3.3 еӨ§ж°”еұӮеҜ№еӨӘйҳіиҫҗе°„зҡ„еҪұе“ҚеҲ°иҫҫең°йқўзҡ„еӨӘйҳіиҫҗе°„дёҺеӨӘйҳіе…үзәҝйҖҡиҝҮеӨ§ж°”еұӮж—¶зҡ„и·Ҝеҫ„й•ҝзҹӯжңүе…іпјҢи·Ҝеҫ„и¶Ҡй•ҝпјҢиЎЁзӨәиў«еӨ§ж°”еҗёж”¶гҖҒеҸҚе°„гҖҒж•Је°„зҡ„еҸҜиғҪи¶ҠеӨҡпјҢеҲ°иҫҫең°йқўзҡ„и¶Ҡе°‘гҖӮжҠҠеӨӘйҳізӣҙе°„е…үзәҝйҖҡиҝҮеӨ§ж°”еұӮж—¶зҡ„е®һйҷ…е…үеӯҰеҺҡеәҰдёҺеӨ§ж°”жі•еҗ‘еҺҡеәҰд№ӢжҜ”з§°дёәеӨ§ж°”иҙЁйҮҸпјҢд»Ҙз¬ҰеҸ·mиЎЁзӨәпјҡ
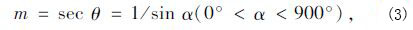
еӨӘйҳіиҫҗе°„еңЁйҖҡиҝҮеӨ§ж°”еұӮеҲ°иҫҫжӮ¬зҙўжЎҘдё»зјҶеҗҺзҡ„ејәеәҰдёҺеҗ„з§Қеӣ зҙ жңүе…іпјҢиҫҗе°„йҮҸжҳҜзЎ®е®ҡдё»зјҶиҫ№з•ҢжқЎд»¶зҡ„йҮҚиҰҒеҸӮж•°д№ӢдёҖгҖӮдёӢйқўйҮҮз”ЁHottleж ҮеҮҶжҷҙеӨ©еӨ§ж°”йҖҸжҳҺеәҰи®Ўз®—жЁЎеһӢпјҡ
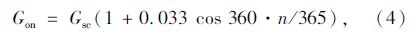
еңЁиҖғиҷ‘жө·жӢ”гҖҒж°”еҖҷзү№еҫҒд»ҘеҸҠеӨ§ж°”иҙЁйҮҸдҝ®жӯЈеҗҺзҡ„зӣҙе°„иҫҗе°„ејәеәҰгҖҒж•Је°„иҫҗе°„ејәеәҰе’ҢжҖ»иҫҗе°„ејәеәҰеҲҶеҲ«дёәпјҡ
ж°ҙе№ійқўдёҠзҡ„зӣҙе°„иҫҗе°„ејәеәҰGc,bдёәпјҡ
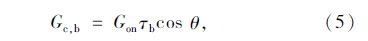
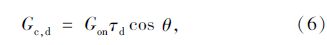
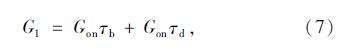

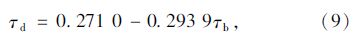
еҪ“жө·жӢ”й«ҳеәҰе°ҸдәҺ2.5 kmж—¶пјҢеҸҜйҰ–е…Ҳз®—еҮәзӣёеә”зҡ„a0*пјҢa1*пјҢk*пјҢеҶҚйҖҡиҝҮиҖғиҷ‘ж°”еҖҷзұ»еһӢзҡ„дҝ®жӯЈзі»ж•°r0=a0/a0*пјҢr1= a1/a1*пјҢrk= k /k*пјҢжңҖеҗҺжұӮеҮәa0пјҢa1е’Ңkпјӣa0*пјҢa1*е’Ңk*зҡ„и®Ўз®—е…¬ејҸдёәпјҡ
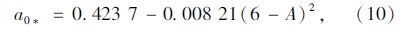
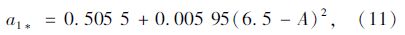
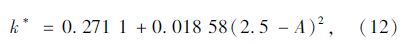
| ж°”еҖҷзұ»еһӢ | r0 | r1 | rk |
| дәҡзғӯеёҰ | 0.95 | 0.98 | 1.02 |
| дёӯзӯүзә¬еәҰпјҢеӨҸеӨ© | 0.97 | 0.99 | 1.02 |
| й«ҳзә¬еәҰпјҢеӨҸеӨ© | 0.99 | 0.99 | 1.01 |
| дёӯзӯүзә¬еәҰпјҢеҶ¬еӨ© | 1.03 | 1.01 | 1 |
еңЁиҖғиҷ‘дёҖеӨ©дёӯзҡ„дә‘йҮҸгҖҒеұұеҢәйҒ®жҢЎж•Ҳеә”зӯүеӣ зҙ пјҢд№ҳд»Ҙзӣёеә”зҡ„йҮҮз”Ёдҝ®жӯЈеӣ еӯҗеҫ—жҖ»иҫҗз…§еәҰG2пјҡ
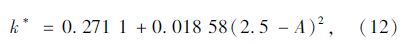
жҠҠдё»зјҶиЎЁйқўзңӢжҲҗзҗҶжғіеңҶжҹұйқўпјҢеҲҷеҸҜд»Ҙд»Ҙдё»зјҶиЎЁйқўд»»ж„ҸдёҖзӮ№дҪҚзҪ®пјҲx,y,zпјүдҪңиҜҘзӮ№зҡ„еҲҮйқўпјҢеҒҮи®ҫеҲҮйқўеҖҫи§’дёәОІпјҢе…¶жі•зәҝеңЁж°ҙе№ійқўзҡ„жҠ•еҪұдёҺжӯЈеҚ—ж–№еҗ‘зҡ„еӨ№и§’дёәОіпјҢиҖғиҷ‘жЎҘжўҒзҡ„ж–№дҪҚгҖҒж—¶й—ҙд»ҘеҸҠдё»зјҶдёҠзҡ„и®Ўз®—дҪҚзҪ®пјҢеҖҫж–ңи§’еәҰзӯүдҝ®жӯЈпјҢеҫ—еҲ°зҡ„дё»зјҶиЎЁйқўеҗёж”¶зҡ„зӯүж•ҲеӨӘйҳіиҫҗе°„иғҪпјҡ

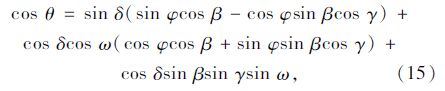
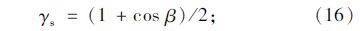
е…ідәҺеӨӘйҳіж—¶и§’зҡ„и®Ўз®—пјҢйңҖиҰҒзЎ®е®ҡдё»зјҶдёҖеӨ©дёӯзҡ„жңүж•Ҳж—Ҙз…§ж—¶й—ҙгҖӮ
еӨӘйҳіж—¶и§’пјҡ
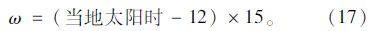
еңЁеӨӘйҳіиҫҗе°„е…·дҪ“и®Ўз®—дёӯпјҢеҪ“ең°еӨӘйҳіж—¶зҡ„жңүж•ҲеҸ–еҖјиҢғеӣҙпјҡпјҲж—ҘеҮәж—¶й—ҙпјҢж—ҘиҗҪж—¶й—ҙпјүпјҢе…¶дёҺж ҮеҮҶж—¶й—ҙзҡ„жҚўз®—е…¬ејҸеҰӮдёӢпјҡ

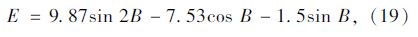
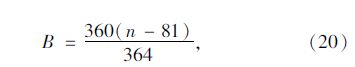
е…ідәҺеӨӘйҳій«ҳеәҰи§’пјҢи®Ўз®—е…¬ејҸдёәпјҡ
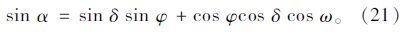
еҪ“ең°зҡ„иөӨзә¬и§’пјҡ
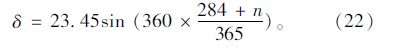
иҖғиҷ‘еҲ°жӮ¬зҙўжЎҘзҡ„е°әеҜёд»ҘеҸҠдё»зјҶзҡ„дҪҚзҪ®иҫғй«ҳпјҢдёҖиҲ¬жғ…еҶөдёӢеҸҜдёҚиҖғиҷ‘ең°еҪўеҜ№жЎҘжўҒдё»зјҶзҡ„йҒ®жҢЎж•Ҳеә”[16]гҖӮ
дёҠйқўд»Ӣз»Қзҡ„дёҖиҲ¬ж–№жі•пјҢе…¶дёӯж¶үеҸҠеҲ°и®Ўз®—зӮ№еҲҮйқўзҡ„еҖҫж–ңи§’ОІе’Ңж–№дҪҚи§’Оізҡ„и®Ўз®—пјҢе®ғ们дёҺи®Ўз®—зӮ№зҡ„з©әй—ҙеқҗж Үжңүе…іпјҢеҜ№дәҺжҜҸдёҖдёӘдҪҚзҪ®ж•°еҖјеқҮдёҚдёҖж ·пјҢи®Ўз®—еҚҒеҲҶеӨҚжқӮгҖӮ
еҒҮи®ҫдё»зјҶзәҝеһӢдёәдәҢз»ҙжҠӣзү©зәҝжҲ–пјҲеҲҶж®өпјүжӮ¬й“ҫзәҝпјҢдё”дёәиҝһз»ӯеҮҪж•°пјҢд»Ҙи·ЁдёӯжңҖдҪҺзӮ№дёәеқҗж ҮеҺҹзӮ№пјҢеҒҮи®ҫе…¶ж–№зЁӢдёәпјҡ
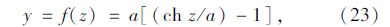
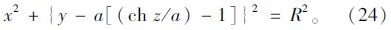
и®Ўз®—зӮ№ж–№дҪҚи§’ОійҡҸзқҖи®Ўз®—зӮ№еңЁдё»зјҶжЁӘжҲӘйқўзҡ„дҪҚзҪ®еҸҳеҢ–пјҢеҸҳеҢ–иҢғеӣҙдёәпјҲ0В°пјҢ360В°пјүпјӣиҖҢи®Ўз®—зӮ№еҲҮйқўеҖҫж–ңи§’ОІдёҚд»…еңЁдё»зјҶжЁӘжҲӘйқўжІҝдё»зјҶеңҶе‘ЁеҸҳеҢ–пјҢиҖҢдё”иҝҳжІҝзқҖдё»зјҶиҪҙзәҝж–№еҗ‘йҡҸзқҖдё»зјҶзәҝеҪўеҸҳеҢ–иҖҢеҸҳеҢ–пјҢОІи§’еҸҜд»Ҙз”ұи®Ўз®—зӮ№еңЁдё»зјҶзҡ„жЁӘжҲӘйқўеңҶе‘ЁдёҠзҡ„еҸҳеҢ–и§’еәҰОІ1еҸҠжІҝжЎҘжўҒзәөеҗ‘зҡ„еҸҳеҢ–и§’еәҰОІ2иҝӣиЎҢи®Ўз®—еҫ—еҲ°пјҡ
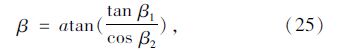
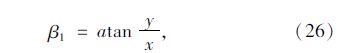
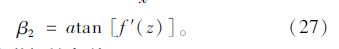
зЎ®е®ҡдё»зјҶдј зғӯеӯҰеҒҸеҫ®еҲҶж–№зЁӢз»„зҡ„е®ҡи§ЈжқЎд»¶йҷӨдәҶиҫ№з•ҢжқЎд»¶еӨ–пјҢиҝҳйңҖиҰҒзЎ®е®ҡе…¶еҲқе§ӢжқЎд»¶пјҢеҚіеңЁи®Ўз®—ејҖе§Ӣж—¶еҲ»ж•ҙдёӘз»“жһ„зҡ„еҲқе§Ӣжё©еәҰпјҢз”Ёе…¬ејҸиЎЁзӨәдёәпјҡ
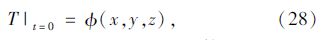
жң¬ж–Үд»ҘжҹҗеӨ§жЎҘдёәдҫӢиҝӣиЎҢжЎҘеқҖең°еҢәе®һең°зҺ°еңәиҜ•йӘҢдёҺи®Ўз®—еҜ№жҜ”пјҢжөӢиҜ•ж—¶й—ҙдёәеӨҸеӯЈ7вҖ”8жңҲд»ҪпјҢиҜ•йӘҢжЁЎеһӢдёә2.2 mй•ҝзӣҙзәҝдё»зјҶзҙўж®өпјҢдё»зјҶзҙўж®өзҡ„иҪҙзәҝжІҝеҪ“ең°жӯЈеҚ—еҢ—ж–№еҗ‘гҖӮиҜҘжғ…еҶөеҸҜд»ҘжҠҠдё»зјҶзңӢжҲҗжҳҜе№ійқўдәҢз»ҙжЁЎеһӢпјҢжЎҘеқҖең°еҢәе®һжөӢжңүж•Ҳж—Ҙз…§ж—¶й—ҙеҸ–12 hпјҡеҚіж—©дёҠж—ҘеҮәз…§е°„еҲ°дё»зјҶзҡ„ж—¶й—ҙдёә6пјҡ30пјҢж—ҘиҗҪйҳіе…үж—¶й—ҙдёә18пјҡ30гҖӮи®Ўз®—иө·е§ӢзӮ№еҸ–дёәеҮҢжҷЁ0пјҡ00пјҢжЎҘеқҖең°еҢәзә¬еәҰПҶпјқ29.5В°NгҖӮжЎҘеқҖең°еҢәеұһдәҺдәҡзғӯеёҰж°”еҖҷпјҢиҜ•йӘҢдҪҚзҪ®жө·жӢ”еҸ–300 mгҖӮ
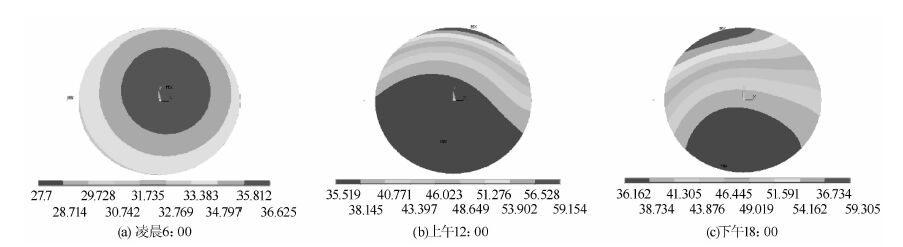
еӣҫ 2з»ҷеҮәдәҶжҷҙеӨ©жғ…еҶөдёӢпјҢи®Ўз®—еҫ—еҲ°зҡ„жҹҗж—Ҙеҗ„ж—¶й—ҙж®өдё»зјҶжҲӘйқўе…ёеһӢжё©еәҰеҲҶеёғеӣҫ [17]гҖӮ д»Һеӣҫ 2зңӢеҮәпјҢжҲӘйқўдёҠеҚҠйғЁеҲҶжё©еәҰй«ҳдәҺдёӢеҚҠйғЁеҲҶпјҢзҷҪеӨ©жңҖй«ҳжё©еәҰеҮәзҺ°еңЁиҝҺйҳійқўпјҢжҷҡдёҠжңҖй«ҳжё©еәҰеҮәзҺ°еңЁжҲӘйқўеҶ…йғЁпјҢиҝҷдёҺе®һжөӢзҡ„з»“и®әдёҖиҮҙгҖӮзҷҪеӨ©жңҖй«ҳжё©еәҰд»ҺдёӯеҚҲ12зӮ№еҲ°дёӢеҚҲ4зӮ№е·ҰеҸідҫқж¬ЎжІҝиҝҺйҳійқўеҮәзҺ°пјҢжңҖй«ҳжҺҘиҝ‘60 в„ғгҖӮеҮ дёӘе…ёеһӢж—¶еҲ»зҡ„и®Ўз®—еҖјдёҺжөӢзӮ№е®һжөӢеҖјзҡ„еҜ№жҜ”и§ҒиЎЁ 5гҖӮ
|
| еӣҫ 2 дё»зјҶжЁЎеһӢжҲӘйқўдёҚеҗҢж—¶й—ҙжё©еәҰеҲҶеёғ(еҚ•дҪҚ:в„ғ) Fig. 2 emperature distribution in section of main cable model at different time(unit:в„ғ) |
| ж—¶еҲ» | дёҠеҚҲ9пјҡ00 | ж—¶еҲ» | дёӢеҚҲ15пјҡ00 | ||||
| жөӢзӮ№еҸ· | е®һжөӢеҖј | и®Ўз®—еҖј | иҜҜе·®/пј… | жөӢзӮ№еҸ· | е®һжөӢеҖј | и®Ўз®—еҖј | иҜҜе·®/пј… |
| 2 | 35.6 | 37.5 | 5.3 | 2 | 44.2 | 41.7 | 2.7 |
| 3 | 35.6 | 36.4 | 2.4 | 3 | 39.5 | 37.9 | 3.1 |
| 4 | 35.3 | 37.5 | 6.4 | 4 | 42.3 | 40.0 | -0.6 |
| 5 | 34.9 | 36.3 | 4.0 | 5 | 39.4 | 37.6 | 2.2 |
| 6 | 35.2 | 35.5 | 0.7 | 6 | 40.4 | 36.4 | -4.4 |
| 7 | 35.3 | 35.8 | 1.4 | 7 | 38.4 | 36.3 | -0.3 |
| 8 | 35 | 35.1 | 0.3 | 8 | 37.8 | 35.5 | -1.0 |
| 9 | 35.7 | 35.7 | 0.0 | 9 | 36.7 | 35.8 | 0.8 |
| 10 | 35.4 | 35.5 | 0.2 | 10 | 36.8 | 35.7 | 0.7 |
д»ҺиЎЁ 5еҸҜи§ҒпјҢеҜ№дәҺжҲӘйқўжөӢзӮ№зҡ„жё©еәҰеӨ§е°ҸеҲҶеёғеҸҠеҸҳеҢ–и¶ӢеҠҝпјҢи®Ўз®—еҖјдёҺе®һжөӢеҖјеҗ»еҗҲеҫ—йқһеёёеҘҪпјҢиҖҢеӨ§йғЁеҲҶжөӢзӮ№е·®еҖјеқҮеңЁ5пј…д»ҘеҶ…пјҢиҜҜе·®иҫғеӨ§дҪҚзҪ®д№ҹжҳҜеҹәжң¬дҪҚдәҺдё»зјҶиЎЁйқўйқ иҝ‘ең°иЎЁеӨ„пјҢиҝҷиҜҙжҳҺжҳҜз”ұдәҺең°йқўзҡ„еҸҚе°„зғӯиҫҗе°„жүҖйҖ жҲҗзҡ„иҜҜе·®гҖӮе®һжөӢжңҖй«ҳжё©еәҰйҡҸж—¶й—ҙдҫқж¬ЎжІҝиҝҺйҳійқўеҮәзҺ°пјҢжңҖй«ҳиҫҫеҲ°60 в„ғд»ҘдёҠгҖӮ
жӯӨеӨ–пјҢеҲҶжһҗиҜҜе·®дә§з”ҹеҺҹеӣ пјҢжқҘжәҗдё»иҰҒжңүд»ҘдёӢдёӨдёӘж–№йқўпјҡ(1)жөӢиҜ•иҜҜе·®пјҢеҢ…жӢ¬жөӢиҜ•д»ӘеҷЁгҖҒжөӢиҜ•ж–№жі•зӯүеј•е…Ҙзҡ„жөӢиҜ•иҜҜе·®пјӣ(2)и®Ўз®—иҜҜе·®пјҢдё»иҰҒжңүи®Ўз®—жЁЎеһӢзҡ„дёҖдәӣз®ҖеҢ–еҒҮи®ҫиҜҜе·®пјҢзғӯзү©жҖ§еҸӮж•°иҜҜе·®гҖҒеҲқе§ӢжқЎд»¶еҸҠиҫ№з•ҢжқЎд»¶зҡ„з®ҖеҢ–еҒҮе®ҡеёҰжқҘзҡ„иҜҜе·®е’Ңи®Ўз®—зӯүж•ҲжЁЎеһӢеёҰжқҘзҡ„зӯүж•ҲиҜҜе·®зӯүгҖӮ
5 з»“и®әжң¬ж–ҮеҜ№жӮ¬зҙўжЎҘдё»зјҶжё©еәҰеңәиҝӣиЎҢдәҶиҫғдёәзі»з»ҹзҡ„з ”з©¶пјҢе®һйҷ…дё»зјҶз»“жһ„зҡ„зғӯзү©жҖ§еҸӮж•°жөӢиҜ•еӣҪеҶ…е°ҡеұһз©әзҷҪгҖӮ
пјҲ1пјүйҖҡиҝҮдё»зјҶжЁЎеһӢзҡ„дёҖзі»еҲ—иҜ•йӘҢжөӢиҜ•пјҢйҒөеҫӘдј зғӯеӯҰзҗҶи®әе’ҢиҜ•йӘҢгҖҒдј зғӯеӯҰж–№жі•пјҢжҠҠдё»зјҶзңӢжҲҗеҫ„еҗ‘дёҖз»ҙз»“жһ„пјҢи®Ўз®—еҫ—еҲ°дәҶдё»зјҶиҝҷз§ҚеӨҚеҗҲжқҗж–ҷеңЁе®Өжё©дёӢзҡ„зғӯжү©ж•ЈеҸӮж•°гҖҒе№іеқҮиЎЁи§Ӯзғӯжү©ж•Јзі»ж•°гҖӮйҖҡиҝҮи®Ўз®—йӘҢиҜҒд»ҘеҸҠеҗҢеӣҪеӨ–зӣёе…іиҜ•йӘҢз»“жһңзҡ„еҜ№жҜ”еҲҶжһҗпјҢи®ӨдёәжЁЎеһӢиҜ•йӘҢеҫ—еҲ°зҡ„дё»зјҶеҗ„зғӯзү©жҖ§еҸӮж•°з»“жһңж•°жҚ®жҳҜеҮҶзЎ®еҸҜдҝЎзҡ„пјҢеҸҰеӨ–пјҢз”ұдәҺдё»зјҶжЁЎеһӢжқҗж–ҷе’Ңеӯ”йҡҷзҺҮйғҪдёҺе®һжЎҘеҸҠ规иҢғзӣёдёҖиҮҙпјҢеӣ жӯӨпјҢжөӢиҜ•зғӯзү©жҖ§еҸӮж•°еҸҜдҪңдёәеҗҺз»ӯе·ҘдҪңзҡ„еҹәзЎҖпјҢд№ҹеҸҜз”ЁдәҺжӮ¬зҙўжЎҘдё»зјҶжё©еәҰеңәи®Ўз®—еҲҶжһҗгҖӮ
(2)зі»з»ҹең°жҺЁеҜјдәҶдё»зјҶеңЁеӨӘйҳіиҫҗе°„дёӢзҡ„жё©еәҰеңәи®Ўз®—ж–№жі•пјҢдё»иҰҒеҢ…жӢ¬дё»зјҶзҡ„иҫ№з•ҢжқЎд»¶еӨ„зҗҶгҖҒдё»зјҶзҡ„еҲқе§ӢжқЎд»¶д»ҘеҸҠдё»зјҶзҡ„и®Ўз®—жЁЎеһӢзӯүпјҢеҲҶжһҗеҫ—еҲ°дәҶдёҖеҘ—дё»зјҶжё©еәҰеңәзҡ„жҷ®йҖӮи®Ўз®—ж–№жі•пјҢиҝӣиЎҢдәҶжЎҘеқҖең°еҢәзҺҜеўғдёӢзҡ„дё»зјҶеңЁеӨӘйҳіиҫҗе°„дёӢзҡ„жё©еәҰеңәе“Қеә”и®Ўз®—е’ҢйӘҢиҜҒгҖӮз»“жһңиЎЁжҳҺиҜҘи®Ўз®—ж–№жі•жҳҜеҮҶзЎ®еҸҜйқ зҡ„пјҢиҝҷдәӣз ”з©¶з»“и®әз»ҷеӨ§и·ЁеәҰжӮ¬зҙўжЎҘдё»зјҶз»“жһ„зҡ„жё©еәҰж•Ҳеә”з ”з©¶жҸҗдҫӣдәҶзӣёе…ізҗҶи®әеҲҶжһҗеҹәзЎҖгҖӮ
(3)и®Ўз®—иЎЁжҳҺеҪ“йҮҮз”Ёдј з»ҹж–№жі•пјҢз”ұиЎЁйқўжөӢзӮ№е№іеқҮеҖјиҺ·еҫ—зҡ„дё»зјҶжҲӘйқўе№іеқҮжё©еәҰдёҺе®һйҷ…жҲӘйқўзҡ„е№іеқҮжё©еәҰеҖјзҡ„иҜҜе·®дёҚеҸҜеҝҪз•ҘпјҢдёәдәҶжҸҗй«ҳдё»зјҶжһ¶и®ҫзІҫеәҰпјҢе»әи®®ж–Ҫе·Ҙж—¶йҮҮз”Ёжҷ®йҖӮи®Ўз®—ж–№жі•иҺ·еҫ—зңҹе®һзҡ„жҲӘйқўзҡ„е№іеқҮжё©еәҰгҖӮ
| [1] | LEE J H. Investigation of Extreme Environmental Conditions and Design Thermal Gradients During Construction for Prestressed Concrete Bridge Girders [J].Journal of Bridge Engineering, 2012,17(3):547-556. |
| [2] | еј дә®дә®,жқЁзЈҠ,жқЁиҪ¬иҝҗ,зӯү.еӨ§и·Ёж··еҮқеңҹз®ұжўҒжё©еәҰеңәеҲҶжһҗ[J].еңҹжңЁе»әзӯ‘дёҺзҺҜеўғе·ҘзЁӢ,2011,33(1):36-42. ZHANG Liang-liang,YANG Lei,YANG Zhuan-yun, et al. Temperature Field Analysis of Long-span Concrete Box Girders[J].Journal of Civil, Architectural & Environmental Engineering,2011,33(1):36-42. |
| [3] | йӣ·з¬‘,еҸ¶и§Ғжӣҷ,зҺӢжҜ….ж—Ҙз…§дҪңз”ЁдёӢж··еҮқеңҹз®ұжўҒзҡ„жё©е·®д»ЈиЎЁеҖј[J].дёңеҚ—еӨ§еӯҰеӯҰжҠҘ:иҮӘ然科еӯҰзүҲ,2008, 38(6):1105-1109. LEI Xiao,YE Jian-shu,WANG Yi. Representative Value of Solar Thermal Difference Effect on PC Box-girder[J].Journal of Southeast University: Natural Science Edition, 2008, 38(6):1105-1109. |
| [4] | жұӘеү‘,ж–№еҝ—.ж··еҮқеңҹз®ұжўҒжЎҘзҡ„жё©еәҰеңәеҲҶжһҗ[J].ж№–еҚ—еӨ§еӯҰеӯҰжҠҘ:иҮӘ然科еӯҰзүҲ,2008, 35( 4): 23-28. WANG Jian,FANG Zhi. Temperature Variation of Concrete Box Girder Bridge [J].Journal of Hunan University: Natural Science Edition, 2008, 35(4):23-28. |
| [5] | йӮ“жү¬,жқҺзҲұзҫӨ,дёҒе№јдә®.еӨ§и·ЁжӮ¬зҙўжЎҘжўҒз«ҜдҪҚ移дёҺжё©еәҰзҡ„зӣёе…іжҖ§з ”究еҸҠе…¶еә”з”Ё[J].е…¬и·ҜдәӨйҖҡ科жҠҖ,2009,26(5):54-58. DENG Yang, LI Ai-qun, DING You-liang. Research and Application of Correlation between Beam End Displacement and Temperature of Long-span Suspension Bridge[J].Journal of Highway and Transportation Research and Development, 2009, 26(5):54-58. |
| [6] | BARR P J, STANTON J F, EBERHARD M O. Effects of Temperature Variations on Precast, Prestressed Concrete Bridge Girders [J]. Journal of Bridge Engineering, 2005, 10(2): 186-194. |
| [7] | RADOVANOVIC Z, ULIĆEVIĆ M. Influence of Temperature on Box Girder Bridges [J].Gradevinar,2008,60(2):109-121. |
| [8] | жҪҳж°ёд»Ғ, иҢғз«ӢзЎҖ.жӮ¬зҙўжЎҘж–Ҫе·Ҙдёӯдё»зјҶжЁӘжҲӘйқўе№іеқҮжё©еәҰе®һз”Ёи®Ўз®—жі•[J]. еҗҢжөҺеӨ§еӯҰеӯҰжҠҘ:иҮӘ然科еӯҰзүҲ, 1998, 26 (2): 114-118. PAN Yong-ren, FAN Li-chu. Practical Method for Calculating the Mean Temperature of the Main Cable Section in the Construction Control of Suspension Bridges [J].Journal of Tongji University:Natural Science Edition, 1998,26 (2): 114-118. |
| [9] | зҺӢиҫҫ,еј ж°ёеҒҘ,й»„е№іжҳҺ.еӨ§и·ЁеәҰжӮ¬зҙўжЎҘдё»зјҶж–Ҫе·Ҙжё©еәҰж—¶еҸҳж•Ҳеә”з ”з©¶[J]. е…¬и·ҜдәӨйҖҡ科жҠҖ, 2010,27(12): 72-77. WANG Da, ZHANG Yong-jian, HUANG Ping-ming. Research on Temperature Time-varying Effect of Long-span Suspension Bridge during Main Cable Construction [J]. Journal of Highway and Transportation Research and Development, 2010,27 (12): 72-77. |
| [10] | жһ—дёҖе®Ғ,дҪҷеұҸеӯҷ,жһ—дәҡи¶….жӮ¬зҙўжЎҘжһ¶и®ҫжңҹй—ҙдё»зјҶжё©еәҰжөӢиҜ•з ”究[J].жЎҘжўҒе»әи®ҫ,1997(3):58-66. LIN Yi-ning.YU Ping-sun, LIN Ya-chao. Measurement and Analysis of Temperature of the Main Cable during the Erection of Suspension Bridges [J]. Bridge construction, 1997(3):58-66. |
| [11] | иғЎеҲ©е№і.жӮ¬зҙўжЎҘж–Ҫе·ҘиҝҮзЁӢдёӯдё»зјҶжё©еәҰж•Ҳеә”еҲҶжһҗ[J].дёӯеӣҪе»әи®ҫдҝЎжҒҜ,2003(19):45-47. HU Li-ping. Analysis of Temperature Effect of Main Cables of Suspension Bridge in Construction Process [J]. Information of China Construction, 2003(19):45-47. |
| [12] | еҫҗжө·й№°,иөөе°‘жқ°.жӮ¬зҙўжЎҘдё»зјҶжё©еәҰеңәи®Ўз®—[J].й“ҒйҒ“е·ҘзЁӢеӯҰжҠҘ,2012 (1):45-50. XU Hai-ying, ZHAO Shao-jie. Calculation of Temperature Field of Main Cable of Suspension Bridge[J]. Journal of Railway Engineering Society, 2012 (1):45-50. |
| [13] | жқЁдё–й“ӯ,йҷ¶ж–Үй“Ё.дј зғӯеӯҰ [M]. 4зүҲ.еҢ—дә¬:й«ҳзӯүж•ҷиӮІеҮәзүҲзӨҫ,2006. YANG Shi-ming,TAO Wen-quan. Heat Transfer [M]. 4th ed. Beijing: Higher Education Press,2006. |
| [14] | й»„ж–Үйӣ„.еӨӘйҳіиғҪд№Ӣеә”з”ЁеҸҠзҗҶи®ә[M].еҸ°еҢ—:еҸ°еҢ—еҮәзүҲзӨҫ,1978. HUANG Wen-xiong. Application and Theory of Solar Energy[M]. Taipei:Taipei Press, 1978. |
| [15] | йҮ‘дјҹиүҜ.е·ҘзЁӢиҚ·иҪҪз»„еҗҲзҗҶи®әдёҺеә”з”Ё[M].еҢ—дә¬:жңәжў°е·ҘдёҡеҮәзүҲзӨҫ,2006. JIN Wei-liang. Engineering Load Combination Theory and Application [M].Beijing:China Machine Press, 2006. |
| [16] | еҮҜе°”еҲ«е…Ӣ F. еӨӘйҳіиҫҗе°„еҜ№жЎҘжўҒз»“жһ„зҡ„еҪұе“Қ[M]. еҲҳе…ҙжі•, зӯүиҜ‘. еҢ—дә¬: дёӯеӣҪй“ҒйҒ“еҮәзүҲзӨҫ, 1981. CALEBUICK F. Effect of Solar Radiation on Bridge Structure [M]. LIU Xing-fa, et al. translated. Beijing: China Railway Publishing House, 1981. |
| [17] | еј й№ӨйЈһ. еӨӘйҳіиғҪзғӯеҲ©з”ЁеҺҹзҗҶдёҺи®Ўз®—жңәжЁЎжӢҹ [M].2зүҲ.иҘҝе®ү:иҘҝеҢ—е·ҘдёҡеӨ§еӯҰеҮәзүҲзӨҫ,2007. ZHANG He-fei. Principle of Solar Thermal Utilization and Computer Simulation [M]. 2nd ed. Xi'an: Northwestern Polytechnical University Press, 2007. |
 2015, Vol. 31
2015, Vol. 31
