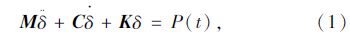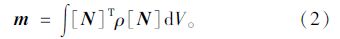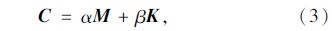扩展功能
文章信息
- 李江, 王晓涛, 余胜军
- LI Jiang, WANG Xiao-tao, YU Sheng-jun
- 不同车速下沥青路面结构的动力响应
- Dynamic Responses of Asphalt Pavement Structure to Different Vehicle Speeds
- 公路交通科技, 2015, Vol. 31 (8): 6-11
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (8): 6-11
- 10.3969/j.issn.1002-0268.2015.08.002
-
文章历史
- 收稿日期: 2015-03-03
2. 道路结构与材料交通行业重点实验室, 北京 100088
2. Key Laboratory for Road Structure & Material of Ministry of Transport, Beijing 100088, China
国内外现行道路设计方法中,一般均是将汽车荷载简化为静力荷载,但现实中汽车总是以一定的速度行驶在路面上,因此分析移动荷载下沥青路面结构动力响应更加具有现实意义。虽然现在随着有限元技术的发展对多层体系的路面在移动荷载下的动力响应有了一定研究,但是多集中在二维模型的研究上,这其实是不够精确的[1]。特别是在长大上坡路段、道路交叉口等地方,交通量大、车速变化大,在频繁制动启动过程中,路面结构内部存在着复杂的应力作用,致使路面经常出现车辙、拥包、推移等早期损坏现象 [2, 3]。本文借助大型有限元软件ABAQUS,建立3D动力有限元模型,通过编写子程序实现车辆荷载的移动,分析车辆以不同速度匀速通过和刹车状态下路面结构的动力响应。
1 理论基础有限元动力学分析的主要过程可包括以下几个步骤:(1)连续体的离散化;(2)选取单元的位移模型;(3)用变分原理导出单元的动力学方程;(4)经整体集合建立总体运动方程;(5)求解运动方程;(6)计算结构的应力应变。从以上步骤可知,和静力学分析比较,在动力分析中,由于惯性力和阻尼力出现在平衡方程中,因此引入了质量矩阵和阻尼矩阵,最后得到的求解方程不是代数方程组而是常微分方程组。其他的计算步骤和静力学分析相同[4, 5, 6, 7, 8]。
应用弹性力学的Hamilton变分原理,近而可得到弹性系统动力问题的有限元基本方程如下:
式中,M,C,K分别为系统的质量矩阵、阻尼矩阵、刚度矩阵;$\ddot \delta $,$\dot \delta $,$\delta $分别为加速度、速度、位移向量;P(t)为移动荷载。
(1)质量矩阵
M为系统质量矩阵,由单元质量矩阵m组合得到,m由式(2)得到:
(2)阻尼矩阵
通常是根据实测资料,由振动过程中结构整体的能量消耗来决定阻尼的近似值,因此不是计算单元的阻尼矩阵,而直接计算结构的整体阻尼矩阵C,一般采用如下的线性关系式,即通常所说的瑞利阻尼,见式(3):
式中α,β均是根据实测资料确定的系数,本文采用文献[5]所给数据。
2 模型建立 2.1 计算参数整个路面的结构基本参数详见表 1(以内蒙某高速公路路面结构为例,沥青混合料模量取值为15 ℃条件下).
在ABAQUS建模时,面层选用扩展的Drucker Prager模型,扩展的Drucker Prager模型的屈服面在π平面上不是圆形的,屈服面的子午面包括线性模型、双曲线模型和指数模型。扩展的Drucker Prager模型具有如下特点:
| 结构层 | 厚度/cm | 混合料类型 | 泊松比 | 密度/(g·cm -3) | 模量/ MPa | α | β |
| 上面层 | 4 | AC-16C | 0.25 | 2.36 | 2000 | 0.4 | 0.005 |
| 中面层 | 5 | AC-20 | 0.25 | 2.36 | 1800 | 0.4 | 0.005 |
| 下面层 | 7 | AC-25 | 0.25 | 2.37 | 1200 | 0.4 | 0.005 |
| 基层 | 20 | 水泥稳定级配碎石 | 0.3 | 2.24 | 3800 | 0.4 | 0.005 |
| 底基层 | 16 | 水泥稳定级配碎石 | 0.35 | 2.24 | 3400 | 0.4 | 0.005 |
| 路基 | 16 | 0.35 | 1.85 | 40 | 0.4 | 0.005 |
(1)适用于模拟材料的蠕变功能来描述材料的长期非弹性变形;(2)考虑了材料的剪胀性;(3)适用于模拟与应变率相关的材料,比如聚合物等;(4)允许材料各向同性硬化或软化;(5)可用来模拟压缩屈服强度远大于拉伸屈服强度的材料,如复合物和聚合物等。
扩展的Drucker Prager模型参数设置为:剪切准则为线性,流动势偏心率为0.1,摩擦角为0,流应力比为1,膨胀角为0。相应的蠕变法则为Drucker Prager时间蠕变法则,面层各层相应的蠕变模型参数由蠕变试验拟合得到[9, 10, 11, 12, 13, 14],详见表 2;硬化法则采用Drucker Prager 时间硬化法则。
| 部位 | 混合料类型 | 时间蠕变模型各参数取值 | ||
| A | n | m | ||
| 上面层 | AC-16C | 1.17E-09 | 0.8 | -7.538 |
| 中面层 | AC-20 | 7.11E-10 | 0.8 | -4.658 |
| 下面层 | AC-25 | 6.79E-10 | 0.8 | -3.428 |
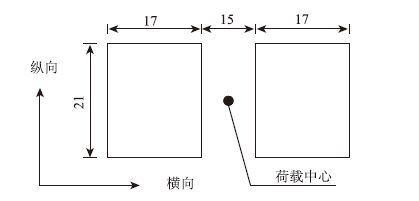
在实际中,车辆行驶在路面上时,路面要承受复杂的垂直力和水平力的共同作用。荷载采用现行公路沥青路面设计规范中标准轴载BZZ-100,为了将问题简化,本文将汽车轮载简化为均布矩形荷载,设计胎压为0.7 MPa,见图 1。匀速行驶时为垂直均布荷载,刹车路段为垂直均布荷载和水平均布荷载。
|
| 图 1 荷载的简化(单位: cm) Fig. 1 Load simplification (unit: cm) |
|
|
在ABAQUS建模过程中为了模拟车辆荷载的移动,在车辆荷载移动方向上设置荷载移动带,路面结构纵向长度为车辆行驶的距离即为移动荷载带的移动方向,简化后的荷载宽度即为移动荷载带的宽度;然后,将移动荷载带细分为小矩形,本文按车轮加载长度的二分之一进行细分,见图 2,移动初始,荷载占据两个小矩形的面积,即图 2中的1和2部分。在移动过程中,荷载移动带方向(行车方向)逐渐向前移动。通过ABAQUS子程序实现荷载的移动,用户子程序是根据ABAQUS提供的相应接口,按照Fortran语法,用户自己编写代码。本文根据所研究问题的需要,编写了施加移动荷载的子程序Dload和Utracload,其中Dload用来施加垂直均布荷载;Utracload用来施加水平均布荷载。荷载的移动速度可以通过子程序中荷载步的时间大小来实现[9]。

|
| 图 2 荷载移动带细化示意图 Fig. 2 Subdivision of load moving strip |
|
|
本文采用的模型尺寸为长×宽×高=10 m×5 m×5 m,层间完全连续,建立3D有限元模型如图 3所示。

|
| 图 3 动力有限元模型 Fig. 3 Dynamic finite element model |
|
|
边界条件:模型左右两侧约束x向水平位移,前后两侧约束z方向水平位移,模型底部为土基采用完全固定约束。
网格划分:荷载作用区域加密网格采用0.01 m×0.01 m×0.01 m的网格尺寸,其他面层部位采用0.02 m×0.02 m×0.02 m网格尺寸,基层与底基层采用0.05 m×0.05 m×0.05 m网格尺寸,土基与垫层采用0.1 m×0.1 m×0.1 m的网格尺寸;采用的单元类型为三维六面体八节点线性减缩积分等参单元(C3D8R)。
3 计算结果分析 3.1 匀速行驶状态下不同车速的结构动力响应研究匀速状态下,速度的变化对沥青路面结构动力响应的影响时,车辆分别以10,30,80,100,120 km/h的速度通过模型,模型中只考虑垂直均布荷载,应力选取的计算点为车轮荷载正下方中心特殊点。
3.1.1 速度对垂直正应力的影响由于不同车速下路面垂直正应力时程曲线图的形状基本类似,只是幅值不同,因此只选取车速为80 km/h时的沥青路面垂直正应力时程曲线图作为代表,见图 4。
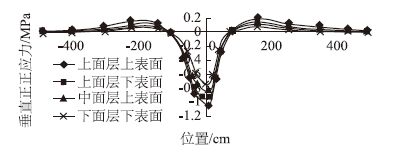
|
| 图 4 车速为80 km/h沥青面层的垂直正应力时程曲线图 Fig. 4 Time history curves of vertical normal stress in |
|
|
由图 2可知,在移动荷载作用下,沥青路面结构的面层主要承受垂直压应力,当荷载靠近计算点位时,出现了很小的拉应力,这种先拉后压的情况与传统的静力分析有明显的区别,尽管沥青路面结构所受的拉应力较小,但是垂直应力的交变特性将会引起路面材料的疲劳破坏;最大垂直压应力出现在面层上表面;随着深度的增加垂直压应力逐渐减小,因而在进行路面铺筑的时候,一定要注意上面层和中面层的压实质量,防止因为进一步压实造成的车辙。对不同车速下的最大垂直压应力进行汇总,为了能够更加直观地反映不同车速下的最大垂直压应力变化规律,以曲线图形式表示,见图 5。
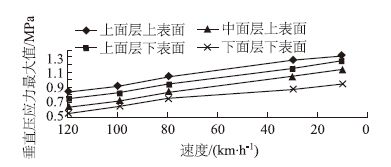
|
| 图 5 最大垂直压应力随车速变化曲线图 Fig. 5 Curves of maximum vertical compressive stress vs. vehicle speed |
|
|
由图 5可知,同一车速下,随着深度的增加,垂直压应力最大值逐渐减小。在移动荷载作用下,最大垂直压应力随着车速的减小逐渐增大,并且基本呈现线性增大的趋势,随着深度的增加最大垂直压应力增大的趋势是在下降的。从数值上看,当速度由120 km/h减小到10 km/h时,上面层上表面最大垂直压应力增大了56.8%,上面层下表面增大了67.7%,中面层上表面增大了77.9%,下面层下表面增大了71.3%。
3.1.2 速度对水平正应力的影响由于不同车速下路面水平正应力时程曲线图的形状基本类似,只是幅值不同,因此只选取车速为80 km/h时的沥青路面水平正应力时程曲线图作为代表,见图 6。
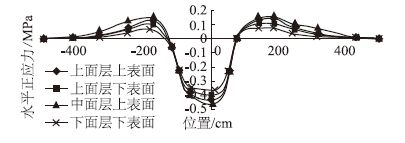
|
| 图 6 车速为80 km/h时沥青面层的水平正应力时程曲线图 Fig. 6 Time history curves of horizontal normal stress in |
|
|
由不同车速下水平正应力的时程曲线图可知,在移动荷载作用下,沥青路面结构的面层既要承受水平拉应力又要承受水平压应力,这种先拉后压的情况与传统的静力分析有明显的区别,这种应力交变特性将会引起路面材料的疲劳破坏;从数值大小上看,面层主要还是承受水平压应力,最大水平压应力出现在中面层上表面;此后随着深度的增加水平最大压应力逐渐减小。对不同车速下的最大水平压应力进行汇总,为了能够更加直观地反映不同车速下的最大水平压应力变化规律,以曲线图形式表示,见图 7。
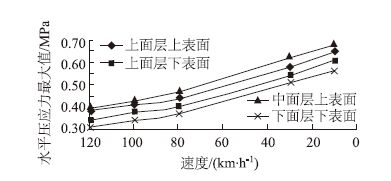
|
| 图 7 最大垂直压应力随车速变化曲线图 Fig. 7 Curves of maximum horizontal compressive stress vs. vehicle speed |
|
|
由图 7可知,同一车速下,水平压应力在中面层出现最大值,然后随着深度的增加而减小。在移动荷载作用下,最大水平压应力随着车速的减小逐渐增大,并且基本呈现线性增大的趋势(在80 km/h以后趋势略有增大)。从数值上看,当速度由120 km/h减小到10 km/h时,上面层上表面最大水平压应力增大了68.1%,上面层下表面增大了78.1%,中面层上表面增大了70.0%,下面层下表面增大了80.8%。,
3.1.3 速度对剪应力的影响由于不同车速下路面剪应力时程曲线图的形状基本类似,只是幅值不同,因此只选取车速为80 km/h时的沥青路面剪应力时程曲线图作为代表,见图 8。
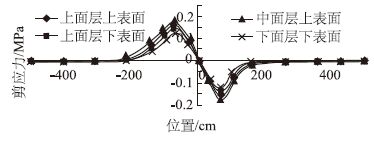
|
| 图 8 车速为80 km/h时沥青面层的剪应力时程曲线图 Fig. 8 Time history curves of shear stress in asphalt surface course at vehicle speed of 80 km/h |
|
|
在移动荷载作用下,沥青路面结构的面层都经历了方向相反的两次剪应力作用。从数值上看,剪应力在中面层上表面达到最大值,随后随着深度的增加剪应力值逐渐减小,由此可见提高上中面层接触区及中面层的抗剪切强度及抗剪切疲劳能力尤为重要。对不同速度下的最大剪应力进行汇总,为了能够更加直观反映不同车速下的最大剪应力变化规律,以曲线图形式表示,见图 9。
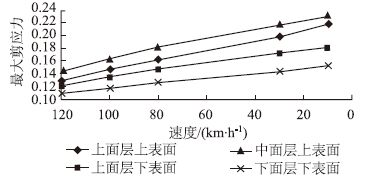
|
| 图 9 最大剪应力随车速变化曲线图 Fig. 9 Curves of maximum shear stress vs.vehicle speed |
|
|
由图 9可知,同一车速下,剪应力在中面层出现最大值,然后随着深度的增加而减小。在移动荷载作用下,最大剪应力随着车速的减小逐渐增大,并且基本呈现线性增大的趋势。从数值上看,当速度由120 km/h减小到10 km/h时,上面层上表面最大剪应力增大了69.8%,上面层下表面增大了50.4%,中面层上表面增大了60.4%,下面层下表面增大了40.4%。
3.2 制动刹车时的结构动力响应前文分析匀速状态下,车辆以不同速度下路面结构的动力响应;本节主要研究车辆减速运行过程,采用车辆刹车状态时产生的制动力模拟最不利(最大)路面水平力。水平力系数取0.6,大小为0.42 MPa。通过子程序施加水平力并实现速度的变化,令速度由80 km/h逐渐减小到0 km/h。
(1)对比图 4与图 10(a),制动刹车时与匀速行驶状态下垂直正应力的变化规律基本一致,只是幅值变大,这是因为车辆荷载移动到计算点正上方时其速度与制动刹车前的速度相比是减小的,这正符合速度对路面垂直正应力的结构响应规律,也说明水平力对路面结构的垂直正应力时程变化影响较小。

|
| 图 10 制动刹车时沥青面层曲线图 Fig. 10 Curves of asphalt surface course when braking |
|
|
(2)对比图 5与图 10(b),水平力的施加明显改变了沥青路面结构内部水平正应力的时程变化,车辆经过前后水平正应力产生了明显的突变;在沥青面层出现了较大的拉应力。从数值上看,与常规行驶状态下相比,以中面层上表面应力为例,增加水平力状况下路面所受的水平拉应力增大了890%,水平压应力增大了35.6%。由此可见:水平力对沥青路面受力状态有显著影响。
(3)对比图 6与图 10(c),与匀速行驶状态下路面结构内部剪应力时程变化规律比较,增加水平力状况下出现明显的不同。沥青面层不再承受正反剪应力两次作用,同时最大剪应力出现的位置也由常规行驶状态下的沥青中面层转移到沥青面层的上表面,此后随深度的增加其值在不断减小,从数值上看,增加水平力状况下,最大剪应力比常规行驶状态下增大了243%。可见,对于制动刹车频繁的路段尤其要加强上面层及上中面层接触面的抗剪能力。
4 结论通过计算分析可得出如下结论:
(1)在移动荷载作用下,半刚性基层沥青路面的面层主要处于三向受压状态,并且容易出现疲劳破坏。其中最大竖向压应力出现在上面层,最大水平压应力和最大剪应力出现在中面层。因此在路面铺筑时,一定要注意中上面层的压实质量和抗剪切强度,并充分考虑材料的抗疲劳性能。,
(2)在移动荷载作用下,较低的车速会使路面结构产生较大的应力,不同车速下路面结构的最大垂直压应力、最大水平压应力、最大剪应力随车速的减小而相应增大,并且基本呈现线性变化。因此车辆低速行驶路段比较容易产生车辙、拥包等病害。
(3)制动刹车时,水平力的施加对路面结构垂直正应力时程变化影响较小,对水平正应力和剪应力时程变化影响较大,明显改变了沥青路面结构内部水平正应力的时程变化,车辆经过前后水平正应力产生了明显的突变。沥青面层不再承受正反两次剪应力作用,同时剪应力最大值出现位置由常规行驶状态下的中面层变为上面层上表面。因此,在路面施工的时候,对于经常出现制动刹车的路段,一定要加强上、中面层的抗剪强度,尤其是上面层。
| [1] | 马新,郭忠印,杨群.移动荷载作用下沥青路面动态响应三维有限元分析[J].重庆大学学报:自然科学版,2009,28(4):702-707.MA Xin,GUO Zhong-yin,YANG Qun. 3D Finite Element Analysis on Asphalt Pavement Dynamic Response under Moving Load [J]. Journal of Chongqing University: Natural Science Edition, 2009, 28(4):702-707. |
| [2] | 冯俊领.交叉口沥青路面剪切损害机理及剪切试验方法研究[D]. 上海:同济大学,2007.FENG Jun-ling. Study of Shear Damage Mechanism and Test Method of Asphalt Pavement at Intersection[D]. Shanghai: Tongji University, 2007. |
| [3] | 倪富健,王燕芳,马翔.城市道路交叉口沥青路面受力分析[J].公路交通科技,2010,27(7):41-45.NI Fu-jian, WANG Yan-fang, MA Xiang. Mechanical Analysis of Asphalt Pavement in Urban Intersections[J]. Journal of Highway and Transportation Research and Development, 2010, 27(7): 41-45. |
| [4] | 李立新,丁学峰,李跃军.移动荷载作用下长大纵坡沥青路面力学响应分析[J].公路工程,2009,34(6):38-42,46.LI Li-xin,DING Xue-feng,LI Yue-jun. Research on Mechanical Response of Asphalt Pavement with Moving Load on Long and Steep Longitudinal Slope[J]. Highway Engineering,2009,34(6):38-42,46. |
| [5] | 单景松,黄晓明,廖公云.移动荷载下路面结构应力响应分析[J]. 公路交通科技,2007,24(1):10-13.SHAN Jing-song, HUANG Xiao-ming, LIAO Gong-yun. Dynamic Response Analysis of Pavement Structure under Moving Load[J]. Journal of Highway and Transportation Research and Development, 2007, 24(1):10-13. |
| [6] | 王保实.移动荷载作用下半刚性基层沥青路面结构的动力响应研究[D].西安:西安建筑科技大学,2011.WANG Bao-shi. Study of Dynamic Response of Semi-rigid Base Asphalt Pavement under Moving Load[D]. Xi'an:Xi'an University of Architecture and Technology,2011. |
| [7] | 邓学钧,黄晓明,沈伟新.弹性层状体系的动力响应分析[J].土木工程学报,1995,28(3):9-16.DENG Xue-jun, HUANG Xiao-ming, SHEN Wei-xin. Dynamic Response Analysis of Elastic Muti-layered System[J].China Civil Engineering Journal, 1995, 28(3): 9-16. |
| [8] | 马宏伟,吴斌.弹性动力学及其数值方法[M].北京:中国建材工业出版社,2000.MA Hong-wei, WU Bin. Elastic Dynamics and Numerical Method[M]. Beijing: China Building Materials Industry Press, 2000. |
| [9] | 王金昌,陈页开.ABAQUS在土木工程中的应用[M].杭州:浙江大学出版社,2006.WANG Jin-chang, CHEN Ye-kai. Application of ABAQUS in Civil Engineering[M]. Hangzhou: Zhejiang University Press, 2006. |
| [10] | 郑健龙,吕松涛,田小革.沥青混合料粘弹性参数及其应用[J].郑州大学学报:工学报,2004,25(4):8-11,15.ZHENG Jian-long,L Song-tao,TIAN Xiao-ge. Research on Viscoelastic Parameters of Bituminous Mixtures and Their Applications [J]. Journal of Zhengzhou University: Engineering Science Edition, 2004, 25(4):8-11, 15. |
| [11] | 郑健龙,钱国平,应荣华.沥青混合料热粘弹性本构关系试验测定及其力学应用[J].工程力学,2008,25(1): 34-41.ZHENG Jian-long, QIAN Guo-ping, YING Rong-hua. Testing Thermalviscoelastic Constitutive Relation of Asphalt Mixtures and ITS Mechanical Application[J]. Engineering Mechanics, 2008, 25(1): 34-41. |
| [12] | 杨博.基于有限元方法的沥青路面车辙影响因素分析及其应用研究[D].西安:长安大学,2010.YANG Bo. Influencing Factors of Asphalt Pavement Rutting and Applications Based on Finite Element Method[D]. Xi'an:Chang'an University,2010. |
| [13] | 程小亮.基于非线性蠕变方程沥青混合料永久变形特性研究[D].哈尔滨:哈尔滨工业大学,2010.CHENG Xiao-liang. Study on Permanent Deformation of Asphalt Mixture Based on Nonlinear Creep Equation[D]. Harbin:Harbin Institute of Technology,2010. |
| [14] | 贾璐.沥青路面温度场预估方法及其应用[D].上海:同济大学,2008.JIA Lu. Prediction Method and Application of Temperature Field in Asphalt Pavement[D].Shanghai:Tongji University,2008. |
 2015, Vol. 31
2015, Vol. 31