扩展功能
文章信息
- 杜春燕, 马洪伟, 周溪召
- DU Chun-yan, MA Hong-wei, ZHOU Xi-zhao
- 基于Edgeworth级数的行程时间可靠性的计算与实证
- Calculation and Empirical Analysis of Travel Time Reliability Based on Edgeworth Series
- 公路交通科技, 2015, Vol. 31 (7): 127-133
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (7): 127-133
- 10.3969/j.issn.1002-0268.2015.07.020
-
文章历史
- 收稿日期:2014-8-27
2. 上海电机学院 商学院, 上海 201306
2. School of Business, Shanghai Dianji University, Shanghai 201306, China
随着生活节奏的加快,用户对出行质量的要求越来越高,交通网络可靠性方面的研究日益成为热点,致力于使出行者安全、舒适、方便、快捷地到达目的地。行程时间可靠性是研究交通网络可靠性的重要指标之一,被定义为车辆在规定的时间内完成起讫点出行的概率。在用户的出行选择中,行程时间往往是关注的焦点,用户希望在期望的行程时间内尽可能快地到达终点,同时交通规划与管理部门也希望能减小行程时间波动的幅度以提供更稳定的服务。因此,科学计算的路段行程时间可靠性是衡量路网性能的重要手段,也为建设合理、可靠的道路交通网络系统提供有力支持。本文利用Edgeworth级数研究行程时间可靠性可以进一步完善交通网络可靠性的理论,具有重要的现实意义和广阔的应用前景。
1 研究概述Asakura和Kashiwadani[1]于1991年首次提出了行程时间可靠性的概念,即规定的时间内车辆从起点到达终点的概率,并假设行程时间服从正态分布。DEVI V L[2]研究了基于流量守恒法的模型,以通行能力、流量、自由流速度为自变量来估计平均行程时间。Abdel-Aty[3]发现人们不但关注行程时间,而且关心行程时间的随机波动,大约54%的被访者认为行程时间可靠性是他们作出路径选择决策的首要或次要因素。Srinivas Peeta[4]等人提出自适应信息融合模型,即在各个离散时间点反复将可获得的过去与实时的路段行程时间的信息结合起来考虑,从而预测短期内的路段行程时间的分布,指出有代表性的短期行程时间分布均值并不一定是一个好的实时行程时间分布的跟踪指标。Huizhao Tu[5]等人利用基于风险评估技术的解析公式来计算由所有交通故障后果和相应的故障概率组成的行驶时间不可靠的成本,以评论路网的性能。Michael A P Taylor[6]等人认为博尔分布形状更为灵活,因而能更好地反映行程时间的变化,提出用博尔分布来拟合行程时间可靠性模型。ManWo Ng[7]等人构建了行程时间可靠性的自由分布,该分布涵盖了所有给路网行程时间带来不确定性因素的来源,通过半解析概率不等式快速计算出所需的概率上界以取代传统的通过密集型计算获得行程时间超过一定阈值的精确概率。
近年来,国内学者也对行程时间可靠性方面的问题进行了广泛而深入的研究,并取得了一定的成果。裴玉龙[8]等研究了公路网的行程时间可靠度,但是忽略了网络的可达性和覆盖率要求。郭寒英[9]等分析了突发事件下路网的行程时间可靠性,对交通流量和出行时间之间的关联进行了讨论,通过实证得出了突发事件发生时路网行程时间可靠性与其交通流量有直接关系的结论。高自友[10]等通过分析交通网络设计的双层规划模型,提出了与土地利用相结合的连续平衡交通网络设计、基于PUE的交通连续平衡网络设计以及基于环境污染限制和最优信号控制的交通连续平衡网络设计等方法,但均未考虑交通网络的随机性。张勇[11]等按照频数频率统计方法,通过对连续若干天的历史行程时间数据分析,结果显示在有信号控制的主干道,行程时间不符合正态分布。同时实证表明行程时间分布存在偏峰和时滞现象,最后分析了行程时间分布中的可靠系数、峰度统计参量与行程时间可靠度的变化关系。陈琨[12]等研究了路段行程时间服从对数正态分布时,如何计算路径行程时间可靠性的问题,根据对数正态随机变量之和的概率分布特性,建立了路径行程时间可靠性评价模型。侯立文[13]为了反映行程时间的尖峰厚尾特征,设计了一种栅格行程时间预测方法,引入了可以反映更多行程时间信息的Gram-Charlier分布函数,仿真验证该方法的有效性。
综上所述,现阶段国内外许多学者通过拟合行程时间分布函数,规定行程时间阈值,建立可靠度模型,研究了路网的行程时间可靠性。对于行程时间的分布仍然没有定论:有正态函数、对数正态函数、Burr分布等多种类型,分布规律有待深入研究。上述函数适用范围小,且迁移性不高,对于特定路段交通流量引起的行程时间波动不够敏感,而Edgeworth级数在某些情况下可以逼近这些分布,并且能够突出行程时间的偏态特征,具有更强的适应性。因此,本文基于实际的路段行程时间数据,探讨几个典型时刻的路段行程时间的分布规律,对于那些不规则的行程时间分布,选用Edgeworth级数来进行逼近其分布函数,进而计算路网行程时间的可靠性。
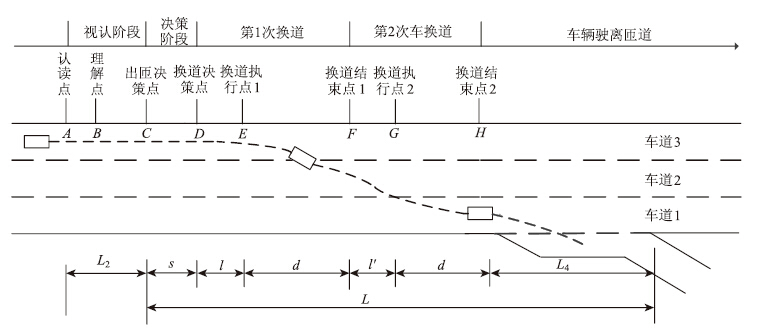
2 路段行程时间可靠性分析行程时间是交通工程的一项基本指标。一般来说,区域越大出行时间也越长;对于同等规模的城市出行时间耗越少,说明城市交通系统规划越合理。行程时间可靠性主要用来描述交通出行在规定的时间内完成的可能性,除了与道路上的交通状况密切相关之外,还和很多因素有关,比如道路通行能力、交通流量、信号灯周期等。当路段长度、交通量、车辆加速度以及信号配时获知的前提下,出行者由起点O到终点D,行程时间不超过T的可靠性为R(t),由可靠性的定义可得:
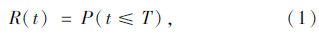
|
| 图 1 行程时间可靠性直观图 Fig. 1Pictorial diagram of travel time reliability |
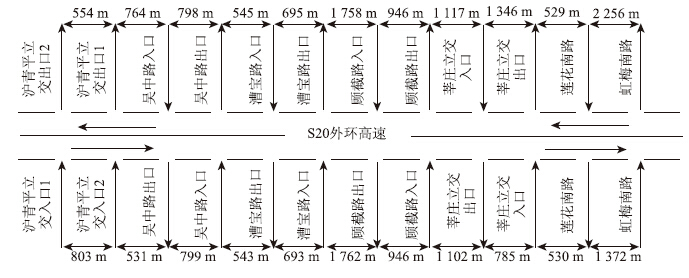
本文研究路段为上海外环发布段,图 2为沪青平立交与虹梅南路之间的S20外环高速示意图,获得了该研究区段各个路段2013年5月1日—7月31日期间,每天每间隔2 min的车流量和车辆行驶瞬时速度,根据速度位移关系,得到相应的路段行程时间,并分析其分布特征。
|
| 图 2 外环分布段示意图 Fig. 2Schematic diagram of outer ring section distribution |
本文根据路段流量特征,大致分析了路段几个典型时段(表 1)的行程时间分布情况,发现路段行程时间存在服从正态分布和对数正态分布的现象,但大部分用正态分布和对数正态分布来拟合的准确度均不高。
| 研究时段 | 3:00—4:00 | 8:00—9:00 | 10:00—11:00 | 12:00—13:00 |
| 峰期 | 自由流时段 | 早高峰 | 平峰时段 | 午高峰 |
| 研究时段 | 15:30—14:30 | 17:30—18:30 | 20:30—21:30 | |
| 峰期 | 平峰时段 | 晚高峰 | 平峰时段 |
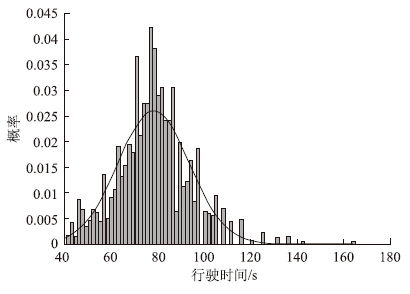
对漕宝路—顾戴路路段早高峰8:00的行程时间数据拟合正态分布并进行K-S检验,通过MatLab绘制相应的直方图与正态分布概率密度图(图 3),并得到相应的P值0.109 9,大于显著性水平0.05,则认为该路段的行程时间服从正态分布。
|
| 图 3 行程时间拟合正态分布 Fig. 3Normal distribution fitting of travel time |
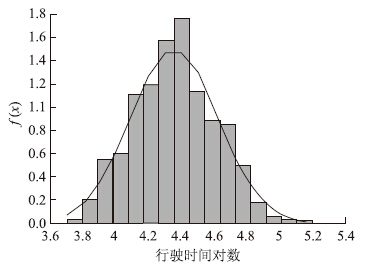
对顾戴路—漕宝路路段10:00行程时间数据求对数,并将相应的对数结果进行正态分布拟合,见图 4,通过K-S检验,得到其P值等于0.067 6,大于0.05,认为该路段的行程时间服从对数正态分布。
|
| 图 4 行程时间拟合对数正态分布 Fig. 4Logarithm normal distribution fitting of travel time |
虽然有些路段某个时间窗的行程时间服从正态分布或者对数正态分布,但实际上大城市的交通状况早已使行程时间变得难以确定,行程时间规律越来越不明显,使得行程时间分布函数和密度函数很难显式地表达出来,在这种情况下,可以利用其他的近似表达式来计算行程时间可靠性。
常用的渐近展开表达方式,有Gram-Charlier级数、Edgeworth级数等。Gram-Charlier级数和Edgeworth级数的主要思想是把待逼近分布函数或密度函数的特征方程,写成另一个已知分布(常见的作法是选用正态分配作为已知分布,但事实上选用其他的函数也是可行的)特征方程的展式,再经过Fourier变换的逆变换,就可以求得分布函数的展开式,详细证明过程可以参考文献[14,15,16]。
利用概率密度函数的Edgeworth展开式。若随机变量行程时间为t,μ为其均值,σ2为方差,令y=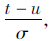 则y的概率密度函数可以展成以下级数:
则y的概率密度函数可以展成以下级数:
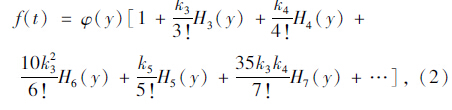
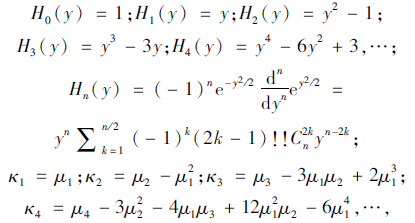
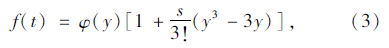
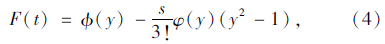
根据式(1)、式(4),行程时间可靠性最终可以简化为:
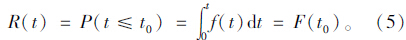
部分学者认为高峰时段行程时间服从正态分布,非高峰时间段的行程时间则服从对数正态分布[17]。在本文的实证分析过程中也发现,通过正态分布检验和对数正态分布检验的分别是高峰时刻和非高峰时刻,因此,在本节中,选择用Edgeworth级数拟合高峰时刻路段行程时间分布,并与相应的正态分布情形对比分析。
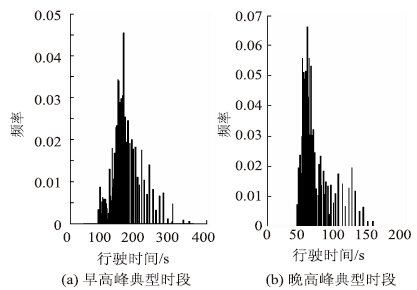
图 5给出了顾戴路—漕宝路匝道路段2013年5月1日至7月31日早晚高峰典型时刻(8:00、17:30)的行程时间概率分布(请注意坐标刻度)。这两个时刻的交通流量逐渐接近或已经处于饱和状态,行程时间的波动幅度较大,均为非对称分布,相比于正态分布而言,存在一定的偏度。用s1和s2分别表示两者的偏度,通过计算,s1=1.07,s2=1.93,表明早晚高峰时刻的行程时间峰值向左偏。并且,即便是同一路段早晚高峰不同时刻行程时间的变化趋势、波动幅度以及行程时间的众数也存在差别,关于行程时间的研究应注意其动态变化特征。
|
| 图 5 早晚高峰典型时段行程时间概率分布图 Fig. 5Probability distributions of morning and evening rush hours typical travel time |
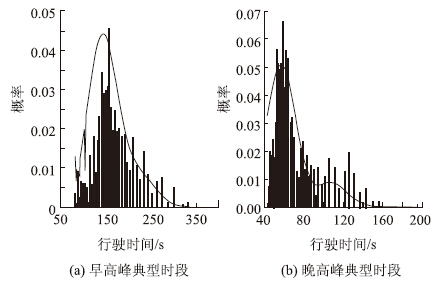
图 6为早晚高峰典型时刻Edgeworth级数行程时间概率密度函数与直方图比对图,可见,Edgeworth级数行程时间概率密度函数基本能够反映行程时间的变化趋势。将Edgeworth级数行程时间估计与正态分布做比较,早高峰时刻相关数据列于表 2。通过计算正态分布的期望概率、Edgeworth级数行程时间的期望概率与实际频率之间的绝对误差来比较二者估计行程时间的准确度,文中用最大绝对误差值、平均绝对误差以及误差平方和这3个参数来描述,结果见表 3,相应的晚高峰时刻的分析结果见表 4。可以看出,用Edgeworth级数估算出来的行程时间的最大绝对误差值、平均绝对误差与误差平方和均小于正态分布,Edgeworth级数估计值与实际频率之间的误差较小。现阶段,大部分行程时间可靠性计算模型均假设道路行程时间服从正态分布,验证结果也表明正态分布满足精度要求,而用Edgeworth级数拟合的行程时间分布准确度显然高于正态分布,因此,本文提出的基于Edgeworth级数的行程时间分布模型具有可行性。
|
| 图 6 Edgeworth级数行程时间概率密度函数与直方图对照图 Fig. 6Contrast of Edgeworth series travel time probability density function and histogram |
| 编号 | 分组 | 频数 | 频率 |
正态分布 期望概率 |
Edgeworth分布 期望概率 |
| 1 | (80,90] | 2 033 | 0.025 2 | 0.018 7 | 0.017 1 |
| 2 | (90,100] | 2 622 | 0.032 5 | 0.028 1 | 0.032 3 |
| 3 | (100,110] | 2 261 | 0.028 0 | 0.039 8 | 0.051 3 |
| 4 | (110,120] | 3 135 | 0.038 9 | 0.053 2 | 0.071 8 |
| 5 | (120,130] | 5 437 | 0.067 4 | 0.067 1 | 0.090 0 |
| 6 | (130,140] | 8 004 | 0.099 3 | 0.079 9 | 0.102 5 |
| 7 | (140,150] | 12 342 | 0.153 0 | 0.089 8 | 0.106 4 |
| 8 | (150,160] | 13 396 | 0.166 1 | 0.095 2 | 0.101 5 |
| 9 | (160,170] | 5 685 | 0.070 5 | 0.095 3 | 0.089 5 |
| 10 | (170,180] | 5 538 | 0.068 7 | 0.090 1 | 0.073 8 |
| 11 | (180,190] | 4 819 | 0.059 8 | 0.080 3 | 0.057 9 |
| 12 | (190,200] | 3 721 | 0.046 1 | 0.067 6 | 0.044 5 |
| 13 | (200,210] | 1 178 | 0.014 6 | 0.053 7 | 0.034 9 |
| 14 | (210,220] | 3 543 | 0.043 9 | 0.040 2 | 0.028 4 |
| 15 | (220,230] | 900 | 0.011 2 | 0.028 5 | 0.024 0 |
| 16 | (230,240] | 1 792 | 0.022 2 | 0.019 0 | 0.020 4 |
| 17 | (240,250] | 1 047 | 0.013 0 | 0.012 0 | 0.016 9 |
| 18 | (250,260] | 408 | 0.005 1 | 0.007 1 | 0.013 5 |
| 19 | (260,270] | 843 | 0.010 5 | 0.004 0 | 0.009 9 |
| 20 | (270,280] | 929 | 0.011 5 | 0.002 1 | 0.007 0 |
| 21 | (280,290] | 156 | 0.001 9 | 0.001 1 | 0.004 3 |
| 22>290 | 852 | 0.010 6 | 0.000 0 | 0.005 6 |
| 类别 | 正态分布 | Edgeworth级数分布 |
| 最大绝对误差值 | 0.070 9 | 0.064 6 |
| 平均绝对误差 | 0.016 9 | 0.013 8 |
| 误差平方和 | 0.013 8 | 0.009 9 |
| 类别 | 正态分布 | Edgeworth级数分布 |
| 最大绝对误差值 | 0.261 5 | 0.184 0 |
| 平均绝对误差 | 0.047 5 | 0.031 3 |
| 误差平方和 | 0.090 6 | 0.043 8 |
本文选择上海外环内侧吴中路上匝道至沪青平立交出口匝道和外环外侧沪青平立交入口匝道2至吴中路出匝道之间的路段为实例进行分析,这两个路段的长度分别为763,531 m。利用上海城市交通信息中心提供的原始数据,统计出2013年7月1日至7月31日晚高峰时刻17:30经过这两个路段每2 min间隔每一辆车的实际行程时间。tf取该时刻行程时间分布的中位行程时间,即65 s和49 s,假设r=1.2。
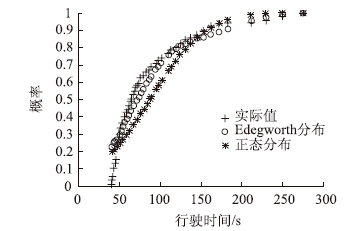
根据式(4)可以获得研究区段的行程时间分布,从图 7、图 8可以看出,Edgeworth分布围绕着实际值变化,偏离幅度总体较小,明显优于正态分布。与此相应,在式(4)基础上求得的行程时间可靠性的误差也明显小于正态分布,见表 5。
|
| 图 7 吴中路至沪青平公路行程时间分布 Fig. 7Travel time distribution of Wuzhong Road to Huqingping Road |

|
| 图 8 沪青平公路至吴中路行程时间分布 Fig. 8Travel time distribution of Huqingping Road to Wuzhong Road |
| 路段 | 指标 | 实际值 | Edgeworth级数分布 | 正态分布 |
| 吴中路至沪青平 | 可靠性 | 0.627 | 0.548 | 0.434 |
| 误差 | 0 | 0.079 | 0.193 | |
| 沪青平至吴中路 | 可靠性 | 0.674 | 0.712 | 0.603 |
| 误差 | 0 | 0.038 | 0.071 |
由于我国目前尚未制订规定行程时间可靠性阈值的标准,故参考Nota Mobility(AVV,2004)(荷兰国家交通政策文件)[18]中的可靠性目标设定评判阈值,该目标表示为:R(t)=P(t≤T≥90%)。但荷兰每天骑车出行人数约达5万,适龄骑车者人均拥有1.3辆自行车[19],道路上自行车占有绝对路权,而中国城市的骑车出行率并不高,道路交通构成与荷兰存在较大差异,且荷兰城市的人口基数远低于中国,所以直接套用荷兰目标显然不合中国国情,因此将我国行程时间可靠性阈值设为80%。本案中的行程时间可靠度分别为0.548和0.712,均低于0.8。由式(1)可知,可以通过增大T或减小t以达到提高R(t)的目的,增大T即提高人们的容忍度来提升路段的行程时间可靠度,这显然是不合理的,也不能反映道路服务性能的提升。速度是影响行程时间t的关键因素,而影响行车速度的主要因子包括道路通行能力、车流量、绿信比等[20],所以通过改善交通组织和道路硬件设施能够提高道路行程时间的可靠性。
5 结论行程时间的概率分布和可靠度一直是交通出行研究的热点问题,本文在探讨路段行程时间分布规律性的过程中,利用Edgeworth级数来近似行程时间分布函数,取得了较好的效果。当然,本文的工作还可以进一步得到加强:一方面,Edgeworth级数估计的行程时间可靠性的精度有待进一步提升,应将其在更大规模的路网上进行试验,以获得更为准确的参数估计值;另一方面,本文的行程时间可靠性计算方法主要适用于评价,动态的、用来预测未来时间段的行驶时间可靠性模型还有待深入研究。
| [1] | ASAKURA Y,KASHIWADANI M. Road Network Reliability Caused by Daily Fluctuation of Traffic Flow in [C]// Proceedings of the 19th PTRC Summer Annual Meeting. Brighton:[s.n.].1991:73-84. |
| [2] | DEVI V L. Estimation and Prediction of Travel Time From Loop Detector Data for Intelligent Transportation Systems Applications[D]. College Station:Texas A&M University,2004. |
| [3] | ABDEL-ATY M A,KITAMURA R,JOVANIS P P. Investigating Effect of Travel Time Variability on Route Choice Using Repeated-measurement Stated Preference Date[J]. Transportation Research Record,1995,1493:39-45. |
| [4] | DU Li-li,PEETA S, KIM Y H. An Adaptive Information Fusion Model to Predict the Short-term Link Travel Time Distribution in Dynamic Traffic Networks[J]. Transportation Research Part B,2012,46(1):235-252. |
| [5] | TU Hui-zhao,LI Hao, VAN ZUYLEN H,et al. Modeling Travel Time Reliability of Freeways Using Risk Assessment Techniques[J]. Transportation Research Part A,2012,46(10):1528-1540. |
| [6] | TAYLOR M A P. Modeling Travel Time Reliability with the Burr Distribution [J]. Procedia-social and Behavioral Sciences, 2012,54:75-83. |
| [7] | NG M W,SZETO W Y,WALLER S T. Distribution-free Travel Reliability Assessment with Probability Inequalities[J]. Transportation Research Part B,2011,45(6):852-866. |
| [8] | 裴玉龙,益春英.公路网络运营可靠度研究[J].公路交通科技,2005,22(5):119-123. PEI Yu-long,YI Chun-ying. Study on Operation Reliability of Highway Network[J]. Journal of Highway and Transportation Research and Development,2005,22(5):119-123. |
| [9] | 郭寒英,石红国.突发事件下路网运行时间可靠性研究[J].公路交通科技,2005,22(8):102-105. GUO Han-ying,SHI Hong-guo. Study on Network Travel Time Reliability under Contigent Events[J]. Journal of Highway and Transportation Research and Development,2005,22(8):102-105. |
| [10] | 宋一凡,高自友. 连续平衡网络设计问题的双层规划模型及其求解算法[J]. 公路交通科技,1999,16(1):42-45. SONG Yi-fan,GAO Zi-you. A Bilevel Programming Model and Solution Algorithm for the Continuous Equilibrium Network Design Problem[J]. Journal of Highway and Transportation Research and Development,1999,16(1):42-45. |
| [11] | 张勇,王世光,杨晓光.信号控制道路行程时间可靠度计算与实证[J].同济大学学报:自然科学版,2009,37(6):772-776. ZHANG Yong,WANG Shi-guang,YANG Xiao-guang. Computing and Demonstration of Travel Time Reliability on Signalized Road[J]. Journal of Tongji University:Natrual Science Edition,2009,37(6):772-776. |
| [12] | 陈琨,于雷.基于对数正态和分布的路径行程时间可靠性模型[J].北京交通大学学报,2009,33(3):35-39. CHEN Kun,YU Lei. Route Travel Time Reliability Model Based on Lognormal Sum Distribution[J]. Journal of Beijing Jiaotong University,2009,33(3):35-39. |
| [13] | 侯立文,谭家美.城市交通中利用Gram-Charlier分布估计行程时间可靠性[J].中国管理科学,2009,17(6):139-146. HOU Li-wen,TAN Jia-mei. Estimating Travel Time Reliability in Urban Transportation Using Gram-charlier Distribution [J]. Chinese Journal of Management Science,2009,17(6):139-146. |
| [14] | CRAMER H. On the History of Certain Expansions used in Mathematical Statistics[J]. Biomerika, 1972,59(1):205-207. |
| [15] | FELLER W. An Introduction to Probability Theory and Its Applications[M]. New York:John Wiley,1966. |
| [16] | KENDALL M G,STUART A. The Advanced Theory of Statistics [M]. London:Charles Griffin,1977. |
| [17] | 况爱武,黄中祥,况群. 随机需求道路网络出行时间可靠性评估方法[J].西南交通大学学报,2011,46(5):861-867. KUANG Ai-wu,HUANG Zhong-xiang,KUANG Qun. Evaluation Method for Travel Time Reliability of Road Network with Stochastic Demand[J]. Journal of Southwest Jiaotong University,2011,46(5):861-867. |
| [18] | AVV Transportation Research Centre,Dutch Ministry of Transport,Public Works and Water Management. Nota Mobility[EB/OL]. [2007-04-26]. http://international.fhwa.dot.gov/pubs/pl07002/vsw_eu07.pdf. |
| [19] | LI Z,HENSHER D A, ROSE J M. Willingness to Pay for Travel Time Reliability in Passenger Transport:A Review and Some New Empirical Evidence [J]. Transportation Research E,2010,46(3):384-403. |
| [20] | 冷军强,张亚平,赵兴奎,等.基于广义出行费用的城市路网行程时间可靠性[J]. 公路交通科技,2010,27(7):133-137. LENG Jun-qiang,ZHANG Ya-ping,ZHAO Xing-kui,et al. Travel Time Reliability of Urban Road Network Based on Generalized Travel Cost[J]. Journal of Highway and Transportation Research and Development,2010,27(7):133-137. |
 2015, Vol. 31
2015, Vol. 31
