扩展功能
文章信息
- 李颖宏, 郑增强, 郭伟伟, 张星愿
- LI Ying-hong, ZHENG Zeng-qiang, GUO Wei-wei, ZHANG Xing-yuan
- 交叉口直行待行区设置研究
- Research on Setting of Waiting Area for Through Vehicles at Intersection
- 公路交通科技, 2015, Vol. 31 (7): 120-126
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (7): 120-126
- 10.3969/j.issn.1002-0268.2015.07.019
-
文章历史
- 收稿日期:2015-4-27
城市道路信号交叉口是城市道路的重要节点,在有限的空间里,不同方向的交通流在此汇集,使交叉口的交通组织错综复杂,是影响道路通行效率的重要环节[1,2]。而待行区的设置是缓解交叉口拥堵的有力措施之一,基于待行区的诸多研究,如尚德申主要研究待行区设置方法和以及设置最佳的待行区长度,通过实例表明,合理设置直行待行区可以提高进口车道的利用率,减少延误[3];左天福分析直行待行区的适用条件和设置方法,并依据典型路口仿真论证,合理设置待行区可以缩短周期时长,减少延误,提高车道的资源利用率[4];李小帅研究待行区的设计条件和通行能力计算方法,并通过实例验证,设置左转和直行待行区后,提高通行能力,降低延误,优化效果显著[5]。但是学者们的研究尚未深入探究待行区设置前后信号控制参数的变化,以及通行能力和延误模型的异同。本文建立设有待行区的直行车道通行能力和延误模型,结合交叉口几何尺寸,详细分析信号控制参数的变化,最后通过实例验证模型的正确性,表明在一定条件下待行区能提高直行车道的通行能力,降低车均延误,但并不是所有的情况下都适合设置待行区。
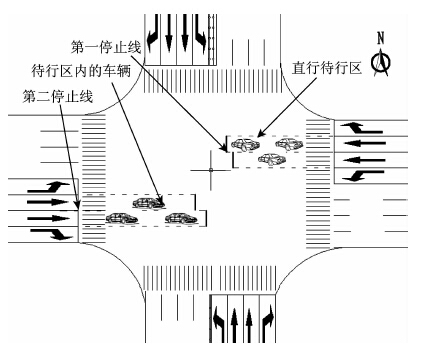
1 直行待行区设置直行待行区是指交叉口进口道的某一条或几条直行车道前划出一块空间区域,并标有平行的白色虚线边框。这种设计允许直行车辆在上一相位绿灯放行时进入待行区,当直行相位绿灯结束后,不允许直行车辆进入待行区。待行区可以通过延伸直行车道的长度,使停止线深入到交叉口中央,充分利用交叉口内部的空间资源。当直行车辆在直行相位的红灯期间提前进入待行区进行等待,达到了最大限度地利用时间换取空间;当直行相位的信号灯变为绿灯时,在待行区的车辆开始启动通过交叉口,此时又最大限度地利用空间换取时间,最终达到时间和空间相互转换的目的[6],直行待行区示意图如图 1所示。
|
| 图 1 直行待行区示意图 Fig. 1Schematic diagram of waiting area for through vehicles |
冲突相位的车辆行驶轨迹是直行待行区长度设置的基础,其中容纳的机动车数量是待行区是否设置的依据。待行区停止线可以在同一直线上,也可以根据交叉口的实际情况设成阶梯状,但不能影响其他方向的车辆通行。
待行区的设置分为2类:一类是主干道和主干道交叉口情况,冲突相位方向的绿灯时间相差不大,根据路口的几何条件设置待行区,充分利用交叉口的空间区域,提高车道的通行能力;另一类在主干道和次干道且主次干道绿灯时长相差较大,优先在次干道设置待行区,原因是当交叉口是主次干道相交时,次干道方向的路口空间区域较大,把待行区设置在次干道可以充分利用路口中央的空间区域,达到充分利用路口的空间区域和有限的绿灯时间的目的,提高车道的通行能力,减少延误。待行区的设置应具备以下几个条件[7,8]:
(1)路交叉口是主干道与主干道或主次干道,以保证有足够的车道数和直行待转区长度;
(2)设置直行待行区的进口必须有专用的左转车道;
(3)进口道直行车辆多,且相邻交叉口具有相应的消散能力,防止拖尾与待行形成道路阻塞。
2 通行能力和延误模型建立道路交叉口整体交通状态通过评价指标来体现,如交叉口的通行能力、延误、排队长度、停车次数等等,而交叉口最重要的目的是最大限度地提高通行能力,减少延误,故本文主要通过建立有待行区的直行车道的通行能力和延误模型,达到在有限的空间区域内,最大限度提高交叉口的通行能力和较少延误时间的目的。假设以下条件[9,10]:
(1)直行车辆以均匀的随机到达率到达交叉口,直行车辆的到达率不影响其消散率;
(2)设置直行待行区的进口道上游有足够的消散能力,不能与待行区进口道形成阻塞;
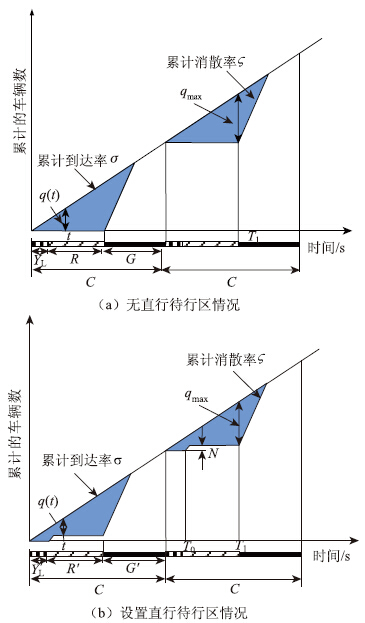
2.1 通行能力模型图 2是信号控制交叉口在有无待行区情况下直行车辆的到达和消散的说明图。曲线的斜率分别代表 2种状态下直行车辆的到达率和消散率。 YL,R,G分别代表无直行待行区时黄灯、红灯和绿灯时长,Y′L,R′,G′分别代表有直行待行区时黄灯、红灯和绿灯时长,黑色区域代表单个周期内第二停止线之后累计的排队车辆数,q(t)代表t时刻的排队长度。图 2(a)显示无待行区时直行车辆在直行灯变黄后如果车头还没越过停止线的车辆就开始排队,一直延续到在本相位绿灯亮。由图 2(a)可知,每周期的直行绿灯开启时刻(T1时刻)达到最大值qmax,此后排队车辆开始消散,直到消散完毕为止。如图 2(b)所示,有待行区时在前一相位放行时,排在第二停止线后面的前N辆直行车进入待行区等待,第二停止线后面的排队长度在每周期的直行相位绿灯开启时(T1时刻)达到最大值q′max,故有待行区时整个排队车辆数等于停留在待行区的车辆数与停留在第二停止线后面的车辆数的总和。本文运用停止线法分析有无待行区通行能力的变化,首先考虑设置待行区前后信号控制参数的变化。
|
| 图 2 直行待行区前后对比分析图 Fig. 2Difference between an intersection with and without waiting area for through vehicles |
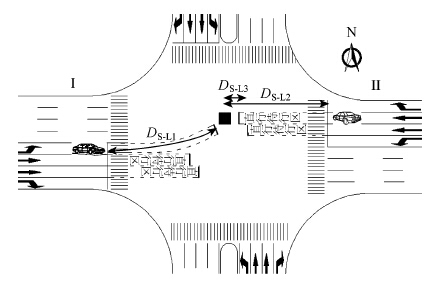
绿灯间隔时间是指一股交通流的绿灯结束时刻和下一股交通流的绿灯开始时刻的时间间隔,所需要的最短绿灯间隔时间tZ由通过时间tp、清空时间tr与进入时间te确定。进入时间分为2个阶段,加速阶段和匀速阶段,机动车从停止线启动进入交叉口达到一定的速度后,近似认为机动车匀速通过交叉口。由于直行待行区的设置,交叉口的放行次序是先左转后直行,直行车辆进入冲突点的距离缩短,在前一相位左转车清空距离不变的情况下绿灯间隔时间增加[11,12]。后一相位与直行相位的绿灯间隔时间与是否设置直行待行区无关,故本文不再讨论。如图 3所示交叉口几何尺寸图。
|
| 图 3 直行待行区设置的几何尺寸图 Fig. 3Geometric dimensions for setting waiting area for through vehicles |
假定交叉口交通状态如图 3所示,各参数含义如下:
DS-L1为I进口停止线至冲突区域边界的距离;
DS-L2为II进口未设置待行区时停止线至冲突边界的距离;
DS-L3为II进口道设置待行区后停止线至冲突边界的距离;
DL为标准车长;
a1为I进口车辆的加速度;
ε为I进口末车通过冲突点的时间;
v为车辆行驶速度;
vl为交叉口限速;
τ′1为未设置待行区时绿灯间隔时间;
τ″1为设置待行区时绿灯间隔时间;
τ′2为II进口道未设置待行区时由停止线至冲突区的时间;
τ″2为II进口道设置待行区时由停止线至冲突区的时间;
δ2为II进口驾驶员启动反应时间;
a+2为II进口车辆加速度;
R为全红时间。
图 3中的黑色方框是冲突区域,表示冲突车流运行轨迹交点为核心的一定区域,冲突车辆不能同时存在该区域内。
当黄灯开启时,I进口左转末车越过停止线,此时绿灯间隔时间要保证末车能安全通过冲突区。末车的速度为v,不同驾驶员开车的习惯不同,通过交叉口的速度也会有差异,在左转距离DS-L1中分别讨论车辆是否达到限速,下面分别讨论能安全通过冲突区需满足的前提条件。
假设左转相位的红灯启亮时,左转末车刚好以速度v越过停止线,其到达冲突区域时需要考虑是否达到限速,以下分别讨论这2种情况。
如果未达到限速,则左转末车通过冲突区的时间为:
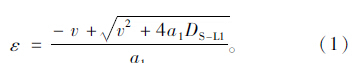
如果达到限速,则左转末车通过冲突区的时间为:
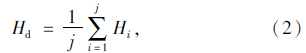
式(2)第一项为左转末车加速的时间,第二项为达到限速后匀速的时间。
II进口道直行车道待行区设置改变了头车到冲突区域的距离,致使绿灯间隔时间发生变化,故需要分别讨论设置待行区前后绿灯间隔时间的变化,以下分为未设置和设置待行区的情况:
(1)未设置待行区,II进口未设置待行区时停止线前第一辆车启动并加速行驶到冲突区域的时间是τ′2,车辆持续加速可能会达到限速,故τ′2存在2种可能。
未达到限速,直行车一直处于加速状态,此时通过冲突区域的时间为:
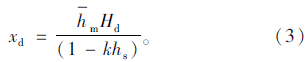
达到限速时,II进口道直行车先加速行驶直到限速,然后再以限速值匀速通过冲突区域,此时所用的时间为:
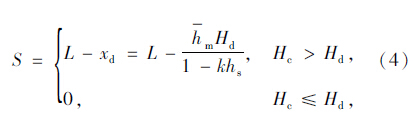
(2)设置待行区时,和未设置待行区有类似的情况,τ′2也存在2种可能。
若车辆未到冲突区域前已经达到限速,则需要满足:
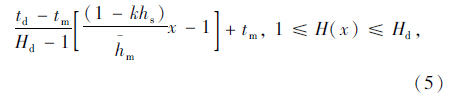
若车辆到达冲突区域还未达到限速,则须满足:
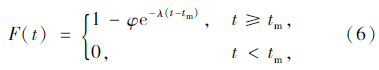
直行相位与前一相位的绿灯间隔时间为:
(1)无待行区时

(2)有待行区时
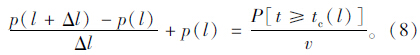
有效绿灯时间ge由绿灯显示时间减去车辆起动延误,再加上黄灯时间确定。车辆起动延误可以分为反应延误和非饱和延误2个部分,非饱和延误是绿灯刚启亮时直行车辆以非饱和时距通过停止线所造成的损失时间,由于第4辆车之后的直行车辆的延误时间很小,在这里忽略不计,一般非饱和延误是由前2~4辆直行车造成的,待行区内储存的车辆数有可能少于4辆,故车辆起动延误存在2种可能,以下分别进行讨论[13,14]:
(1)待行区内储存的车辆数N≥4辆

(2)待行区内储存的车辆数N<4辆
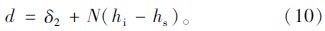
待行区设置前后影响直行相位的有效绿灯时间,设置待行区后,根据交通流波动理论,排队车辆开始运行时产生启动波,并且该波以机动车畅行车速Vf向后传播。因此,第1停止线后的第1辆车启动波经过时间LAB/Vf传至第2停车线后第1辆车。考虑启动波向后传播的时间[9],故第2停止线后面的直行车的有效绿灯时间为g′e,则有:
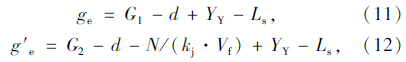
未设置待行区直行车道通行能力为N1。设置后直行车辆数由2部分组成:一是根据有效绿灯时间与饱和时距计算出的车辆数;二是在待行区内储存的车辆数,饱和时距与是否设置待行区没有关系,故值不变,设置待行区后进口道直行车道的通行能力为N′1。通行能力计算如下所示:
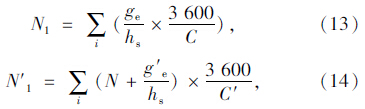
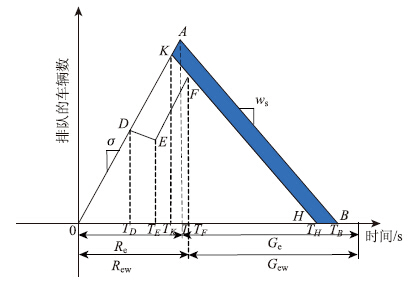
交叉口的平均控制延误等于均匀延误、随机延误和初始排队延误之和。直行待行区的设置影响到其中的均匀延误和随机延误的增量。如图 4所示,无待行区时直行车辆的排队长度在TA时刻达到最大值,在TB时刻消散完所有的排队车辆,三角形SOAB的面积就等于直行车辆的均匀延误。设置待行区后前N辆车从时刻TD到时刻TE进入待行区等待,在TF时刻直行信号灯显示绿灯,即第1停止线后面的直行车辆在时刻TF开始消散,在TH时刻消散完所有的排队车辆。有待行区后均匀延误时间分2部分计算,一是第1停止线后的直行车辆的延误时间,即多边形区域SODEFH的面积;二是提前进入待行区的N辆车的延误时间,即多边形区域SDKFE的面积,因此整个均匀延误时间就是三角形SOKH的面积,阴影部分的面积是设置待行区后减少的延误时间。均匀延误时间可以用以下公式计算:
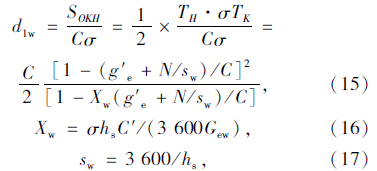
|
| 图 4 待行区设置前后延误模型图 Fig. 4Delay model before and after setting waiting area for through vehicles |
直行待行区的设置使得交叉口内的冲突距离发生了变化,在同样的周期时长下该相位的绿灯间隔时间增加,绿灯时间减少,随机延误的计算公式如下所示:
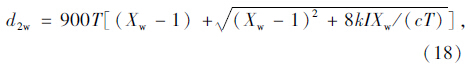
得到了平均均匀延误和平均随机延误之后,直行车辆的平均控制延误dw用式(19)求得:

以北京市典型交叉口—官园桥为例,该交叉口由双向6车道汇集而成。该交叉口东、西进口道分别渠化为3条左转专用车道、3条直行车道和1条专右车道;南进口道为2条专左车道、2条直行车道和2条专右车道;北进口道有2条左转车道、3条直行车道和1条专右车道。对南北方向的直行车道进行渠化,合理设置直行待行区,在南北直行车道不同饱和度和流量比情况下和对整个设置待行区前后整个交叉口进行多次仿真,仿真结果如图 5~图 8所示。
|
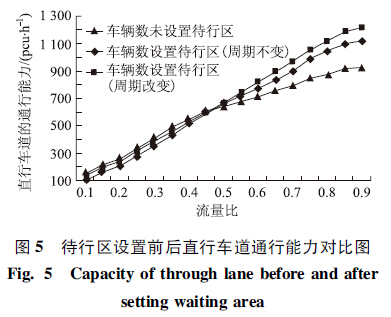
| 图 5 待行区设置前后直行车道通行能力对比图 Fig. 5Capacity of through lane before and after setting waiting area |
|
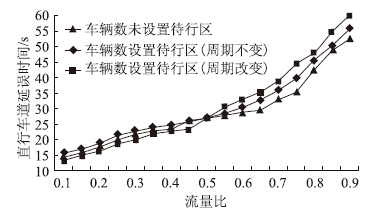
| 图 6 待行区设置前后直行车道延误时间对比图 Fig. 6Comparison of delay of through lane before and after setting waiting area |
|
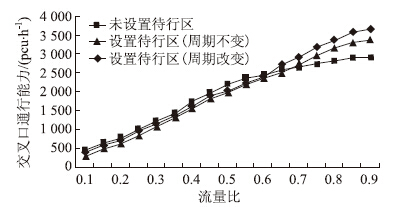
| 图 7 待行区设置前后交叉口通行能力对比图 Fig. 7Comparison of capacity of intersection before and after setting waiting area |
|
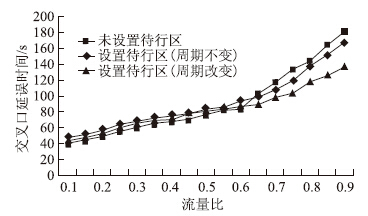
| 图 8 待行区设置前后交叉口延误时间对比图 Fig. 8Comparison of capacity of intersection before and after setting waiting area |
如图 5所示,当流量比较小时,待行区反而不利于通行能力的提高,尤其是周期不变的情况下,原因是流量比小时,车流量不是很大,排队的车较少,待行区停止线的前移缩短冲突点的距离,绿灯间隔时间有所增大,故在流量比小的情况下需要慎重考虑;流量比小时设置待行区能有效地提高直行车道的通行能力,尤其是在周期变化的情况下尤其显著,原因是道路车流量较大时,虽然待行区的设置使绿灯间隔时间增大,但排队车辆提前进入待行区等待,充分利用交叉口的空间区域,提高直行车道的利用率,最大限度地提高直行车道的通行能力。
如图 6所示,流量比较小时,设置待行区反而会导致延误时间的增加,主要是由于流量比小时,直行车道流量不多,无需设置直行待行区,而设置待行区致使停止线前移,绿灯间隔时间增大,无论周期是否改变,势必要减少绿灯时间,虽然车辆可以提前进入待行区,但是由于车辆少,无法真正起到空间和时间的相互转换,致使延误增加。当流量比大时,设置待行区能有效降低延误时间,随着车流量增多,排队的车辆增加,车辆提前进入待行区等待,达到时间和空间的相互转换,减少了延误时间。
如图 7、图 8所示,在流量比较小时,设置待行区不利于提高交叉口的通行能力,反而还增加延误时间,主要是此时各个进口道的排队车辆不多,在有限的绿灯时间内能通过交叉口,而待行区停止线的前移,增加绿灯间隔时间,导致延误增大;当流量比较大时,尤其是趋近1时,进口道车辆排队增加,在有限的绿灯时间内无法全部消散,容易导致二次排队,此时设置待行区,能达到时间和空间的相互转换,提高交叉口的通行能力,降低了延误时间。
3.2 模型验证 3.2.1 数据采集
调研官园桥路口早晚高峰和平峰的交通流量,流量如表 1所示。
| 时段 | 南进口道 | 北进口道 | 西进口道 | 东进口道 |
| 左转/直行 | 左转/直行 | 左转/直行 | 左转/直行 | |
| 早高峰 | 527/1 632 | 453/1 688 | 1 042/1 016 | 698/1 310 |
| 晚高峰 | 557/1 712 | 489/1 578 | 964/1 132 | 574/1 289 |
| 平峰 | 329/1 067 | 254/1 068 | 652/756 | 398/815 |
根据调研得到的交叉口现状交通流状况,在南北方向设置直行待行区,结合交叉口几何条件和交通数据,在仿真软件模拟设置待行区后的交通仿真,得出结果如表 2、表 3所示。
| 南北直行车道 | 通行能力 | ||||
| 早高峰 | 晚高峰 | 平峰 | |||
| 未设待行区 | 仿真数据 | 1 289 | 1 316 | 745 | |
| 模型数据 | 1 324 | 1 395 | 798 | ||
| 设置待行区 | 仿真数据 | 1 496 | 1 523 | 719 | |
| 模型数据 | 1 516 | 1 574 | 715 | ||
| 提高率/% | 16.1 | 15.7 | -3.4 | ||
| 南北直行车道 | 延误 | |||||
| 早高峰 | 晚高峰 | 平峰 | ||||
| 未设待行区 | 仿真数据 | 98.2 | 106.4 | 60.7 | ||
| 模型数据 | 86.9 | 91.8 | 63.1 | |||
| 设置待行区 | 仿真数据 | 87.5 | 92.6 | 62.3 | ||
| 模型数据 | 86.9 | 91.8 | 63.1 | |||
| 减少率/% | 11.5 | 13.7 | +2.6 | |||
(1)通行能力
由表 2知早晚高峰期,设置待行区后提高交叉口通行能力,平峰时是否设置待行区对通行能力的提高影响不大,甚至会降低直行车道的通行能力,进一步论证了上述的观点。设置待行区前后仿真数据与本文提出的模型计算出来的数据大致一致,验证本文模型的正确性。
(2)延误
由表 3易知,早晚高峰时设置待行区,降低直行车道的延误,平峰时期,是否设置待行区对交叉口影响不大,甚至会增加延误时间,进一步证实了以上的论述。设置待行区前后仿真数据与本文模型计算出来的数据大致一致,验证模型的正确性。
4 结论设置直行待行区在一定程度上提高交叉口内部空间资源的利用率,但是并不是所有的交叉口都适合设置待行区。一般在路口空间区域较大且无法满足交通需求时,通过设置待行区达到充分利用时空资源,减少延误,增加通行能力的目的。但是否需要设置待行区还应根据路口的实际交通状况进行可行性分析,经大量仿真分析验证在流量比达到一定的条件时,待行区才能充分发挥优势,进一步缓解交通压力。
| [1] | SUN D, BENEKOHAL R F. Analysis of Work Zone Gaps and Rear-end Collision Probibility[J]. Journal of Transportation and Statistics,2005, 8(2): 71-86. |
| [2] | 陆化普. 城市交通现代化管理[M]. 北京:人民交通出版社,1999. LU Hua-pu. Urban Transportation Modernization Management[M]. Beijing: China Communications Press, 1999. |
| [3] | 尚申德,王山川,王文红. 信号交叉口直行待行区的设置研究[J].中外公路,2010,30(1):29-31. SHANG Shen-de, WANG Shan-chuan, WANG Wen-hong. Research on Setting of Straight Waiting Area in Intersection[J]. Journal of China & Foreign Highway, 2010,30(1):29-31. |
| [4] | 左天福, 陶晟陶.关于设置平面交叉口直行待行区的思考与实践[J].交通与运输, 2011,(1): 21-25. ZUO Tian-fu, TAO Sheng-tao. Study and Practice on Waiting-area for Through Vehicles at Grade Intersection[J]. Traffic & Transportation,2011,(1):21-25. |
| [5] | 李小帅,贾顺平,孙海瑞. 机动车待行区设置方法的实证研究[J]. 交通运输系统工程与信息,2011,11(增1):194-200. LI Xiao-shuai, JIA Shun-ping, SUN Hai-rui. Study on the Methods of Establishing Waiting Areas for Auto-vehicles Turning Left and Going Straight at Signalized Intersections[J]. Journal of Transportation Systems Engineering and Information Technology, 2011,11(S1):194-200. |
| [6] | 杨明.直行待行区平面交叉口交通组织及通行能力研究[D]. 武汉:武汉工业学院,2009:35-37. YANG Ming. Study on Organization and Capacity of Waiting-area for Through Vehicles at Grade Intersection[D]. Wuhan: Wuhan Polytechnic University, 2009: 35-37. |
| [7] | GAO L, MAO B, LIU M, et al. Modeling and Simulation on Left-turn Waiting Area at Isolated Signalized Intersection[C]//2009 International Conference on Measuring Technology and Mechatronics Automation. Los Alamitos: IEEE, 2009,(2): 255-258. |
| [8] | 倪颖,李克平,徐洪峰.信号交叉口机动车左转待行区的设置研究[J]. 交通与运输,2006(2):32-36. NI Ying, LI Ke-ping, XU Hong-feng. Research on Waiting-area for Left-turning Vehicles in Signalized Intersections[J]. Traffic & Transportation, 2006(2):32-36. |
| [9] | 刘宇鹏.信号交叉口直行车道通行能力研究[D]. 吉林:吉林大学,2009:40-41. LIU Yu-peng. Research on Capacity of Straight Lane at Signalized Intersection[D]. Jilin: Jilin University, 2009:40-41. |
| [10] | 臧晓冬,周伟.基于车头间距变量的通行能力理论模型[J].公路交通科技,2010,27(2):103-107,113. ZANG Xiao-dong, ZHOU Wei. Theoretic Capacity Model Based on Variable Space Headway[J]. Journal of Highway and Transportation Research and Development, 2010,27(2):103-107,113. |
| [11] | 马万经,聂磊,杨晓光.单点定时信号最优控制模型及仿真分析[J].系统仿真学报, 2007, 19 (19):4543-4547. MA Wan-jing,NIE Lei,YANG Xiao-guang. Optimization Model and Simulation Analyses of Pre-timed Signals Control at Isolated Intersections[J]. Journal of System Simulation, 2007,19 (19): 4543-4547. |
| [12] | 王秋平,谭学龙,张生瑞.城市单点交叉口信号配时优化[J].交通运输工程学报, 2006, 6 (2): 60-64. WANG Qiu-ping, TAN Xue-long, ZHANG Sheng-rui. Signal Timing Optimization of Urban Single-point Intersections [J].Journal of Traffic and Transportation Engineering, 2006, 6 (2): 60-64. |
| [13] | 张萌萌,贾磊,邹难,等.单点交叉口鲁棒优化信号配时研究[J].公路交通科技,2011,28(1):107-111. ZHANG Meng-meng, JIA Lei, ZOU Nan, et al. Robust Optimal Traffic Signal Timing of Urban Single-point Intersection[J]. Journal of Highway and Transportation Research and Development, 2011, 28(1):107-111. |
| [14] | 吕斌,牛惠民. 随机条件下单点交叉口绿灯时间计算方法研究[J].公路交通科技,2010,27(2):108-113. LÜ Bin, NIU Hui-min. Calculation Method of Green Time for Pre-timed Signal Control at Isolated Intersection under Random Condition[J]. Journal of Highway and Transportation Research and Development, 2010,27(2):108-113. |
 2015, Vol. 31
2015, Vol. 31
