扩展功能
文章信息
- 杨晓芳, 周昱, 付强
- YANG Xiao-fang, ZHOU Yu, FU Qiang
- 考虑驾驶心理的封闭式道路车辆出匝换道模型
- A Lane-changing and Off-ramp Model of Vehicles on Enclosed Road Considering Driving Psychology
- 公路交通科技, 2015, Vol. 31 (7): 112-119
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (7): 112-119
- 10.3969/j.issn.1002-0268.2015.07.018
-
文章历史
- 收稿日期:2014-8-13
2. 同济大学 测绘与地理信息学院, 上海 200092
2. School of Surveying and Geo-informatics, Tongji University, Shanghai 200092, China
出口匝道前的车辆分流区作为高速公路、城市快速路等封闭式道路的重要基础组成部分,历来是道路通行能力的瓶颈地段,也是交通事故的频发区域[1]。分流区内车辆的出匝需经历换道、减速、驶离匝道等行为。这些行为导致主线车辆在各车道间重新分布,使得交通流变得紊乱且复杂,进而埋下了较大的交通安全隐患。对分流区内即将出匝车辆换道行为的研究,能梳理分流区的交通流规律,从而制订合理的交通管理措施来平衡车辆换道地点,安全有效地引导主线交通流导入匝道。因此,为了使封闭式道路分流区内的车辆能稳定、快速和安全地行驶,对出匝车辆驾驶人的驾驶心理及换道行为的研究很有必要。
目前,车道变换的研究主要侧重于换道类型判断、需求分析、间隙选择、实施换道等换道决策上[2,3,4,5,6,7],这些模型研究的对象通常是高速路的合流区和基础路段,较少有针对分流区特定车流的车道变更。对于分流区的研究而言,李秀文等[8]从分析分、合流影响区的交通运行特性入手,研究了分、合流影响区的通行能力。赵晓翠等[9]利用调研数据,通过速度提取总结了驾驶人驶入减速车道的3种驾驶过程。刘伟铭等[10]从调查数据中分析出换道特性,结合数理统计理论,应用微分法建立了超车道车辆的出匝换道模型。由此可见,已有分流影响区的研究主要集中在交通流特性上,对出匝车辆的具体运行规律的研究仍有不足,特别是没有考虑出匝过程中驾驶人的一系列心理变化对驾驶行为的影响。
为了改进已有模型的不足,本文引入换道紧迫感的概念,来量化车道数、减速车道长度、交通标志牌设置、交通流量、行驶车速等交通环境对驾驶心理的影响,试图揭示封闭式道路即将出匝车辆换道-驶离行为的特点和规律,进一步为交流区内交通设施的设计及宏观控制决策提供科学依据。
1 换道紧迫感对驾驶心理的影响分析驾驶心理是影响驾驶决策的直接因素,道路交通环境则作用于驾驶人的驾驶心理。驾驶人产生出匝意图后,首先会通过车窗对前方路段进行观测,在获取本车与匝道鼻端的距离、右侧车道数、视野内车辆数等交通环境信息后,对这些信息进行处理,做出相应的决策。对于不同驾驶人来说,其对交通信息的处理结果并不完全一致,但都是判断是否存在充足的操作时间与换道空间。若换道空间充足,驾驶人为了追求行车速度可能会在原车道上继续行驶,直到恰当的地点进行换道;若换道空间不足,驾驶人往往会担心无法顺利出匝,更倾向于提早换道。
为了描述这一现场,本文引入换道紧迫感的概念,将其定义为当前车辆所在位置拥有的剩余换道空间与换道所需最少空间的比值。其中,剩余换道空间不仅与当前车辆所在位置距离匝道鼻端的距离有关,也与右侧车道上的车辆数密切相关。右侧车道上车辆会占用一定的换道空间,车与车较近时所占用的空间互相叠加,车与车较远时所占用的空间互不影响。实际运营中的车辆分布是随机变化的,但服从均匀分布的车辆所占用的空间最大,以此来计算较为合理。据此,本文采用式(1)计算换道紧迫感来描述驾驶员的驾驶心理。
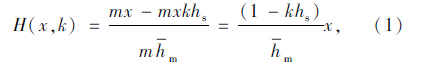
的最小安全距离,即车身长度加上最
短的安全跟车距离;h-m为驾驶人变换一次车道所需最少安全距离的均值;k为分流区交通流密度,可根据文献[11]将流量q、速度v与密度k进行转换,即k=f(q,v)。
假设驾驶人在产生出匝意图后,会立刻产生一个较大的初始值,随着剩余驾驶空间的减少,H(x,k)数值会逐渐降低,当H(x,k)减小到小于或等于1时,驾驶人没有充足的换道空间,则会导致驾驶人不得不停车等待,部分驾驶人甚至会采取激进的换道措施,强行插车汇入右侧车道,诱增交通事故的发生。
1.1 换道紧迫感对换道决策点的影响
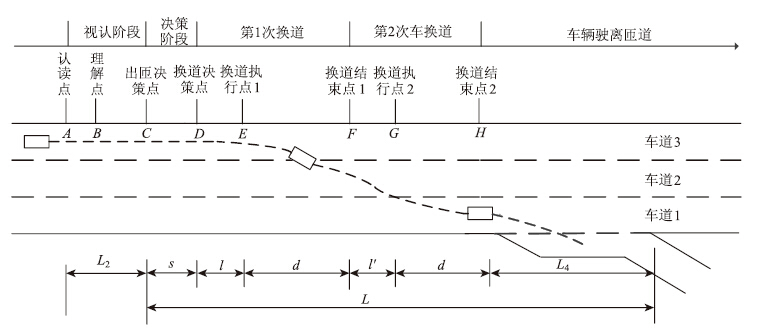
在分流影响区内,车辆的出匝步骤可以分为出匝信息获取、判断与决策、换道,如图 1所示。其中,车辆出匝信息获取阶段是驾驶人对交通标志的视认过程;判断与决策是驾驶人依据道路交通环境进行驾驶决策的阶段;换道是出匝车辆通过换道并最终驶入匝道的阶段。已有的出匝换道模型[12],通常将驾驶人对交通标志的认识过程分为认读、理解、消失、决策和操作5个步骤。其中驾驶人的出匝换道意图点为一固定值,可理解为驾驶人对交通标志视认后会立刻进行换道。但实际上在换道空间充足且交通环境宽松的情况下,驾驶人为了追求速度通常会在原车道上继续行驶一段距离,而非立刻进行车道变更。显然,不区分出匝决策点及换道决策点的出匝模型会对驾驶人的实际换道地点的估测会产生偏差,不利于分流区内交通设施的规划设计。据此,本文将决策点分解为出匝意图点和换道意图点,其中出匝意图点即驾驶人观测到交通标志并进行判定是否出匝的位置,换道意图点即驾驶人经过一系列的心理条件反射准备换道的意图点,执行点为出匝车辆驾驶人实际进行换道的位置。以三车道为例,车辆换道出匝过程可分为图 1中的8个点。图中,L为驾驶人产生出匝意图时距离匝道口的距离;S为驾驶人产生出匝意图到驾驶人产生换道意图间所行驶的距离;l(l′)为换道等待距离;d换道过程中产生的位移;L2为反应接受距离;L4为减速车道长度。
|
| 图 1 考虑驾驶心理的车辆换道出匝轨迹图 Fig. 1Trajectory of vehicle lane-changing and off-ramp considering driving psychology |
有出匝需求的驾驶人在点A开始对交通标志进行视认,到达点B成功获取交通标志信息,经过一段时间的判断与决策,在点C产生出匝意图,并依据道路交通状态获取一个初始的换道紧迫感Hc。若Hc数值较大,则车辆会在路段上继续行驶。随着剩余换道空间的减少,换道紧迫感系数也会逐渐降低,直到减至阈值Hd时,驾驶人就会产生换道意图,即图 1中的点D。若Hc数值小于阈值Hd时,驾驶人在点C就会产生换道意图,此时出匝意图点与换道意图点相互重叠。换道阈值Hd的取值可通过对不同流量条件下驾驶人的实测数据统计分析得到,即:
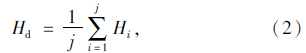
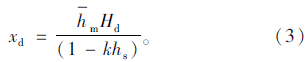
图 1中出匝-换道决策距离S为:
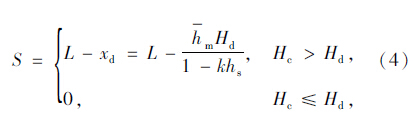
驾驶人行为会受到如路网流量、跟车距离、车辆特征、驾驶视野等因素的刺激影响,不同驾驶人对外界刺激的反应程度不同。为了便于研究,本文假设所有驾驶人的驾驶特征相同,即在相同条件下会做出同样的选择,结合间隙接受理论来描绘车辆换道出匝过程。驾驶人在图 1中点D处产生换道意图的同时,同样产生一个初始可接受的安全插入间隙td。若此时驾驶人右侧的车头时距大于td,则驾驶人会成功换道;否则,驾驶人不得不在原车道上继续行驶等待下一个符合条件车头间距的到来。而可插入车头间隙大小的选择并非固定不变,会随驾驶心理而发生改变。当车辆不断向前行驶时,驾驶人对于在匝道鼻端处仍然不能成功换道而导致停车的担忧越来越强烈,因而对临界间隙大小的选择会随着换道紧迫感的减少而逐渐降低。关羽和张宁考虑车辆汇入过程中临界间隙变化的情况,认为临界间隙与行驶时间呈线性递减关系[13]。根据文献[13]的相关结论,假设驾驶人对临界间隙的选择随着换道紧迫感的减少而线性减小,如图 2所示。

|
| 图 2 空间急迫感和临界间隙的关系 Fig. 2Relation between space urgency and critical gap |
根据前文分析可知,当空间紧迫系数H(x)>Hd时,驾驶人不会选择换道;随着换道紧迫感H(x) 的逐渐降低,驾驶人对临界间隙的选择也会逐渐降低,至到H(x)=1时,驾驶人对可穿插间隙的选择为最小临界可穿插间隙tm;当H(x)<1时,换道空间不足。则由图 2可得到临界间隙tc(x)与驾驶人换道紧迫感的关系式:
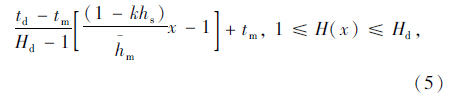
车辆出匝属于强制性换道的范畴,其过程包括换道等待距离ll′和换道过程中产生的位移d(见图 1)。若驾驶人在换道过程中沿斜直线行驶,设其与道路前进方向的偏转夹角为θ,车道宽度为W,则位移d=W/tan θ。换道等待距离与右侧车道上某点处出现可汇入间隙的概率密切相关,而概率的大小是符合一定分布的,比较成熟的连续交通流车头时距分布模型通常有拉格朗日分布、负指数分布、移位负指数分布、Cowan M3分布等。其中,负指数分布和移位负指数分布均可看作是Cowan M3分布的特殊形式;拉格朗日分布的公式推导非常复杂;Cowan M3分布具有形式简便、精度较高、参数容易获取的特点。据此,本文选用Cowan M3模型对车辆换道出匝行为进行推导,其车头时距F(t)的分布和定义为:
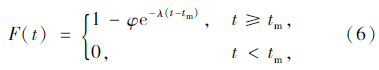
为了求得换道等待距离的长度,设点D处y=0,车辆在y=0开始行驶至y=l处成功换道的概率为p(l)。依据微分法可知车辆在y=l+Δl处(其中Δl→0)成功汇入的概率p(l+Δl)为:

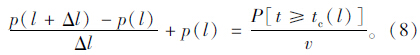
由图 1和式(4)可知:l=L-s-x。将式(5)代入式(6)则有:
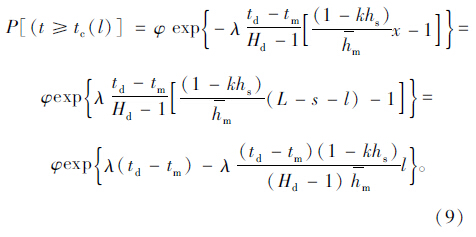
为了便于计算,此处令A=λ(td-tm),B= 式(9)可化简为:
式(9)可化简为:
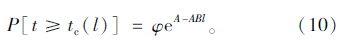
将式(10)代入式(8)可得到:
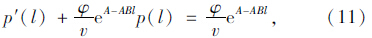
对式(11)求解,可知:
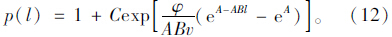
依据方程(12)的连续性及l的实际物理意义能获知,在产生换道意图的初始点,车辆均未能成功换道,即l=0时p(l)=0。将其代入式(11)得到C=-1。于是,出匝车辆在车道上行驶到y=l处还没未完成合流的概率pd(l)为:
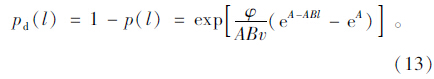
将l=L-s-x代入式(12)中,可得到车辆第1次换道时离上游鼻端的距离为x的概率是:
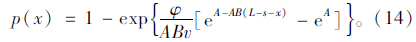
若此时车辆行驶在第2车道上,那么车辆换道时离匝道鼻端的距离为x的概率是:
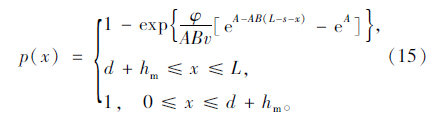
若车辆行驶在第3车道上,经历第1次成功换道后,驾驶员会对车辆所在位置右侧车头间距进行判断。如果此时车头间距大于tc (L-l-d),则车辆会保持斜直线继续行驶,最终抵达第1车道上。这种直接汇入式的换道概率为P[t≥tc(L-l-d)]=φe-λ [tc(L-l-d)-tm], 换道模型只需将式(14)中d修正为d′=2d即可。如果此时不满足换道条件,则车辆会在第2车道上正常前进,等待下一个可穿插间隙的到来。在忽略各车道间的相互影响的情况下,车辆在第2次换道中,第2车道上行驶距离为l′的概率是:
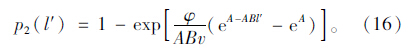

对封闭式道路车辆出匝特性的研究发现,车辆换道规律不仅与驾驶人特性有关,同样与分离区内交通设施的设置密切相关。这些设施主要包括车道数、车道宽度、最终预告指路标志牌、减速车道等。通常来说,车道宽度、车道数及减速车道长度在道路规划设计之初会参照文献[15],依据实际需求给出具体的设置方案。但有关指路标志牌位置的设置一般采用经验值,各类规范及标准中均未能给出契合实际、因地制宜的设置方案。
本文提出的车辆出匝换道行为的研究起点是驾驶人有充足的换道时间与空间。换道意图点距离匝道鼻端长度L是由驾驶人视认距离L1、反应接受距离L2、交通标志牌离匝道鼻端距离L3及减速车道长度L4来确定的,满足L=L1-L2+L3+L4。其中,驾驶人视认距离与交通标志牌类型、可见度、驾驶人类型等因素密切相关[16];驾驶人类型和车辆行驶速度会影响反应接受距离L2的长度[17];减速车道长度L4需依据道路的车流量和转出概率来合理设置[18]。为了保障所有车辆均能安全顺利出匝,交通标志牌位置距离L3的设置必须考虑最极端条件下的换道情形。因此,研究对象是采用最大设计时速在最左侧车道上行驶的冒险型驾驶人,研究目标是保障所有车辆能在靠近上游鼻端时顺利换至最右侧车道。采用小概率事件原理进行分析,可获知当车辆产生换道意图后继续行驶了一段距离x,还未完成合流的概率pd(x)足够小时,所对应的换道行驶距离才使几乎所有驾驶人在不停车情况下成功换道。设此小概率为α,则可求得小概率下pd(x)<α下车辆的换道行驶距离l。以双车道为例,此时L3需满足式(18)才能保障所有车辆顺利出匝。
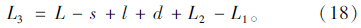
由此可见,对分流区出匝车辆的研究不仅能获取分流区驾驶人的驾驶特性,同样也有利于对封闭式道路车辆的交通控制和管理,更能因地制宜地为分流区内指路标志等交通设施的设置提供理论依据。
4 实例分析 4.1 模型对比分析文献[10]中提出了一种高速路超车道车辆出匝模型,并利用其相关结论采取指数曲线y=1-aebx对表 1中的实测车辆特征数据进行拟合,回归计算后得到模型:
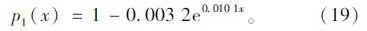
| 调查数据区间/ (×100 m) |
离上游鼻端距离 分布概率 |
调查数据区间/ (×100 m) |
离上游鼻端距离 分布概率 |
| 0~1 | 0.998 66 | 6~7 | 0.165 00 |
| 1~2 | 0.982 63 | 7~8 | 0.082 83 |
| 2~3 | 0.933 20 | 8~9 | 0.021 38 |
| 3~4 | 0.818 97 | 9~10 | 0.002 67 |
| 4~5 | 0.595 86 | ||
| 5~6 | 0.338 68 |
本文引用文献[10]中的数据,并采取相同的数据处理方式,即选取0~700 m内的调查数据,以区间中点对应离上游鼻端距离分布概率做散点图。并利用式(15)的相关结论得到的曲线形式y=1-exp(aebx)进行拟合,拟合后得到模型:
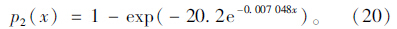
将x=150 m分别代入式(19)和式(20)中可获取:p1(150)=0.999 3,p2(150)=0.999 1。两者均与实测数据0.982非常接近,在接近上游鼻端时精度均较高,也证实很少有车辆在接近匝道鼻端时换道,符合实际情况。但当x=550 m时,p1 (550)=0.172 7,p2(550)=0.342 1, 两者与实测数据0.338 68对比分别相差49%和1%,显然本文提出的模型在分流区鼻端附近的精确度远高于文献[10],这是由于已有模型未能区分驾驶人的出匝意图点和换道意图点。同样,本文提出的模型对实测数据的拟合优度R2数值为0.996,高于文献[10]中模型的拟合优度0.894 3,拟合后的曲线更接近实际分布。综上所述,可以认定相对文献[10]中提出的出匝模型而言,考虑驾驶心理的车辆出匝模型整体精确度更高,更符合实际驾驶行为。

|
| 图 3 离上游鼻端距离分布概率拟合图 Fig. 3Fitting curves of distribution probability of distance from upstream nose |
为了证明模型的有效性和合理性,应用matlab编程对第2部分中模型参数的影响进行分析。若假定q=1 100 veh/h,v=110 km/h,Tc=5 s,τ=2 s,Hd=4,W=3.75 m,选用距离匝道出口300,350,400,450,500 m的中央横跨式标志牌对前文提出的车辆换道出匝模型进行分析,以三车道为例,其分析结果见图 4。图中概率曲线与x轴的交点可以理解为驾驶人在不同情况下的换道意图点。标志牌设置距离从远到近所设置的标志牌对应的驾驶人换道意图点分别为630,582,541,507,487 m,则在x轴上的间隔分别为48,41,34,20 m,数值均小于每类指路标志牌间距离50 m的间隔。这一现象是驾驶人依据道路交通状态自动调节的结果,符合实际驾驶情况。同样,当交通标志牌设置的距离低于 300 m 时,部分车辆行驶至分流区鼻端时仍无法换道,显然这种设置是不合理的。

|
| 图 4 指路标志牌位置设置对换道概率的影响 Fig. 4Influence of guiding signs’ setting distance on probability of lane changing |
主路流量也是影响分流区内车辆出匝车辆换道的重要因素之一。中央横跨式交通标志牌距离固定取值500 m,主路流量分别取1 000,1 100,1 200,1 400 veh/h,其他参数与4.2节相同。图 5给出了不同流量状态下两车道和三车道离上游鼻端距离的累积概率,可见:(1)相对三车道车辆而言,双车道车辆换道区间更大,换道地点更为分散。(2)低流量时两车道车辆在x=300 m处几乎全部成功换道,但三车道的出匝车辆仍有部分未能成功换道,进一步证实对于不同车道数的交通设施设置需要区分对待。(3)流量越低,驾驶人产生换道的意图越迟,但实际换道地点却远离匝道鼻端,整体换道地点更集中,这一特征是驾驶心理与右侧可穿插间隙出现概率相互作用导致的。以上现象也证实交通流量的增大,会使驾驶人的出匝换道行为更加激进。当流量增大到一定程度时,车辆速度变化区间极大,不符合前文假设,此时本模式不再适用。

|
| 图 5 不同交通流量下两车道和三车道车辆离上游鼻端距离的分布概率 Fig. 5Distribution probability of distance from upstream nose of 2-1ane and 3-1ane vehicles in different traffic volumes |
为了探究封闭式道路分流区内出匝车辆的运行规律,在已有模型的基础上,引入驾驶紧迫感系数的概念来量化驾驶人在换道出匝过程中的一系列心理变化,并利用微分法建立了考虑驾驶心理的车辆换道出匝模型。模型的对比分析证实了本文提出的出匝模型与实际数据拟合结果更合理,特别是分流区上游区域内的拟合明显优于原有模型。数值模拟分析了不同参数变化对于汇入概率的影响。模型最终揭示了车道数、减速车道长度、交通标志牌的设置、交通流量、车辆行驶速度等对驾驶人出匝换道行为的影响,能为封闭式道路交流区内交通设施的规划设计提供理论指导。然而,本文提出的模型在车流量达到饱和时不再适用,并且忽略了各车道之间变更车道造成的相互影响,这些仍需进一步的研究。
| [1] | 吴勇,刘新荣. 快速路路段类别事故率与交通流状态关系[J]. 中国公路学报,2013,26(3):150-157. WU Yong, LIU Xin-rong. Relationships between Crash Rates and Traffic Flow Conditions at Different Urban Express Artery Segment Types[J]. China Journal of Highway and Transport,2013,26(3):150-157. |
| [2] | NEWELL G F. A Simplified Car-following Theory: A Lower Order Model[J]. |
| [3] | ZHENG Zu-duo, AHN S, CHEN Dan-jue, et al. The Effects of Lane-changing on the Immediate Follower: Anticipation, Relaxation, and Change in Driver Characteristics [J]. |
| [4] | WANG C, COIFMAN B. The Effect of Lane-change Maneuvers on a Simplified Car-Following Theory[J]. |
| [5] | 李硕,张样. 高速公路主线流量对入口加速车道设计影响分析[J]. 中国公路学报,2000,13(2):108-111. LI Shuo, ZHANG Yang. An Application Study of Merging Theory on Designing Acceleration Lane for Expressway [J]. China Journal of Highway and Transport, 2000, 13(2): 93-97. |
| [6] | 智永锋,张骏,史忠科. 高速公路加速车道长度设计与车辆汇入模型研究[J]. 中国公路学报,2009,22(2):93-97. ZHI Yong-feng, ZHANG Jun, SHI Zhong-ke. Research on Design of Expressway Acceleration Lane Length and Merging Model of Vehicle[J]. China Journal of Highway and Transport, 2009, 22(2): 93-97. |
| [7] | 王江锋,邵春福,闫学东,等. 基于虚拟现实的车辆换道最小安全距离研究[J]. 公路交通科技,2010,27(8):109-113. WANG Jiang-feng, SHAO Chun-fu, YAN Xue-dong, et al. Research on Minimum Safety Distance of Lane Changing Based on Virtual Reality[J]. Journal of Highway and Transportation Research and Development, 2010,27(8):109-113. |
| [8] | 李秀文,荣建,刘小明,等. 快速路分、合流影响区交通特性及通行能力研究[J]. 公路交通科技,2006,23(1):101-104. LI Xiu-wen, RONG Jian, LIU Xiao-ming, ZHANG Zhi-yong, et al. Analysis of Traffic Flow Characteristics and Capacities of Diverging and Merging Influence Areas[J]. Journal of Highway and Transportation Research and Development, 2006,23(1):101-104. |
| [9] | 赵晓翠,杨峰,赵妮娜.高速公路互通立交分流区的驾驶行为[J].公路交通科技,2012,29(9):143-145. ZHAO Xiao-cui, YANG Feng, ZHAO Ni-na. Driving Behavior in Diverging Area of Expressway Interchange[J]. Journal of Highway and Transportation Research and Development, 2012, 29(9):143-145. |
| [10] | 刘伟铭,邓如丰,张阳,等. 高速公路出匝分流区超车道车辆车道变换模型[J].公路交通科技,2012,29(8):106-111. LIU Wei-ming,DENG Ru-feng,ZHANG Yang, et al. Vehicle Lane-changing Model for Overtaking Lane in Freeway off-ramp Diverging Area[J]. China Journal of Highway and Transport, 2012, 29(8): 106-111. |
| [11] | 邱荣华. 互通立交分流区交通流特性研究[D]. 南京:东南大学,2005. QIU Rong-hua. Research on Traffic Characteristic of Interchange Diverging Area[D]. Nanjing: Southeast University, 2005. |
| [12] | 李爱增,李文权,王炜. 城市快速路出口标志位置设置研究[J]. 交通运输系统工程与信息,2006,6(5):36-41. LI Ai-zeng, LI Wen-quan, WANG Wei. Research on Position of Traffic Sign on Urban Expressway Off-Ramp[J]. Journal of Transportation Systems Engineering and Information Technology, 2006,6(5): 36-41. |
| [13] | 关羽,张宁. 可变临界间隙条件下的加速车道车辆汇入模型[J].公路交通科技,2010,27(6):117-129. GUAN Yu, ZHANG Ning. Vehicle Merging Model for Acceleration Lane under Condition of Changeable Critical Headway[J]. Journal of Highway and Transportation Research and Development, 2010, 27(6):117-129. |
| [14] | AKCELIK R. Speed-flow and Bunching Models for Uninterrupted Flows[C]//Proceedings of Transportation Research Board 5th International Symposium on Highway Capacity and Quality of Service. Yokohama, Tokyo: Japan Society of Traffic Engineers, 2006. |
| [15] | GB5768—2009,道路交通标志和标线 第2部分:道路交通标志 [S]. GB5768—2009,Road Traffic Signs and Markings—Part 2:Road Traffic Signs[S]. |
| [16] | 潘晓东, 李君羡. 基于眼部行为的驾驶疲劳监测方法[J]. 同济大学学报: 自然科学版,2011,39(2):231-235. PAN Xiao-dong, LI Jun-xian. Eye State-based Fatigue Drive Monitoring Approach[J]. Journal of Tongji University: Natural Science Edition, 2011, 39(2):231-235. |
| [17] | GE Ru-hai,ZHANG Wei-wei,WANG Zhong.Research on the Driver Reaction Time of Safety Distance Model on Highway Based on Fuzzy Mathematics[C]//2010 International Conference on Optoelectronics and Image Processing.Haikou:IEEE,2010:293-296. |
| [18] | 王春娥. 高速公路立交变速车道长度研究[J].公路交通科技,2013,30(1):120-124. WANG Chun-e. Length of Speed-change Lane at Highway Interchange[J]. Journal of Highway and Transportation Research and Development, 2013,30(1): 120-124. |
 2015, Vol. 31
2015, Vol. 31
