扩展功能
文章信息
- 杨晓芳, 张盛, 付强
- YANG Xiao-fang, ZHANG Sheng, FU Qiang
- 基于博弈论的完全信息下的驾驶行为研究
- Research of Driving Behavior under Condition of Complete Information Based on Game Theory
- 公路交通科技, 2015, Vol. 31 (7): 105-111
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (7): 105-111
- 10.3969/j.issn.1002-0268.2015.07.017
-
文章历史
- 收稿日期:2014-6-9
2. 同济大学 测绘与地理信息学院, 上海 200092
2. School of Surveying and Geo-informatics, Tongji University, Shanghai 200092, China
车辆行驶过程中,驾驶员为达到理想的行车环境,需要根据道路信息的变化采取相应的驾驶策略。驾驶行为是一个复杂的过程,需要对诸多因素进行综合考虑,比较容易出现误判,造成交通事故。研究表明,95%左右的事故与驾驶员的故意违规和过错行为有关[1,2]。因此,研究驾驶行为很有必要。
国内外对于驾驶行为研究的开展大多从道路条件、危险驾驶、环境条件等角度为主进行研究,例如:D. Shinar等[3]研究了不同条件下的攻击驾驶行为。Y. Wang等[4]研究了路网上驾驶员的理性推理行为。Matjaz[5]通过引入博弈理论,研究了车辆间驾驶行为表现出来的宏观交通流特性。孙庆文等[6]基于不完全信息假设对演化博弈均衡进行了渐进稳定性分析。孙晓燕等[7]考虑车辆间的博弈特点,对交通流的影响进行了研究。在完全信息下,基于个体的、微观的交通特性研究还很少有所涉及。本文中的完全信息指交通参与者对其他参与者的特征、战略空间及收益效益函数都有准确的信息认知。基于此,展开基于博弈论的完全信息下的驾驶行为研究,对影响驾驶行为的几个主要因素(速度收益、临道车辆、时间演化、安全间距等)分别进行研究分析,以寻求各因素最优,进而为采取更有效的安全措施提供理论依据。
1 基于博弈论的完全信息下的驾驶行为基于博弈论的完全信息下的驾驶行为研究充分考虑了道路及行驶环境信息。通过研究驾驶员所侧重的不同需求或期望因素,得出能反映实际车辆行驶情况下的驾驶员行为策略。在驾驶行为的博弈中,完全信息与不完全信息相比较,前者是指驾驶员之间对实时信息了解的程度一致,后者是指了解程度不一致;前者是在信息条件相同的情况下,通过博弈行为在驾驶过程中获得各自收益,后者是在信息条件存在差异的情况下,博弈获得各自收益。完全信息更符合局部内交通信息一致的驾驶环境,驾驶行为的变化分析具有合理性。
基于博弈论的完全信息是指在行驶过程中所有驾驶员对道路信息达到共同认知的情况下,n位驾驶员各自选择行动形成不同的行动(战略)组合s1,s2,…,sn,由此决定各参与者的收益ui。根据实时信息条件,驾驶员会权衡利弊,做出基于自己利益的决策判断,在驾驶行为中具体表现为车辆的加减速、是否转向及其最终导致的跟驰或换道行为。由于驾驶员的行为是根据实时交通信息进行综合判断并做出调整的,涉及如可变信息版、诱导标志等实时道路信息,因此,本文选取信息化交通环境更为密集频繁的城市主干道上的驾驶员作为研究对象。
作为交通信息主要的作用对象——驾驶员而言,在完全信息下其行为可以看作是一个动态决策和反复调整的过程。基于驾驶员角度,其依靠自己的出行经验和接收的交通信息一起形成对实时信息的认知,并不断调整认知,从而判断是否需要以及如何改变驾驶行为。基于完全信息角度,改变后的驾驶行为作用于交通环境,使其状态也跟着改变,并以交通信息的形式反馈给出行者,从而引发新一轮的认知更新和出行行为调整过程。
2 完全信息下的驾驶行为分析在完全信息下,驾驶员根据道路交通的信息做出驾驶行为的决策,侧重于不同需求或期望的因素会导致决策后不同的驾驶行为。本文从影响驾驶行为的4个主要因素(速度收益、邻道车辆、时间演化、安全距离)分别进行研究论证。
2.1 基于速度收益因素在驾驶行为的博弈中,基于人对速度的期望,把前后车在跟驰换道过程中速度的变化量看作收益,对原先的博弈矩阵进行调整,收益的参数设置如下:前车的速度为v1,后车的速度为v2;前车的期望速度为v*1,后车的期望速度为v*2。这里的v*1和v*2反映了驾驶员在实际驾驶过程中对速度的期望值,不同的驾驶环境信息会导致不同的期望速度。当驾驶员达到期望速度v*时,就能满足在当前道路上基于速度的期望程度。
根据以上赋值,可得基于速度的收益矩阵为:
| F1 | C1 | |
| F2 | (v1-v2,0) | (v*2-v2,v*1-v1) |
| C2 | (v*2-v2,v1-v*1) | (v*1-v2,0) |
左上括号内第1项指后车在前车选择跟驰的情况下也选择跟驰,那么相对于前车,后车的速度收益为v1-v2;第2项指前车在后车选择跟驰的情况下也选择跟驰,那么相对于原来的速度不变,速度收益为0。
左下括号内第1项指后车在前车选择跟驰的情况下选择换道,那么相对于前车,后车的速度趋向于v*2,追求的速度收益为v*2-v2;第2项指前车在后车选择换道的情况下选择跟驰,那么相对于后车,其速度仍保持v1,没有选择追求期望速度v*1,那么后车的速度收益为v1-v*1。
右上括号内第1项指后车在前车选择换道的情况下选择跟驰,那么相对于前车,后车的速度趋向于v*2,追求收益为v*2-v2;第2项指前车在后车选择跟驰的情况下选择换道,那么相对于后车,前车的速度趋向于v*1,追求的速度收益为v*1-v1。
右下括号内第1项指后车在前车选择换道的情况下也选择换道,那么相对于前车,后车的速度在换道后依旧跟驰前车,将趋近于前车追求的期望速度v*1,那么后车的速度收益为v*1-v2;第2项指前车在后车选择换道的情况下也选择换道,那么相对于后车,前车就无速度变化优势,速度收益为0。
假设前车驾驶员选择换道的概率为x,则选择跟驰的概率即为1-x;后车参与者选择跟驰的概率为y,则选择换道的概率即为1-y。
选择跟驰和换道的后车参与者的期望收益分别为:
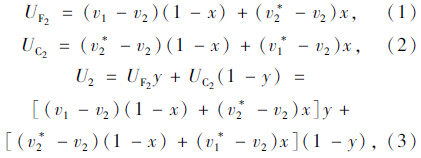
选择跟驰和换道的前车参与者的期望收益分别为:
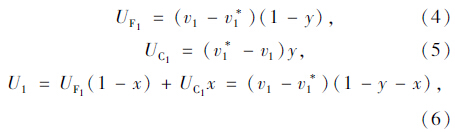
根据得到的前后车的期望收益,可知:
根据式(6),前车的速度比期望速度大时,即v1>v*1时,相对速度差Δv=v1-v*1,Δv越大,前车换道的概率x就越小,前车的期望收益就越大;如果后车跟驰的概率y越小,那么前车在不换道的情况下,在原车道继续行驶,也将增加前车的期望收益;当v1
对于后车而言,公式比较复杂。由于在驾驶行为中,驾驶员采用不同策略,通过一段时间的演化[8],会发现不同策略间的收益差异,并会相应改变当前策略,因此跟驰和换道的比例也不是固定不变的。根据这一特性,可得后车y的动态变化速度为[9]:
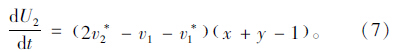
该式为后车驾驶员策略选择的时间演化模型,反映了后车驾驶员在前车不同的驾驶行为状态下,自身驾驶行为基于时间的演化过程。根据Friedman提出的局部稳定性分析[10],令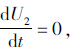 即收益趋近于稳定,即局部达到最优。
即收益趋近于稳定,即局部达到最优。
2.2 基于邻道车辆因素
在以速度为收益函数的博弈矩阵研究中,设前后车驾驶员的换道和跟驰战略的概率分别为p1=1-x,x,p2=y,1-y,那么这两位驾驶员选择的换道跟驰概率分布可构成二维联合概率分布如表 1所示。
| 驾驶行为 | 跟驰/% | 换道/% |
| 跟驰/% | (1-x)y | xy |
| 换道/% | (1-x)(1-y) | x(1-y) |
即当前车选择跟驰的概率为1-x,后车选择跟驰的概率为y时,两者同时选择跟驰的联合概率即为(1-x)y。以此类推,当前车选择跟驰时,后车同时选择换道的联合概率为xy;当前车选择换道时,后车同时选择跟驰的联合概率为(1-x)(1-y);两者同时选择换道的联合概率为x(1-y)。
这里,根据速度收益进行决策的换道行为,反映出驾驶员的一种驾驶行为意图。而在实际的车辆换道过程中,在原车道有换车意图的前提下,邻道有无可插车间隙直接决定了换道的成功与否。某时刻存在的可插车间隙,并不能保证下一时刻可插车间隙仍存在。此时,换道成功与否还取决于邻道的车辆驾驶情况,这里可分为邻道前车的影响和邻道后车的影响。
假设相邻道路前车速度为v01,相邻道路后车速度为v02,基于车辆的换道特性,分析可知:
(1)邻道只有前车或后车的情况
当v01>v*或v02
当v01
(2)邻道既有前车又有后车的情况
当v01>v*且v02
当v01
当v01>v*且v02>v*时,即邻道前车速度大于期望速度且邻道后车速度大于期望速度时,邻道前车保持当前速度,邻道后车跟驰邻道前车,缩小间距,与原车道打算换道的车辆构成博弈。
当v01
驾驶员在实际换道过程中,以邻道后车为例,其速度在大于期望速度的情况下,只要前方有空隙距离,仍会选择追上,与理论分析有所不同。这样,就让原车道前车和邻道后车之间又形成了一个博弈行为,原因在于原车道前车强行借道换道或邻道后车为了保持自身利益填补换道空隙。
在双方都理性驾驶的前提下,假设车辆本车道前车i=1,车辆邻道后车i=3,争取换道空隙的行为分为争取(Yi)和不争取(Ni),那么构成的收益矩阵为:
| Y3 | N3 | |
| Y1 | (u1Y1Y3,u3Y1Y3) | (u1Y1N3,u3Y1N3) |
| N1 | (u1N1Y3,u3N1Y3) | (u1N1N3,u3N1N3) |
| 邻道前车的影响 | 邻道后车的影响 | |||
| 基于期望速度 | v01>v* |
v01 | v02>v* |
v02 |
| 成功换道比例 | α1 | α2 | β1 | β2 |
表 3为本道前车在受到邻道前后车影响下,修正后的实际换道比例。在本道后车产生换道意图的情况下,上述分析仍然适用,邻道前后车始终制约着本道车换道行为的成功率。
| 实际换道比例/% | 邻道后车的影响 | ||
| v02>v* |
v02 | ||
| 邻道前车的影响 | v01>v* | α1β1x | α1β2x |
|
v01 | α2β1x | α2β2x | |
根据式(7)可知,后车驾驶员策略选择的时间演化模型与前后车速度、跟驰或换道的行为概率有关,可表示为:
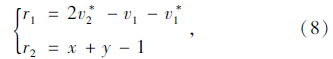
当r1r2=0时,时间演化模型达到稳态。即后车在前车的影响下达到了期望速度,驾驶员不需再调整驾驶行为的理想状态。
当2v*2>v1+v*1时,时间演化收益中的速度因素收益为正,此时,如果x+y>1,那么时间演化的整体收益为正;如果x+y<1,那么时间演化的整体收益为负。
当2v*2
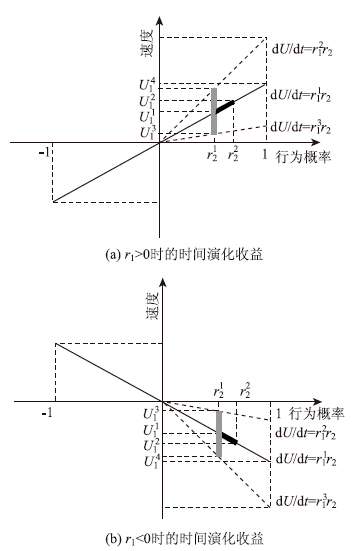
两者的时间演化收益如图 1所示。
|
| 图 1 随速度和行为概率变化的时间演化收益 Fig. 1Time evolution gains varying with speed and behavior probability |
图 1(a)为r1>0时,时间演化收益的变化情况。以r2>0为例,在行为概率因素相同的情况下,即r12处,当斜率r1不一样时(即速度因素不同),斜率r21>r31,时间演化收益存在差异,为ΔU=U4t-U3t,如灰线标注,斜率越大,时间演化收益越大;当斜率r11不变(即速度因素相同),当行为概率因素不同(r22>r12)时,时间演化收益存在差异,为ΔU=U2t-U1t,如黑线标注,行为概率因素越大,时间演化收益越大。当r2<0时,时间演化收益变化相反。
图 1(b)为r1<0时,时间演化收益的变化情况。以r2>0为例,在行为概率因素相同的情况下,即r12处,当斜率r1不同(即速度因素不同)时,斜率r21>r31,时间演化收益存在差异,为ΔU=U4t-U3t,如灰线标注,斜率越大,时间演化收益越小;当斜率r11不变(即速度因素相同),行为概率因素不同(即r22>r12)时,时间演化收益存在差异,为ΔU=U2t-U1t,如黑线标注,行为概率越大,时间演化收益越小。当r2<0时,时间演化收益变化相反。
理想状态下,当2v*2=v1+v*1时,基于速度因素,时间演化收益的斜率为0,后车收益为0,达到稳定状态。此时,基于时间因素,如果前车速度已趋近其期望速度,即v1=v*1,那么前后车之间速度关系变为v*2=v1=v*1,最终前后车在行驶过程中都达到了自己的期望速度。
这样,整体的速度演化效益将逐渐趋近于0,随时间演化的速度效益也将趋近最大值,即后车驾驶员都基本满足了基于个人利益的期望速度,只需要保持当前行驶状态正常行驶,就能保证速度收益。
2.4 基于安全间距因素 p> 在驾驶过程中,在前后两车进入博弈状态后,速度随时间演化的收益是影响驾驶员跟驰或换道行为的决策因素。这里,此期望收益是驾驶员从个人利益角度进行分析的。然而,在实际驾驶行为中,实时信息环境在一定程度上制约着驾驶员的决策行为。其中,前后车辆间的平均距离在驾驶过程中就制约着前后车间的实际驾驶行为[11,12]。在车辆行驶过程中,假设两车间的实际距离为s,存在一个安全间隔距离为s1,那么一般驾驶行为的变化如下:
(1)如果s<s1,后车需及时减速行驶,避免相撞。
(2)如果s>s1,后车会适当加速行驶,安全跟驰。
在博弈状态下,基于驾驶员对速度有期望需求,受安全间距因素的影响,驾驶行为的变化如下:
(1)当v2<v*,后车倾向换道,但s<s1时,后车要减速行驶,则后车的换道行为将受影响,只有当s>s1后,后车才能实现换道行为。
(2)当v2>v*,后车倾向跟驰,但s>s1时,后车仍有加速的可能,则后车的速度v2可能增加并接近前车的速度v1,改变驾驶行为。
综上所述,前者为在没有驾驶行为变化意图的情况下,驾驶员正常地根据安全间距影响因素调整自己的驾驶行为;后者为已产生驾驶行为变化意图的情况下,驾驶员根据实际安全间距影响因素改变自己的驾驶行为。
3 实例分析基于驾驶行为中存在的博弈关系假设,调查在实时信息环境下的实际路段,并定量分析驾驶行为在实际交通流中的变化。
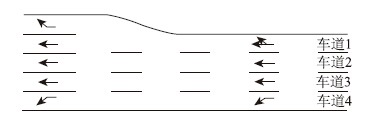
考虑模型的适用性,调查路段选取上海市海宁路(吴淞路—九龙路)方向路段。该路段为城市内部道路,平峰和高峰时段下的车辆变道频繁,驾驶行为变化种类多,影响驾驶行为的因素多。车辆行驶路段为四车道,在进入下一交叉口前,路段扩展为五车道,如图 2所示。
|
| 图 2 调查路段海宁路(吴淞路—九龙路)示意图 Fig. 2Schematic diagram of research section: Haining Rd.(Wusong Rd.—Jiulong Rd.) |
调查时间为1 h,对车辆驾驶行为的各项数据进行统计整理,调查时段的流量为600 veh/h。该路段上的驾驶行为按行驶路径的变化,可分为直行变右转、直行变左转和依旧直行等;按行驶意图的变化,可分为继续跟驰、当即换道、强制换道等。
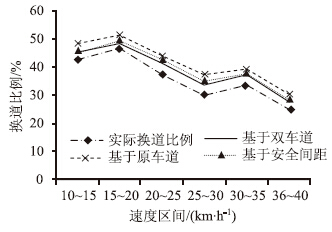
根据实例中采集到的车辆数据,对满足前后车博弈条件并构成博弈行为的车辆进行矩阵运算。考虑不同影响因素及不同影响程度的实时信息,获得不同速度区间和车辆换道比例的变化情况,如图 3所示。
|
| 图 3 基于博弈论的换道比例分布 Fig. 3Proportion distribution of lane-changing based on game theory |
在完全信息的假设条件下,实际统计到的换道比例随着速度的上升,总体呈下降趋势;基于原车道前后车博弈的换道比例趋势相同,但明显高于实际的换道比例;基于双车道前后车博弈的换道比例比本车道的换道比例更接近实际的换道比例;基于安全间距的换道比例则与基于双车道的换道比例相近。
基于本车道本换道比例的驾驶行为是本车道驾驶员基于前后车博弈行为得出的最利己的驾驶行为,但这种根据当前速度因素所得的是一种相对静态的驾驶行为意图,在接下来的实际动态换道过程中,会受到安全间距及临道车辆等因素的影响,导致实际换道不成功,所以基于本车道前后车的博弈行为得出的换道比例显著偏高。
基于双车道和安全间距的换道比例误差情况如图 4所示。误差1为基于本车道前后车博弈的换道比例与实际统计的换道比例的误差值,误差2和误差3分别为基于双车道的和安全距离的误差值。其中,基于双车道前后车博弈的换道比例误差率比基于本车道的平均误差率减少了8.13%,比基于安全距离的平均误差率减少了2.06%。
数据分析表明,基于博弈论的驾驶行为,在考虑本车道前后车之间的博弈性时,也同时考虑临道车辆的影响,即实时信息考虑得越多,与真实的驾驶行为就越接近。
速度所在的区间较小时,误差率较低,基于双车道前后车博弈的误差比例在速度区间10~15 km/h和15~20 km/h分别为5.5%和4%;在速度区间20~30 km/h呈上升趋势,在这个区间的驾驶员较为活跃,不可控因素多,最高误差率接近13%;在速度区间30~40 km/h稳定在10%左右。
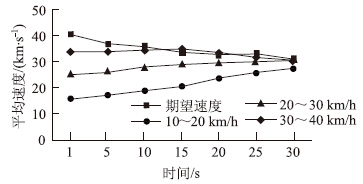
在以期望速度为主要因素的驾驶行为研究中,基于博弈矩阵的驾驶行为,在速度收益上的变化如图 5所示。该图表明,基于博弈的驾驶行为,不同速度区间的平均速度随时间推移的收益变化。其中,10~20 km/h的速度收益效果最明显,平均收益率为0.36 km/(h·s),收益趋势向期望速度靠拢;20~30 km/h的速度平均收益率为0.15 km/(h·s),最终随时间推移逐渐接近期望速度;30~40 km/h的速度平均收益分为两个阶段,第1阶段为速度收益向期望速度靠拢,平均收益率为0.14 km/(h·s),第2阶段为速度收益在期望速度附近摆动,平均收益率为-0.26 km/(h·s),随着期望速度的变化而变化,比前面的速度收益略有下降。
|
| 图 5 基于博弈行为的速度收益变化 Fig. 5Speed gain change based on game behavior |
本文采用基于博弈论的完全信息对驾驶行为进行了研究。考虑速度收益、临道车辆、时间演化、安全间距等因素后,建立了完全信息下的驾驶行为模型。通过与博弈论的驾驶行为换道比例的分析表明:(1)只基于本车道前后车的驾驶行为体现了驾驶员的驾驶行为意图,其换道比例大于实际行驶中的换道比例,如果同时考虑邻道前后车的影响,即基于双车道考虑,换道比例更接近实际情况;(2) 不同速度区间的速度收益随时间推移逐渐接近期望速度,所处的速度区间越小,收益幅度越大,所需达到稳定的时间越久。
但在实际应用中,该驾驶行为模型只适用于熟悉道路环境的驾驶员,存在一定的局限性。基于完全信息假设下的分析具有一定的简化性,与实际驾驶行为仍存在差异。如何将预测的驾驶行为更好地作用于当前的驾驶行为,仍需要进一步研究。
| [1] | LEE J D. Fifty Years of Driving Safety Research[J]. |
| [2] | ZHANG W, HUANG Y H, ROETTING M, et al. Driver's Views and Behaviors about Safety in China: What do They Not Know about Driving[J]. |
| [3] | SHINAR D, COMPTON R. Aggressive Driving: AN Observational Study of Driver, Vehicle, and Situational Variables[J]. |
| [4] | WANG Y, NAKAO A. On Cooperative and Efficient Overlay Network Evolution Based on a Group Selection Pattern[J]. |
| [5] | PERC M. Premature Seizure of Traffic Flow due to the Introduction of Evolutionary Games[J]. |
| [6] | 孙庆文, 陆柳, 严广乐, 等. 不完全信息条件下演化博弈均衡的稳定性分析[J]. 系统工程理论与实践, 2003, 23(7): 11-16. SUN Qing-wen, LU Liu, YAN Guang-le, et al. Asymptotic Stability of Evolutionary Equilibrium under Imperfect Knowledge[J]. Systems Engineering-Theory & Practice, 2003, 23(7): 11-16. |
| [7] | 孙晓燕, 汪秉宏. 考虑车辆间博弈行为的交通流[J]. 上海理工大学学报, 2012, 34(1): 14-17. SUN Xiao-yan, WANG Bing-hong. The Traffic Flow Considering Games between Vehicles[J]. Journal of University of Shanghai for Science and Technology, 2012, 34(1): 14-17. |
| [8] | 李振龙, 张利国. 超速驾驶行为的演化博弈[J]. 交通运输系统工程与信息, 2010, 10(4): 137-142. LI Zhen-long, ZHANG Li-guo. Evolutionary Game of Speeding Driving Behavior [J]. Journal of Transportation Systems Engineering and Information Technology, 2010, 10(4): 137-142. |
| [9] | 卢方元. 环境污染问题的演化博弈分析[J]. 系统工程理论与实践, 2007, 27(9): 148-152. LU Fang-yuan. Evolutionary Game Analysis on Environmental Pollution Problem[J]. Systems Engineering-Theory and Practice, 2007, 27(9): 148-152. |
| [10] | FRIEDMAN D. Evolutionary Games in Economics[J]. |
| [11] | 王江锋, 邵春福, 闫学东, 等. 基于虚拟现实的车辆换道最小安全距离研究[J]. 公路交通科技, 2010, 27(8): 109-113. WANG Jiang-feng, SHAO Chun-fu, YAN Xue-dong, et al. Research on Minimum Safety Distance of Lane Changing Based on Virtual Reality[J]. Journal of Highway and Transportation Research and Development, 2010, 27(8): 109-113. |
| [12] | 许伦辉, 罗强, 吴建伟, 等. 基于最小安全距离的车辆跟驰模型研究[J]. 公路交通科技, 2010, 27(10): 95-100. XU Lun-hui, LUO Qiang, WU Jian-wei, et al. Study of Car-following Model Based on Minimum Safety Distance[J]. Journal of Highway and Transportation Research and Development, 2010, 27(10): 95-100. |
 2015, Vol. 31
2015, Vol. 31
