扩展功能
文章信息
- 邵良杉, 徐波
- SHAO Liang-shan, XU Bo
- 基于因子分析与Fisher判别分析法的隧洞围岩分类研究
- Research on Classification of Tunnel Surrounding Rock Based on Factor Analysis and Fisher Discriminant Analysis
- 公路交通科技, 2015, Vol. 31 (7): 98-104
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (7): 98-104
- 10.3969/j.issn.1002-0268.2015.07.016
-
文章历史
- 收稿日期:2014-8-27
地下空间的开发与利用已经受到了人们的广泛重视,在地下岩体的施工过程中,隧洞围岩分类是一项重要的研究内容。围岩类别的确定是对岩体质量和稳定性的一种综合评价,同时也对地下工程稳定性、安全性起着非常重要的作用[1]。对围岩分类的预测方法研究受到了国内外学者的共同重视,国外的围岩分类方法有很多,如Q分类体系[2] 和RMR方法[3]。国内也有很多学者对此做出了研究,如传统的评价方法——普氏分类法[4],但是影响围岩稳定性的因素有很多,如地质构造、岩性、岩体结构和地下水等,传统的方法已经无法解决过程如此复杂的围岩分类问题。针对这种复杂性,我国许多学者采用多种地质因素组合来对围岩进行分类,该方法在实际工程应用中取得了一定的成果,并得到了广泛重视
目前,很多不同的方法已经被应用于围岩分类中,如模糊数学方法[5,6]、人工神经网络[7]、马氏距离判别法[8]、层次分析法[9]、Bayes判别分析法[10]、特尔菲-理想点法[11]、支持向量机[12]、非线性耦合分类技术[13]等多个指标的综合判别方法。这些方法都是各位学者针对不同的隧道围岩情况所提出的,在各自的研究领域内都作出了非常有意义的探索,但是也都有一定的局限性,如模糊数学方法在确定各个指标的权重时,主要依靠的是专家经验,有一定的主观性和随意性,而权重的确定是否合理直接关系到判别结果的准确性;基于先验知识的智能预测方法,如人工神经网络有其自组织性、极强的非线性逼近等优点,但该方法有收敛速度慢,容易陷入局部极小值的缺点,对参数的选择是否符合工程实际的问题还需要很好地解决;支持向量机方法在处理小样本事件时优势显著,但在应用过程中参数的确定比较困难。如果从作为围岩分类评判指标的因素来研究围岩的类别,避免各个因素之间的信息重合,可以更好地分析各个因素对围岩类别的综合影响。
基于以上研究,本文将借鉴因子分析可以浓缩数据的优点,结合Fisher判别分析(FDA)方法在无须知道原始数据分布情况下而对新样本进行判别的思想,建立隧洞围岩分类的因子分析-Fisher判别模型,对隧道围岩的类别进行预测,将其运用到实际的工程项目中,验证该模型的可行性和可靠性。
1 因子分析及Fisher判别分析计算理论1.1 因子分析
因子分析(Factor Analysis)是多元统计分析的一个重要分支,最初由英国心理学家C. Spearman提出。因子分析的主要目的是浓缩数据,通过对诸多变量的相关性研究,用少数变量来表示原来变量的绝大部分信息。目前,常用的因子分析类型有R型因子分析和Q型因子分析,前者是针对变量作因子分析,后者是针对样品作因子分析[14]。
根据研究需要,选用R型因子分析。设原有变量k个,分别为X1,X2,…,Xk,且每个变量经过标准化之后都是均值为0、标准差为1的标准化变量。因子分析的数学模型表示为:
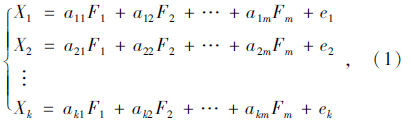


1.2 Fisher判别分析法的思想和求解
Fisher判别分析是由Fisher在1936年提出的,其基本思想是投影[15],即将高维数据点投影到低维空间上。投影的原则是将总体与总体之间尽可能地分开,然后根据类间距离最大、类内距离最小的原则确定判别分析函数,达到正确分类的目的,进而对新的样本进行分类判别[16]。
设有m个总体G1,G2,…,Gm,各总体的特征指标都是p个,相应均值向量和协方差矩阵分别为μ1,μ2,…,μm(p维),V1,V2,…,Vm(p×p阶)。
对于样本x=x1,x2,…,xpT,假定其判别函数为:
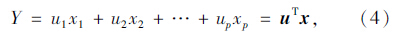
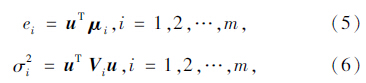
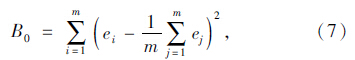
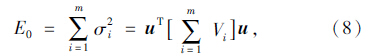
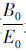 最大的u来作为判别函数Y=uTx中的系数向量。令
最大的u来作为判别函数Y=uTx中的系数向量。令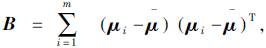
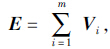 则B*=Bni为组间离差平方和,E*=Eni为组内离差平方和,其中ni(i=1,2,…,m)表示样本的数量。若λ是矩阵E-1B的最大特征根,那么对应于λ的特征向量u就是所要求的判别函数中的系数向量。通常,可以找出对应于E-1B的前几个较大特征根λ1,…,λt,且t≤minm-1,p,并根据贡献率
则B*=Bni为组间离差平方和,E*=Eni为组内离差平方和,其中ni(i=1,2,…,m)表示样本的数量。若λ是矩阵E-1B的最大特征根,那么对应于λ的特征向量u就是所要求的判别函数中的系数向量。通常,可以找出对应于E-1B的前几个较大特征根λ1,…,λt,且t≤minm-1,p,并根据贡献率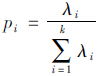 来选取特征根个数[15],进而找到其对应的特征向量uT1,…,uTt。采用不加权法对待判别样本x=x1,x2,…,xpT进行分类,记
来选取特征根个数[15],进而找到其对应的特征向量uT1,…,uTt。采用不加权法对待判别样本x=x1,x2,…,xpT进行分类,记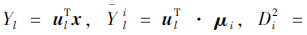
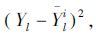 其中l=1,2,…,t;i=1,2,…,m,若D2i最小,那么x就属于Gi。
其中l=1,2,…,t;i=1,2,…,m,若D2i最小,那么x就属于Gi。1.3 Fisher判别函数效果的检验
为了检验建立的FDA模型的有效性和可靠性,可以采用回代估计法求误判率来进行判断[17]。将所有的训练样本作为n个新样本,依次代入建立的判别函数并进行判别。误判样本个数N与所有样本的比即为误判率η,η的计算公式为:

判别因子的恰当选取是建立Fisher判别模型的重要前提,一般情况下,为了使围岩分类更加准确,要尽量选取多个评判指标因子,但需要的工作量也会大大增加,耗费的计算时间会较长。因此,选择的评价因子要能够反映出岩体的岩体结构、地质构造、岩性等基本特征,同时结合各类指标,这些指标应具有广泛性、适用性和可操作性。根据《水工隧道设计规范》(SL279—2002)及国内外围岩分类经验[18,19]和研究成果[10],选取以下几个参数作为判别因子:(1)岩石质量指标RQD(X1),该指标反映岩块完整程度及其大小;(2)完整性指数Kv(X2),反映岩体的完整性程度;(3)饱和单轴抗压强度Rc(X3)(单位为MPa),反映岩块软硬特性及岩性特征;(4)纵波波速vp(X4)(单位为km/s),它在一定程度上反映岩体的完整程度以及刚度特征;(5)弹性抗力系数K0(X5),反映了围岩的综合物理力学性质,通常采用查表或者利用弹性公式来确定;(6)结构面摩擦系数f(x6), 它反映结构面粗糙程度、蚀变及充填情况[20]。根据文献[18]提供的广东省东江—深圳供水改造工程中的数据(表 1),运用SPSS17.0软件对所选的6个变量进行两两相关分析,以减少变量因素之间信息的冗余,提高相互独立性,求得Pearson Correlation及Sig.(2-tailed)检验结果:6个变量相互之间的t统计量的值显著性概率p均小于0.05,相关系数显著异于0,所以,彼此之间存在较强的相关关系。
| 序号 | 判别因子 | 实际类别 | 预测类别 | 第1个函数值 | 第2个函数值 | |||||||
| X1 | X2 | X3 | X4 | X5 | X6 | F1 | F2 | |||||
| 1 | 58 | 0.59 | 85 | 4 207 | 18 | 5 | -0.261 01 | 1.734 27 | 2 | 2 | 7.242 | -1.259 |
| 2 | 86 | 0.68 | 110.2 | 4 500 | 18 | 5 | 0.642 26 | 1.497 93 | 2 | 2 | 8.517 | -0.214 |
| 3 | 95 | 0.65 | 110.2 | 4 514 | 18 | 5 | 0.881 37 | 1.306 5 | 2 | 2 | 8.266 | 0.137 |
| 4 | 94 | 0.72 | 110.2 | 4 660 | 18 | 5 | 1.060 09 | 1.258 06 | 2 | 2 | 8.51 | 0.344 |
| 5 | 50 | 0.57 | 111.5 | 4 122 | 15 | 5 | -0.746 6 | 2.165 06 | 2 | 2 | 7.944 | -1.996 |
| 6 | 60 | 0.72 | 111.95 | 4 060 | 15 | 2 | -0.349 2 | 1.537 22 | 2 | 2 | 6.112 | -1.235 |
| 7 | 94 | 0.68 | 81.5 | 4 580 | 18 | 5 | 1.324 04 | 0.697 16 | 2 | 2 | 6.636 | 0.933 |
| 8 | 75 | 0.55 | 55 | 3 700 | 5 | 3 | 1.164 47 | -0.861 78 | 3 | 4* | -0.901 | 1.668 |
| 9 | 45 | 0.55 | 55 | 3700 | 10 | 4 | -0.103 31 | 0.508 02 | 3 | 3 | 2.051 | -0.396 |
| 10 | 62 | 0.46 | 55 | 3 695 | 10 | 4 | 0.264 26 | 0.175 11 | 3 | 3 | 1.489 | 0.165 |
| 11 | 64 | 0.53 | 59.5 | 4 000 | 10 | 4 | 0.551 31 | 0.127 41 | 3 | 3 | 2.019 | 0.482 |
| 12 | 70 | 0.53 | 59.5 | 4 014 | 10 | 4 | 0.754 95 | -0.015 35 | 3 | 3 | 1.898 | 0.769 |
| 13 | 66 | 0.42 | 68.5 | 3 580 | 8 | 4 | 0.221 59 | 0.183 88 | 3 | 3 | 1.418 | 0.117 |
| 14 | 55 | 0.46 | 61.84 | 3 280 | 8 | 4 | -0.098 67 | 0.317 15 | 3 | 3 | 1.192 | -0.282 |
| 15 | 81 | 0.5 | 55 | 3 956 | 10 | 4 | 1.088 44 | -0.337 49 | 3 | 3 | 1.296 | 1.29 |
| 16 | 52 | 0.52 | 68.7 | 3 965 | 10 | 4 | -0.003 01 | 0.613 98 | 3 | 3 | 2.797 | -0.356 |
| 17 | 44.5 | 0.5 | 20 | 3 000 | 1 | 1.5 | 0.389 87 | -1.345 49 | 4 | 4 | -5.13 | 1.166 |
| 18 | 61 | 0.52 | 20 | 3 959 | 3.5 | 3 | 1.327 04 | -1.452 62 | 4 | 4 | -3.176 | 2.171 |
| 19 | 70.5 | 0.49 | 40.9 | 3 000 | 3.5 | 3 | 0.876 89 | -1.075 76 | 4 | 4 | -2.628 | 1.501 |
| 22 | 42 | 0.24 | 62.7 | 2 690 | 2.5 | 1.75 | -1.034 73 | 0.035 99 | 4 | 4 | -1.538 | 0.315 |
| 23 | 25 | 0.27 | 18.5 | 2 500 | 3 | 2 | -1.041 17 | -0.403 81 | 4 | 4 | -2.525 | 2.878 |
| 24 | 31 | 0.26 | 25 | 2 950 | 2 | 1.5 | -0.719 76 | -0.630 33 | 4 | 4 | -2.533 | -1.063 |
| 25 | 22 | 0.25 | 8 | 1 900 | 1.5 | 1.25 | -1.253 | -0.696 87 | 5 | 5 | -4.559 | -0.816 |
| 20 | 33 | 0.5 | 38.3 | 3 896 | 3.5 | 3 | 0.091 14 | -0.388 78 | 4 | 4 | -4.756 | -0.363 |
| 21 | 85 | 0.53 | 38.3 | 4 014 | 3.5 | 3 | 1.917 76 | -1.647 2 | 4 | 4 | -6.45 | -0.861 |
| 26 | 34 | 0.14 | 16.3 | 2 060 | 1.5 | 1.25 | -1.130 73 | -0.748 2 | 5 | 5 | -6.366 | -0.709 |
| 27 | 24 | 0.18 | 16.3 | 2 330 | 1 | 1 | -1.239 89 | -0.663 78 | 5 | 5 | -6.265 | -0.867 |
| 28 | 33 | 0.13 | 14.5 | 1 960 | 1.25 | 1 | -1.204 84 | -0.794 19 | 5 | 5 | -6.769 | -0.757 |
| 29 | 20 | 0.17 | 10 | 1 960 | 1 | 0.75 | -1.488 59 | -0.666 06 | 5 | 5 | -6.923 | -1.116 |
| 30 | 8.5 | 0.15 | 6.3 | 1 952 | 1.25 | 0.75 | -1.880 98 | -0.430 03 | 5 | 5 | -6.868 | -1.647 |
| 注:“*”为误判样本 | ||||||||||||
由于选取的6个判别因子之间存在较强的相关关系,若直接将其作为Fisher判别模型的判别指标,会因变量之间的重复信息使模型缺乏可靠性,因此有必要对变量进行浓缩。首先检验这6个变量是否适合作因子分析,运用SPSS17.0对其进行KMO检验和Barlett检验并得到结果:样本的KMO值为0.852,很适合作因子分析;同时,Barlett球体检验的概率为0,小于显著性水平0.05,拒绝它的零假设,适合作因子分析。
2.3 Fisher判别模型的建立以《工程岩体分级标准GB50218—94》[21]为依据,结合工程实践经验,将岩体质量分为Ⅰ级、Ⅱ级、Ⅲ级、Ⅳ级、Ⅴ级5个等级,并将其类别值分别设定为1,2,3,4,5。根据文献[18]的隧洞工程中共涉及的6条隧洞(分别为观音山隧洞、笔架山隧洞、石山隧洞、窑坑隧洞、凤岗隧洞和走马岗隧洞)所处工程场地的地质条件,将其分类情况列于表 1。选取30个样本(表 1),建立基于因子分析的Fisher判别模型。对6个相关程度较高的变量作因子分析,提取适当个数的公共因子,将提取的公共因子作为Fisher判别模型的特征因子。根据因子分析理论及Fisher判别分析理论进行计算和学习。
对30个样本进行因子分析的过程主要分为3个步骤[22]:
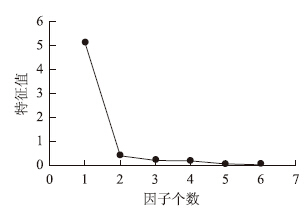
(1)提取公共因子。对样本中相关程度较高的6个变量进行因子分析,运行SPSS17.0软件,得出公共因子碎石图,见图 1。从图 1中可以看出,前2个成分的特征值变化比较明显,特征值从第3个成分开始变化平缓,根据碎石准则,提取前2个成分作为公共因子F1和F2,其累计方差贡献率为92.106%,即可以解释原始变量信息的92.106%。
|
| 图 1 碎石图 Fig. 1Curve of gravel |
(2)构造因子变量。公共因子个数确定后,采用方差最大正交旋转方法对因子载荷矩阵旋转,可以得到因子载荷矩阵,如表 2所示。正交旋转的目的是为了更好地确定公共因子的实际意义。从表 2可知,公共因子F1解释了岩石质量指标、完整性指数、纵波波速3个指标,同时,碎石图中公共因子F1的特征值最为明显,说明其在判别围岩类别中起到重要的作用。同样可以确定,公共因子F2解释了另外3个指标,即饱和单轴抗压强度、弹性抗力系数和结构面摩擦系数。
| 主成分 |
岩石质 量指标 |
完整性 指数 |
饱和单轴 抗压强度 |
纵波 波速 |
弹性抗力 系数 |
结构面 摩擦系数 |
| F1 | 0.891 | 0.771 | 0.421 | 0.785 | 0.440 | 0.656 |
| F2 | 0.345 | 0.557 | 0.872 | 0.571 | 0.876 | 0.662 |
(3)计算因子得分。采用回归方法得出因子得分系数矩阵(见表 3),根据得分系数矩阵可以写出因子得分计算公式如下:
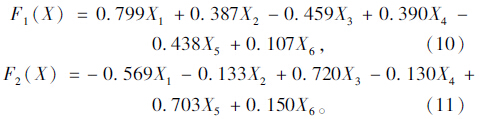
| 主成分 |
岩石质 量指标 |
完整性 指数 |
饱和单轴 抗压强度 |
纵波 波速 |
弹性抗力 系数 |
结构面 摩擦系数 |
| F1 | 0.799 | 0.387 | -0.459 | 0.390 | -0.438 | 0.107 |
| F2 | -0.569 | -0.133 | 0.720 | -0.130 | 0.703 | 0.150 |
根据式(10)和式(11)计算出公共因子F1与F2具体得分,并列入表 1中。
将因子分析后得到的两个公共因子F1和F2作为Fisher判别分析模型的判别因子。应用上述理论,可以得到Fisher判别函数为:
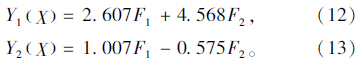
在Fisher判别分析中,判别函数的方差所占的比例体现了判别函数的解释,见表 4。从表 4可以看出,所得到的两个判别函数的判别能力是显著的。第1个判别函数的方差贡献率为98.4%,其判别效率较高,可以解释样本98.4%的信息,其正则相关系数是0.984,使用一次函数可以完成绝大部分样本的判别,但并不能完成全部样本的判别。运用2个判别函数来对样本进行判别,可以使得累计方差贡献率达到100%,即可以解释样本全部信息,因此,利用2个判别函数能够进行更准确的判别。表 4中的组中心值表示各个判别函数在各组别中的中心值。以第1个判别函数为例,其在第Ⅱ类围岩的中心得分为7.604,在Ⅲ类围岩的中心得分为1.473,在Ⅳ类围岩的中心得分为-3.356,在Ⅴ类围岩的中心得分为-6.607。同理可知第2个判别函数在4类围岩中的中心得分。以此为基础,结合Fisher判别分析的计算理论,通过比较待判岩体的函数值与此4类围岩类别的中心值的距离就可以对新样本的围岩类别进行判别。
| 函数 | 特征值 |
方差贡 献率/% |
累计方差 贡献率/% |
正则 相关性 | 组中心值 | |||
| Ⅱ | Ⅲ | Ⅳ | Ⅴ | |||||
| 1 | 29.855 | 98.4 | 98.4 | 0.984 | 7.604 | 1.473 | -3.356 | -6.607 |
| 2 | 0.499 8 | 1.6 | 100.0 | 0.577 | -0.470 | 0.384 | 0.724 | -0.993 |
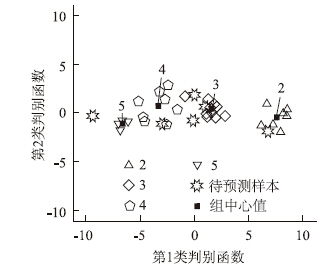
为了检验建立的基于因子分析的Fisher判别分析模型的有效性,采用回代估计法计算误判率,将30个建模样本的数据代入到Fisher判别分析模型中,得到的分类结果列入表 1,可以看出,只有样本8与实际出现偏差,判别的正确率为96.7%。而传统Fisher围岩判别模型[20]回判结果中误判样本有2个,其序号为8和23,判别正确率为93.3%。因此,可认为基于因子分析的Fisher判别分析模型的正确率较高,比较可靠,可以运用到实际的工程项目中。此外,从判别函数分组图(图 2)可观察到,误判样本8介于类别3和类别4之间,比较容易发生误判。分析其原因可能是:(1)个别不同岩体类别的样本在岩性上比较相近,有较强的关联性;(2)训练样本数据有限,所得到的训练函数精度还不够高。
|
| 图 2 判别函数分组图 Fig. 2Grouping figure of discriminant functions |
根据学习好的因子分析与Fisher判别模型对文献[18]中的走马岗隧洞中6个不同桩段的围岩类别进行判别,其具体岩性和指标数据如表 5所示。结合式(10)和(11)计算其公共因子F1和F2的因子得分,将其结果列入表 5中,并将得到的数值代入判别函数Y1(X)(式(12))中,得到6个不同围岩的Fisher函数得分值,见表 6。根据Fisher判别理论,计算各个围岩得分到各类别的中心值的距离D。距离D的计算公式可表示为:距离D=各类别中心值-各围岩Fisher函数得分。以第1个围岩为例,可计算得D2为6.478,D3为0.347,D4为4.482,D5为7.733。由于它与第3类围岩的中心点的距离D3最小,则可以判别第1个围岩属于第3类。同理,可对其他围岩的类别进行判别,其判别结果见表 6,同时与神经网络模型[18]、Bayes方法[10]相比较。可见,3种方法的预测结果一致,与实际类别也完全相符,正确率为100%。神经网络方法有较强的自学习功能,预测精度较高,但需要专业的技术人员进行操作才会得到理想效果。而Bayes模型在应用过程中处理指标个数较多时效率较低。由此可见,基于因子分析的Fisher判别模型预测隧洞围岩的类别是完全可行和高效的。
| 序号 | 围岩岩性描述 | 评价指标实测值 | F1 | F2 | |||||
| X1 | X2 | X3 | X4 | X5 | X6 | ||||
| 1 | 洞身为微风化千枚岩,洞顶为弱风化和微风化岩 | 75 | 0.57 | 82.9 | 4 145 | 10 | 4 | 0.589 08 | -0.089 70 |
| 2 | 洞顶为微风化千枚岩,岩石坚硬,裂隙稍发育 | 80 | 0.69 | 60 | 4 567 | 10 | 4 | 1.491 81 | -0.831 89 |
| 3 | 微风化花岗斑岩,岩石坚硬完整,洞顶微风化和弱风化 | 68 | 0.52 | 120 | 3 980 | 18 | 5.5 | -0.740 65 | 1.913 46 |
| 4 | 弱风化花岗斑岩,岩石坚硬,裂隙发育,完整性较差 | 42 | 0.45 | 62.4 | 3 681 | 10 | 4 | -0.552 39 | 0.310 13 |
| 5 | 弱风化花岗斑岩,岩石坚硬,裂隙发育,完整性较差 | 25 | 0.36 | 62.4 | 3 300 | 3.5 | 3 | -1.035 40 | -0.014 99 |
| 6 | 洞身为弱风化和强风化花岗斑岩,洞顶强风化岩为主 | 25 | 0.17 | 6.3 | 2 300 | 1 | 0.75 | -1.120 81 | -1.395 81 |
| 序号 |
Fisher 函数 得分值 | D2 | D3 | D4 | D5 | 判别结果 | |||
| 本文方法 | 实际类别 | 神经网络 | Bayes方法 | ||||||
| 1 | 1.126 | 6.478 | 0.347 | 4.482 | 7.733 | 3 | 3 | 3 | 3 |
| 2 | 0.089 | 7.515 | 1.384 | 3.445 | 6.696 | 3 | 3 | 3 | 3 |
| 3 | 6.81 | 0.794 | 5.337 | 10.166 | 13.417 | 2 | 2 | 2 | 2 |
| 4 | -0.023 | 7.627 | 1.496 | 3.333 | 6.584 | 3 | 3 | 3 | 3 |
| 5 | -2.768 | 10.372 | 4.241 | 0.588 | 3.839 | 4 | 4 | 4 | 4 |
| 6 | -9.298 | 16.902 | 10.771 | 5.942 | 2.691 | 5 | 5 | 5 | 5 |
以上的研究表明,基于因子分析的Fisher判别模型的预测能力较强,科学合理,性能可靠,为隧洞围岩的分类预测提供了一条数学化、定量化的新途径。
(1)应用因子分析理论研究隧洞围岩分类的指标,对各个指标的相关性进行分析,避免了信息之间的重合,简化了Fisher判别分析过程的工作量。同时,经过因子分析得到岩石质量指标、完整性指数和纵波波速这3个指标对于识别隧洞围岩的类别重要性较大。
(2)利用对样本中相关性强的指标进行因子分析得到的公共因子F1和F2,建立Fisher判别模型,对隧洞围岩的类别进行判别,预测结果与实际类别完全相符,具有较强的适用性。
(3)基于因子分析的Fisher预测模型以有限的勘测数据为基础,学习样本的数量、代表性和正确性对判别结果的准确性有着直接的影响,对分界点附近的样本判别能力也比较有限。在以后的研究中,要广泛收集工程实例资料,选取合适数量的训练样本,提高其代表性和正确性,以提高隧洞围岩分类模型的判别精度。
| [1] | 李之达,黄彬,王花平,等.公路隧道初期支护结构与围岩特性分析[J].武汉理工大学学报:交通科学与工程版,2011,35(2):219-222. LI Zhi-da,HUANG Bin,WANG Hua-ping,et al.Highway Tunnel Primary Support Structure and Surrounding Rock Characteristic Analysis[J].Journal of Wuhan University of Technology:Transportation Science and Engineering Edition,2011,35(2):219-222. |
| [2] | BARTON N.Rock Mass Classification and Tunnel Reinforcement Selection Using the Q-system [C]// Symposium on Rock Classification Systems for Engineering Purposes. Cincinnati, Ohio:American Society for testing and Materials,1988:59-88. |
| [3] | BIENIAWSKI Z T.Engineering Rock Mass Classification a Complete Manual for Engineers and Geologists in Mining,Civil and Petroleum Engineering[M].Wiley:Interscience Publication,1989. |
| [4] | 陈秋南.隧道工程[M].北京:机械工业出版社,2005. CHEN Qiu-nan.Tunnel Engineering[M].Beijing:Mechanical Industry Press,2005. |
| [5] | 郑俊杰,林池峰,赵冬安,等.基于模糊故障树的盾构隧道施工成本风险评估[J].岩土工程学报,2011,33(4):501-508. ZHENG Jun-jie,LIN Chi-feng,ZHAO Dong-an,et al.Shield Tunnel Construction Cost Risk Assessment Based on the Fuzzy Fault Tree[J].Chinese Journal of Geotechnical Engineering,2011,33(4):501-508. |
| [6] | 王晓睿,王元汉,张世海.模糊推理的综合评判系统在隧道围岩智能分类中的应用研究[J].公路交通科技,2009,26(3):100-104. WANG Xiao-rui,WANG Yuan-han,ZHANG Shi-hai.Study on Synthetic Judge System of Fuzzy Reasoning Applied to Intellectual Classification of Tunnel Surrounding Rock [J].Journal of Highway and Transportation Research and Development,2009,26(3):100-104. |
| [7] | 段林娣,宋成辉.应用BP神经网络进行隧道围岩快速分级[J].中国安全科学学报,2010,20(2):41-45,177. DUAN Lin-di,SONG Cheng-hui.Application of BP Neural Network in the Rapid Classification of Surrounding Rock[J].China Safety Science Journal,2010,20(2):41-45,177. |
| [8] | 范加冬,韩立军.基于岭回归-马氏距离的隧道围岩分类预测方法的研究[J].武汉理工大学学报:交通科学与工程版,2014,38(1):199-203. FAN Jia-dong,HAN Li-jun.Classification of Surrounding Rock Based on Methods of Ridge Regression and Mahalanobis Distance Criterion[J].Journal of Wuhan University of Science and Technology: Transportation Science and Engineering Edition,2014,38(1):199-203. |
| [9] | 李晓静,朱维申,陈卫忠,等.层次分析法确定影响地下洞室围岩稳定性各因素的权值[J].岩石力学与工程学报,2004,23(增2):4731-4734. LI Xiao-jing,ZHU Wei-shen,CHEN Wei-zhong,et al.Determining Weight of Factors in Stability Analysis of Underground Caverns by Analytic Hierarchy Process [J].Chinese Journal of Rock Mechanics and Engineering,2004,23(S2):4731-4734. |
| [10] | 文畅平.岩体质量分级的Bayes判别分析方法[J].煤炭学报,2008,33(4):395-399. WEN Chang-ping.Bayes Discriminant Analysis Method of Rock-mass Quality Classification[J].Journal of China Coal Society,2008,33(4):395-399. |
| [11] | 王迎超,孙红月,尚岳全,等.基于特尔菲-理想点法的隧道围岩分类研究[J].岩土工程学报,2010,32(4):651-656. WANG Ying-chao,SUN Hong-yue,SHANG Yue-quan,et al.Classification of Tunnel Surrounding Rock Based on Delphi-ideal Point Method[J].Chinese Journal of Geotechnical Engineering,2010,32(4):651-656. |
| [12] | 苏永华,马宁,胡检.采用小样本统计理论的隧道围岩分类[J].公路交通科技,2010,27(8):66-69,80. SU Yong-hua,MA Ning,HU Jian.Classification of Tunnel Surrounding Rock Based on Small Sample Statistical Theory[J].Journal of Highway and Transportation Research and Development,2010,27(8):66-69,80. |
| [13] | 余伟健,高谦,韩阳,等.非线性耦合围岩分类技术及其在金川矿区的应用[J].岩土工程学报,2008,30(5):663-669. YU Wei-jian,GAO Qian,HAN Yang,et al.Non-linear Coupling Classification Technique of Surrounding Rock Mass and Its Application in Jingchuan Mine[J].Chinese Journal of Geotechnical Engineering,2008,30(5):663-669. |
| [14] | 马庆国.管理统计[M].北京:科学出版社,2008:308-335. MA Qing-guo.Statistics for Managers[M].Beijing:Science Press,2008:308-335. |
| [15] | 李卫东.应用多元统计分析[M].北京:北京大学出版社,2008:342-368. LI Wei-dong.Applied Multivariate Statistics Analysis[M].Beijing:Peking University Press,2008:342-368. |
| [16] | 于秀林.多元统计分析[M].北京:中国统计出版社,2002:125-128. YU Xiu-lin.Multivariate Statistical Analysis[M].Beijing:China Statistics Press,2002:125-128. |
| [17] | 周健,史秀志.冲击地压危险性等级预测的Fisher判别分析方法[J].煤炭学报,2010,35(增1):22-27. ZHOU Jian,SHI Xiu-zhi.Fisher Discriminant Analysis Method for Prediction of Classification of Rock Burst Risk[J].Journal of China Coal Society,2010,35(S1):22-27. |
| [18] | 周翠英,张亮,黄显艺.基于改进BP网络算法的隧洞围岩分类[J].地球科学——中国地质大学学报,2005,30(4):480-486. ZHOU Cui-ying,ZHANG Liang,HUANG Xian-yi.Classification of Rocks Surrounding Tunnel Based on Improved BP Network Algorithm[J].Earth Science—Journal of China University of Geosciences,2005,30(4):480-486. |
| [19] | SL279—2001,公路隧道设计规范[S]. SL279—2001,Code For Design of Road Tunnel[S]. |
| [20] | 姜春露,姜振泉,孙强.基于Fisher 判别分析法的隧洞围岩分类[J].煤炭学报,2012,(37)10:1665-1670. JIANG Chun-lu,JIANG Zhen-quan,SUN Qiang.Tunnel Surrounding Rock Classification Based on Fisher Discriminant Analysis[J].Journal of China Coal Society,2012,(37)10:1665-1670. |
| [21] | GB50218—94,工程岩体分级标准[S]. GB50218—94,Standard for Engineering Classification of Rock Mass [S]. |
| [22] | 邵良杉,赵琳琳.露天采矿爆破振动对民房破坏的旋转森林预测模型[J].中国安全科学学报,2013,23(2):58-63. SHAO Liang-shan, ZHAO Lin-lin.Rotation Forest Analysis Model and Its Application to Predicting Residential House's Damage Against Blasting Vibration of Open Pit Mining[J].China Safety Science Journal,2013,23(2):58-63. |
 2015, Vol. 31
2015, Vol. 31
