扩展功能
文章信息
- 蒋田勇, 谢静思
- JIANG Tian-yong, XIE Jing-si
- 高速公路桥梁随机荷载分布特性研究
- Investigation on Distribution Characteristics of Random Loads on Expressway Bridge
- 公路交通科技, 2015, Vol. 31 (7): 76-83
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (7): 76-83
- 10.3969/j.issn.1002-0268.2015.07.013
-
文章历史
- 收稿日期:2014-06-18
2. 湖南城建职业技术学院 建筑工程系, 湖南 湘潭 411100
2. Department of Architectural Engineering, Hunan Urban Construction College, Xiangtan Hunan 411100, China
作用在桥梁上的随机车流荷载是一项相当复杂的随机变化过程,一般要考虑车辆行驶情况、道路通行状况、各地环境经济影响状况等诸多影响因素。近年来,随着我国对公路桥梁运输量的需求不断加大,各地的交通状况都相继出现了各种严重问题。随着大型货车和重型车的不断涌现,大流量、高强度的车辆荷载长期作用,使得现有的公路桥梁不堪重负,使用年限骤降,安全系数降低,甚至影响到桥梁的使用和行车安全。
罗霞、王荣辉等人[1, 2, 3, 4]对混合车流交通流特性分析并建立疲劳荷载车辆模型;蔡家明、金丹等人[5, 6, 7, 8, 9]以随机车流通过桥梁时对桥梁产生的效应对桥梁进行疲劳分析预测;王磊等[10, 11]将不同车辆组成的车队等效成均布荷载,依据中国现有车辆荷载统计数据,建立了既有公路桥梁车辆荷载效应模型;黄杰等人[12, 13, 14, 15, 16]通过将利用正态分布和威布尔分布特征来模拟调查所获得随机车流数据。
以吉茶高速公路的控制性工程矮寨大桥(国内第一座跨越峡谷的大跨径钢桁加劲梁悬索桥)为工程背景,在车辆荷载调查基础上对其进行随机荷载分布特性研究,得出与实测数据较吻合的分布函数类型,为更好地模拟高速公路桥梁随机车流量分布提供理论依据与数据支持。 1 随机荷载分布特征 1.1 正态函数分布
设X~N(μ,σ2),μ,σ2为未知参数,正态分布的密度函数和分布函数分别为:
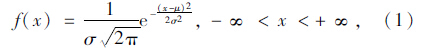
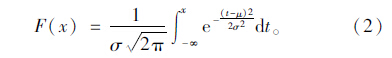
X的概率密度为:
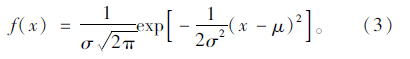
似然函数为:
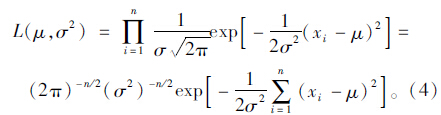
而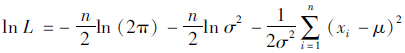 令
令
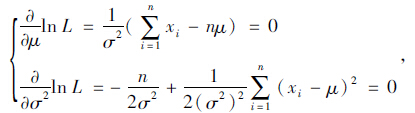
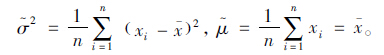
设X~N(μ,σ2),μ,σ2为未知参数,其对数正态分布的密度函数和分布函数分别为:
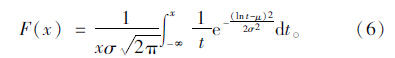
X的概率密度为:

似然函数为:
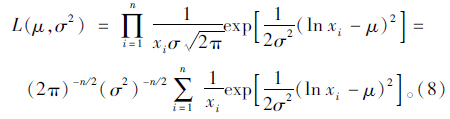
而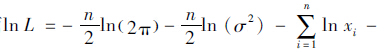
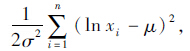 令
令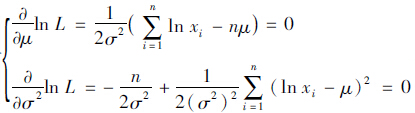 ,
由此可得到最大似然估计量分别为:
,
由此可得到最大似然估计量分别为:
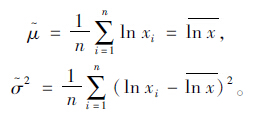
由于威布尔函数分布参数是非线性的,计算时先对分布函数进行二次取对数然后再变量替换,把复杂的参数线性化,最后采用最小二乘法对其参数进行估计。
威布尔分布函数F(t)为:
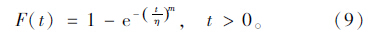
{ti}(i=1,2,…,n)为总体样本,把数据{ti,F(ti)}i=1,2,…,n代入式(9),并对其连续取对数可得:
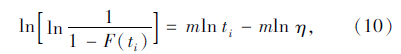
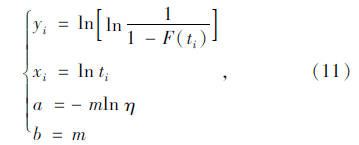
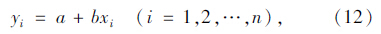
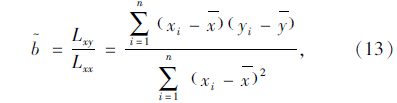

式中
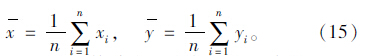
由式(14)可以估计出威布尔分布的参数点:

求解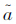 ,
,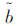 时需要计算
时需要计算 ,而F(t)未知,那么就无法求出F(ti),故此处需要对F(ti)先进行估计,再求出yi,然后才能求出
,而F(t)未知,那么就无法求出F(ti),故此处需要对F(ti)先进行估计,再求出yi,然后才能求出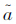 ,
,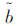 的值。 ti时刻的中位秩MR(ti)作为F(ti)的估计值,
的值。 ti时刻的中位秩MR(ti)作为F(ti)的估计值,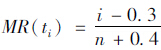 ,F(ti)=MR(ti),然后按上述的方法确定
,F(ti)=MR(ti),然后按上述的方法确定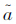 ,
,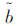 最后求出
最后求出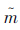 ,
,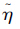 即可。用小二乘估计法对威布尔分布参数进行点估计步骤如下:
即可。用小二乘估计法对威布尔分布参数进行点估计步骤如下:
(1)用频率或中位秩做F(ti)的点估计,记为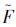 (ti);
(ti);
(2)把样本{ti,F(ti)}(i=1,2,…,n)代入式(9)并连续二次取对数得式(10);
(3)用式(11)作变量替换式(12);
(4)利用最小二乘法得到线性模型式(12)的参数估计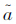 ,
,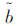 ;
;
(5)把a~,b~代入式(16)后得到威布尔分布的参数估计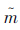 ,
,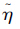 。
。
综上所述,用最小二乘法求威布尔分布的参数估计,简单适用,容易掌握,并采用Mathmatic编制了程序来求解矮寨大桥的荷载调查数据。 1.4 K-S检验
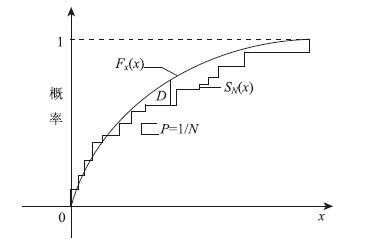
Kolmogorov-Smirnov检验,简称为K-S检验。一般在K-S检验中,先计算需要做比较的两组观察数据的累积分布函数,然后求这两个累积分布函数的差的最大绝对值D,通过查表获得一个置信区间,当D值正好处于置信区间之内,那么认为被检测的数据满足要求,反之亦然。给定一个容量为N的样本,假定样本点服从某分布,则此分布的分布函数为Fx(x)可以根据样本值很快地计算出样本的经验分布函数SN(x),SN(x)曲线呈阶梯状分布,而假定的分布函数曲线Fx(x)为平滑曲线,见图 1。
|
| 图 1 K-S检验方法 Fig. 1K-S test method |
将所有样本点处Fx(x)与SN(x)的最大差值称为K-S检验的统计值D,见式(17)。在SN(x)=0和SN(x)=1处,D=0。
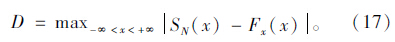
如果对两个不同样本空间的经验分布函数的拟合优度进行检验,则K-S检验的统计量观测值为:
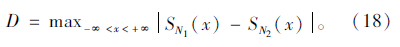
对于给定的显著性水平α,查K-S分布临界值表得到Dn,a。比较统计量观测值D与相应临界值Dn,a。如果D
矮寨大桥车辆荷载调查采用人工调查与仪器观测相结合的方法。其中,测试仪器包括雷达测速仪和录像机。该调查方法能够准确地得到过往车辆的车型、车辆行驶车道、车速及车辆到达时间等数据,并通过调查及查阅相关手册得出相应车辆的轴距、轴重等数据。其中,雷达测速仪是根据接收到的反射波频移量的计算而得出被测物体的运动速度。录像机是用来对过往的车流中的车型、车道及到达时间等分参数进行录像记录。
车重的调查主要是通过高速公路的收费站系统来获取车重。具体方法是,采用摄像机获取通过矮寨大桥的车辆信息,调取高速公路的收费站系统中相应车辆的车重数据,即可完成车重荷载的调查。这种方法的实现主要是由于高速公路的收费站系统在收费车道上安装了高精度动态轴重识别仪。当车轮压过路面时,动态轴重识别仪获取并识别轴轮信号,然后再将信号传入数据转换与处理仪器中,并通过动态数据处理将信号转换为数据,从而计算出各轮轴的轴重以及所有轮轴总重。
矮寨大桥的车辆分为7种类型:第1类为小型面包车,第2类为小轿车,第3类为小型客车,第4类为大型客车,第5类为小型货车,第6类为中型货车,第7类为大型货车。矮寨大桥车辆荷载主要是以第2类小轿车和第7类大型货车为主,其中小轿车占总车辆的49.5%,大型货车占总车辆的21.56%,其余类型车辆所占的比例均小于10%,如图 3所示。本次选取随机车辆的车速和车重两个显著特征值进行分布特性研究。
从表 1可以看出,第1类车型车速在显著水平0.01的情况下,正态分布、对数正态分布和威布尔分布等分布的K-S检验均不能通过。为了能准确地获取矮寨大桥的随机车辆荷载近似函数,对第1类小型面包车的车速进行非线性拟合,结果表明正态分布最接近实测车速的分布特点。因此,第1类车型小型面包车的车速分布可以采用正态分布函数见图 4。 从表 2可以得出,对第2类车型小轿车车速进行显著水平为0.01的正态分布、对数正态分布和威布尔分布拟合,然后再进行K-S检验,结果表明第2类车型小轿车车速分布均不通过K-S检验。从图 5可以看出,第2类车型小轿车的车速分布曲线更加接近正态分布,故第2类车型小轿车的车速分布可以采用正态分布函数。
从表 3和图 6可以得出,在显著性水平为0.01下,第3类车型小型客车的车速分布能够通过正态分布、对数正态分布和威布尔分布的K-S检验。结合图表可以看出,正态分布曲线与实测曲线更接近,故第3类车型小型客车的车速分布可以采用正态分布函数。

图 2 车辆荷载现场调查典型照片
Fig. 2Typical pictures of vehicle load investigation
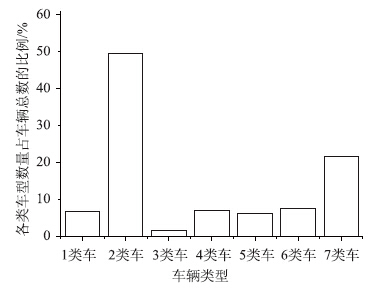
图 3 各车型车辆数所占比例分布图
Fig. 3Proportions of various vehicle types
参数 正态分布 对数正态分布 威布尔分布 分布参数一 μ=76.78 μ=4.33 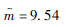
分布参数二 σ=9.58 σ=0.13 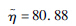
D 0.096 0.118 0.095 Dn,a 0.064 0.064 0.065 K-S检验 不通过 不通过 不通过
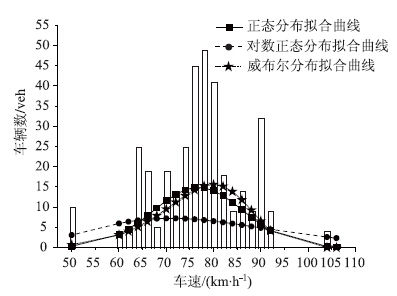
图 4 第1类车型车速分布图
Fig. 4Speed distribution of the first vehicle type
参数 正态分布 对数正态分布 威布尔分布 分布参数一 μ=81.93 μ=4.39 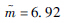
分布参数二 σ=14.88 σ=0.18 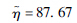
D 0.066 0.062 0.069 Dn,a 0.024 0.024 0.024 K-S检验 不通过 不通过 不通过
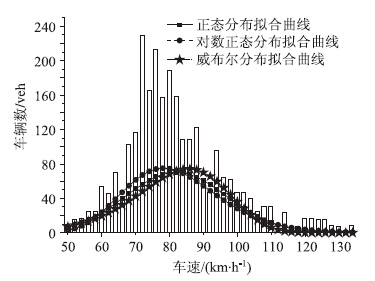
图 5 第2类车型的车速分布图
Fig. 5Speed distribution model of the 2nd vehicle type
参数 正态分布 对数正态分布 威布尔分布 分布参数一 μ=67.56 μ=4.21 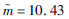
分布参数二 σ=7.58 σ=0.11 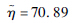
D 0.126 0.079 0.089 Dn,a 0.131 0.131 0.131 K-S检验 通过 通过 通过
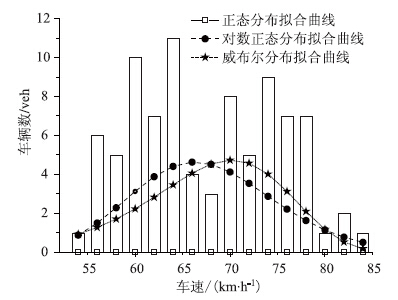
图 6 第3类车型车速分布图
Fig. 6Speed distribution model of the 3rd vehicle type
| 类型 | 参数 | ||
| 正态分布 | 对数正态分布 | 威布尔分布 | |
| 分布参数一 | μ=75.58 | μ=4.32 | 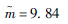 |
| 分布参数二 | σ=10.17 | σ=0.14 | 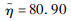 |
| D | 0.063 | 0.063 | 0.066 |
| Dn,a | 0.063 | 0.063 | 0.063 |
| K-S检验 | 通过 | 通过 | 不通过 |
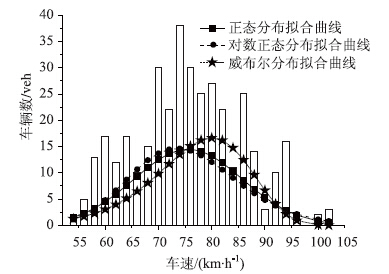
|
| 图 7 第4类车型车速分布图 Fig. 7Speed distribution model of the 4th vehicle type |
从表 5和图 8中可以得出,显著水平为0.01时,对第5类车型小型货车的车速分布曲线进行的正态分布、对数正态分布和威布尔分布拟合,K-S检验结果表明第5类车型小型货车的车速分布能够通过正态分布和对数正态分布。通过对比得出,正态分布曲线与实测曲线更加接近,故第5类车型小型货车的车速分布可以采用正态分布函数。
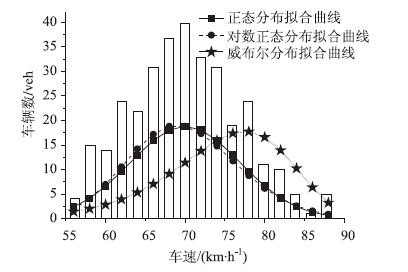
|
| 图 8 第5类车型车速分布图 Fig. 8Speed distribution model of the 5th vehicle type |
| 参数 | 类型 | ||
| 正态分布 | 对数正态分布 | 威布尔分布 | |
| 分布参数一 | μ=70.01 | μ=4.24 | 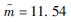 |
| 分布参数二 | σ=6.91 | σ=0.10 | 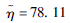 |
| D | 0.065 | 0.065 | 0.088 |
| Dn,a | 0.068 | 0.068 | 0.068 |
| K-S检验 | 通过 | 通过 | 不通过 |
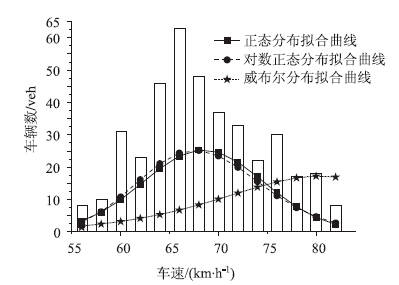
从表 6和图 9可以得出,显著水平为0.01时,对第6类车型中型货车的车速进行正态分布、对数正态分布和威布尔分布拟合,K-S检验结果表明3种分布都不能通过。但通过对比得出,正态分布曲线与实测曲线更加接近,故第6类车型中型货车的车速分布可以采用正态分布函数。
| 参数 | 正态分布 | 对数正态分布 | 威布尔分布 |
| 分布参数一 | μ=68.47 | μ=4.22 | 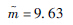 |
| 分布参数二 | σ=6.19 | σ=0.09 | 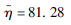 |
| D | 0.100 | 0.098 | 0.143 |
| Dn,a | 0.061 | 0.061 | 0.061 |
| K-S检验 | 不通过 | 不通过 | 不通过 |
|
| 图 9 第6类车型车速分布直方图 Fig. 9Speed distribution model of the 6th vehicle type |
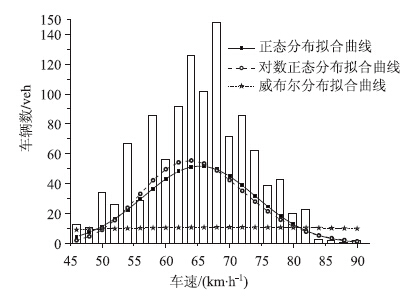
从表 7和图 10可以得出,显著水平为0.01时,对第7类车型大型货车的速度进行正态分布、对数正态分布和威布尔分布拟合,结果表明3种分布都不能通过K-S检验。用正态分布对其进行非线形拟合后,发现其曲线近似度较好,故采用正态分布对第7类车型大型货车的车速分布进行近似替代。
|
| 图 10 第7类车型车速分布图 Fig. 10Speed distribution model of the 7th vehicle type |
| 参数 | 正态分布 | 对数正态分布 | 威布尔分布 |
| 分布参数一 | μ=65.31 | μ=4.17 | 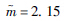 |
| 分布参数二 | σ=8.77 | σ=0.13 | 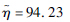 |
| D | 0.086 | 0.087 | 0.120 |
| Dn,a | 0.036 | 0.036 | 0.036 |
| K-S检验 | 不通过 | 不通过 | 不通过 |
通过以上7种类型车速的函数拟合和K-S检验得出,各车型车速大多服从或近似服从正态分布,故各类车型的车速分布采用正态分布函数。
2.3 车重分布特性图 11为各类车型的车重分布图。
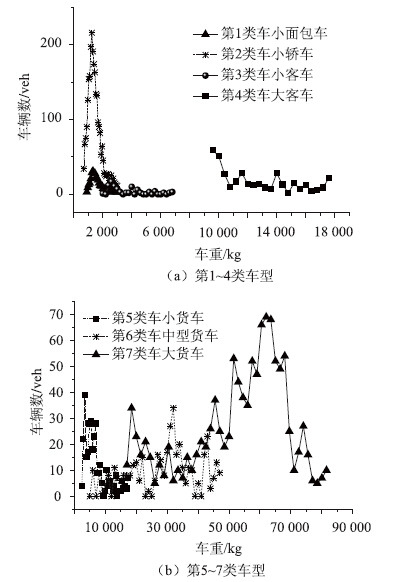
|
| 图 11 各类车型的车重分布图 Fig. 11Weight distribution of various vehicle types |
从表 8~表 14可以得出,在显著性水平为0.01下,对各车型进行车重分布拟合并进行K-S检验,检验结果表明,这7种类型车的车辆均不能满足正态分布,对数正态分布和威布尔分布。但是,各类车重分布类型K-S检验参数表中,正态分布统计量观测值D与相应临界值Dn,a更接近,各车型车重分布可选用正态分布函数。
| 参数 | 正态分布 | 对数正态分布 | 威布尔分布 |
| 分布参数一 | μ=1 646.3 | μ=7.37 | 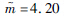 |
| 分布参数二 | σ=491.29 | σ=0.28 | 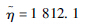 |
| D | 0.083 | 0.084 | 0.084 |
| Dn,a | 0.065 | 0.065 | 0.065 |
| K-S检验 | 不通过 | 不通过 | 不通过 |
| 参数 | 正态分布 | 对数正态分布 | 威布尔分布 |
| 分布参数一 | μ=1 646.3 | μ=7.23 | 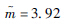 |
| 分布参数二 | σ=475.53 | σ=0.31 | 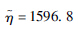 |
| D | 0.082 | 0.082 | 0.081 |
| Dn,a | 0.024 | 0.024 | 0.024 |
| K-S检验 | 不通过 | 不通过 | 不通过 |
| 参数 | 正态分布 | 对数正态分布 | 威布尔分布 |
| 分布参数一 | μ=3 572.4 | μ=8.13 | 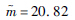 |
| 分布参数二 | σ=1 269.7 | σ=0.32 | 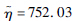 |
| D | 0.175 | 0.195 | 0.195 |
| Dn,a | 0.131 | 0.131 | 0.131 |
| K-S检验 | 不通过 | 不通过 | 不通过 |
| 参数 | 正态分布 | 对数正态分布 | 威布尔分布 |
| 分布参数一 | μ=12 395.6 | μ=9.41 | 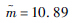 |
| 分布参数二 | σ=2 568.70 | σ=0.20 | 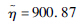 |
| D | 0.130 | 0.161 | 0.161 |
| Dn,a | 0.063 | 0.063 | 0.063 |
| K-S检验 | 不通过 | 不通过 | 不通过 |
| 参数 | 正态分布 | 对数正态分布 | 威布尔分布 |
| 分布参数一 | μ=6 973.85 | μ=8.72 | 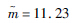 |
| 分布参数二 | σ=3 814.03 | σ=0.50 | 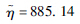 |
| D | 0.120 | 0.120 | 0.121 |
| Dn,a | 0.068 | 0.068 | 0.068 |
| K-S检验 | 不通过 | 不通过 | 不通过 |
| 参数 | 正态分布 | 对数正态分布 | 威布尔分布 |
| 分布参数一 | μ=29 103.81 | μ=10.19 | 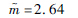 |
| 分布参数二 | σ=10 689.9=σ | 0.47 | 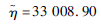 |
| D | 0.086 | 0.086 | 0.086 |
| Dn,a | 0.061 | 0.061 | 0.061 |
| K-S检验 | 不通过 | 不通过 | 不通过 |
| 参数 | 正态分布 | 对数正态分布 | 威布尔分布 |
| 分布参数一 | μ=52 831.6 | μ=10.81 | 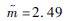 |
| 分布参数二 | σ=15 818.70 | σ=0.38 | 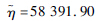 |
| D | 0.060 | 0.060 | 0.060 |
| Dn,a | 0.036 | 0.036 | 0.036 |
| K-S检验 | 不通过 | 不通过 | 不通过 |
采用正态分布、对数正态分布和威布尔分布共3种分布类型函数对吉茶高速公路矮寨大桥车流量进行参数分析和优化拟合,并通过K-S检测方法检验其是否满足要求,寻找出与实测分布最为接近的分布参数及分布类型。
(1)利用最大似然估计法推导了正态分布和对数正态分布函数的分布参数表达式,采用最小二乘法得到威布尔函数的分布参数表达式,并编制了Mathmatic编程来求解荷载调查数据。
(2)根据调查结果和参考车辆技术手册中分类,矮寨大桥的车辆分为7种类型,且主要是以第2类小轿车和第7类大型货车为主,其中小轿车占总车辆的49.5%,大型货车占总车辆的21.56%,其余类型车辆所占的比例均小于10%。
(3)各车型的车速分布特性研究结果表明,第3类、第4类和第5类车型车速K-S检验都满足正态分布;第1类、第2类、第6类和第7类车型的车速K-S检验虽然均不满足正态分布,但这4类车型车速的正态拟合曲线、对数正态拟合曲线和威布尔拟合曲线与实测分布曲线对比,表明正态拟合曲线与实测车速分布特点最接近。由此可见,各车型的车速分布可选用正态分布函数。
(4)对各车型的车重分布研究表明,K-S检验7种车型的车重均不满足正态分布、对数正态分布和威布尔分布,但其正态分布统计量观测值D与相应临界值Dn,a更接近,故各车型车重分布可选用正态分布函数。
| [1] | 罗霞, 杜进有, 陈应文. 混合车流交通流特性分析[J].西南交通大学学报, 2000, 35(3):297-300. LUO Xia, DU Jin-you, CHEN Ying-wen. Analyses on Multi-traffic Flow's Characteristics [J]. Journal of Southwest Jiaotong University, 2000, 35(3): 297-300. |
| [2] | 罗霞, 杜进有, 霍娅敏. 车头间距分布规律的研究[J]. 西南交通大学学报, 2001, 36(2):113-116. LUO Xia, DU Jin-you, HUO Ya-min. Study on the Distribution Patterns of Time Headway of Vehicles[J]. Journal of Southwest Jiaotong University, 2001, 36(2): 113-116. |
| [3] | 王荣辉, 池春, 陈庆中,等. 广州市高架桥疲劳荷载车辆模型研究[J]. 华南理工大学学报:自然科学版, 2004, 32(12):94-96. WANG Rong-hui, CHI Chun, CHEN Qing-zhong, et al. Study on the Model of the Fatigue-loaded Vehicles in Guangzhou Trestle Bridges[J]. Journal of South China University of Technology:Natural Science Edition, 2004, 32(12): 94-96. |
| [4] | 赵琛, 黄培彦, 黄龙田. 桥梁随机载荷数据采集及统计分析[J]. 中南公路工程, 2004, 29(1):12-15. ZHAO Chen, HUANG Pei-yan, HUANG Long-tian. Acquisition and Statistic Analysis of Random Load Data for Bridges[J]. Journal of Central South Highway Engineering, 2004, 29(1):12-15. |
| [5] | 蔡家明. 城市路段车流量分布规律的寻优拟合[J]. 上海工程技术大学学报, 2006, 20(2): 100-103. CAI Jia-ming. Better Fitting for Distribution of Vehicles Flow on Road Segment of City[J]. Journal of Shanghai University of Engineering Science,2006, 20(2): 100-103. |
| [6] | 金丹, 陈旭. 多轴随机载荷下的疲劳寿命估算方法[J]. 力学进展, 2006, 36(1):65-74. JIN Dan, CHEN Xu. Fatigue Life Evaluation under Multiracial Random Loadings[J]. Advances in Mechanics, 2006, 36(1):65-74. |
| [7] | 冯秀峰, 宋玉普, 朱美春. 随机变幅疲劳荷载下预应力混凝土梁疲劳寿命的试验研究[J]. 土木工程学报, 2006, 39(9): 32-38. FENG Xiu-feng, SONG Yu-pu, ZHU Mei-chun. An Experimental Study on the Fatigue Life of Prestressed Concrete Beams under Random-amplitude Fatigue Loading[J]. China Civil Engineering Journal, 2006, 39(9): 32-38. |
| [8] | 赵呈建. 威布尔分布参数估计的研究[D]. 天津:南开大学, 2007. ZHAO Chen-jian. Study of Parameters Estimation Methods for Weibull Distribution[D]. Tianjin: Nankai University, 2007. |
| [9] | 陈照全. 既有桥梁车辆荷载的随机过程模型研究[D]. 长沙:长沙理工大学, 2007. CHEN Zhao-quan. Research on Traffic Load Stochastic Process Model of Existing Bridge [D]. Changsha: Changsha University of Science and Technology, 2007. |
| [10] | 王磊, 张建仁. 基于平衡更新过程的既有桥梁车辆荷载效应模型[J]. 中国公路学报, 2008, 21(5):50-56. WANG Lei, ZHANG Jian-ren. Vehicle Load Effect Model for Existing Bridge Based on Equilibrium Renewal Process[J]. China Journal of Highway and Transport, 2008, 21 (5): 50-60. |
| [11] | 王磊, 张建仁. 既有公路桥梁不同车辆荷载连续到达过程模拟[J]. 中外公路, 2008, 28(2):83-88. WANG Lei, ZHANG Jian-ren. Continuous Reach Process Simulation of Different Vehicle Loads on Existing Road Bridge [J]. Journal of China and Foreign Highway, 2008, 28(2): 83-88. |
| [12] | 黄杰. 模拟服从正态分布随机变量的方法及应用[D]. 武汉:华中科技大学, 2009. HUAN Jie. A Method of Simulating Random Variables Normal Distribution and Its Application[D]. Wuhan: Huazhong University of Science and Technology, 2009. |
| [13] | 游达章. 最小二乘法在威布尔分布的可靠性评估[J]. 湖北工业大学学报, 2009, 24(4):34-45. YOU Da-zhang. The Application and Arithmetic of the Least Square Method in the Reliability Assessment Based on Weibull Distribution[J]. Journal of Hubei University of Technology, 2009, 24(4):34-45. |
| [14] | 周泳涛, 鲍卫刚, 翟辉. 我国高速公路交通荷载标准研究[J]. 公路交通科技, 2010, 27(2):36-41. ZHOU Yong-tao, BAO Wei-gang, ZHAI Hui. Research on Standard Traffic Load for Expressway [J]. Journal of Highway and Transportation Research and Development, 2010, 27(2): 36-41. |
| [15] | 王涛. 高速公路桥梁交通荷载调查分析及仿真模拟[D].长安:长安大学, 2010. WANG Tao. Investigation and Simulation for Traffic Loading on Expressway Bridge[D]. Chang'an:Chang'an University, 2010. |
| [16] | 金良琼. 两参数Weibull分布的参数估计[D]. 昆明:云南大学, 2010. JIN Liang-qiong. Parameter Estimation of Two-parameter Weibull Distribution[D]. Kunming: Yunnan University, 2010. |
 2015, Vol. 31
2015, Vol. 31
