扩展功能
文章信息
- 陈水生, 田正龙, 桂水荣
- CHEN Shui-sheng, TIAN Zheng-long, GUI Shui-rong
- 单箱多室波形钢腹板箱梁剪力滞研究
- Research on Shear Lag of Single-box Multi-cell Girder with Corrugated Steel Webs
- 公路交通科技, 2015, Vol. 31 (7): 69-75
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (7): 69-75
- 10.3969/j.issn.1002-0268.2015.07.012
-
文章历史
- 收稿日期:2014-07-18
箱形截面由于抗扭刚度大和结构稳定性好而被广泛关注,但初等梁理论不适用于薄壁箱梁,造成其应力分布有所不同。由于薄壁箱梁中沿梁宽方向上顶底板剪切变形的非均匀分布,引起梁体弯曲时离腹板较远位置的纵向位移,滞后于腹板附近的混凝土板的纵向位移,从而导致箱梁弯曲应力沿梁宽方向的分布呈曲线形状,这种弯曲应力沿梁宽方向的不均匀分布现象就是剪力滞效应。当箱梁顶板或者底板与腹板连接处的正应力大于沿板宽其余各点处正应力时的剪力滞称为正剪力滞;反之为负剪力滞[1]。目前,国内外学者对薄壁箱梁剪力滞问题研究形成了如弹性理论解法[2, 3]、比拟杆法[4]、能量变分法[5]等多种理论和方法,并取得不少研究成果。郭金琼[6]、张士铎[7]用变分法研究对称带悬臂的单室箱梁,认为三次抛物线符合实际剪力滞效应的翘曲位移函数;罗旗帜、吴幼明[8, 9]将能量变分法与有限元法结合,扩宽了能量变分法的应用范围;钱寅泉[10]用余弦级数构造了单室箱梁的翘曲位移函数,并将其应用到简支箱梁;韦成龙[11]构造的多参数翘曲位移更具有一般性,适用更加广泛;李立峰[12]、郑尚敏[13]对钢-混凝土组合结构的剪力滞效应进行了较为深入的研究。
波形钢腹板组合箱梁是用波形钢腹板代替混凝土腹板形成的一种钢-混凝土组合梁,在这种结构中钢腹板承担大部分剪力,混凝土顶底板承担大部分弯矩。与混凝土箱梁相同,波形钢腹板组合箱梁也存在弯曲应力沿翼缘板宽度范围分布不均匀的剪力滞效应。以往剪力滞效应的研究对象大多是单箱单室混凝土箱形截面,对单箱多室箱形截面的分析研究较少,对单箱多室波形钢腹板箱梁剪力滞效应的研究更少。
本文采用能量变分法,通过引入剪滞翘曲位移函数,建立了考虑剪切变形影响的波形钢腹板箱梁截面横向位移分布模式,并对悬臂板和底板的翘曲位移函数引入合适的修正系数,以近似考虑其翘曲变形的差异,利用平衡条件建立了多室波形钢腹板箱梁考虑剪力滞效应的控制微分方程,并结合实际桥梁分析了剪力滞系数在不同条件下的分布规律。 1 多室波形钢腹板箱梁剪力滞翘曲位移模式
在应用能量变分原理分析图 1所示的单箱两室或单箱三室波形钢腹板箱梁的弯曲时,引入两个广义位移的概念,即梁的竖向挠度ω(x)与纵向位移u(x,y,z)。
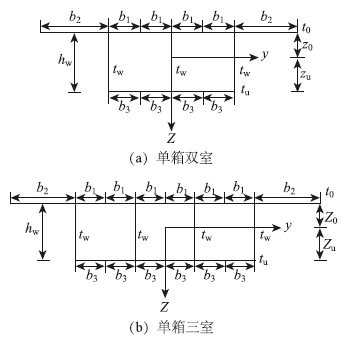
|
| 图 1 单箱双室和单箱三室箱梁横截面图 Fig. 1Cross-section of single-box twin-cell and single-box triple-cell box girders |
横截面上任意一点的纵向位移u(x,y,z)可表示为[14, 15]:
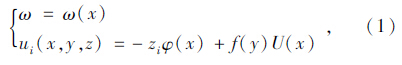
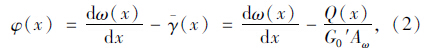
单箱两室波形钢腹板箱梁截面,剪力滞翘曲位移函数f(y)可表示为:
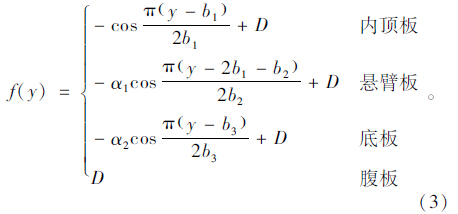
单箱三室波形钢腹板箱梁截面,剪力滞翘曲位移函数f(y)可表示为:

式中,D为满足全截面的轴力自平衡的附加轴向位移;b1,b3分别为单个箱室顶板、底板宽度的一半,b2为箱梁一侧的翼缘板宽度。根据截面轴力为零的平衡条件∫A f(y)dA=0,得到:


式中,A1~A5分别为内顶板、内底板、外伸悬臂板、外顶板、外底板的面积;αi(i=1,2,3,4,5,6)分别为[14]:
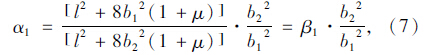
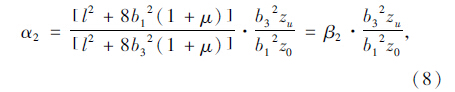

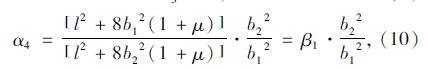
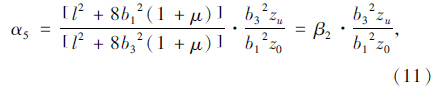
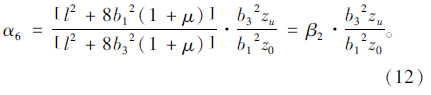
对于单箱双室波形钢腹板箱梁截面,外力势能[15]:
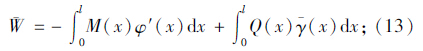
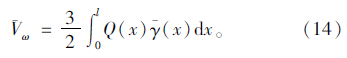
计算顶底板的应变能时,采用近似的方法,将顶底板按照面积相等的原理,保持箱梁的宽度不变改变其厚度,使其变为等厚度截面。
顶底板的应变能:
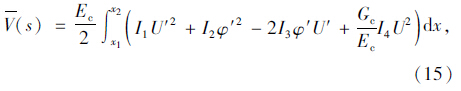
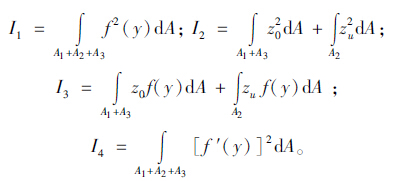
则体系的总势能为:
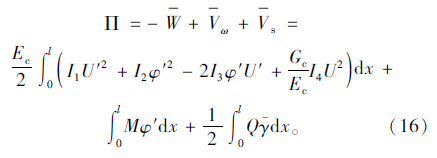
令: 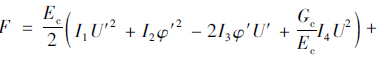
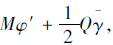 由边界条件,可得:
由边界条件,可得:
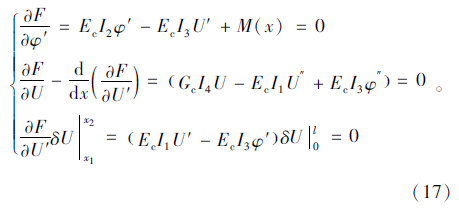
由(17)可得剪力滞微分方程:
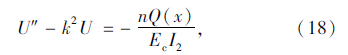
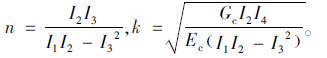
式(18)微分方程解的一般形式为:
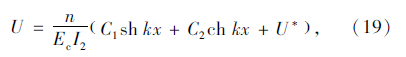
结合式(1)和式(17)的第一个边界条件,得到弯曲正应力:
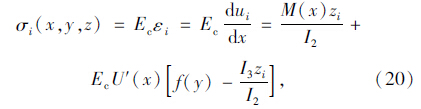
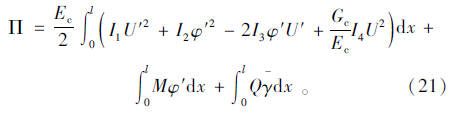
结合简支箱梁的边界条件,依据文献[15],推导了单箱多室波形钢腹板简支箱梁在跨中集中力和满跨均布荷载作用下的弯曲正应力和剪力滞系数。
等截面简支箱梁在跨中作用集中荷载P时,跨中截面正应力:
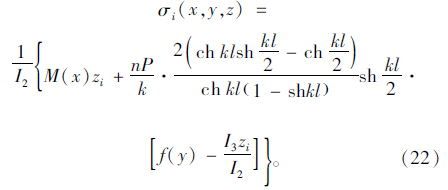
跨中截面剪力滞系数:
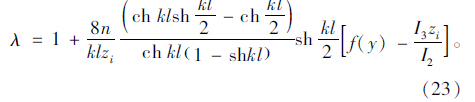
同理,简支箱梁在均布荷载q作用时,得到跨中截面正应力:
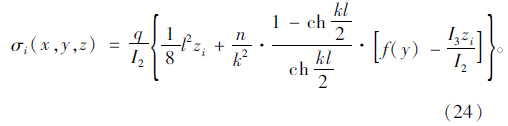
跨中截面剪力滞系数:
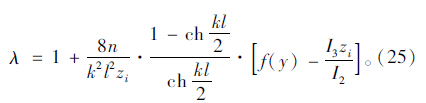
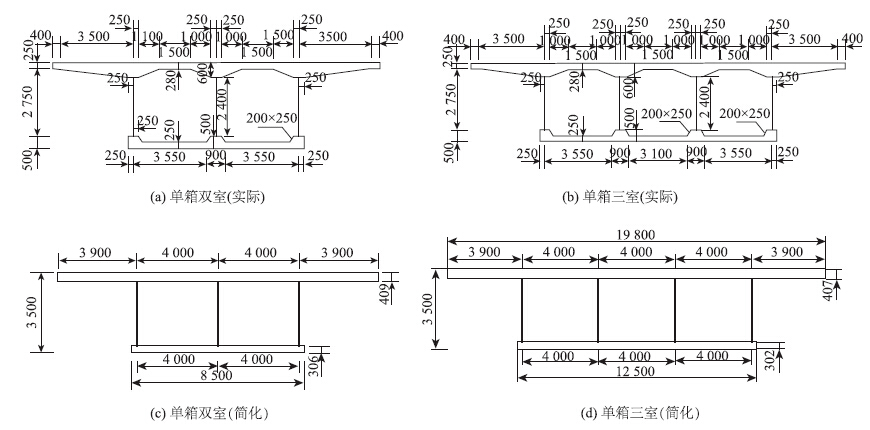
以南昌市朝阳大桥不等跨箱梁桥为例,该桥为单箱多室的波形钢腹板连续箱梁桥,取跨径为50 m的单箱双室和单箱三室的节段各一跨分别进行研究。为方便理论公式的计算和精确度考虑,按照箱梁顶底板截面面积相等的原则,将其等效为矩形截面,作为单箱多室波形钢腹板等截面简支箱梁进行分析。实际与简化模型的结构尺寸如图 2所示,混凝土材料的弹性模量为34.5 GPa,泊松比为0.167,波形钢腹板的弹性模量为206 GPa,泊松比为0.283,箱梁端部现浇混凝土部分为1.25 m,与波形钢腹板连接的混凝土实腹段为3.5 m,分别在跨中作用P=90 kN 的集中荷载和q=30 kN/m的均布荷载。为了比较本文提出的理论公式的可靠性,使用Ansys空间有限元分析软件建立了相应的有限元数值模型,其中混凝土部分采用solid65号各向异性的三维实体单元,波形钢腹板部分采用shell63号四边形壳体单元。荷载在横截面均作用在腹板对应的箱梁顶板部位,如图 3、图 4所示。
|
| 图 2 实桥横截面实际与简化模型具体尺寸图(单位:mm) Fig. 2Dimensions of cross-sections of real bridge and simplified bridge model (unit:mm) |
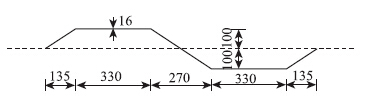
|
| 图 3 波形钢腹板的具体尺寸(单位:mm) Fig. 3Dimensions of corrugated steel web (the unit:mm) |

|
| 图 4 Ansys箱梁模型 Fig. 4Ansys box girder model |
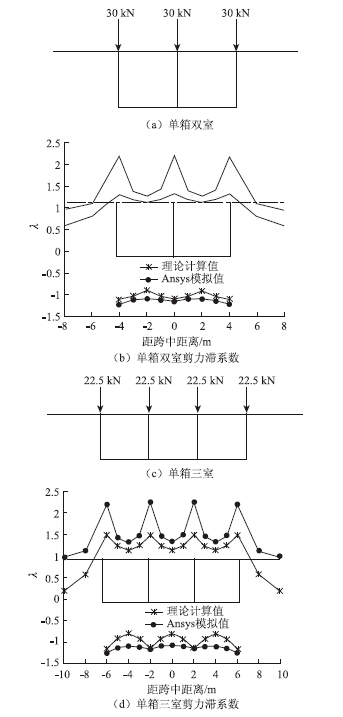
简支梁作为最简单的结构体系,当在跨中集中荷载和满跨均布荷载作用时,跨中是应力和变形较大的部位,其弯矩分别为1/4Pl和1/8ql2;利用本文解析解和Ansys有限元模型得到单箱双室和三室波形钢腹板箱梁跨中截面的剪力滞系数,如图 5、图 6所示。
|
| 图 5 集中荷载作用时的跨中剪力滞系数 Fig. 5Shear lag coefficients of mid-span under concentrated load |
|
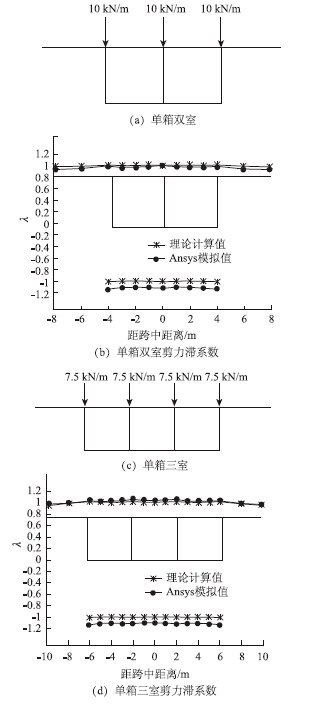
| 图 6 均布荷载作用时的跨中剪力滞系数 Fig. 6Shear lag coefficients of mid-span under uniformly distributed load |
从图 5、图 6的箱梁横截面剪力滞系数分布规律得出,单箱双室和三室波形钢腹板简支箱梁在跨中集中力和均布荷载作用下均表现为明显的正剪力滞现象,腹板与顶底板交接处的剪力滞系数最大,随着离开腹板距离的增大而减小。
由图 5可知,集中荷载作用下本文计算值小于Ansys软件模拟值,大部分区域Ansys模拟结果约为本文解的1.2倍,但是两者在腹板与顶底板交接处和外伸悬臂板边缘处的剪力滞系数结果偏差较大,在腹板与顶底板交接处Ansys模拟结果约为本文解的1.8倍,而外伸悬臂板边缘处Ansys模拟结果约为本文解的2~4倍。由图 6可以看出,均布荷载作用下本文值与Ansys模拟值的吻合程度较好,在顶板处两者趋于一致,而在底板处两者符合集中荷载作用时的关系式:Ansys模拟值约为本文解的1.2倍。进一步分析计算值与模拟值不一致的原因可能有:本文的解析解是从考虑简支梁承受均布荷载的角度出发,因而在集中荷载作用下可能造成一定的偏差;其次,波形钢腹板箱梁与混凝土箱梁的性质方面存在一定的差异,腹板与顶底板相交部位可能造成更大的应力集中现象;最后,计算假设与简化和实际情况相比,存在一定的差异,且计算中没有考虑波形钢腹板承担的正应力。 4.3 剪力滞系数与箱梁跨宽比的关系
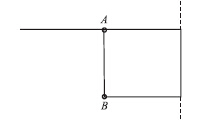
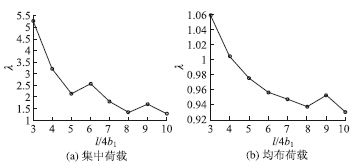
以单箱双室箱梁截面为例,选取跨中箱梁截面两个代表性的点(如图 7所示)来研究单箱多室波形钢腹板简支箱梁剪力滞系数随跨宽比(l/4b1)变化的规律;控制b1=2 m,改变桥梁的跨径,得出不同跨宽比情况下A、B两点的剪力滞系数,结果如图 8、图 9所示。
|
| 图 7 单箱双室波形钢腹板箱梁截面选点图 Fig. 7Cross-section points of single-box twin-cell box girder with corrugated steel webs |
|
| 图 8 点在集中荷载和均布荷载作用下剪力滞系数变化图 Fig. 8Curves of shear lag coefficient under concentrated load and uniformly distributed load at point A |
|
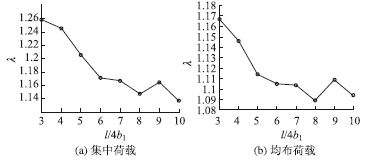
| 图 9 点在集中荷载和均布荷载作用下剪力滞系数变化图 Fig. 9Curves of shear lag coefficient under concentrated load and uniformly distributed load at point B |
由图 8、图 9可以看出,A、B两点的跨中剪力滞系数均随着跨宽比的增大而逐渐减小,剪力滞现象越来越不明显;在集中荷载作用下的剪力滞系数要大于相对应的均布荷载作用下的剪力滞系数;集中荷载作用下的曲线在A点的下降值更加明显,总体下降了4左右,而B点下降了0.12左右;均布荷载作用下曲线在B点的幅值要略大于在A点的幅值。应该指出的是,当跨宽比等于9时,跨中剪力滞系数并不单调下降。 5 结论
本文通过建立考虑剪切变形影响的单箱多室波形钢腹板箱梁的剪力滞控制微分方程,得到了考虑剪力滞效应的弯曲正应力和剪力滞系数表达式,结合ANSYS数值模拟分析了单箱多室波形钢腹板简支箱梁在跨中集中荷载和均布荷载作用下的分布规律,得到如下结论:
(1)本文推导的剪力滞系数解析解能够反映单箱多室波形钢腹板箱梁的剪力滞翘曲差异,在均布荷载作用下的剪力滞系数分布吻合较好,集中荷载作用下的剪力滞系数与有限元结果偏差较大,可引入修正系数1.2对结果进行调整,得到较为精确的结果;本文提出的解对实际波形钢腹板箱梁桥剪力滞系数的取值具有参考价值。
(2)在不同的加载方式下得到的剪力滞系数不同,当多室波形钢腹板箱梁承受跨中集中荷载作用时,腹板与顶底板交接处的剪力滞系数尤为突出,实际桥梁中,应重点考虑此部位的弯曲与开裂情况。
(3)单箱多室波形钢腹板等截面简支箱梁的跨中剪力滞系数随跨宽比的增大而减小。
(4)针对单箱多室波形钢腹板箱梁在腹板与顶底板接合处剪力滞系数较为突出的现象,应对此位置附近进行钢筋加密、相交部位的截面尺寸调整等措施,以减小弯曲应力;波形钢腹板箱梁桥设计时,应选择合适的跨宽比,保持跨中剪力滞系数在适中范围内,避免桥梁的失稳和局部破坏。
| [1] | 郭金琼,房贞政,郑振.箱形梁设计理论 [M]. 2版.北京:人民交通出版社,2008. GUO Jin-qiong, FANG Zhen-zheng, ZHENG Zhen. Design Theory of Box Girder [M]. 2nd ed. Beijing: China Communications Press, 2008. |
| [2] | ABDEL-SAYED G. Effective Width of Steel Deck Plate in Bridges [J]. Journal of Structural Division, 1969, 95(ST7):1459-1474. |
| [3] | MALCOLM D J, REDWOOD R G. Shear Lag in Stiffened Box Girders [J]. Journal of Structural Division, 1970, 96(ST7):1403-1415. |
| [4] | 程翔云,汤康恩. 计算箱形梁桥剪力滞效应的比拟杆法 [J].公路工程,1984(1):65-73. CHENG Xiang-yun, TANG Kang-en. Bar Simulation Method for Calculating Shear Lag Effect in Box Girder [J]. Highway Engineering, 1984(1):65-73. |
| [5] | REISSNER E. Analysis of Shear Lag in Box Beams by the Principle of Minimum Potential Energy [J]. Quarterly of Applied Mathematics,1946,5(3):268-278. |
| [6] | 郭金琼,房贞政,罗孝登. 箱形梁桥剪滞效应分析 [J]. 土木工程学报,1983,16(1):1-13. GUO Jin-qiong, FANG Zhen-zheng, LUO Xiao-deng. Analysis of Shear Lag Effect in Box Girder Bridges [J]. China Civil Engineering Journal, 1983,16(1):1-13. |
| [7] | 张士铎,谢琪. 二次抛物线变截面悬臂梁剪力滞效应及差分解 [J]. 结构工程师,1987(1):35-40. ZHANG Shi-duo, XIE Qi. Shear Lag Effect and Finite Difference Method of Quadratic Parabolic Variable Cross-section Cantilever Beam [J]. Structural Engineers, 1987(1):35-40. |
| [8] | 罗旗帜. 薄壁箱形梁剪力滞计算的梁段有限元法 [J]. 湖南大学学报,1991(2):95-102. LUO Qi-zhi. Calculation of Shear Lag in Thin Walled Box Girders by Finite Segment Method [J]. Journal of Hunan University, 1991(2):95-102. |
| [9] | 吴幼明,罗旗帜,岳珠峰,等. 薄壁箱梁剪力滞实验与计算研究 [J]. 公路交通科技,2004,21(2):73-76. WU You-ming, LUO Qi-zhi, YUE Zhu-feng, et al. Experimental and Analytical Study of the Shear Lag in Thin Walled Box Girders[J]. Journal of Highway and Transportation Research and Development, 2004,21(2):73-76. |
| [10] | 钱寅泉,倪元增.箱梁剪力滞计算的翘曲函数法 [J]. 铁道学报,1990,12(2): 57-70. QIAN Yin-quan, NI Yuan-zeng. Warping Displacement Function for Calculation of Shear Lag Effect in Box Girder [J]. Journal of the China Railway Society, 1990,12(2):57-70. |
| [11] | 韦成龙,曾庆元,刘小燕. 薄壁箱梁剪力滞分析的多参数翘曲位移函数及其有限元法 [J].铁道学报, 2000,22(5):60-64. WEI Cheng-long, ZENG Qing-yuan, LIU Xiao-yan. Warping Displacement Function and Finite Element Method for Calculation of Shear Lag Effect in Box Girder [J]. Journal of the China Railway Society, 2000,22(5):60-64. |
| [12] | 李立峰,彭鲲,王文. 波形钢腹板组合箱梁剪力滞效应的理论与试验研究 [J]. 公路交通科技,2009,26(4): 78-83. LI Li-feng, PENG Kun, WANG Wen. Theoretical and Experimental Study on Shear Lag Effect of Composite Box Girder with Corrugated Steel Webs[J]. Journal of Highway and Transportation Research and Development, 2009,26(4): 78-83. |
| [13] | 郑尚敏,万水. 钢桁腹组合梁剪力滞效应的有限元分析 [J]. 公路交通科技,2013,30(11): 68-72. ZHENG Shang-min, WAN Shui. Finite Element Analysis on Shear Lag Effect in Composite Girder with Steel Truss Webs[J]. Journal of Highway and Transportation Research and Development, 2013,30(11): 68-72. |
| [14] | 雒敏,蔺鹏臻,孙理想. 单箱双室箱梁的剪力滞效应分析 [J]. 力学与实践,2013,35(6):70-74. LUO Min, LIN Peng-zhen, SUN Li-xiang. Analysis of Shear Lag Effect of Twin-cell Box Girders [J]. Mechanics in Engineering, 2013,35(6):70-74. |
| [15] | 李丽元. 波形钢腹板组合连续箱梁剪力滞效应的理论与试验研究 [D]. 兰州:兰州交通大学,2012. LI Li-yuan. Theoretical and Experimental Research on Shear Lag Effect in Continuous Box-girder with Corrugated Steel Webs [D]. Lanzhou:Lanzhou Jiaotong University, 2012. |
| [16] | 王静. 单箱多室波形钢腹板箱梁的受力特性分析 [D]. 西安:长安大学,2011. WANG Jing. Analysis on Mechanical Characteristics of Single-box Multi-cell Girder with Corrugated Steel Webs [D]. Xi'an: Chang'an University, 2011. |
 2015, Vol. 31
2015, Vol. 31
