扩展功能
文章信息
- 李苗, 任伟新, 黄天立, 王宁波
- LI Miao, REN Wei-xin, HUANG Tian-li, WANG Ning-bo
- 基于EMD与IMF能量的桥梁应变温度效应成分的提取
- Extraction of Bridge Strain Temperature Effect Based on EMD and IMF Energy
- 公路交通科技, 2015, Vol. 31 (7): 62-68
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (7): 62-68
- 10.3969/j.issn.1002-0268.2015.07.011
-
文章历史
- 收稿日期:2014-09-26
2. 中南大学 土木工程学院, 湖南 长沙 410075;
3. 合肥工业大学 土木与水利工程学院, 安徽 合肥 230009
2. School of Civil Engineering, Central South University, Changsha Hunan 410075, China;
3. School of Civil Engineering, Hefei University of Technology, Hefei Anhui 230009, China
大跨度桥梁结构长期监测的应变信号不可避免地受到运营环境因素的影响,在不同时间尺度下应变时程主要反映两类荷载信息:一类是温度荷载信息,另一类是以车辆为主的活载信息。较大的环境温度变化产生的温度应变可能会大于桥梁动荷载引起的应变[1, 2],使得反映结构动力特性的信号特征被幅值更大的温度应变信号所掩盖,从而影响对桥梁实际运营状况的有效判别。
桥梁结构应变时程主要由活荷载效应成分与温度荷载效应成分(周期趋势)构成,具有非平稳性。消除时程中的温度效应成分,可视作从时间序列里提取周期趋势项的问题。在早期对时间序列的研究中,将趋势看作时间序列长时间的动向。较常用的提取方法主要有最小二乘拟合法、ARMA时间序列模型和低通滤波法等[3]。但最小二乘拟合法适用于趋势项的类型为已知的信号,如线性趋势、多项式趋势或指数趋势等,难以处理具有复杂变化趋势或随机变化趋势的数据;ARMA模型是最常用的时间序列模型,它建立在线性动态结构的基础之上,本质上是线性模型,适合满足有限参数线性模型的平稳时间序列的分析。从频域出发,采用滤波的方法[4, 5, 6]可提取时间序列中不同的频率成分,其最基本的工具就是傅里叶变换和滤波器等。动应变信号中的温度效应成分相对活载效应成分具有慢变的特点,可考虑低通滤波获得温度应变。但低通滤波法必须恰当地选择滤波器参数和截止频率,否则会产生较大的误差。这些分离方法大都是以傅立叶变换为其最终理论依据的,傅立叶变换理论中的时域基本信号是平稳的简谐波信号。由N. E. Huang提出的经验模态分解法(EMD)[7],依据数据自身的时间尺度特征进行信号分解,该方法基于瞬时频率,是局部的和自适应的,适合于研究非平稳的信号[8]。
EMD提取应变信号中的温度效应成分实质上是提取信号中周期趋势成分的问题,可通过将多阶与周期趋势相关的IMF叠加得以实现。因此,IMF的选取是该方法的关键。笔者分别在时域和频域对信号各阶IMF的能量特征进行分析,基于能量突变阶数与Hilbert边际谱相关系数确定IMF阈值,然后通过阈值选取相关IMF重构周期趋势成分,以此提取应变中的温度效应。 1 EMD方法与趋势成分 1.1 EMD基本理论
经验模态分解将一个信号分离为数阶本征模态函数(IMF)Ii(t)与一个余量rn(t)之和[7]。本征模态函数视为信号中的振动成分,反映了信号中不同频率的成分。从原始信号中先分离出来的本征模函数较后分离出来的频率低,余项的频率最低,为趋势成分:

原始信号分解所得余项一般为单调函数,其周期大于实测信号的长度,即为信号的趋势项[9]。经验模态分解可在无任何先验假定条件下,通过分解得到余项来提取信号中的趋势项。然而,振动信号中的趋势成分通常具有明确的物理意义,如大跨度桥梁结构应变时程中的趋势成分对应于结构的温度应变。由温度应力形成的应变时程表现为与温度变化相似的波动形式,由余项代表的单调趋势与温度应变对应的周期趋势存在差异,即从应变时程提取出的余项不能等同于温度应变。因此,在提取振动信号中的趋势项之前有必要先明确信号中趋势的物理含义。 2 IMF能量与阈值选取
假定原始信号x(t)为宽带信号y(t)和周期趋势成分g(t)的叠加,从原始信号中较准确地提取周期趋势成分,应先确定周期趋势的IMF成分构成。信号中的周期趋势成分g(t)是个相对的慢变过程。因此,周期趋势的构成应是多组末阶IMF与余项的组合。采用经验模态分解法提取应变时程中的温度效应,归结于如何确定IMF的阶数阈值,
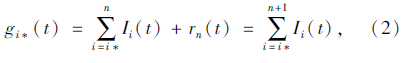
陈隽[10]等提出了基于EMD方法在不同频率限制要求下信号趋势项的定义和提取方法。周毅[11]等对动应变信号的各阶IMF进行自功率谱分析,应变响应的动、静成分分离以结构基频为阈值,由低于基频的分量相加得到静态应变响应。有学者从信号能量的角度对各阶IMF展开了研究[12, 13]。这也是本文的研究出发点,通过在时域与频域对信号各阶IMF的能量分析综合确定提取应变信号中温度效应的IMF阶数阈值。 2.1 时域分析
对任一信号 ,定义第i阶IMF的能量为 :

Rilling[13]、Moghtaderi[14]分析了分数高斯噪声和高斯白噪声的各阶IMF,发现IMF的能量随阶数的增大而变小。基于这一结论,本文在仿真实例中对由高斯白噪声与周期趋势成分叠加而成的信号进行分析,以了解周期趋势成分对信号IMF能量变化的影响。 2.2 频域分析
将信号分解为数组IMF,Ii(t)的瞬时幅值和瞬时频率可以通过Hilbert变换计算得到[7]。对Ii(t)作Hilbert变换,得到解析信号:








对于数字信号,Ii(t)的边际谱表示为:

文献[15]指出边际谱的物理意义,边际谱是Hilbert谱H(f,t) 对时间的积分。对任意固定频率f的时间积分就是时间t内频率f对应的幅值之和,边际谱从统计意义上表征了每个频率点的累积幅值分布。因此,边际谱反映了瞬时频率f(t)处的信号的总幅值(总能量)大小。也可认为,任一瞬时频率都有一定的能量,将所有时刻某一瞬时频率的能量(幅值)加起来就是信号中该频率的总能量(总幅值)。
假定原始信号由两组不同频率的信号成分构成,且所处的频带间隔较大,可以理解信号的包络主要取决于信号的低频成分;若两组信号成分所处的频带较紧密,则原始信号的包络与两组信号成分均相关。因此,从应变信号分解所得的一系列IMF中若存在多个末阶IMF的边际谱和余项的边际谱紧邻,可以认为:(1)这些IMF和余项在频域的能量分布模式近似;(2)应变信号的周期趋势成分应由多个末阶低频IMF与余项构成。若未完整选出构成周期趋势的低频IMF,将丢失原始信号中的部分周期趋势信息。
连续两阶IMF的边际谱在频域的相邻程度,通过相关系数来衡量:
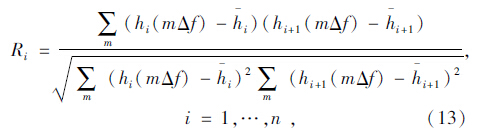
两组仿真信号x(t)都由高斯白噪声信号wn(t)与周期趋势成分g(t)叠加而成。信号一x1(t):高斯白噪声信噪比为10 dB,周期趋势成分g1(t)=at+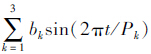 ,参数a=2×10-3,bk=0.6,从k=1到3,分别等于360,720,1 400 s,采样间隔Δt=1 s,共4 000个样本,见图 1(a)。信号二x2(t):高斯白噪声信噪比为17 dB,周期趋势成分g2(t)=-
,参数a=2×10-3,bk=0.6,从k=1到3,分别等于360,720,1 400 s,采样间隔Δt=1 s,共4 000个样本,见图 1(a)。信号二x2(t):高斯白噪声信噪比为17 dB,周期趋势成分g2(t)=- an(t/50)n+
an(t/50)n+ bkcos(2πt/Pk),参数a1=0.2,a2=0.01;b1,b2分别为20,50;P1,P2分别为300,700,采样间隔与样本数同信号x1(t),见图 1(b)。
bkcos(2πt/Pk),参数a1=0.2,a2=0.01;b1,b2分别为20,50;P1,P2分别为300,700,采样间隔与样本数同信号x1(t),见图 1(b)。

|
| 图 1 模拟得到的时域信号 Fig. 1Simulated time domain signal |
EMD分解两组信号,从第6阶开始,IMF逐步表现为周期较长的波动曲线形式。通过式(3)计算信号各阶IMF(包括余项)在时域的能量,两组信号的IMF能量(图 2)从第1阶至第5阶持续减小,在第6阶呈现明显的增大,与高斯白噪声各阶IMF能量递减的结果不同。根据IMF时域能量陡增的现象,可考虑选择阶数阈值为6。

|
| 图 2 信号各阶IMF的能量 Fig. 2Each order IMF energy of signal |
计算信号各阶IMF的边际谱,得到IMF在频域的能量分布。图 3所示为归一化后的IMF边际谱,观察两组信号的IMF1~IMF5边际谱曲线形式差异明显,且形式差异较大的谱曲线分离程度也较大(如图 3中的IMF1与IMF2)。因此,可通过计算两相邻IMF(IMFi与IMFi+1)边际谱曲线的相关系数Ri(边际谱曲线的相似度)来判断相邻谱曲线的分离程度。根据式(13)计算信号各IMF的边际谱相关系数,这里为避免边际谱幅值对计算结果的影响,对边际谱做归一化处理后再计算相关系数,见表 1。

|
| 图 3 各阶IMF归一化的边际谱 Fig. 3Normalized marginal spectrum of each order IMF |
| 信号 | R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 | R9 | R10 |
| x1(t) | -0.453 | 0.146 | 0.313 | 0.336 | -0.009 | 0.462 | 0.940 | 0.934 | 0.995 | 0.886 |
| x2(t) | -0.413 | 0.216 | 0.273 | 0.420 | -0.013 | 0.266 | 0.996 | 0.969 | 0.978 | 0.999 |
表 1显示,两组信号前7阶IMF边际谱的相关性较小,虽然IMF6与IMF7的能量Gi都较大,但R6值显示两者的谱曲线相关性不强,反映了IMF6与IMF7在频域的能量分布模式存在一定差异;相关系数R7~R10都大于0.88,说明IMF7~IMF11(余项)的谱曲线相邻较紧密,能量分布模式趋于一致,如图 3所示。根据在频域的能量分析结果,可考虑选择阶数阈值为7。
图 4(a)、图 5(a)中黑色虚线代表采用阈值7从信号一、二提取的波动曲线g′(t),与代表已知周期趋势的灰色曲线g(t)吻合度较好;采用阈值6提取的波动曲线g′(t) 如图 4(b)、5(b)所示,曲线局部具有一定毛刺,说明IMF6带入了相对短时的波动信息。综合能量Gi和边际谱的分析结果,确定IMF阈值为7。

|
| 图 4 信号x1(t)周期趋势提取结果 Fig. 4Extracted cycle trend from signal x1(t) |

|
| 图 5 信号x2(t)周期趋势提取结果 Fig. 5Extracted cycle trend from signal x2(t) |
所选i值作为阈值i∗是否恰当,通过周期趋势成分的相对误差来验证,见式(14)。采用不同i值(IMF阶数)提取的周期趋势成分与已知周期趋势成分g(t)的欧式距离为Ei,g(t)的欧式范数为E,结果见表 2。i取7时,周期趋势成分相对误差最小,说明宜取i=7为IMF阈值i*。

| 阈值i | 5 | 6 | 7 | 8 |
| x1(t) | 10.864 | 7.625 | 3.490 | 55.945 |
| x2(t) | 5.082 | 3.769 | 1.643 | 29.929 |
综合以上分析结果,确定IMF阈值可先根据IMF在时域的能量Gi突变阶数i,初步选取可能的IMF阈值(阶数)最小值i′min;在i≥i′min的范围内,再采用首个超过0.8(相关度高)的边际谱相关系数Ri对应的阶数i作为IMF阈值i*。 4 实测数据分析
所分析实测数据为大跨度悬索桥的钢桁梁应变,测点布置于梁跨中的上弦杆,采样频率1 Hz,测试时长为2 d(数据I、II)。测试期间以晴朗天气为主,昼夜温差较大,结构温度应力的变化使应变时程在24 h内呈现明显的长周期波动。 4.1 温度应变的提取
分析2 d应变时程各阶IMF的能量Gi变化情况,前6阶IMF能量新增后减,这种现象应该与应变时程的成分有关。应变时程主要是由结构温度应力等引起的周期趋势成分与交通荷载引起的脉冲形式成分叠加而成,而非高斯白噪声与周期趋势的叠加。从第7阶开始Gi逐渐增大,但增幅不明显,可初步选定IMF阈值在7~9范围内(图 6)。应变时程IMF7~IMF9的边际谱相关系数都小于0.65;第9阶后,IMF9~IMF16的相关系数稳定在0.8以上(表 3)。

|
| 图 6 应变信号各阶IMF的能量 Fig. 6Each order IMF energy of strain signal |
| 数据 | R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 |
| Ⅰ | 0.493 | 0.661 | 0.621 | 0.566 | 0.464 | 0.413 | 0.653 | 0.511 |
| Ⅱ | 0.498 | 0.673 | 0.620 | 0.525 | 0.499 | 0.425 | 0.529 | 0.436 |
| 数据 | R9 | R10 | R11 | R12 | R13 | R14 | R15 | |
| Ⅰ | 0.965 | 0.999 | 1 | 1 | 1 | 1 | 0.995 | |
| Ⅱ | 0.875 | 0.999 | 0.999 | 1 | 1 | 1 | 1 |
综合应变信号IMF的能量突变起始阶数和边际谱相关系数,选取IMF阈值为9。将IMF9~IMF16叠加所得即原始应变时程(图 7灰色线)中反映结构温度应力变化的温度效应成分(黑色曲线)。

|
| 图 7 原始应变时程与温度效应提取结果 Fig. 7Extracted raw strain time history and temperature effect |
对提取结果的检验可从原始应变的成分叠加这一特点出发,若原始应变中的温度应变被完整提取,余下的应变信息(活载效应成分)应与原始应变数据中的活载信息一致;否则,说明部分温度应变已混杂到活载效应成分当中。该检验方法即通过活载效应成分中动载信息的完整程度来反映温度应变是否得到有效、正确的提取。
图 7(a)原始应变时程采用阈值9提取温度效应成分后所得活载效应成分(IMF1~IMF8构成)如图 8所示。任取图 7(a)、图 8相同时段的应变曲线对比(图 9),两曲线吻合较好,说明车载产生的应变幅保存完整。

|
| 图 8 活荷载应变成分 Fig. 8Strain component induced by live load |

|
| 图 9 局部时段应变时程曲线对比 Fig. 9Comparison of partial strain time history curves |
为进一步检查从长时间数据分离出的活载效应成分是否较完整地保留了原始数据中的活载信息,可采用雨流计数法对原始应变时程和活载效应成分的应变幅和循环次数进行统计分析[16]。观察两天的应变时程,110 με左右的应变幅是测试期间最大车载情况下产生的,即最大应力幅约23 MPa。将该幅值范围内的应力循环次数列于表 4。从统计结果来看,活载效应成分与原始应变时程在各级应力幅下的循环次数差别较小,说明温度应变的提取对活载应变信息影响小,也说明原始应变中温度应变的提取较为完整。
| 测试 | 1 MPa | 3 MPa | 5 MPa | 7 MPa | 9 MPa | 11 MPa | 13 MPa | 15 MPa | 17 MPa | 19 MPa | 21 MPa | 23 MPa |
| Ⅰ/原始 | 891 | 722 | 403 | 321 | 269 | 163 | 88 | 39 | 21 | 10 | 7 | 7 |
| Ⅰ/活载效应 | 889 | 721 | 405 | 319 | 271 | 168 | 82 | 38 | 21 | 13 | 6 | 8 |
| Ⅱ/原始 | 909 | 771 | 469 | 414 | 269 | 152 | 81 | 34 | 17 | 10 | 2 | 0 |
| Ⅱ/活载效应 | 915 | 766 | 470 | 413 | 268 | 155 | 79 | 34 | 19 | 9 | 3 | 0 |
(1) 利用EMD提取应变信号中具有周期趋势特点的温度效应成分,关键在于确定重构周期趋势的IMF阈值。对仿真和实测数据的研究表明:信号中的周期趋势成分使得IMF能量存在阶数突变;构成周期趋势的末阶IMF边际谱曲线的相关性较强,相关系数超过0.8,说明在频域的能量分布模式较为一致。
(2) 综合应变信号IMF的能量突变阶数和边际谱相关系数确定了IMF阶数阈值,将高于阈值的末阶IMF叠加即得到应变信号中的温度效应成分。
(3) 通过雨流计数法对应变幅的统计,提取温度效应后的应变时程仍较完整地保留了车载信息,结果验证了该提取方法的有效性。
| [1] | CATBAS F N,SUSOY M,FRANGOPOL D M. Structural Health Monitoring and Reliability Estimation: Long Span Truss Bridge Application with Environmental Monitoring Data[J]. |
| [2] | HELMICKI A,HUNT V,SHELL M,et al. Multidimensional Performance Monitoring of a Recently Constructed Steel-stringer Bridge[C]// Proceedings of the 2nd International Workshop on Structural Health Monitoring. Palo Alto:Stanford University,1999:408-416. |
| [3] | BENDAT J S,PIERSOL A G. Random Data:Analysis and Measurement Procedures[M]. New York:John Wiley and Sons,1986:396-398. |
| [4] | POLLOCK D S G. Methodology for Trend Estimation[J]. |
| [5] | POLLOCK D S G. Filters for Short Non-stationary Sequences[J]. |
| [6] | CHRISTIANO L J, FITZGERALD T J. The Band Pass Filter[J]. |
| [7] | HUANG N E,SHEN Z,LONG S R,et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J]. |
| [8] | 叶贵如,徐欣. HHT变换在桥梁损伤诊断中的应用[J]. 公路交通科技,2009,26(9):97-101. YE Gui-ru,XU Xin. Appliance of Hilbert-Huang Transform in Bridge Health Monitoring[J]. Journal of Highway and Transportation Research and Development,2009,26(9):97-101. |
| [9] | WU Z,HUANG N E,LONG S R,et al. On the Trend,Detrending,and Variability of Nonlinear and Nonstationary Time Series[J]. |
| [10] | 陈隽,李杰. 振动信号趋势项提取的几种方法及其比较[J]. 福州大学学报:自然科学版,2005,33(增1):42-45. CHEN Jun,LI Jie. Methods for Signal Trend Extraction and their Comparison[J]. Journal of Fuzhou University:Natural Science Edition,2005,33(S1):42-45. |
| [11] | 周毅,孙利民,闵志华. 斜拉桥主梁应变监测数据分析[J]. 振动与冲击,2011,30(4):230-235. ZHOU Yi,SUN Li-min,MIN Zhi-hua. Girder Strain Analysis of a Cable-stayed Bridge[J]. Journal of Vibration and Shock,2011,30(4):230-235. |
| [12] | WU Z,HUANG N E. A Study of the Characteristics of White Noise Using the Empirical Mode Decomposition Method[J]. |
| [13] | RILLING G,FLANDRINl P,GONCALVES P. Empirical Mode Decomposition,Fractional Gaussian Noise and Hurst Exponent Estimation[C]// ICASSP 2005 IEEE International Conference on Acoustics,Speech and Signal Processing. Philadelphia:IEEE, 2005:489-492. |
| [14] | MOGHTADERI A, FLANDRIN P, BORGNAT P. Trend Filtering Via Empirical Mode Decompositions[J]. |
| [15] | 钟佑明,秦树人,汤宝平. 希尔伯特-黄变换中边际谱的研究[J]. 系统工程与电子技术,2004,26(9): 1323-1326. ZHONG You-ming,QIN Shu-ren,TANG Bao-ping. Study on the Marginal Spectrum in Hilbert-Huang Transform[J]. Systems Engineering and Electronics,2004,26(9): 1323-1326. |
| [16] | 刘建,桂勋,李传习. 基于健康监测的自锚式悬索桥钢箱梁细节疲劳可靠度研究[J]. 公路交通科技,2015,32(1):69-75. LIU Jian,GUI Xun,LI Chuan-xi. Study on Fatigue Reliability of Details of Steel Box Girders of a Self-anchored Suspension Bridge Based on Health Monitoring[J]. Journal of Highway and Transportation Research and Development,2015,32(1):69-75. |
 2015, Vol. 31
2015, Vol. 31
