扩展功能
文章信息
- 曹海莹, 刘云飞, 李慧剑, 吴吉贤
- CAO Hai-ying, LIU Yun-fei, LI Hui-jian, WU Ji-xian
- 上覆硬壳层软土路基土层界面动力响应特征及工程应用
- Dynamic Response Characteristic of Interface of Layer of Soft Soil Subgrade with Dry Crust Covering and Its Engineering Application
- 公路交通科技, 2015, Vol. 31 (7): 33-40
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (7): 33-40
- 10.3969/j.issn.1002-0268.2015.07.007
-
文章历史
- 收稿日期:2014-11-12
目前,随着交通工具行驶速度的提升,以及重载车辆的不断出现,导致路基在往复交通荷载作用下发生严重的变形累积和土体损伤,这对道路工程的正常运营造成了不可忽视的工程隐患[1]。研究交通荷载在土体中产生的动应力分布规律和传递模式是解决上述问题的关键[2],但是由于土体性质的复杂性、交通荷载的随机性等诸多因素的影响,有关路基土动力响应方面的研究工作尚处于不成熟阶段[3, 4]。
上覆硬壳层软土地基是路基工程中一种典型的土层分布形式[5],因为硬壳层本身强度高、抗变形能力强,如何揭示和挖掘其力学潜能,一直是备受国内外学者关注的热点[6, 7, 8]。而针对车辆荷载作用下上覆硬壳层软土路基动力响应方面的研究却鲜见报道。
研究交通荷载引起的地基土动力特性问题,目前比较常用的方法包括:理论解析法[9]、数值模拟方法[10]、室内模型试验[11]以及微观结构分析法[12]和现场实测法[13]等。每种方法均存在自身的优缺点,比如:理论解析方法的表达式相对比较复杂,求解难度大;数值模拟方法虽能避免繁琐的公式推导,土体参数选取、边界条件假定等因素对其计算精度的影响却较大;室内模型试验中需要解决材料相似性和尺寸效应等问题;构建土体微观结构变化与宏观力学特性的对应关系是微观结构分析法应用的关键;实测数据可真实反映土体动力特性的演化规律,但现场实施监测的案例并不多见。
综合上述分析,本文依据应力波理论和数值模拟结果,提出一种能够直观表征硬、软土层界面处动应力传递模式的计算方法,并与现场实测数据及其他方法进行比对,该方法可用于评估车辆荷载作用下路基土的力学状态,预测其残余变形值,为挖掘硬壳层在动力范畴的力学特性提供了新的研究思路。 1 动应力突变存在的理论基础 1.1 应力波理论的应用及假定
行车荷载产生的振动可以看成是以应力波的形式在地基土中传播[14],而有关应力波的理论已较为成熟[15],且在岩土工程中的应用也取得了一定成果[16],采用应力波理论开展相关研究工作具有可行性。为了计算方便,做出如下几点假定:
(1)车辆荷载引起的地基土动应变很小,土体一般属于弹性变形阶段[17]。因此,假定上覆硬壳层软土路基为多层弹性介质,即车辆荷载在地基土中产生的应力波属于弹性波。
(2)土层的界面效应对于土体饱和度十分敏感,当土体处于准饱和状态时,反射和透射系数数值较稳定[18],故假定上覆硬壳层软土路基土处于准饱和状态。
(3)车辆荷载在地基土中的影响深度在1.5~8.0 m左右[19],假定其影响深度大于上覆硬壳层厚度(一般在1.5~5.0 m),即动应力可传至下卧软土层中。
1.2 透射系数计算
因为上覆硬壳层与下卧软土层的波阻抗不匹配,当车辆荷载产生的入射应力波传至硬、软两土层界面处时,会产生反射应力波和透射应力波,如图 1所示。
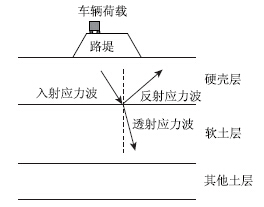
|
| 图 1 土层界面处应力波传递Fig. 1 Stress wave transmitting at soil interface |
透射系数的计算公式为:
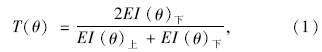
因为需要考虑应力波的叠加效应,弹性阻抗采Whitcombe提出的归一化表达式[20]:
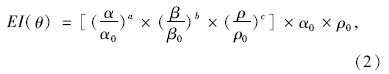
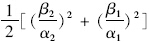 ;α0,β0,ρ0为参考常数;ρ为土层密度;θ为纵波入射角;α为纵波波速;β为横波波速。
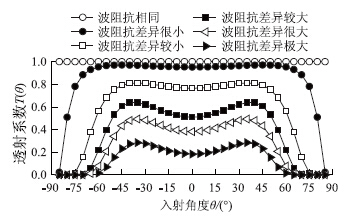
;α0,β0,ρ0为参考常数;ρ为土层密度;θ为纵波入射角;α为纵波波速;β为横波波速。依据公式(1)、(2),按照硬、软土层波阻抗的差异性大小,选取多组土体参数展开计算,其计算结果如图 2所示。
|
| 图 2 透射系数分布曲线Fig. 2 Distribution curves of transmission coefficient |
从图 2中可以看出,透射系数与入射角度θ和硬、软土层波阻抗的差异性密切相关,除波阻抗相同(均质地基)的情况外,在θ=[0,90)区间内,随着入射角度θ的增大,透射系数呈现先增大后降低的变化趋势。以θ=0°为例,随着硬、软土层波阻抗的差异性增大,透射系数在逐渐降低,这表明硬壳层性质越好(波阻抗越大),对弱化和扩散动应力越有利。从动应力衰减角度,透射系数可近似定义为入射应力波与透射应力波的动应力峰值之比。由于T(θ)<1.0,在硬、软土层界面处动应力峰值将发生突变现象(数值降低),从能量守恒角度解释,入射波能量=透射波能量+反射波能量,应力波由硬壳层透射至软土层,其能量必然发生衰减。
透射系数虽能近似表征土层界面处动应力的衰减规律,但是这种方法仍存在以下不足:
(1)仅考虑了硬、软土层的密度和波速,未考虑硬壳层厚度这一重要因素;
(2)硬壳层表面作用的初始动应力水平大小也是影响因素之一,该方法中并未体现;
(3)公式复杂、计算量大,不宜在实际工程中应用推广;
(4)透射系数随入射角度θ波动较大,取值不稳定。 2 动应力传递规律的数值模拟
借助数值模拟软件FLAC3D的动力分析功能,构建和编写计算模型与求解程序,对车辆荷载作用下上覆硬壳层软土路基的动应力传递规律展开研究。 2.1 车辆荷载表达式
车辆荷载采用常用表达式:
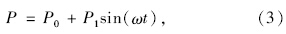
车辆荷载被施加在路堤表面,即考虑路堤对动能量的消耗作用。由于几何模型具有对称性,采用1/2模型进行分析,同时考虑车辆荷载的影响范围,最终选取模型尺寸为25 m×50 m×10 m(宽×长×高),网格尺寸取0.2 m。模型底部采用静态边界条件,4个侧面的边界采用自由场,以降低边界条件对动荷载传播的影响。计算模型如图 3所示,图中示意的荷载位置,代表重型卡车4个车轮与路面的接触面积大小。

|
| 图 3 数值计算模型Fig. 3 Numerical calculation model |
土体本构模型采用Mohr-Coulomb模型(FLAC3D动力分析中允许采用静力本构模型,关键是设置好阻尼形式和边界条件)。土体计算参数以表 1为例进行分析,路堤填高取2.0 m,填土容重为19.6 kN/m3,路堤顶宽28 m,边坡坡度1∶1.5。
| 土层 | 厚度/m | 密度/(kg·m-3) | 黏聚力/kPa | 内摩擦角/(°) | 体积模 量/MPa | 切变模 量/MPa | 泊松比 |
| 硬壳层 | 1.5 | 1 865 | 22 | 25 | 12.3 | 12.3 | 0.27 |
| 软土层 | 6.5 | 1 630 | 5 | 11 | 3.2 | 3.2 | 0.33 |
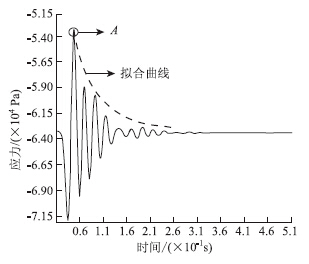
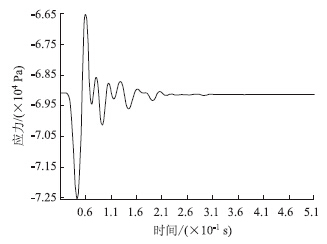
在图 3中坐标原点(x=y=0)定在荷载作用区域的中心,图 4、图 5所示竖向动应力时程曲线对应测点的坐标为(x=y=0,z),其纵坐标代表总应力,在计算竖向动应力时应扣除自重应力部分。
|
| 图 4 硬壳层中应力时程曲线(z=1.40 m)Fig. 4 Stress-time curves in dry crust(z=1.40 m) |
|
| 图 5 卧软土层中应力时程曲线(z=1.60 m)Fig. 5 Stress-time curves in subjacent soft soil layer(z=1.60 m) |
在t=0.05 s时刻,竖向动应力从埋深1.40 m(硬壳层底部)传至1.60 m(软土层顶部)处,其峰值由10 kPa衰减至3 kPa,进一步验证了硬、软土层界面处存在的动应力突变现象。从竖向动应力时程曲线的特征看,属于正常阻尼振动情况,将同一条竖向动应力时程曲线中各应力幅值点连线,其衰减规律可以用负指数函数曲线进行拟合[21],见图 4中的拟合曲线。
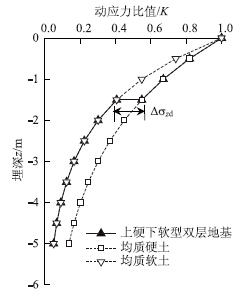
沿深度方向将各动应力时程曲线峰值点A的坐标进行连线,如图 6所示,其衰减规律同样符合负指数函数特征,横坐标表示z深度处竖向动应力峰值与地表处竖向动应力之比K。显然,竖向动应力在均质软土中的衰减速度要快于均质硬土,而在上硬下软型双层地基中,竖向动应力先是按均质硬土衰减路径变化,在土层界面处发生突变(动应力突变量定义为Δσzd),转而按均质软土衰减路径变化,且衰减深度滞留在下卧软土层内。
|
| 图 6 竖向动应力衰减曲线Fig. 6 Attenuation curves of vertical dynamic stress |
值得注意的是,改变式(1)中的车辆荷载以及表 1中的土体参数大小,重新输入命令流展开数值计算,所获得的上硬下软型双层地基竖向动应力衰减曲线仍大致符合上述变化规律。 3 动应力土层界面传递系数 3.1 公式推导
依据数值模拟结果,并参照文献[22, 23]有关结论,竖向动应力衰减曲线的数学表达式可写为:
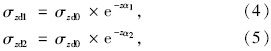
在硬、软土层的上界面和下界面分别代入各自土体的能量吸收系数,便会在土层界面上产生动应力突变增量Δσzd(如图 6所示)。
联合式(4)、(5)推导可知:
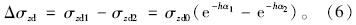
为了简化计算过程,引入变量η,η为软、硬土层界面处竖向动应力峰值的比值(以下简称动应力界面传递系数),用以表征土层界面上动应力突变增量的演化规律,即:

分别对式(4)、(5)两边取对数,并对两式进行减法运算,利用对数运算法则,可得:
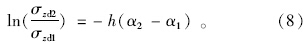
再将式(7)代入到式(8)中,得出:

可见,在式(9)中已经消除了σzd0的影响。依据应力波理论,硬壳层厚度和土体能量吸收系数可认为是应力波的几何阻尼和材料阻尼影响参数。参考《动力机器基础设计规范》(GB50040—96)对土体能量吸收系数α1,α2的数值范围,依据(α2-α1)的大小将硬、软土层性质的差异性划分为5个区域等级。
区域等级I:α2-α1∈(0,0.05),表示硬、软土层性质差异很小;区域等级II:α2-α1∈[0.05,0.1),硬、软土层性质差异较小;区域等级III:α2-α1∈[0.1,0.15),硬、软土层性质差异较大;区域等级IV:α2-α1∈[0.15,0.2),硬、软土层性质差异很大;区域等级V:α2-α1>0.2,硬、软土层性质差异极大。
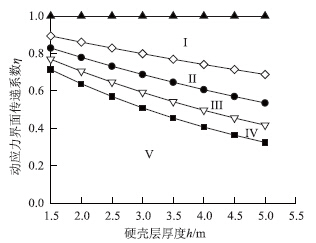
利用式(9)计算的结果如图 7所示。
|
| 图 7 界面传递系数分布曲线Fig. 7 Distribution curves of interface transfer coefficient |
已知硬壳层的厚度及硬、软土层性质的差异性,仅需在图 7中采用线性内插的方法就能获取到动应力界面传递系数η(以下简称本文方法),η值的变化范围一般在III、IV两个区域等级。 3.2 数据验证与分析
邢台—临西高速公路(以下简称邢临高速)经勘察,查明穿越区软土地基表层存在厚度为1.5~3.0 m的硬壳层(属厚硬壳层地质条件),属典型的上覆硬壳层软土路基,主要分布于K33+550~K39+990区间和K51+550~K60+455区间,路堤填高为2 m左右(属低路堤情况)。分别在K33+650、K38+650、K39+990和K51+650共4个监控断面沿埋深方向各埋设了5个XHZ-4XX型电阻应变式动态土压力盒,主要分布于硬壳层和下卧软土层内,用以监测交通运营期路基中竖向动应力的变化规律,4个监控断面的土体物理力学参数见文献[5]。因为监测时间不同,监测断面上经过的车辆类型和车速差别较大,导致监测数据量很大,整理出若干组代表性数据作为参考(重型卡车经过情况,车速为80~100 km/h,此时土体内动应力峰值较为明显),受篇幅所限,仅给出4组数据(其他数据验证的结果与之近似),如图 8所示。

|
| 图 8 实测动应力曲线Fig. 8 Curves of measured dynamic stress |
在图 8中,硬、软土层的动应力峰值之比可计算得出土层界面动应力传递系数,称为实测法。将透射系数法、本文方法和文献法与实测法进行比对,结果见表 2。三者与实测值之间的误差范围分别为6.83%~25.78%,10.24%~18.69%以及39.47%~68.35%。其中,透射系数法按照入射角度θ=0°的情况计算,其误差变化范围较大(入射角度θ取其他值的情况,其计算结果更不稳定);本文方法误差变化范围较小,计算值趋于稳定,且控制在20%以内;文献法受其理论假定的约束,在土层界面处须满足应力连续性的条件,导致计算值均为1.0,并未反映出硬、软土层界面处应力突变现象。综上所述,本文方法在估算动应力传递系数方面具有可行性,依据所分析工程的局限性,其适用范围定义为如下特征:重载车辆作用、低路堤、厚硬壳层。
车辆荷载作用下的路基土动应力影响深度并不大,对于重载车辆作用下低路堤高速公路情况,动应力可传至下卧软土层中(影响深度一般仅限于下卧软土层内)。由于硬壳层抗变形能力强,且内部动应力峰值远未达到土体强度值,硬壳层所处的动力性状可基本认为是弹性状态,其变形值较小,因此,路基土的残余变形主要取决于下卧软土层。准确计算传至软土层的动应力大小,对于判断土体的动力性状、评价运营期路基土所处的危险状态等级和预估残余变形尤为重要。
根据文献[17],路基土的动力性状按照动应变εd大小可划分为3种:(1) εd<10-4时,处于弹性性状;(2) 10-4<εd<10-2时,处于弹塑性性状;(3) εd>10-2时,处于塑性性状。
首先,由式(10)对软土的动应变εd大小进行估算,进而判断土体的力学状态。

若土体处于弹性状态,利用式(11)对路基土残余变形值进行预估:
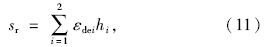
若土体处于弹塑性状态或塑性状态,路基土产生的残余变形值采用式(12)和(13)进行预估:
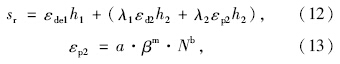
式(13)的符号含义和计算步骤参见文献[24]。 5 工程应用
邢临高速于2005年12月全线通车,依据路面变形的大小、行驶舒适度和路堤裂纹开展情况,并结合典型断面的实测沉降数据,于2013年7月—8月对重载交通作用较为频繁的上覆厚硬壳层软土路基段(路堤填高2 m左右)展开现场调查,结果表明,5%的区段运营效果较差或一般;15%的区段运营效果较好;80%的区段运营效果优良。
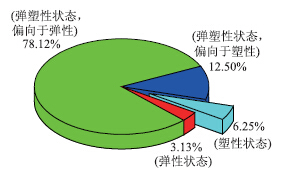
按照硬软土层的厚度比、硬软土层性质的差异性以及路堤填高等几个指标将上覆硬壳层软土路基段细划为32个区域,依据式(10)~ (13)的计算结果,上述区域下卧软土层的动力性状分布如图 9所示,其中处于弹性或趋于弹性状态的区域占到81.25%,路基残余变形预估值在0.3~2.6 cm之间;趋于塑性状态的区域占到12.50%,路基残余变形预估值在2.6~5.8 cm之间;处于完全塑性的区域占到6.25%,路基残余变形预估值在5.8~8.1 cm之间(邢临高速对软土段的工后沉降限制为10 cm)。
|
|
图 9 土体力学状态概率分布(考虑动应力突变)Fig. 9 Probability distribution of soil mechanical state (considering dynamic stress mutation) |
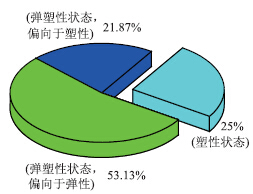
如果不考虑硬软土层界面处动应力突变特征,计算结果如图 10所示。其中趋于弹性状态的区域占到53.13%,路基残余变形预估值在1.8~3.7 cm之间;趋于塑性状态的区域占到21.87%,路基残余变形预估值在3.7~7.6 cm之间;处于完全塑性的区域占到25%,路基残余变形预估值在7.6~11.5 cm之间(超过工后沉降限制)。
|
| 图 10 土体力学状态概率分布(未考虑动应力突变)Fig. 10 Probability distribution of soil mechanical state (unconsidering dynamic stress mutation) |
显然,考虑硬、软土层界面处动力响应特征的预判结果与现场调查情况相比更为接近;与未考虑之的情况相比,明显降低了路基土处于完全塑性状态的比例(由25%降至6.25%),即路基残余变形值超出限值的概率被降低,这对客观评价工程质量和风险至关重要。如果在设计或施工阶段,对运营期内潜在不良区段展开科学评估,并预先采取相应工程措施,必将提高道路的整体通车运行质量。 6 结论
(1)从静力学角度,硬壳层的应力扩散效应是其壳体效应的具体表现形式;而在动力学范畴,借助理论推导、数值模拟和实测验证等多种手段,所揭示的在硬、软土层界面上存在动应力突变现象,是对硬壳层壳体效应内涵的一种补充。
(2)硬、软土层界面处动力响应特征的存在,对降低路基土的残余变形值十分有利,如何发挥和利用好这一性质对提高高速公路的通车运营效果具有重要意义。
(3)硬、软土层的性质差异性可以从不同角度展开评判,比如:土体的能量吸收系数、波阻抗以及压缩模量或刚度等,这些指标之间如何实现转换是未来研究的重点方向。
| [1] | 卢正, 姚海林, 骆行文, 等. 公路交通荷载作用下分层地基的三维动响应分析[J]. 岩土力学, 2009, 30(10): 2965-2970. LU Zheng, YAO Hai-lin, LUO Xing-wen, et al. 3D Dynamic Responses of Layered Ground under Vehicle Loads[J]. Rock and Soil Mechanics, 2009, 30(10): 2965-2970. |
| [2] | 汤连生, 林沛元, 吴 科, 等. 交通荷载下路基土中动应力响应特征分析[J]. 岩土工程学报, 2011, 33(11):1745-1749. TANG Lian-sheng, LIN Pei-yuan, WU Ke, et al. Response Characteristics of Dynamic Stress of Subgrade Soil under Vehicle Loads[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(11):1745-1749. |
| [3] | 刘汉龙. 土动力学与土工抗震研究进展综述[J].土木工程学报, 2012, 45(4):148-164. LIU Han-long. A Review of Recent Advances in Soil Dynamics and Geotechnical Earthquake Engineering[J]. China Civil Engineering Journal, 2012, 45(4):148-164. |
| [4] | AUERSCH L. The Effect of Critically Moving Loads on the Vibrations of Soft Soils and Isolated Railway Tracks[J]. Journal of Sound and Vibration, 2008, 3l(3):587-607. |
| [5] | 曹海莹, 窦远明. 上硬下软型双层路基应力扩散特征及工程应用[J]. 公路交通科技, 2012, 29(2):29-34. CAO Hai-ying, DOU Yuan-ming. Characteristics of Dry Crust's Stress Dispersion in Two-layer Roadbed and Its Engineering Application[J]. Journal of Highway and Transportation Research and Development, 2012, 29(2):29-34. |
| [6] | 张其一, 王青华, 王 琦. 上硬下软双层地基上条形基础穿刺深度研究[J]. 铁道工程学报, 2011(11):36-39. ZHANG Qi-yi, WANG Qing-hua, WANG Qi. Study on Punch through Depth of Two-layered Soil Foundation under Strip Footing[J]. Journal of Railway Engineering Society, 2011(11):36-39. |
| [7] | 郑健龙, 周驰晴, 张军辉. 双层地基一维固结特性研究综述[J]. 长沙理工大学学报:自然科学版, 2012, 9(1):1-10. ZHENG Jian-long, ZHOU Chi-qing, ZHANG Jun-hui. Summary of 1-D Consolidation Characteristics of Double-layered Ground[J]. Journal of Changsha University of Science and Technology: Natural Science Edition, 2012, 9(1):1-10. |
| [8] | KAZIMIEROWICZ-FRANKOWSKA K. Influence of Geosynthetic Reinforcement on the Load-settlement Characteristics of Two-layer Subgrade[J]. |
| [9] | 颜可珍, 吴罗成, 朱向平. 移动荷载作用下弹性半空间土体的动力响应[J]. 建筑科学与工程学报, 2011, 28(4):30-34. YAN Ke-zhen, WU Luo-cheng, ZHU Xiang-ping. Dynamic Response of Elastic Half-space Soil under Moving Loads[J]. Journal of Architecture and Civil Engineering, 2011, 28(4):30-34. |
| [10] | 仇敏玉, 俞亚南. 车辆荷载下地基数值模型的边界影响分析[J]. 公路交通科技, 2010, 27(1):39-42. QIU Min-yu, YU Ya-nan. Effect of Artificial Boundary on Numerical Model of Foundation under Vehicle Loads[J]. Journal of Highway and Transportation Research and Development, 2010, 27(1):39-42. |
| [11] | 常利武, 徐艳杰, 乐金朝. 动荷载作用下高温冻土路基动力响应的模拟试验研究[J]. 铁道学报, 2011, 33(11):80-84. CHANG Li-wu, XU Yan-jie, YUE Jin-chao. Simulation Experiment of Dynamic Responses of High Temperature Frozen Subgrade to Dynamic Loading[J]. Journal of the China Railway Society, 2011, 33(11):80-84. |
| [12] | 姜 岩, 雷华阳, 郑 刚, 等. 动荷载作用下结构性软土微结构变化的分形研究[J]. 岩土力学, 2010, 31(10):3075-3080. JIANG Yan, LEI Hua-yang, ZHENG Gang, et al. Fractal Study of Microstructure Variation of Structured Clays under Dynamic Loading[J]. Rock and Soil Mechanics, 2010, 31(10):3075-3080. |
| [13] | 赵俊明, 刘松玉, 石名磊, 等. 交通荷载作用下低路堤动力特性试验研究[J]. 东南大学学报:自然科学版, 2007, 37(5):921-925. ZHAO Jun-ming, LIU Song-yu, SHI Ming-lei, et al. Experimental Study on Dynamic Response of Low Embankment under Traffic Load[J]. Journal of Sourheast University:Natural Science Edition, 2007, 37(5):921-925. |
| [14] | 陈功奇, 高广运. 层状地基中填充沟对不平顺列车动荷载的隔振效果研究[J]. 岩石力学与工程学报, 2014, 33(1):144-153. CHEN Gong-qi, GAO Guang-yun. Vibration Screening Effect of In-filled Trenches on Train Dynamic Loads of Geometric Irregular Track in Layered Grounds[J].Chinese Journal of Rock Mechanics and Engineering, 2014, 33(1):144-153. |
| [15] | 吴世明. 土动力学[M]. 北京: 中国建筑工业出版社, 2000. WU Shi-ming. Soil Dynamics[M].Bejing: China Building Industry Press,2000. |
| [16] | 孙笑, 赵明阶, 汪魁, 等. 波动理论在岩土工程测试中的应用研究进展[J]. 重庆交通大学学报: 自然科学版, 2013, 32(1):58-62. SUN Xiao,ZHAO Ming-jie,WANG Kui, et al. Research on Application of Wave Theory in Geotechnical Engineering [J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2013, 32(1):58-62. |
| [17] | 曹艳梅, 夏禾. 基于Betti-Rayleigh动力互易定理求解移动荷载引起的地基土振动[J]. 岩石力学与工程学报, 2009, 28(7):1467-1476. CAO Yan-mei,XIA He. Solution of Foundation Soil Vibrations Induced by Moving Loads Based on Betti-rayleigh Dynamic Reciprocal Theorem[J].Chinese Journal of Rock Mechanics and Engineering, 2009, 28(7):1467-1476. |
| [18] | 徐平, 夏唐代. 弹性波在准饱和土和弹性土界面的反射与透射[J]. 力学与实践, 2006, 28(6):58-63. XU Ping, XIA Tang-dai. Reflection and Transmission of Elastic Wave at the Interface of Nearly Saturated Soil and Elastic Soil[J]. Mechanics in Engineering, 2006, 28(6):58-63. |
| [19] | 仇敏玉, 俞亚南. 道路行车荷载影响深度分析[J]. 岩土力学, 2010, 31(6):1822-1826. QIU Min-yu, YU Ya-nan. Analysis of Influence Depth for Roads Induced by Vehicle Load[J]. Rock and Soil Mechanics, 2010, 31(6):1822-1826. |
| [20] | WHITCOMBE D N.Elastic Impedance Normalization[J]. |
| [21] | 王杰贤. 动力地基与基础[M]. 北京: 科学出版社, 2001. WANG Jie-xian. Dynamic Ground and Foundation[M]. Beijing: Science Press, 2001. |
| [22] | 余艳华. 机械冲击荷载对邻近埋地管道的影响及控制研究[D]. 北京: 中国工程物理研究院, 2012. YU Yan-hua. Study on Influence and Control of Mechanical Impact Loads on Near Buried Pipeline[D].Beijing: China Academy of Engineering Physics, 2012. |
| [23] | 王礼立, 任辉启, 虞吉林, 等. 非线性应力波传播理论的发展及应用[J]. 固体力学学报, 2013, 34(3):217-240. WANG Li-li, REN Hui-qi, YU Ji-lin, et al. Development and Application of the Theory of Nonlinear Stress Wave Propagation[J]. Chinese Journal of Solid Mechanics, 2013, 34(3):217-240. |
| [24] | 李进军, 黄茂松, 王育德. 交通荷载作用下软土地基累积塑性变形分析[J]. 中国公路学报, 2006, 19(1):1-5. LI Jin-jun, HUANG Mao-song, WANG Yu-de. Analysis of Cumulative Plastic Deformation of Soft Clay Foundation under Traffic Loading[J]. China Journal of Highway and Transport, 2006, 19(1):1-5. |
 2015, Vol. 31
2015, Vol. 31
