扩展功能
文章信息
- 石振武, 解飞
- SHI Zhen-wu, XIE Fei
- 基于响应面分析法的钢纤维混凝土耐磨性试验研究
- Experimental Research of Abrasion Resistance of Steel Fiber Reinforced Concrete Based on Response Surface Analysis Method
- 公路交通科技, 2015, Vol. 31 (7): 23-27
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (7): 23-27
- 10.3969/j.issn.1002-0268.2015.07.005
-
文章历史
- 收稿日期:2014-06-09
近年来汽车超载超运现象随着我国经济的腾飞而频发,水泥混凝土路面在高强车载的频繁作用下,面层出现不同程度的磨损破坏,产生脱皮、麻面、露骨等劣化现象,而路面耐磨性能是影响道路行车舒适性和使用寿命的重要因素。研究表明钢纤维混凝土与素混凝土相比,由于乱向掺入的钢纤维增强了混凝土的整体性,使其克服素混凝土弯拉强度低、极限延伸率小、脆性等缺点,具有优良的抗拉、抗折强度和抗弯曲韧性[1, 2, 3, 4, 5],但是关于其耐磨性能却少有报道,因此探究钢纤维水泥混凝土路面的耐磨性具有现实意义。 1 试验设计原理
响应面分析法(Response Surface Methodology)多用于生物、化工试验设计,其原理是将多元二次回归方法作为函数估计工具,使多变量试验中因素与指标的相互关系用回归方程近拟,依此可对函数的响应面和等值线进行分析,研究变量与响应面、变量与变量的相互关系。该方法因具有试验次数少、成本低、精度高等优点,在试验和生产中成为解决多变量多因素问题的一种有效试验设计和分析方法[6]。
涉及水泥混凝土的材料试验,水胶比是表征其性能的最基本要素;而在确定钢纤维类型后,长径比和掺入混凝土体积率则是表征钢纤维性能的两个基本因素。因此本文通过响应面法设计钢纤维混凝土耐磨试验,以磨损量为响应值,波纹型钢纤维长径比、体积掺入率和钢纤维混凝土的水胶比为变量,研究3种因素对钢纤维混凝土耐磨性的影响次序以及建立耐磨模型分析优化,为钢纤维混凝土路面耐磨性研究提供参考。 2 试验设计 2.1 试验原材料
(1)钢纤维:采用嘉兴市七星钢纤维厂ZH-04波纹型扁平剪切纤维,如图 1所示;钢纤维具体指标见表 1。

|
| 图 1 波纹型扁平剪切钢纤维 Fig. 1Corrugated flat cut steel fiber |
| 长度/mm | 直径/mm | 抗拉强度/MPa | 重度/(kg·m-3) | 长径比 |
| 60.0 | 0.6 | 600 | 7 855 | 100 |
注:为达到响应面分析法试验设计对钢纤维长径比的不同要求,将钢纤维按照长径比要求切断使用 | ||||
(2)水泥:采用亚泰集团天鹅牌42.5级普通硅酸盐水泥,技术指标见表 2;
(3)骨料:粗骨料采用5~26.5 mm连续级配的石灰岩碎石,细集料采用细度模数2.83的天然河砂;
(4)外加剂:采用FDN-1型木质素磺酸盐类减水剂与XH-1型松香树脂类引气剂;
(5)水:哈尔滨市自来水。
| 细度/% | 比表面积/(kg·m-2) | 稠度/% | 凝结时间/min | 安定性 | 28 d强度/MPa | ||
| 初凝 | 终凝 | 抗折 | 抗压 | ||||
| 1.0 | 370 | 27.4 | 171 | 238 | 合格 | 8.4 | 53.4 |
钢纤维混凝土配合比设计由于各组成材料间交叉影响,较普通混凝土更为复杂[7]。目前业内已经明确的配合比概念为:砂率显著增大[8];需要较大的单位水泥用量[9]。因此试验结合响应面法设计分析,在保证钢纤维水泥混凝土力学性能和基本工作性能的基础上,提出如下的配合比设计,如表 3所示。
| 钢纤维长径比/mm | 掺入率/% | 水胶比 | 水/(kg·m-3) | 水泥/(kg·m-3) | 砂率/% | 集料/(kg·m-3) | 外加剂/(kg·m-3) |
| 20~100 | 0.5~2.0 | 0.35~0.4 | 165~188 | 470 | 48 | 1 745 | 4.6 |
《公路工程水泥及水泥混凝土试验规程》(JTG E30—2005)中规定水泥混凝土磨耗方法为水泥胶砂磨耗机对水泥混凝土试件进行60 r的磨轮磨耗,用磨损量评定水泥混凝土耐磨性[10]。但此方法是将水泥砂浆和粗集料一同磨损,无法准确模拟实际混凝土路面磨损过程中的磨粒磨损和疲劳磨损情况[11]。所以本试验方法参考陈瑜的水泥混凝土耐磨试验[12]。
混凝土为150 mm×150 mm×150 mm标准立方体试件,标养28 d。试验仪器: 磨石机、金刚砂、重物。试验方法:混凝土试件的上表面压重物模拟路面受车辆压力时的磨损状态。下表面放置在磨石机磨盘上。固定好试件,开动机器后,水流将金刚砂从入料口均匀地冲入高速旋转的磨盘上,金刚砂不断对试件的下表面冲击磨损。每块试件试验10 min,3块为一组,试验数据的处理方法参照混凝土耐磨试验。试件的耐磨性用磨损量表征。磨损量越小,表示试件耐磨性越好,反之耐磨性差。 3 钢纤维混凝土耐磨性响应面分析试验
响应面分析法设计本试验的中心思想是根据Box-Behnken Design(BBD)设计方法,选取钢纤维长径比、体积掺入率和水胶比作为响应因子,磨损量为响应值,利用Design Expert 7.0软件设计钢纤维水泥混凝土耐磨性试验,将试验结果进行回归近拟,分析出主效应和交互相应,求取最佳组合值。
具体试验设计方法是以钢纤维长径比A、钢纤维掺入率B和水胶比C,3个响应因子进行响应面分析设计,3种自变量±Level根据2.2节取值。编号1~12是析因试验,13~17是中心试验。其中前12组试验点为析因点,是自变量取值在A,B,C所构成的三维顶点;13~17组试验点为零点,是设计区域的中心点,零点试验重复5次估计试验误差。最后3组试验是根据响应面设计方法设计出的3组水胶比相对应的无钢纤维掺入的基准试验,如表 4所示。
| 编号 | 长径比A | 掺入率B/% | 水胶比C | 磨损量Y/g |
| 1 | 20.00 | 0.50 | 0.38 | 105.0 |
| 2 | 100.00 | 0.50 | 0.38 | 113.3 |
| 3 | 20.00 | 2.00 | 0.38 | 102.7 |
| 4 | 100.00 | 2.00 | 0.38 | 107.6 |
| 5 | 20.00 | 1.25 | 0.35 | 104.2 |
| 6 | 100.00 | 1.25 | 0.35 | 102.9 |
| 7 | 20.00 | 1.25 | 0.40 | 103.4 |
| 8 | 100.00 | 1.25 | 0.40 | 123.0 |
| 9 | 60.00 | 0.50 | 0.35 | 108..9 |
| 10 | 60.00 | 2.00 | 0.35 | 93.3 |
| 11 | 60.00 | 0.50 | 0.40 | 101.8 |
| 12 | 60.00 | 2.00 | 0.40 | 103.4 |
| 13 | 60.00 | 1.25 | 0.38 | 76.2 |
| 14 | 60.00 | 1.25 | 0.38 | 77.1 |
| 15 | 60.00 | 1.25 | 0.38 | 73.2 |
| 16 | 60.00 | 1.25 | 0.38 | 75.0 |
| 17 | 60.00 | 1.25 | 0.38 | 76.7 |
| 18 | — | — | 0.35 | 119.2 |
| 19 | — | — | 0.38 | 124.9 |
| 20 | — | — | 0.40 | 131.1 |
通过Design Expert 7.0的ANOVA方差分析功能对表 4中的3个因素A,B,C和相应值Y进行多元回归分析,得到回归方程与方差分析见表 5。
| 来源 | 平方和 | 自由度 | 均方差 | F | P>F |
| 模型 | 3 737.64 | 9 | 415.29 | 57.12 | <0.000 1 |
| A | 124.03 | 1 | 124.03 | 17.06 | 0.004 4 |
| B | 65.50 | 1 | 65.50 | 8.32 | 0.023 5 |
| C | 62.16 | 1 | 62.16 | 8.55 | 0.022 2 |
| AB | 2.89 | 1 | 2.89 | 0.40 | 0.548 4 |
| AC | 109.20 | 1 | 109.20 | 15.02 | 0.006 1 |
| BC | 73.96 | 1 | 73.96 | 10.17 | 0.015 3 |
| A2 | 1 522.80 | 1 | 1 522.80 | 209.45 | <0.000 1 |
| B2 | 657.11 | 1 | 657.11 | 90.38 | <0.000 1 |
| C2 | 792.29 | 1 | 792.29 | 108.97 | <0.000 1 |
| 残差 | 50.89 | 7 | 7.27 | ||
| 失拟项 | 40.96 | 3 | 13.65 | 5.50 | 0.066 6 |
| 绝对误差 | 9.93 | 4 | 2.48 | ||
| 总离差 | 3 788.53 | 16 | |||
注:(1) P>F小于0.05即可认为该指标显著;小于0.01时为高度显著;(2)R-Squared=0.986 6,Adj R-Squared=0.969 3,C.V.%=2.78 | |||||
回归方程:
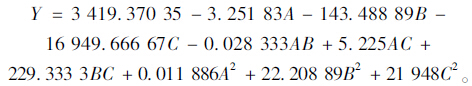
由表 5可知:F回归=57.12,大于F值的概率P<0.000 1,表明此模型极为显著;失拟项用来表示所用模型与试验的拟合程度,即二者差异的程度。本模型中P=0.066 6>0.05,表明此模型失拟项差异不显著,即试验数据与模型不相关的情况不显著,模型可信;模型复相关系数R-Squared=0.986 6,说明此模型与实际试验近似度的差异性为0.013 4,拟合较好;模型校正决定系数Adj R-Squared=0.969 3,可认为该模型的回归方程可模拟与解释96.93%的相应值变化,仅有总变异的3.07%不能用该模型解释;磨损量Y的变异系数C.V.表示试验的精确度,差异系数越小则试验的可靠性越高。本试验C.V.=2.78%,说明试验结果可信,所以可以用模型的回归方程代替试验真实点对试验结果进行分析。
因素A,B,C的P值均小于0.05,说明3种因素对磨损量的影响是显著的。P(A)<P(C)<P(B),说明在影响钢纤维混凝土耐磨性的因素中,钢纤维的长径比是最敏感的,其次是水胶比和掺入率。
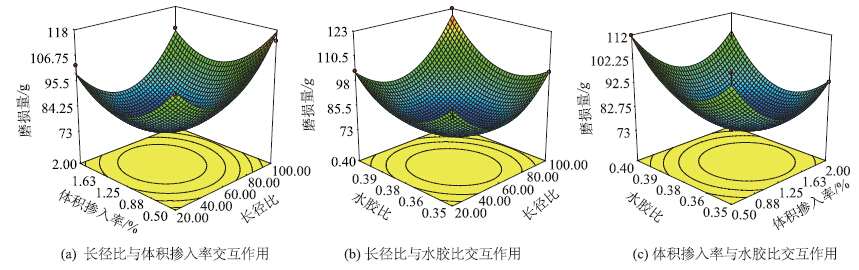
响应面分析三维图是响应值Y对应响应因子A,B,C所构成的空间曲面图。如图 2所示,从三维分析图可以直观看出各自变量对响应值的影响。
|
| 图 2 钢纤维长径比、体积掺入率、水胶比之间相互作用对磨损量影响三维相应曲面图 Fig. 2Three-dimensional curved surface of impact of interaction among length-diameter ratio,volume adding rate of steel fiber and water cement ratio on wear value |
由图 2可知各个自变量对磨损量的响应面开口向上,说明伴随每个单因素的增加,响应值减小,当响应值减小至极值后,随着自变量水平继续增大,从响应面的最低点和等值线可知,在选取的范围内存在极值,即为响应曲面的最低点。利用Design Expert 7.0软件Optimization中Numerical功能可求解模型的最优化值。表 6是优化结果中的前10组数据,其中第1组为最优结果。通过对前10组数值的分析可知,钢纤维长径比A=56.24;体积掺入率B=1.34%;水胶比C=0.37,在此条件下模型的响应值理论磨损量Y=75.153 9 g。
以最优化结果中的A,B,C为试验条件进行3组平行试验,结果见表 7。平均磨损量为76.1 g,与最优化预测结果的偏差为1.26%,与理论最优化预测结果相近,这证明基于响应面分析法设计的钢纤维水泥混凝土耐磨性试验的拟合性和准确性。
| 编号 | 长径比A | 掺入率B/% | 水胶比C | 磨损量Y/g | 平均磨损量/g |
| 1 | 55.50 | 1.36 | 0.37 | 76.2 | 76.1 |
| 2 | 55.50 | 1.36 | 0.37 | 75.4 | |
| 3 | 55.50 | 1.36 | 0.37 | 76.7 |
在钢纤维混凝土的配合比中选择合适的钢纤维长径比、体积掺入率和水胶比可以使耐磨性优于普通混凝土,提高水泥混凝土路面的使用寿命,达到社会经济效益的要求;在影响钢纤维水泥混凝土耐磨性的3种主要因素中,影响次序为钢纤维长径比、水胶比和体积掺入率依次减弱;通过响应面分析法建立预测模型,得到钢纤维混凝土耐磨性的最佳组合:钢纤维长径比为56.24,钢纤维掺入率为1.34%,水胶比为0.37,理论磨损量为75.2 g。验证磨损量为76.1 g,与理论值差异不大,也证明响应面分析法设计的准确性与科学性。
| [1] | 邵旭东,王文前,辜杰凯,等. 装配式纤维混凝土组合桥面体系试验[J]. 公路交通科技,2013,30(6):60-66. SHAO Xu-dong,WANG Wen-qian,GU Jie-kai,et al. Experiment on Assembled Composite Bridge Deck System Composed of Fiber Concrete [J]. Journal of Highway and Transportation Research and Development,2013,30(6):60-66. |
| [2] | 徐强,杜进生,张劲泉. 活性粉末混凝土受压力学性能试验[J]. 公路交通科技,2011,28(7):8-13. XU Qiang,DU Jin-sheng,ZHANG Jin-quan. Experiment of Mechanical Properties of Reactive Powder Concrete in Compression[J]. Journal of Highway and Transportation Research and Development,2011,28(7):8-13. |
| [3] | 付智,李红.纤维混凝土路面施工技术[J].公路,2011,28(1):36-46. FU Zhi,LI Hong. Construction Technology of Fiber Concrete Pavement[J].Highway,2011,28(1):36-46. |
| [4] | 王军龙,肖建庄.钢纤维再生混凝土的抗折强度试验研究[J]. 工业建筑,2007,37 (1):82-86. WANG Jun-long,XIAO Jian-zhuang. Investigation on the Test of Flexural Strength of Steel Fiber Recycled Concrete[J]. Industrial Construction,2007,37(1):82-86. |
| [5] | 邓宗才,薛会青,刘爱军. 纤维素纤维及混杂纤维混凝土的抗弯冲击性能[J]. 北京工业大学学报,2008,34(11):1149-1153. DENG Zong-cai,XUE Hui-qing,LIU Ai-jun. Flexural Impact Behavior of Cellulose and Hybrid Fibers Reinforced Concrete Beams[J]. Journal of Beijing University of Technology,2008,34(11):1149-1153. |
| [6] | 王永菲,王成国. 响应面法的理论与应用[J]. 中央民族大学学报:自然科学版,2005,14 (3):236-240. WANG Yong-fei,WANG Cheng-guo. The Application of Response Surface Methodology[J]. Journal of Minzu University of China :Natural Science Edition,2005,14 (3):236-240. |
| [7] | HRYNYK T D,VECCHIO F J. Behavior of Steel Fiber-reinforced Concrete Slabs under Impact Load[J]. ACI Structural Journal,2014,42(111):1-6. |
| [8] | 赵顺波,杜晖,钱晓军,等. 钢纤维高强混凝土配合比直接设计方法研究[J]. 土木工程学报,2008,41 (7):1-6. ZHAO Shun-bo,DU Hui,QIAN Xiao-jun, et al. Study on Direct Mix Design Method for Steel Fiber Reinforced High-strength Concrete[J]. China Civil Engineering Journal,2008,41 (7):1-6. |
| [9] | AGGELIS D G,SOULIOTI D V,BARKOULA N M,et al. Influence of Fiber Chemical Coating on the Acoustic Emission Behavior of Steel Fiber Reinforced Concrete[J]. |
| [10] | JTG E30—2005,公路工程水泥及水泥混凝土试验规程[S]. JTG E30—2005,Test Methods of Cement and Concrete for Highway Engineering [S]. |
| [11] | VANCURA M,KHAZANOVICH L,TOMPKINS D. Reappraisal of Recycled Concrete Aggregate as Coarse Aggregate in Concretes for Rigid Pavements[J]. |
| [12] | 陈瑜,周士琼.道路粉煤灰高性能混凝土耐磨性试验研究[J].公路,2000,11(11):49-53. CHEN Yu,ZHOU Shi-qiong. Experimental Study of Abrasion Resistance of Road High Performance Concrete with Fly Ash [J].Highway,2000,11(11):49-53. |
 2015, Vol. 31
2015, Vol. 31