扩展功能
文章信息
- 康永刚, 张秀娥, 张华明
- KANG Yong-gang, ZHANG Xiu-e, ZHANG Hua-ming
- 沥青混合料蠕变的变参数模型
- Variable-parameter Creep Model of Asphalt Mixture
- 公路交通科技, 2015, Vol. 31 (7): 13-17
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (7): 13-17
- 10.3969/j.issn.1002-0268.2015.07.003
-
文章历史
- 收稿日期:2013-09-09
2. 山西省雷电防护监测中心, 山西 太原 030002
2. Thunder Prevention and Monitoring Center of Shanxi Province, Taiyuan Shanxi 030002, China
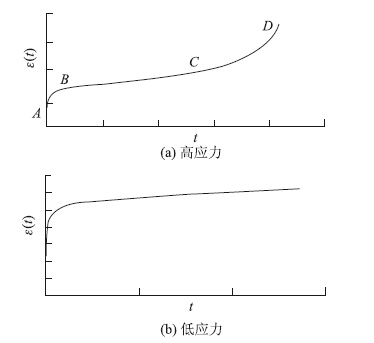
沥青混合料是一种黏弹性材料,在应力比较大的荷载作用下,或由于高温而超过其极限承载能力时,其蠕变过程可分为迁移期、稳定期和破坏期3个阶段,分别对应于图 1(a)中AB,BC,CD段[1, 2],其中ε(t)表示应变,t表示时间。迁移期,变形迅速增大,但应变速率随时间增加逐渐减小;稳定期,应变稳定增长,但应变速率基本保持不变;破坏期,应变、应变速率随时间增加迅速增大直至破坏。另一类是在应力比较小的荷载作用下的蠕变,黏性流动变形并不随荷载作用时间的延长而无限增加,而是随着时间的推移,黏性流动变形的增量逐渐减小,最终使黏性流动变形趋于一个稳定值,表现出一种固结效应,蠕变曲线只有迁移期和稳定期两个阶段,如图 1(b)所示[2]。
|
| 图 1 沥青混合料的蠕变曲线 Fig. 1Creep curves of asphalt mixture |
目前对沥青混合料黏弹性本构关系的研究较多,提出了各种黏弹性本构模型,如Kelvin模型、Maxwell模型、标准线性固体模型、Burgers 模型以及广义Kelvin 模型、广义Maxwell 模型等[3, 4]。Judycki[5]对常规和改性沥青混凝土在蠕变试验条件下的非线性黏弹性行为进行了研究,建立了一个非线性黏弹性模型;郑健龙[6]建立了沥青混合料热黏弹性本构模型;徐世法[7]采用黏弹性理论,提出了一个四单元五参数模型来分析沥青路面的永久变形;王后裕[8]通过分析沥青混合料加载时的固结效应和卸载时的永久变形等流变学特征,提出了一个流变学模型。但是,以上这些模型只能描述前两个蠕变阶段。
近些年,建立能描述沥青混合料3个蠕变阶段的模型成为研究重点[9, 10, 11, 12, 13]。如从损伤力学角度出发:张久鹏[9]以流变学模型理论为基础,综合考虑损伤和硬化效应,建立了一个统一的沥青混合料损伤蠕变模型,但该模型参数过多。曾国伟[11]在三元件模型基础上耦合一个连续性损伤因子,构建一个能够描述沥青混合料蠕变全过程的损伤蠕变模型。冯林[12]提出了一种黏-弹-塑本构模型,并采用Kachanov蠕变损伤律进行全局耦合。从力学元件的非线性化角度出发:张久鹏[10]对Burgers 模型中的弹簧进行改进,认为其弹性模量随应变增大而减小,但没有考虑黏性元件的非线性。叶永[13]采用多种岩石蠕变模型来描述沥青混合料的蠕变,这些模型仅对描述第3个阶段的元件进行非线性化,并且包含元件较多,相应参数也较多。
Zener模型是重要的黏弹性模型,被称为标准线性固体模型,对黏弹性材料的应力松弛、蠕变都可以定性描述。本文从力学元件的非线性化角度出发,用变参数黏壶替换Zener模型中的黏壶,构造出变参数Zener模型,推导出它的本构方程和蠕变函数。改进后的模型串联一个变参数黏壶适合描述沥青混合料的整个蠕变过程,并且相对同类模型,其包含相对较少的元件,相应的参数也较少。 1 变参数Zener模型
经典弹簧的应力σ(t)和应变ε(t)满足虎克定律σ(t)=Eε(t), 其中t表示时间;E表示弹性模量。经典的黏壶满足牛顿定律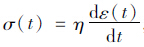 , 其中η表示黏滞系数。Zener模型是一个Maxwell模型(一个弹簧和一个黏壶的串联)并联一个弹簧的结构,对黏弹性材料的应力松弛、蠕变都可以定性描述,但要准确地描述黏弹过程,需要比较复杂的模型。
, 其中η表示黏滞系数。Zener模型是一个Maxwell模型(一个弹簧和一个黏壶的串联)并联一个弹簧的结构,对黏弹性材料的应力松弛、蠕变都可以定性描述,但要准确地描述黏弹过程,需要比较复杂的模型。
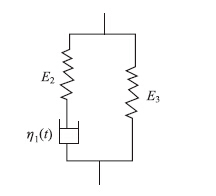
建立变参数模型的出发点是,在应力作用下,材料的微观结构发生改变,其中某些力学参数随着时间的变化而变化,需要考虑力学参数的时间效应。在此引入一个变参数的黏壶:
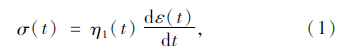
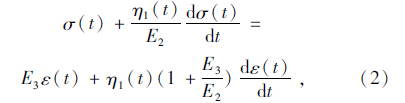
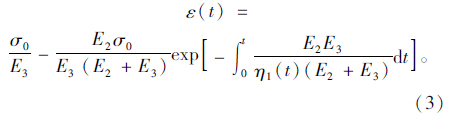
|
| 图 2 变参数Zener模型 Fig. 2Variable-parameter Zener model |
徐世法[7]提出的四单元五参数模型,即一个改进的Burgers模型,它取串联黏壶的黏滞系数为η(t)=AeBt来反映沥青混合料的固结效应。设黏滞系数随时间幂律变化:

式中,η10,α为常数且α>0,α≠0。当0<α<1时,表示黏滞系数随时间增加;当α>1时,表示黏滞系数随时间减小。但是时间趋于零时,α>1会导致黏滞系数趋于无穷,所以表示黏滞系数随时间的减小,应采用其他形式,如η(t)=η10(t+C)1-α,其中α>1,C为常数且C>0。在此取0<α<1,即黏滞系数随时间幂律增加来表示固结效应,所以下面仍然以式(4)为例讨论。把式(4)代入式(3)得到:
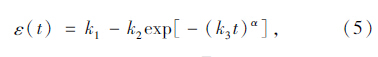
式中,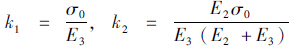 和k3=
和k3=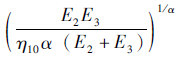 。式(5)中的exp-(k3t)α称为stretched exponential函数,张为民用该函数给出的蠕变柔量实用表达式,与式(5)形式相同[14]。当t→∞时,式(5)的应变趋于稳定值k1。
。式(5)中的exp-(k3t)α称为stretched exponential函数,张为民用该函数给出的蠕变柔量实用表达式,与式(5)形式相同[14]。当t→∞时,式(5)的应变趋于稳定值k1。
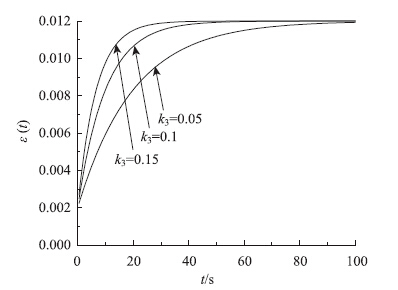
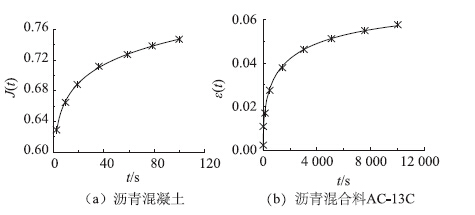
图 3是变参数Zener模型式(5)的蠕变曲线(k3取不同值),参数分别为k1=0.012,k2=0.01和α=0.8。可见,变参数Zener模型的蠕变只有迁移期和稳定期两个阶段,是应力比较小的荷载作用下的蠕变模型。图 4(a)为单轴贯入试验获得的沥青混凝土的蠕变柔量[15]。注意:蠕变时常应力σ0、应变ε(t)和蠕变柔量J(t)满足ε(t)=σ0J(t)。图 4(b) 为25 ℃、静载为100 kPa 下沥青混合料AC-13C,通过UTM 进行室内静态蠕变试验的数据[16]。图 4中曲线为式(5)的拟合结果,拟合参数列于表 1,注意参数k1和k2为无量纲。
|
| 图 3 变参数Zener模型的蠕变曲线 Fig. 3Creep curves of variable-parameter Zener model |
|
| 图 4 蠕变试验数据及式(5)拟合曲线 Fig. 4Creep test data and fitting curves of Eq.(5) |
| k1 | k2 | k3/s-1 | α | |
| Fig. 4(a) | 2.639σ0 | 2.32σ0 | 0.130 | 0.098 |
| Fig. 4(b) | 0.067 1 | 0.067 1 | 0.042 4 | 0.414 |
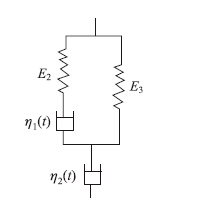
变参数Zener模型无法描述破坏期的情形,需要对它进行改进。在此,通过串联一个描述第3阶段蠕变的变参数黏壶η2(t),如图 5所示,给出适合描述整个蠕变过程的模型。力学元件串联时应力相同,合应变为各并联单元应变之和,蠕变函数一般表达式为:
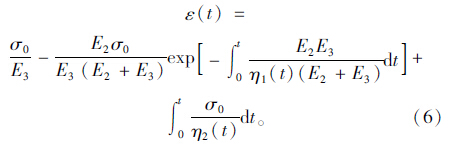
张久鹏[17]假设黏滞系数是先增大后减小,作如下改进:
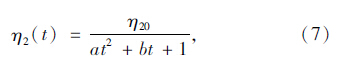
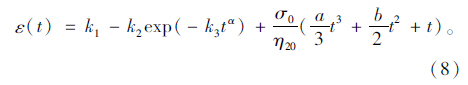
|
| 图 5 改进的变参数Zener模型 Fig. 5Improved variable-parameter Zener model |
为了描述蠕变第3阶段破坏期,根据此阶段的特点,在此假设串联黏壶的黏滞系数随时间指数减少为:
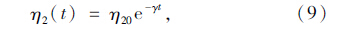
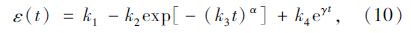
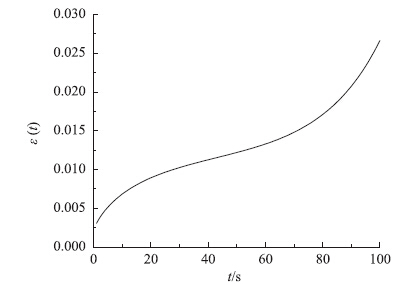
图 6是改进的变参数Zener模型式(10)的蠕变曲线,参数分别为k1=0.012,k2=0.01,k3=0.1,k4=0.000 1,α=0.8和γ=0.05。可见,改进的变参数Zener模型的蠕变有3个阶段,是应力比较大的荷载作用下的蠕变模型。沥青混合料种类和蠕变条件的多样性,黏壶η2(t)的蠕变函数也可取其他形式,如幂律型σ0η20tm,幂律指数型σ0η20tmeβt等,对应的黏滞系数很容易反推出。
|
| 图 6 变参数Zener模型的蠕变曲线 Fig. 6Creep curve of variable-parameter Zener model |
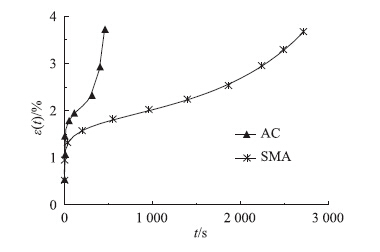
图 7为张久鹏[9]等人在UTM试验机上分别进行SMA13和AC13两种类型沥青混合料的单轴静载蠕变试验。为加快蠕变试验进程,试验荷载为0.7 MPa,试验温度为60 ℃。SMA13采用SBS改性沥青,AC13采用AH70#普通沥青,混合料的级配、油石质量比详见文献[17]。图 7中曲线为式(10)的拟合结果,以后计划开展模型参数的识别研究,本文对试验数据进行分段拟合:由于非定常黏壶η2(t)对蠕变的前两个阶段影响较小,首先用最小二乘法和式(5)拟合前两个阶段的数据(AC取t<210 s,SMA取t<1 000 s),得到参数k1,k2,k3和α的值;保持这些参数值不变,用式(10)拟合所有试验数据得到参数k4和γ,拟合参数列于表 2,注意参数k1,k2和k4为无量纲。
|
| 图 7 蠕变试验数据及式(10)拟合曲线 Fig. 7Creep test data and fitting curves of Eq.(10) |
| k1 | k2 | k3/s-1 | k4 | α | γ | |
| AC | 0.022 5 | 0.016 | 0.034 | 0.000 040 | 0.40 | 0.013 |
| SMA | 0.032 7 | 0.029 | 0.000 105 | 0.000 98 | 0.20 | 0.001 05 |
在应力作用下,材料的微观结构发生改变,其某些力学参数随着时间的变化而变化,需要考虑力学参数的时间效应。用变参数黏壶替换Zener模型中的黏壶,构造出变参数Zener模型,推导出它的本构方程和蠕变函数。改进后的模型串联一个描述第3阶段蠕变的变参数黏壶,适合描述沥青混合料整个蠕变过程。用所建立的模型分别拟合不同的蠕变试验数据,都给出较好的描述。
| [1] | WITCZAK M W,KALOUSH K,PELLINEN T.Simple Performance Test for Superpave Mix Design,NCHRP Report 465 [R]. Washington,D. C.:National Academy Press,2002. |
| [2] | 詹小丽,张肖宁,王端宜,等. 改性沥青非线性粘弹性本构关系研究及应用[J]. 工程力学, 2009, 26(4):187-191. ZHAN Xiao-li,ZHANG Xiao-ning,WANG Duan-yi,et al. Study on Nonlinear Viscoelastic Constitutive Equation of Modified Asphalt and Its Applications[J]. Engineering Mechanics, 2009,26(4):187-191. |
| [3] | 周志刚,刘飞,冯林. 优化理论的沥青混合料蠕变本构模型经验性公式[J].长沙理工大学学报:自然科学版,2009,6(1):6-9. ZHOU Zhi-gang,LIU Fei,FENG Lin. Experienced Equation of Asphalt Mixture Creep Constitutive Model Based on Optimization Theory[J].Journal of Changsha University of Science and Technology:Natural Science Edition,2009,6(1):6-9. |
| [4] | 闵召辉,黄卫,钱振东. 环氧沥青蠕变力学模型研究[J]. 公路交通科技,2008,25(12):71-75. MIN Zhao-hui,HUANG Wei,QIAN Zhen-dong. Analysis on Creep Mechanical Model of Epoxy Asphalt[J]. Journal of Highway and Transportation Research and Development,2008,25(12):71-75. |
| [5] | JUDYCKI J. Nonlinear Viscoelastic Behaviour of Conventional and Modified Asphaltic Concrete under Creep[J]. |
| [6] | 郑健龙,田小革,应荣华. 沥青混合料热粘弹性本构模型的实验研究[J].长沙理工大学学报:自然科学版,2004,1(1):1-7. ZHENG Jian-long,TIAN Xiao-ge,YING Rong-hua. A Laboratory Research on the Thermo-viscoelastic Constitutive Model of Bituminous Mixtures[J].Journal of Changsha University of Science and Technology:Natural Science Edition,2004,1(1):1-7. |
| [7] | 徐世法,朱照宏. 高等级道路沥青路面车辙的预估方法[J]. 土木工程学报,1993,26(6): 28-36. XU Shi-fa,ZHU Zhao-hong. Prediction of Rutting in Asphalt Pavement of High-class Road[J]. China Civil Engineering Journal,1993,26(6): 28-36. |
| [8] | 王后裕,朱可善,言志信,等.沥青混合料蠕变柔量的一种实用模型及其应用[J]. 固体力学学报,2002,23(2):232-236. WANG Hou-yu,ZHU Ke-shan,YAN Zhi-xin,et al. A Practical Creep Compliance Model of Asphalt Mixtures and Its Application[J]. Acta Mechanica Solida Sinica,2002,23(2):232-236. |
| [9] | 张久鹏,黄晓明,马涛. 沥青混合料损伤蠕变特性及模型研究[J]. 岩土工程学报,2008,30(12):1867-1871. ZHANG Jiu-peng,HUANG Xiao-ming,MA Tao. Damage-creep Characteristics and Model of Asphalt Mixture[J]. Chinese Journal of Geotechnical Engineering,2008,30(12):1867-1871. |
| [10] | 张久鹏,黄晓明,高英. 沥青混合料非线性蠕变模型及其参数确定[J]. 长安大学学报:自然科学版,2009,29(2):24-27,55. ZHANG Jiu-peng,HUANG Xiao-ming,GAO Ying. Nonlinear Creep Model of Asphalt Mixture and Parameter Determination[J]. Journal of Chang'an University:Natural Science Edition,2009,29(2):24-27,55. |
| [11] | 曾国伟,杨新华,尹安毅,等.沥青混合料损伤蠕变模型试验研究[J]. 武汉科技大学学报, 2011,34(5):364-367. ZENG Guo-wei,YANG Xin-hua,YIN An-yi,et al. Experimental Researches on Damage Creep Model of Asphalt Mixture[J]. Journal of Wuhan University of Science and Technology,2011,34(5):364-367. |
| [12] | 冯林. 单轴压力下沥青混合料静动态蠕变模型研究[D]. 长沙:长沙理工大学,2008. FENG Lin. Research on Static and Dynamic Creep Model of Asphalt Mixture under Uniaxial Pressure[D]. Changsha:Changsha University of Science & Technology,2008. |
| [13] | 叶永. 沥青混合料粘弹塑性本构模型的实验研究[D]. 武汉:华中科技大学,2009. YE Yong. Experimental Researche on Viscoelastoplastic Constitutive Model of Asphalt Mixture[D]. Wuhan:Huazhong University of Science and Technology,2009. |
| [14] | 张为民.松弛模量与蠕变柔量的实用表达式[J]. 湘潭大学自然科学学报,1999,21(3):26-28. ZHANG Wei-min. Practical Expressions of Relaxation Modulus and Creep Compliance[J]. Natural Science Journal of Xiangtan University,1999,21(3):26-28. |
| [15] | 陈静云,周长红,王哲人.沥青混合料蠕变试验数据处理与粘弹性计算[J]. 东南大学学报:自然科学版,2007,37(6):1091-1095. CHEN Jing-yun,ZHOU Chang-hong,WANG Zhe-ren. Data Processing and Viscoelastic Computation for Creep Test of Asphalt Mixture[J]. Journal of Southeast University:Natural Science Edition,2007,37(6):1091-1095. |
| [16] | 范兵. 沥青混合料粘弹特性分析[J]. 路基工程,2009,30(5):151-152. FAN Bing. Analysis for Viscoelasticity of Asphalt Mixture[J]. Subgrade Engineering,2009, (5):151-152. |
| [17] | 张久鹏,徐丽,王秉纲. 沥青混合料蠕变模型的改进及其参数确定[J]. 武汉理工大学学报:交通科学与工程版,2010,34(4):699-702,706. ZHANG Jiu-peng,XU Li,WANG Bing-gang. Modification of Creep Model of Asphalt Mixture and Parameters Determination[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition,2010,34(4):699-702,706. |
 2015, Vol. 31
2015, Vol. 31
