扩展功能
文章信息
- 杨泳, 严余松, 户佐安, 古沐松
- YANG Yong, YAN Yu-song, HU Zuo-an, GU Mu-song
- 城市快速路改进型元胞传输模型及仿真
- An Improved Cell Transmission Model for Urban Expressway and Simulation
- 公路交通科技, 2015, Vol. 31 (6): 135-141
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (6): 135-141
- 10.3969/j.issn.1002-0268.2015.06.021
-
文章历史
- 收稿日期:2014-07-11
2. 西南交通大学 信息科学与技术学院, 四川 成都 610031
2. School of Information Science and Technology, Southwest Jiaotong University, Chengdu Sichuan 610031, China
近年来,交通流已成为一个多学科交叉研究的热点课题。由于交通流呈现出许多非平衡、非线性特征,如交通流相变、交通激波、同步流、交通滞后、时走时停等现象,人们提出了许多交通流模型从理论上研究这些问题。交通流模型通过描述流量、速度、密度之间的关系来解释交通运行的基本性质和运行规则。交通流模型的选择应能合理、准确地描述交通流的特性,特别是在拥堵情况下的交通流变化特点。Daganzo[1, 2] 于1994年通过简化交通流量和密度间的关系,采用有限微分法建立了交通传输模型 (cell Transmission Model,CTM),用于模拟高速公路上的交通流。20世纪中叶,Lighthill、Whitham和Richards分别对连续交通流模型进行了研究,提出了一阶宏观连续交通流模型,即LWR模型[3]。元胞传输模型不仅是对LWR模型[3]或流体力学理论的收敛和逼近,更重要的是它对实际路网提供了一种简单的求解方法,因此CTM模型是一种目前公认的交通流模型和模拟动态交通的技术手段。
CTM模型能够清晰地描述排队的物理效应以及一些交通流动力学特性,对于描述波动较大的交通流特性有相当优势。盛慧等[4]通过引入元胞长度参数提出了改进型CTM模型,并用于城市道路的交通预测。曾建勤[5]等应用CTM模型对城市干道交通流进行建模,并对信号周期、绿信比和相位差等交通控制方法进行了优化,取得了较为满意的结果。袁长亮等[6]在改进型CTM模型的基础上,针对快速路出口匝道系统采用定时控制策略进行了系统研究。龙建成[7]在Daganzo研究的基础上,构建了考虑交通流回滞现象的CTM路段模型,针对路段下游渠化长度、停止线宽度、事故位置及路段长度等因素对交通拥堵传播的影响,研究了城市道路交通拥堵的传播规律。
城市快速路进/出口匝道分布不均匀的特点,造成了建立相同长度元胞的困难,因此提出可变宽度元胞传输模型。在此基础上,针对传统CTM模型采用的梯形或三角形的流量-密度函数近似处理无法描述交通的同步流状态,难以表达拥堵交通时走时停,忽慢忽快的特点,本文引入Kerner三相流理论构造新的基本图模型考虑交通迟滞现象,并给出相应的元胞传输模型,通过实例仿真验证模型的有效性。
1 经典元胞传输模型
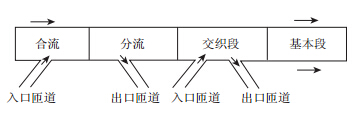
城市快速路拓扑结构如图 1所示,包括基本段、合流段、分流段及交织段4种典型模式。根据是否连接出入口匝道以及车辆在路段端点处的运动方向,将车流在快速路上的运动形式简化为无匝道连接的直线运动(基本段)、有入口匝道的合流运动、有出口匝道的分流运动。CTM模型对路段分段研究,能够充分兼顾交通流的微观特性,关注小群体车辆间的交通流状态传递过程,对畅通流、拥挤流及堵塞交通流均有良好的描述效果。
|
| 图 1 城市快速路拓扑结构示意图 Fig. 1 Schematic diagram of topological structure of urban expressway |
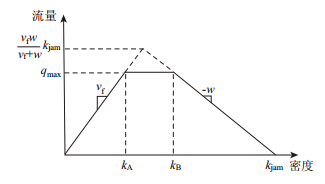
CTM模型假定流量和密度的关系服从梯形形式的函数,如图 2所示。假定在低密度的交通状况时,自由流速度是一个常量vf; 在高密度的交通状况时,车流波的反向传播速度是常量w,且通常满足w<vf。实际上,CTM模型适用于任何流量-密度关系,梯形函数形式是其中一种比较常见且通用的简化应用形式。对大量高速公路的交通调查表明,在中低密度范围内,道路的通行能力是基本稳定的,基本符合梯形函数形式。
|
| 图 2 CTM模型中梯形流量-密度关系 Fig. 2 Ladder-shaped volume-density relation in CTM model |
图 2中任意时刻的流量-密度关系可以表示为:
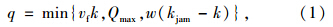
1.1 CTM基本段模型
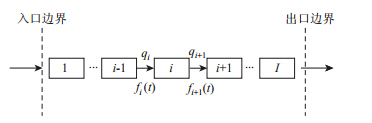
图 3为CTM模型基本段元胞模型空间示意图。从道路的上游连续标识这些单位,即元胞1到元胞I。
|
| 图 3 CTM模型基本段元胞示意图 Fig. 3 Schematic diagram of basic module cells in CTM model |
依据连续交通流理论(LWR理论)的元胞间流量连续守恒原理,对时间、空间分别进行离散化处理,建立CTM模型的基本段模型:
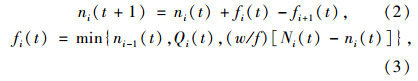
模型可以很好地适用于拥堵状态和非拥堵状态。当交通需求较小时,流入元胞i内的实际车辆数fi(t)等于上游元胞i-1的车辆数ni-1(t);当交通拥堵时,fi(t)等于元胞i的剩余可容纳车辆数;当元胞i成为交通瓶颈时,fi(t)等于t时刻可以进入元胞i的最大车辆数Qi(t)。
定义发送能力Si(t)和接受能力Ri(t)分别为第t个时间间隔内元胞i所能发出的车辆数和所能接收的车辆数。其公式为:
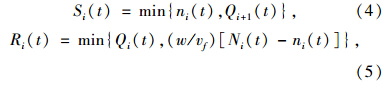
则第t个时间间隔内流入元胞i内的车辆数由上游元胞 i-1的发送能力和当前元胞i的接收能力共同决定。则式(3)可简化为:
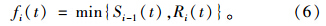
式(2)和式(4)~(6)一起构成了CTM基本段模型。
1.2 CTM合流段模型
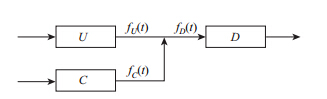
如图 4所示,令快速路上游主路元胞为U,匝道入口元胞为C,下游主路元胞为D。第t个时间间隔内,设元胞U的流出车流量为fU(t),元胞U的发送能力和接收能力分别为SU(t)和RU(t),元胞C的流出车流量为fC(t)SC(t)和RC(t),元胞D的流入车流量为fD(t),元胞D的接收能力和接收能力分别为SD(t)和RD(t)。
|
| 图 4 CTM模型合流段元胞示意图 Fig. 4 Schematic diagram of merging cell modules in CTM model |
根据元胞发送能力和接收能力的定义,在入口匝道的快速路合流点处,上游元胞流出车流量和下游元胞流入车流量需满足元胞发送能力和接收能力的限制:
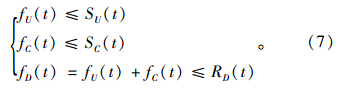
根据下游元胞D的接收能力是否充足,合流段模型可以分成两种情况。
(1)若RD(t)≥SU(t)+SC(t),有:
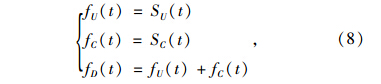
(2)若RD(t)<SU(t)+SC(t),则有:
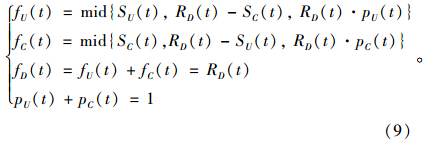
下游元胞D的接收能力(供给)不充足,并不能满足上游主路元胞U和匝道入口元胞C的所有交通发送量(需求),此时,上、下游处于拥堵或者部分拥堵状态,交通流量由下游决定。而上游主路元胞U和匝道入口元胞C的流出量则由两者的发送能力、下游元胞D接收能力以及两者的优先权重或车流比例共同决定。式(9)中,pU(t)和pC(t)分别为上游主路元胞U和匝道入口元胞C向下游元胞D流入的车流比例,也代表了两股交通流的融合比率。在实际的交通模拟中,可以通过实时调整两个比例参数的取值,实现快速路匝道控制模拟。
式(2)、式(6)、式(8)和式(9)一起构成了CTM合流段模型。
1.3 CTM分流段模型
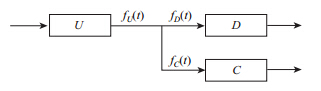
同理,如图 5所示,设快速路上游主路元胞为U,下游主路元胞为D,下游匝道出口元胞为C。第t个时间间隔内设元胞U的流出车流量为 fU(t),元胞U的发送能力和接收能力分别为SU(t)和RU(t),元胞D的流入车流量为fD(t),元胞D的发送能力和接收能力分别为SD(t)和RD(t),元胞C的流入车流量为fC(t),元胞C的发送能力和接收能力分别为SC(t)RC(t)。
|
| 图 5 CTM模型分流段元胞示意图 Fig. 5 CTM diverged module cell diagram |
根据元胞发送能力和接收能力的定义,在出口匝道的快速路分流点处,上游元胞流出车流量和下游元胞流入车流量需满足元胞发送能力和接收能力的限制:
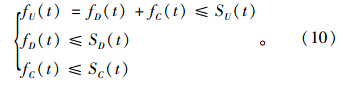
假定在快速路匝道分流点处从上游主路元胞U流入下游主路元胞D的车流比率为γD(t),流入下游匝道出口元胞C的车流比率为γC(t),则:
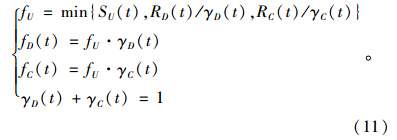
式(2)、式(6)和式(9)一起构成了CTM合流段模型。
2 改进元胞传输模型 2.1 可变元胞模型 (Variable CTM,VCTM)
城市快速路几何长度较短且长短不一,进出口匝道间距并不规则,造成CTM模型需要根据不同路段长度建立不同长度的元胞。与CTM选取元胞i内的车辆数ni(t)作为元胞状态变量不同,VCTM以元胞内的车辆密度ki(t)作为状态变量,这种改进去除了CTM对于每个元胞长度必须相等的限制。
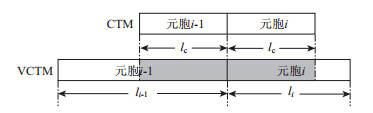
如图 6所示,设第i元胞长度为li,元胞长度li和li+1均不小于车辆在一个时间步长内以自由流的速度通过的距离Lc。
|
| 图 6 CTM模型和MCTM模型元胞示意图 Fig. 6 Schematic diagram of cells in CTM and MCTM |
在单位时间步长ε内,VCTM模型的上游元胞i-1 的驶出车辆数仅与该元胞后半段长度Lc内的车辆数和从模型的上游元胞 i-1驶入元胞i的最大车辆数有关,而驶入下游元胞i的车辆数仅与该元胞前半段Lc长度内的车辆数和最大驶入车辆数有关。则模型中元胞i的发送能力Si和接受能力Ri可表示为:
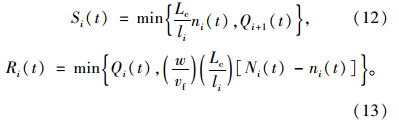
式(2)、式(6)、式(12)~(13)一起构成了VCTM基本段模型。此时,依然通过元胞内车辆数、元胞发送量、元胞接收量等表征元胞状态,这在元胞长度固定时是可行且直观的,但在元胞长度变化情况下并不合适,因此需要引入交通流密度、元胞发送流率、元胞接收流率等元胞状态进行充分描述。
进一步离散元胞守恒方程后可得:
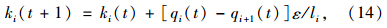
式(14)反映了VCTM模型元胞的基本交通流传播特性,与式(2)的经典CTM模型并无本质区别。增加的元胞长度li和交通流密度ki(t)两个参数考虑更为全面,有助于VCTM模型在不规则道路网中的应用:(1)VCTM模型引入了参数元胞长度li,使模型可根据路段长度确定元胞长度,元胞不必受到统一长度的限制;(2)VCTM模型引入的交通流密度ki(t)更容易描述交通流状态,也更便于交通流检测设备采集。
式(6)、式(12)、式(13)~(14)一起构成了可变元胞VCTM基本段模型,而合流段模型和分流段模型不变。
2.2 考虑迟滞现象的VCTM
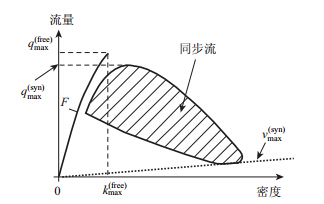
Nagel[8] 和Kerner[9, 10] 等人通过现场实测数据发现流量-密度关系的数据分布不同于传统线性或非线性理论,因此提出了三相交通流理论。该理论认为,随着车流密度的增加,自由流状态车辆之间的相互作用逐渐增强,流量-密度(q-k)关系的表述会变得越来越复杂。在拥挤状态下,分布在一个较大的二维区域中,很难用一个函数关系式来描述,如图 7所示。其中q(free)max是指自由流状态下的流量最大值;k(free)max是对应自由流状态最大流量下的密度值;q(syn)max是同步流状态下的流量最大值;v(syn)min是同步流状态下速度最小值。自由流区与拥挤区不是完全孤立的,两者之间存在着相互重叠的部分,这一区域成为亚稳态区。在该区域内,车流有可能处于自由流状态,有可能处于拥挤状态。亚稳态区域的存在导致了迟滞现象的发生,即自由流到拥挤流相变时的车流密度往往高于拥挤流到自由流相变的车流密度[11],而迟滞现象在传统基本图上几乎无法正确解释。
|
| 图 7 Kerner交通基本图 Fig. 7 Kenner's fundamental traffic curves |
元胞传输模型是由LWR理论离散并求解该模型得到的,模型的基本假设是流量与密度服从连续 (三角形或梯形)形式的函数关系,导致模型具有一些固有缺陷。模型的主要固有缺陷在于描述拥挤路段上的车流传播时会引起较大误差,而迟滞环反映了自由流和拥挤流之间的转换关系,是典型的交通现象之一,普遍存在于当前日益拥挤的城市快速路交通流中。
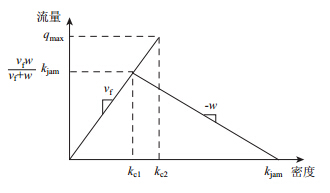
考虑迟滞现象的流量-密度基本图如图 8所示。
|
| 图 8 考虑迟滞现象的CTM流量-密度基本图 Fig. 8 Fundamental volume-density diagram of CTM with hysteresis characteristics |
根据该图,有:
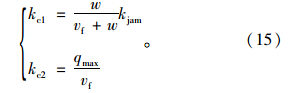
在图 8范围内,车流有自由流、拥挤流两种交通状态。自由流向拥挤流转变的车流密度为kc2,而拥挤流向自由流转变的车流密度为kcl,显然满足kc1 元胞的发送能力既受元胞上的车流密度限制,又受下游元胞的流出能力限制;而元胞的接收能力则主要取决于元胞的车流状态,如果元胞上的车流处于自由流,则该元胞的接收能力取决于元胞的最大流率,否则其接收能力取决于元胞的车流密度。
进一步可以推导出元胞发送能力Si(t)和接收能力Ri(t)的表达式为:
式(14)、式(16)、式(17)和式(18)一起构成了考虑迟滞现象的VCTM基本段模型,而合流段模型和分流段模型不变。
依据传统的交通波基础理论,波速公式为:
3 算例分析
3.1 算例说明
采用上述构建的改进型元胞传输模型进行仿真。仿真对象选取成都市一段典型的高架城市快速路路段,仿真路段长2.53 km,单向2车道,包括1个入口匝道和1个出口匝道,分别位于起始端的0.95 km和1.55 km处。快速路通行能力5 400 veh/h,最初交通流达到80%通行能力时车流不受干扰稳定流动。从第11个模拟时间步上,距路段起始端1.25 km处发生一起交通事件,导致该处通行能力下降至30%,事件持续约3 min。用修改前的CTM模型计算车流波的反向传播速度w约为25 km/h,据此设置算例中的拥挤波速。
将该路段划分成以下9个元胞(各元胞的长度为li,i=1,2,…,9):
{300,300,300,250,230,250,300,300,300}。
模拟元胞示意图如图 9所示,共包括9个元胞、1个虚拟输入元胞、1个虚拟输出元胞。其中,元胞6包含一出口匝道,形成分流路段。本算例中假定分流匝道有足够的接收空间,元胞接收能力为无限大,分离比为10%,即有R出口匝道(t)=∞ 和γ出口匝道(t)=10%。而元胞4包含一入口匝道,形成合流路段,入口匝道交通流融合比率设置为50%,即有p入口匝道(t)=50%,入口匝道发送率设置为主道元胞发送率的20%。其他元胞均无出入口匝道,形成基本段。交通事故发生在元胞5,持续时间为15个模拟时间步。
模拟中的其他参数设置如下:
时间步长ε为12 s;
模拟时长为30 min,即150个时间步;
自由流速度vf为67.5 km/h;
阻塞密度kjam为133 veh/km·车道;
车道数nl为2。
3.2 算例分析
模型仿真后的结果如图 10、图 11所示,取编号为3,4,5,6这4个元胞分别代表合流元胞、基本段元胞、事故元胞和分流元胞。从图 10可以看出,事故发生时刻之前,各元胞交通流密度趋于稳定,其中元胞4,5,6在元胞3与元胞10上形成合流后交通流密度有所增加。
在第11个时间步中,元胞5上发生交通事件,通行能力下降至30%,由此引起下游元胞6的交通流密度迅速下降,而元胞5交通流密度开始增加,并向上游传播,下一个时刻(即第12个时间步),元胞5的交通流密度进一步上升,且其形成的拥堵车流以反向波速度向上游传递。从第14个时间步开始,其上游元胞4的交通流开始上升,第17个时间步中,元胞3的交通流逐步增加。第25个时间步中,元胞5上的交通事件清除,此时,元胞3,4,5交通流密度很大,形成拥堵元胞,而其下游形成自由流状态。随着事件的清除,元胞5的通行能力得到恢复,此时元胞5的交通流密度迅速下降,而下游元胞交通流密度迅速增加,形成的这种拥堵消散波以自由流速度迅速向上游传播,而在消散波传导至元胞3之前,其交通流密度仍呈现增长趋势(元胞21~ 27),元胞3,4,5分别用5,11,18个时间步才恢复至交通事件发生前的交通拥堵水平。通过式(19) 计算得到突发交通事件发生时刻元胞4、元胞5阵面形成的拥堵压缩波波速为25.62 veh/km,与算例中设置的w之间的误差小于3%。
进一步分析各元胞流入流出率随时间步的曲线关系。如图 11所示,交通事件发生后,上游元胞的流入率、流出率同时下降,且流入率的变化比流出率的变化缓慢,因此造成其交通流密度的上升,越靠近交通事件区域,其趋势越明显。相反地,下游元胞流出率的下降速度略小于流入率,因而导致交通流密度的下降,这些交通流现象与实际交通流状况非常接近。仿真结果表明,考虑迟滞现象的VCTM模型可以准确地模拟城市快速路系统的交通流动态特性,从而为进一步研究城市快速路交通拥堵机理提供模型基础。
4 结论
本文采用改进的Daganzo元胞传输模型建立了适用于城市快速路系统的交通流理论分析工具,将元胞交通流密度和元胞长度两个参数引入CTM模型,克服了元胞长度必须相等的局限性,提出了可变元胞传输模型 (VCTM),对基本段、合流段和分流段3种不同元胞连接方式建立了元胞交通流传输关系式。同时,将考虑迟滞现象的三相交通流理论取代经典CTM模型的简单线性交通流模型,进一步扩展了模型的适用性。通过典型城市快速路路段算例分析表明,考虑迟滞现象的VCTM模型可以基本准确地模拟城市快速路系统的交通流动态特性,为进一步研究城市快速路交通拥堵机理提供基础。

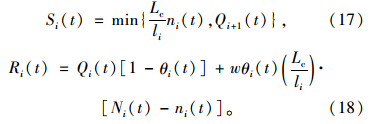
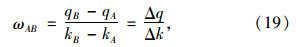
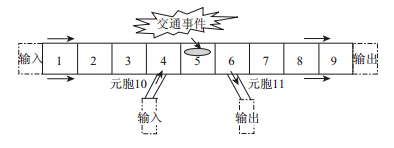
图 9 算例模拟路段元胞示意图
Fig. 9 Schematic diagram of road cellular in simulation case
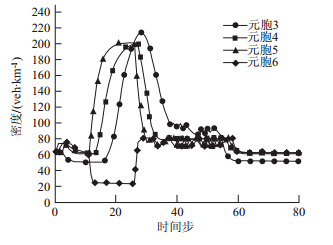
图 10 元胞3~元胞6时间-密度关系图
Fig. 10 Time-density relations of Cell 3-Cell 6
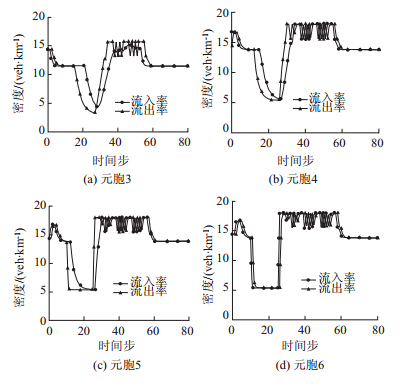
图 11 流入率和流出率
Fig. 11 Inflow rate and outflow rate
| [1] | DAGANZO C F. The Cell Transmission Model: A Simple Dynamic Representation of Highway Traffic [J]. |
| [2] | DAGANZO C F. The Cell Transmission Model, Part II: Network Traffic[J]. |
| [3] | LIGHTHILL M J, WHITHAM J B. On Kinematic Waves II: A Theory of Traffic Flow on Long Crowed Roads[J]. Proceedings of Royal Society of London. |
| [4] | 盛慧,王炜,胡晓健.基于改进型CTM模型的道路交通量预测 [J].公路交通科技,2009,26 (增1):49-52. SHENG Hui, WANG Wei, HU Xiao-jian. Traffic Volume Forecast Based on Improved Cell Transmission Model [J].Journal of Highway and Transportation Research and Development, 2009, 26(S1):49-52. |
| [5] | 曾建勤,王家捷,唐良,等.基于CTM-RH的城市交通信号线控制 [J].中国科学技术大学学报, 2006, 36(11):1232-1236. ZENG Jian-qin, WANG Jia-jie, TANG Liang, et al. CTM-RH Based Line Control for Urban Traffic Lights[J]. Journal of University of Science and Technology of China,2006,36(11):1232-1236. |
| [6] | 袁长亮, 李宏海.不同快速路出口设计通行能力条件下辅路信号控制策略研究[J]. 公路交通科技,2009,26(1):139-148. YUAN Chang-liang, LI Hong-hai. Study on Auxiliary Road Signal Control Strategy for Different Design Capacities of Expressway Exit[J]. Journal of Highway and Transportation Research and Development, 2009,26(1):139-148. |
| [7] | 龙建成.城市道路交通拥堵传播规律及消散控制策略研究[D].北京: 北京交通大学, 2009. LONG Jian-cheng. Study on Congestion Propagation Properties and Dissipation Control Strategies of Urban Road Traffic [D]. Beijing: Beijing Jiaotong University, 2009. |
| [8] | NAGEL K, WAGNER P, WOESLER R. Still Flowing: Approaches to Traffic Flow and Traffic Jam Modeling [J]. |
| [9] | KERNER B S. Three Phrase Traffic Theory and Highway Capacity [J]. |
| [10] | KERNER B S. Experimental Features of the Emergence of Moving Jams in Free Traffic Flow [J]. |
| [11] | YPERMAN I. The Link Transmission Model for Dynamic Network Loading [D]. Leuven, Belgium: Katholieke University, 2007. |
 2015, Vol. 31
2015, Vol. 31
