扩展功能
文章信息
- 王迎, 陈宽民, 周燕
- WANG Ying, CHEN Kuan-min, ZHOU Yan
- 基于TOPSIS模型的轨道交通线网评价
- Assessment of Rail Transit Network Based on TOPSIS Model
- 公路交通科技, 2015, Vol. 31 (6): 130-134
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (6): 130-134
- 10.3969/j.issn.1002-0268.2015.06.020
-
文章历史
- 收稿日期:2014-06-18
2. 天津城建大学 土木工程学院, 天津 300384
2. School of Civil Engineering, Tianjin Chengjian University, Tianjin 300384, China
轨道交通规划线网评价是轨道交通线网规划的关键环节,贯穿于轨道线网方案构架设计及评优决策的始终[1]。目前轨道交通线网评价多采用指标权重与评价函数相结合的方法,即在指标及其权重确定的前提下,通过构建评价函数用于分析指标的属性值,从而确定方案优劣排序。其核心思想是权重的计算和评价函数的选取[2, 3]。轨道交通线网评价方法有模糊评价法[4, 5, 6]、灰色关联度法[7, 8]、层次分析法[9]等,上述方法均存在一定缺陷。层次分析法过度依赖专家的主观判断,进行重要度分析时,客观信息考虑不足。相反,灰色关联度法主要依靠客观数据,缺乏考虑专家经验、决策者偏好等主观因素。模糊综合评价法需对所有评价方案进行全序排列,但由于专家本身理性的有限性及客观信息的复杂性,很难实现方案的合理全序排列[10, 11]。
本文提出了基于TOPSIS模型[12]的轨道交通线网评价方法。该方法充分考虑了主客观因素,采用AHP法与熵值法综合确定指标权重[13],使整个评价更加理性化、合理化,通过线网方案与理想方案距离比较,得到最优方案。
1 轨道交通线网评价指标体系评价轨道交通线网的前提是构建一个合理的评价指标体系。这一指标体系需全面反映线网结构、社会效益、可实施性等轨道交通特征属性及其延伸效用。我国多个城市如北京、上海、西安等都根据自身城市特点建立了轨道线网评价指标。本文在充分分析已有城市线网评价指标体系和查阅大量相关文献的基础上,本着目的性强、可测量、具有一定的灵敏度、合理和易操作的原则,从运营效果、网络结构、社会效益、战略发展、可实施性5方面提出了线网评价指标体系,见表 1。
| 目标层 | 准则层 | 指标层 |
|
轨道交通线 网最优方案 | 运营效果 | 线路负荷G1/[万人·(km·d)-1] |
| 断面不均匀系数G2 | ||
| 客运周转量G3/[万人·(km·d)-1] | ||
| 换乘系数G4 | ||
| 网络结构 | 覆盖中心面积率G5 | |
| 线网规模G6 /km | ||
| 客流集散点衔接数量G7 | ||
| 社会效益 | 轨道客流占公交客流比例G8 | |
| 节约公交出行时间G9 /(×104h·d-1) | ||
| 战略发展 | 城市土地利用协调程度G10 | |
| 沿线土地开发价值G11 | ||
| 城市景观协调程度G12 | ||
| 可实施性 | 工程难易程度G13 | |
| 近期线网可实施性G14 |
TOPSIS模型的基本思想是设定一个虚拟最优解(称为正理想解),它的各指标值都达到各备选方案中的最优值;一个虚拟最劣解(称为负理想解),它的各指标值都达到各备选方案中的最劣值。通过方案排序,即把各备选方案与正理想解和负理想解比较,若其中有一个方案最接近正理想解,则该方案为备选方案中的最优方案[14]。
轨道交通规划线网中,有n个规划方案,记为A=A1,A2,…,An; 有m个指标作为指标集,记为G=G1,G2,…,Gm。方案Ai对指标Gj的属性值为yij (i0=1,2,…,n;j=1,2,…,m),则初始决策矩阵为:

从表 1可见,评价指标体系分为成本型和效益型两大类,同时各指标量纲不同。为消除不同类型和不同量纲对评价结果的影响,需对指标进行归一化处理,建立标准化初始决策矩阵。
成本型指标归一化,令:
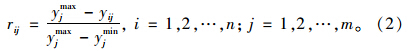
效益型指标归一化,令:

归一化处理后的标准决策矩阵为:
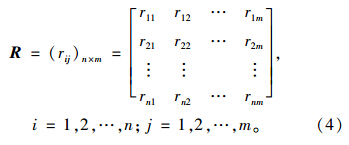
权重向量表示各优化目标在决策过程中所占的重要度。为使各优化目标权重更加客观、合理,本文综合考虑主、客观因素,应用AHP法和熵权法确定各优化目标权重。
(1)AHP法
AHP法是1980年T. L. Sauty首次提出的系统分析方法,应用广泛,其步骤如下:①明确目标;②建立层次结构;③构造判断矩阵;④层次单排序及其一致性检验;⑤层次总体排序及其一致性检验。
层次分析法包括总目标层、准则层、指标层等,见表 1。根据上下层之间的关系构造判断矩阵。进行层次单排序一致性检验时,首先计算判断矩阵的最大特征根λmax和一致性指标CI,然后判断CI是否满足一致性要求,当一致性比率CR=CI/RI<0.10时(RI为随机一致性指标),判断矩阵满足一致性。进行层次总排序时也需进行一致性检验,同理,当CR<0.10时,计算结果满足一致性要求。据此运用AHP程序计算各指标的权重分配系数θj (j=1,2,…,m)。
(2)熵权法
熵是系统状态不确定性的一种度量,应用信息熵可以度量各方案中优化目标数据所蕴含的信息量,并依此确定各优化目标的权重。根据信息熵定义,矩阵R中Gj优化目标的信息熵为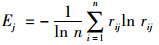 (当rij=0时,rijln rij=0)。指标的差异度为Fj=1-Ej;熵权为
(当rij=0时,rijln rij=0)。指标的差异度为Fj=1-Ej;熵权为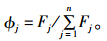
指标熵越小,其熵权越大,表明各方案在该指标上有较大差异。熵权并不代表在轨道交通线网规划评价中指标Gj实际意义上的重要性系数,而是指给定被评价指标集后,在各评价指标值确定的情况下,各指标在竞争意义上的相对激烈程度系数。
(3)组合权重的确定
AHP法综合了专家经验和决策者意向,但其主观性较大。熵权法基于客观数据,但可能会因数据本身的统计误差而造成结果失真,甚至出现得到的权重与实际重要程度不相符的现象。综合分析两种方法的优缺点,本文将AHP法与熵权法的结果相结合,采用式(5)计算指标综合权重:
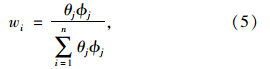
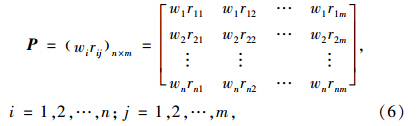
根据TOPSIS思想,可确定加权标准化决策矩阵的正、负理想方案为:

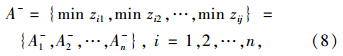
设方案i到理想方案的距离为Li+,到负理想方案的距离为Li-,则:
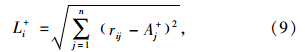
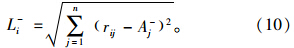
定义方案i到理想方案的贴近度为:

当λi接近0时,方案i越靠近负理想方案,该方案越劣;当λi接近1时,方案i越靠近理想方案,该方案越优。
3 案例分析以西安轨道交通第1版线网规划(6条线)为例,应用本文方法对其进行方案评价。西安市轨道交通线网规划过程中,根据城市布局、功能划分、线网客流测试结果等因素提出了4个备选方案,各方案指标如表 2所示。
| 指标 | 方案1 | 方案2 | 方案3 | 方案4 | 指标 | 方案1 | 方案2 | 方案3 | 方案4 |
|
线路负荷G1/ [万人·(km·d)-1] | 2.98 | 2.9 | 2.83 | 2.99 | 轨道客流占公交客流比例G8 | 0.52 | 0.48 | 0.5 | 0.53 |
| 断面不均匀系数G2 | 1.502 | 1.525 | 1.424 | 1.496 |
节约公交出行时间 G9 /(×104 h·d-1) | 154.6 | 151.7 | 153.7 | 158.5 |
|
客运周转量G3 / [万人·(km·d)-1] | 7 213.48 | 7 081.84 | 7 174.5 | 7 398.11 | 城市土地利用协调程度G10 | 0.8 | 0.75 | 0.7 | 0.8 |
| 换乘系数G4 | 1.38 | 1.39 | 1.41 | 1.34 | 沿线土地开发价值G11 | 0.75 | 0.8 | 0.75 | 0.7 |
| 覆盖中心面积率G5 | 0.73 | 0.57 | 0.73 | 0.71 | 城市景观协调程度G12 | 0.75 | 0.7 | 0.75 | 0.8 |
| 线网规模G6 /km | 249.72 | 248.27 | 261.94 | 151.8 | 工程难易程度G13 | 0.75 | 0.7 | 0.65 | 0.75 |
| 客流集散点衔接数量G7 | 51 | 53 | 53 | 52 | 近期线网可实施性G14 | 0.75 | 0.75 | 0.7 | 0.8 |
Step1 根据表 1确定初始决策矩阵

Step 2 根据式(3)和式(4)得到标准化决策矩阵

Step 3 计算指标权重
采用层次分析法确定权重向量为:
w=0.0800.0430.0740.0520.0810.0530.0760.0860.1050.0880.0660.0560.0700.070。
采用熵权法确定权重向量为:
w=0.0740.0730.0640.0690.0840.0800.0760.0700.0640.0760.0650.0650.0760.065。
根据式(5)确定综合权重为:
w=0.0830.0440.0660.0500.0950.0600.0810.0840.0940.0940.0600.0510.0750.063。
Step 4 根据式(6)得到加权标准决策矩阵

Step 5 根据式(7)和式(8)确定正理想方案和负理想方案
A+={0.0830.0440.0660.0500.0950.0600.0810.0840.0940.0940.0600.0510.0750.063},A-={0,0,0,0,0,0},
Step 6根据式(9)~式(11)计算距离和相对贴近度
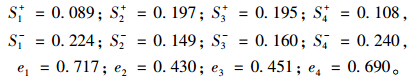
由以上结果得:e1>e4>e3>e2,方案1为最优方案。
4 结论本文提出了基于TOPSIS模型的轨道交通线网方案评价方法,以西安轨道交通线网为例进行了实证研究,取得较好的应用效果,能够为决策者提供客观、合理的决策依据。该方法新颖、科学,值得推广。
(1)在总结分析其他轨道交通线网评价指标和查阅相关文献的基础上,提出了轨道交通线网方案评价指标体系,涵盖了运营效果、网络结构、社会效益、战略发展和可实施性5方面14个指标。
(2)考虑主观和客观两个方面,提出了基于层次分析法和熵权法的指标综合权重确定方法,改善了单一方法造成的结果偏差。
(3)提出了基于TOPSIS模型的轨道交通线网评价方法,该方法基于TOPSIS思想,构造正、负理想方案,通过比较线网方案与正、负理想方案的距离确定了最优方案。
| [1] | 张玉召,严余松,江南,等.基于DEA的城市轨道交通规划线网综合评价研究[J].铁道工程学报,2010(8):96-99. ZHANG Yu-zhao, YAN Yu-song, JIANG Nan, et al. Research on the Comprehensive Evaluation of Urban Rail Transit Network Plan with DEA Method[J]. Journal of Railway Engineering Society, 2010 (8): 96-99. |
| [2] | 温少芳,王明生,刘海宁.投影决策方法在城市轨道交通线网评价中的应用[J]. 铁道运输与经济, 2008,30(1): 64-70. WENG Shao-fang, WANG Ming-sheng, LIU Hai-ning. Application of Projection Method on Evaluation of Urban Rail Transit Network[J]. Railway Transport and Economy, 2008,30(1): 64-70. |
| [3] | 张凯,秦斌斌,刘用渗,等.城市轨道交通线网评价研究[J].铁道工程学报,2014, (3): 97-101. ZHANG Kai,QIN Bin-bin, LIU Yong-shen, et al. Research on the Evaluation of Urban Rail Transit Network[J]. Journal of Railway Engineering Society, 2014(3): 97-101. |
| [4] | 陈旭梅,李凤军,马林涛.城市轨道交通线网方案综合评价指标体系研究[J].城市规划,2001,25(10): 61- 64. CHEN Xu-mei, LI Feng-jun, MA Lin-tao. The Study on the Criterion System for Comprehensive Evaluation of the Urban Rail Network[J]. City Planning Review, 2001, 25(10):61-64. |
| [5] | 纪嘉伦,李福志.城市轨道交通线网规划方案综合评价指标体系研究[J].系统工程理论与实践,2004,24(3):129-133. JI Jia-lun, LI Fu-zhi. A Study on the Synthetic Evaluation Index System of Urban Rail Transit Line Network Planning Scheme[J].Systems Engineering-Theory and Practice, 2004, 24(3): 129-133. |
| [6] | 苏朝霞.城市轨道交通线网规划综合评价的模型和方法[J].物流科技, 2010,33 (6): 143-145. SU Zhao-xia. The Model and Method on Evaluating of the Line-net Planning for Urban Rail Transit[J].Logistics Sci-tech, 2010,33(6): 143-145. |
| [7] | 马超群,王玉萍,陈宽民,等.基于灰色加权关联度的城市轨道线网方案评价[J].长安大学学报: 自然科学版,2007, 27(3): 84-87. MA Chao-qun, WANG Yu-ping, CHEN Kuan-min, et al. Comprehensive Evaluation for Urban Rail Transit Network Based on Grey Weight Relation[J].Journal of Chang'an University: Natural Science Edition, 2007, 27(3): 84-87. |
| [8] | 刘海宁,王明生,温少芳.基于灰色关联度法的轨道交通线网评价[J].石家庄铁道学院学报: 自然科学版, 2007, 20(4): 101-103. LIU Hai-ning, WANG Ming-sheng, WEN Shao-fang. Evaluation of Urban Mass Transit Network Based on Grey Correlation Degree Method[J]. Journal of Shijiazhuang Railway Institute: Natural Science Edition,2007,20(4):101-103. |
| [9] | 李俊芳, 吴小萍. 基于AHP-FUZZY多层次评判的城市轨道交通线网规划方案综合评价[J]. 武汉理工大学学报: 交通科学与工程版, 2007, 31(2): 206-208. LI Jun-fang, WU Xiao-ping. Synthetic Evaluation for Urban Rail Transit Line Network Planning Scheme Based on AHP-fuzzy Method[J]. Journal of Wuhan University of Technology: Transportation Science & Engineering Edition,2007, 31(2): 206-208. |
| [10] | 郝光,牟奇峰,张殿业,等.基于格序偏好的模糊多目标决策方法[J].西南交通大学学报,2006,41(4): 517- 521. HAO Guang, MOU Qi-feng, ZHANG Dian-ye, et al. Approach of Fuzzy Multi-objective Decision-making Based on Lattice-order Preference[J].Journal of Southwest Jiaotong University, 2006,41(4): 517-521. |
| [11] | 刘玉增,钱丙益.轨道交通线网方案比选的多目标格序决策方法[J].交通运输工程学报,2011,11(5): 76-82. LIU Yu-zeng, QIAN Bing-yi. Multi-objective Lattice-order Decision-making Method of Scheme Selection for Rail Transit Network[J]. Journal of Traffic and Transportation Engineering, 2011,11(5): 76-82. |
| [12] | 陈正伟.综合评价技术及应用[M].成都:西南财经大学出版社, 2013. CHEN Zheng-wei. Comprehensive Evaluation Technology and Application[M]. Chengdu: Southwestern University of Finance and Economics Press, 2013. |
| [13] | 于秀慧,李宝山.管理系统工程[M].北京:中国人民大学出版社, 2011. YU Xiu-hui, LI Bao-shan. Management System Engineering[M]. Beijing: China Renmin University Press, 2011. |
| [14] | 郭延永,刘攀,吴瑶.城市轨道交通建设时序确定方法[J].武汉理工大学学报,2013,35(6): 75-80. GUO Yan-yong, LIU Pan, WU Yao. Development of a Method for the Construction Schedule of Urban Rail Transit Lines[J].Journal of Wuhan University of Technology, 2013, 35(6): 75-80. |
 2015, Vol. 31
2015, Vol. 31
