扩展功能
文章信息
- 周康, 何世伟, 宋瑞
- ZHOU Kang, HE Shi-wei, SONG Rui
- 基于出行行为的公交网络多目标优化方法
- Multi-objective Optimization Method of Transit Network Based on Travel Behavior
- 公路交通科技, 2015, Vol. 31 (6): 123-129
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (6): 123-129
- 10.3969/j.issn.1002-0268.2015.06.019
-
文章历史
- 收稿日期:2014-08-18
随着我国城乡一体化的发展和城市化进程的不断推进,城市交通供求矛盾已成为各大中城市面临的首要问题。缓解城市交通压力的根本途径在于大力发展公共交通,合理的公交网络是实现公交系统高效运行的基础。通过合理布设公交线网、科学优化公交网络,能够最大限度地发挥公交系统的效能。
当前公交网络的生成方法主要有两种:一是根据专家经验采用单条线路优化的方法。该方法通常采用逐条布线法、路线优选法(淘汰法)或线路组合优选法等形成基础网络,再对线路调整,以实现整个网络的最优布局。其中以王炜[1]提出的“逐条布线、优化成网”应用最为广泛。由于这种方法主要依赖人工调整,存在较多主观因素,难以实现整体网络的优化。二是对线网进行整体优化。该方法通过建立目标优化模型,借助相关优化软件或智能算法求解模型来实现整个网络最优。林柏梁、杨富社等[2]基于组合优化的角度,提出了优化公交网络设计的非线性0-1规划模型,以所有公交客流的出行时间及要实现公交网络所需的资金投入为目标函数,在满足车站容量限制的条件下,利用模拟退火算法求解目标函数的最小值,以获得公交线路的优化决策。周高卫、罗霞[3]建立了综合公交系统线网布局双层优化模型,上层是0-1数学规划模型,下层是用户平衡分配模型。同时利用改进的IOA算法进行优化求解,克服了传统单式线网优化层次化不显著的缺陷,提高了布局优化过程的求解效率。何胜学、范炳全[4]提出了一种求解公交网络最优路径的标准算法。该算法考虑了公交换乘次数、换乘点选择及出行总成本对求解最优路径的综合影响。通过建立换乘步行时间矩阵,并将过去求解最小换乘次数的换乘矩阵乘法运算变为相应的换乘步行时间矩阵和公交出行时间矩阵的加法运算。
通过分析相关研究发现,目前对公交网络的优化大多数是从出行时间最短、费用最小或换乘次数最少的角度进行研究,很少从居民出行行为的角度综合考虑影响公交网络优化的相关因素来进行整体优化研究。本文在借鉴相关研究的基础上,从居民出行行为角度对现状公交网络进行整体优化。由于影响公交网络优化的因素较多,根据相关因素构建的目标模型通常是多目标模型,相互之间存在冲突,用传统的数学方法难以求得最优解。近年来,随着计算机技术的不断发展,涌现出了大量数学优化软件(其中求解效率较高、应用较广的有LINGO、ILOG Cplex等数学优化软件)以及遗传算法、蚂蚁算法、多智能体算法、粒子群算法、免疫克隆算法等等。通过这些算法及其改进方法可以较好地实现对复杂模型的求解。
1 公交网络描述公交网络是由公交站点以及连接公交站点的公交线路构成,同一公交路段通常会有不同线路的公交出行,同一站点也有不同线路的公交车停靠,区域内的所有公交线路构成了该区域的公交网络。
对于公交乘客而言,根据其出行目的不同,所选择路径也不同。对于同一出行目的地,根据出行时段及路况的不同,所选择的路径也不同。乘客可能会选择换乘最少的线路,也可能选择多次换乘但线路畅通的线路。在公交出行过程中,乘客不仅需要对当前的出行环境做出准确判断,还需要评估出行过程的换乘状况,以达到最优的个人出行目的,如出行费用最小、出行时间最短等。另外,在公交网络内,根据公交站点的分布,乘客出行换乘可分为同站换乘和不同站远距离换乘。
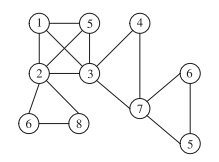
公交网络可以用数学集合表示为G(W,L),其中W为公交网络的各站点集合,i,j∈W;L为公交路段集lij∈L;r∈G为公交网络中的1条线路[5, 6]。在公交网络图中,路段lij是连接站点i和j的边,即lij与点i,j关联,且i和j是相邻的站点。如图 1所示,由4条公交线路构成的公交网络中有节点8个,线路r1由站点1,2,3,5及路段l12,l23,l35组成;线路r2由站点4,3,7及路段l43,l37组成;线路r3由站点6,7,5及路段l67,l75组成;线路r4由站点6,2,8及路段l62,l28组成。其中站点2,3,5,6,7为换乘站点。
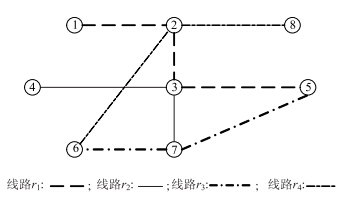
|
| 图 1 公交网络示意图 Fig. 1 Schematic diagram of transit network |
居民在日常出行过程中,通常会以最短路策略选择到达目的地的出行线路。对于交通拥堵不严重的中小城市来说,物理上的最短路通常是最便捷、经济、高效的路线。但对大城市尤其是特大城市来说,由于交通需求大,交通拥堵严重,物理意义上的最短路径往往会由于交通拥堵而增加出行时间及出行成本,成为非最短路径或无法通行的路径。
对于选择小汽车、出租车出行的居民,由于交通方式比较自由、灵活,可以根据出行经验或道路状况,绕过交通拥堵路段,重新选择便捷的出行路径。虽然这样会增加出行距离,但是相对于选择交通拥堵路段能够降低出行时间。然而,城市公交是具有固定行驶线路、固定停靠站点、相对固定运行时刻的交通方式,除非发生重大事件,不能随意更改线路。因此,只能在公交网络优化设计时,分析线路端点之间的土地利用状况,融合绕行策略,绕过交通拥堵点或可能产生交通拥堵的区域,实现公交网络的最优化。
绕行策略是在公交网络优化设计时,尽量使公交线路能绕过拥堵节点,减少拥堵路段公交线路,降低乘客的公交出行时间,提高公交运营的准点率。绕行策略通常会牺牲一部分公交的经济效益来降低乘客的公交出行成本,提高社会效益。
2.2 公交网络约束条件(1)网络密度:《城市道路交通规划设计规范》给出的公交线网密度下限为:
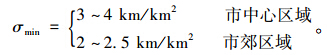
(2)非直线系数:qod≤qmax,qod为公交线路起讫点间的非直线系数;qmax为最大非直线系数(通常取1.5)。
(3)断面客流量:Qodkl< Qmaxkl,Qodkl为断面k,l的客流量;Qmaxkl为断面k,l所允许通过的最大客流量。
(4)断面客流不均匀系数:bodn< bmaxn,bodn为线路断面客流的不均匀系数;bmaxn为线路断面客流的最大不均匀系数(通常取1.5)。
(5)乘客换乘系数:通常情况下,城市居民单程出行换乘次数不超过3次[7],网络的平均换乘系数:

(6)站点服务面积率:根据《城市道路交通规划设计规范》,以服务半径300 m计算,公交站点的覆盖率应大于50%;若以服务半径500 m计算,公交站点的覆盖率应大于90%。
(7)居民出行时耗:T≤Tmax,Tmax为城市中95%左右居民出行单程最大时耗上限。
(8)公交车辆保有量:该项指标一般用万人拥有公交车辆数计,应满足:P/1000≤N≤P/800(大城市),P/1500≤N≤P/1000(中、小城市)。其中,P为城市人口总数;N为折合为标准台数的城市公交车辆数[8]。
2.3 基于出行行为的优化模型公交乘客选择公交出行时要考虑线路的便捷性、经济性等因素,因此公交网络要以乘客出行行为为基础进行合理优化。乘客从起点出发到达目的地,总是希望选择一条便捷而且经济的线路。所谓公交出行的便捷、经济就是出行时间短、换乘少、成本低。随着城市交通拥堵的日益加剧,人们在选择公交出行时更多的希望能绕开拥堵路段,以较长的行驶距离换取更短的出行时间。因此,在对公交网络进行优化时除了要考虑客流量、换乘次数、理论出行时间外,还要考虑由于道路的动态因素造成的拥堵情况而采用必要的绕行优化方法。
(1)线路绕行调整
考虑公交线路中拥堵路段对于出行时间的影响,定义公交线路中拥堵路段为lijd,每条线路中拥堵路段在非拥堵情况下的平均行驶时间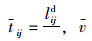 为平均行驶速度。根据相关调查统计分析发现,当拥堵路段超过全部长度的1/3,拥堵时间td≥3t(t为平均行驶时间)时会令乘客产生烦躁情绪,而且会造成较大损失。因此,根据不同区域特征,当路段拥堵时间超过正常通行时间一定值时,可以考虑对该公交线路进行绕行优化,对于没有绕行路线或拥堵路段具有重要节点的情况,对该路段进行固化处理,即连接该节点的公交路段即使出现拥堵也不考虑绕行,而考虑采用交通管制等其他方式优化。
为平均行驶速度。根据相关调查统计分析发现,当拥堵路段超过全部长度的1/3,拥堵时间td≥3t(t为平均行驶时间)时会令乘客产生烦躁情绪,而且会造成较大损失。因此,根据不同区域特征,当路段拥堵时间超过正常通行时间一定值时,可以考虑对该公交线路进行绕行优化,对于没有绕行路线或拥堵路段具有重要节点的情况,对该路段进行固化处理,即连接该节点的公交路段即使出现拥堵也不考虑绕行,而考虑采用交通管制等其他方式优化。
(2)直达客流密度最大
在对公交网络绕行优化的基础上,根据乘客出行的OD,以直达客流密度Dod最大为目标建立优化模型,确定OD对间的合理公交线路集合:
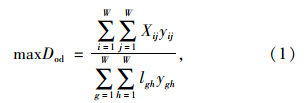


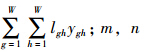 为候选线路的中间站点,该约束是为了控制线路的走向,即同一条线路不应两次或两次以上通过同一个站点;NTR为公交网络客流的不换乘比,NTR=
为候选线路的中间站点,该约束是为了控制线路的走向,即同一条线路不应两次或两次以上通过同一个站点;NTR为公交网络客流的不换乘比,NTR= ,若计算得到的NTR与采用的NTR相差较大,则应以计算的NTR重新进行网络设计,直至采用的不换乘比与计算的不换乘比接近为止[9]。
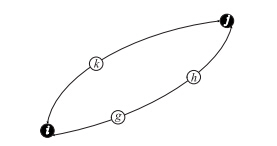
,若计算得到的NTR与采用的NTR相差较大,则应以计算的NTR重新进行网络设计,直至采用的不换乘比与计算的不换乘比接近为止[9]。图 2给出了待优化公交路段,从站点i至j共有2条路径,通过给定的直达客流量Xij以及各路段之间的距离,可以通过模型求得直达客流密度最大路径。
|
| 图 2 站点i,j之间的可选路段 Fig. 2 Optional sections between stop i and stop j |
(3)换乘次数最少
对公交网络的直达客流率进行优化调整后,用space P方法对公交网络进行建模分析,在space P下,公交网络的每条公交线路被看作1个派系,并利用邻接矩阵来表示此无权复杂网络[10]。
通过构建网络邻接矩阵A,可以利用Floyd算法计算得到每两个公交站点间的最小乘车次数矩阵D,这个矩阵即每两个站点间的搜索步数矩阵T。以图 1为例,该示意图在space P方法下的网络结构如图 3所示。
|
| 图 3 Space P描述的公交网络 Fig. 3 Transit network descripted by space P |
通过space P网络结构可以看到每条公交线路上的站点之间不需要换乘,各线路之间的站点可以通过1次或2次换乘完成中转。利用space P方法建模,则可得到公交网络的邻接矩阵A及最小乘车次数矩阵D:


D的值表示的是站点i与站点j之间需要的最少公交乘车次数。同时又表示利用广度优先搜索算法时,从站点i搜索到站点j需要的搜索次数Tij。
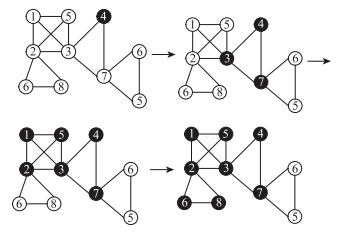
广度优先算法(Breadth-First-Search,BFS),又称宽度(或横向)优先搜索,是一种图形搜索演算法[11]。该算法从根节点开始,沿着树的宽度遍历树的各个节点,如果发现目标,则终止计算。利用广度优先搜索算法对公交网络换乘优化,需要将搜索次数Tij转化为矩阵运算,即对网络的邻接矩阵求幂运算。从节点s依次搜索到它的相邻节点就是原来的邻接矩阵A,二次搜索到它的相邻节点就是对矩阵A求2次幂,即A2=A·A,矩阵A中值为0的节点在A2中变为非0,则表示该节点即为在该次搜索中搜索到的节点。例如Ask=0,A2sk≠0就表示在二次搜索中,从节点s依次搜索,最终搜索到了节点k。同理,三次搜索就是对A求三次幂,即A3=A·A·A,以此类推。利用广度优先搜索算法思想,假设寻找站点4与站点6的最少次数换乘方案,即从节点4搜索到节点6,搜索过程如图 4所示。
|
| 图 4 公交网络的广度优先搜索过程 Fig. 4 Search process of transit network by Breadth-First-Search |
通过以上搜索过程就可以搜索到站点4到站点6的最少换乘路径为4→3→2→6,并且搜索到中间换乘站点为3和2。若具有相同换乘次数的换乘线路有多条,即可以选择同样换乘次数的换乘点有多个,可以一一记录下所有可行的搜索路径,可得到所有换乘次数相同(均为最少换乘次数)的不同换乘方案,再以出行时间最小为目标进行优化[12]。
(4)出行时间最短
在给定的公交网络中,同一OD对间存在多种路线组合模式,各公交站点i,j间所有公交出行者的出行时间加总得到决策变量T。在上述优化的基础上以OD客流出行时间(候车时间、乘车时间、换乘时间)T最小为目标,构建公交网络优化目标模型:
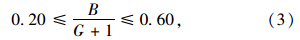

基于上述优化模型,选择合适的求解方法。分析模型特点不难发现,上述模型均为线性模型,对于数据量较少的小规模公交网络来说,计算量较小,很容易得到结果;当公交网络规模较大,结构复杂时,就会产生大量数据,求解会比较困难。根据模型特征,选择ILOG Cplex数学优化软件进行求解优化。该软件能够在占用较少内存的基础上,快速求解大规模、复杂的模型。在数学优化领域具有较高的地位。综合以上4阶段的公交网络优化方法,利用C#编程并调用ILOG对模型进行求解分析。
4 算例分析和评价对图 5所示区域内的公交网络进行优化,其初始公交网络见表 1。已知各节点为确定的站点,各节点之间的连接线为该区域可通行的公交道路,路段上的数字为站点间距,A~K为该区域的交通小区,OD矩阵如表 2所示。由于篇幅所限,网络邻接矩阵A以及每两个公交站点间的最小乘车次数矩阵D等数据不再一一给出,具体优化过程如下:

|
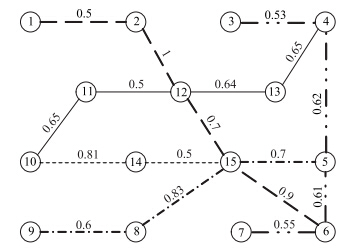
| 注:图中的连线为公交网络,不同的连线代表不同的线路和路段,拥堵路段分别为:2-3,3-12,7-8,9-14,5-15,10-11,8-15。 图 5 初始公交网络(单位:km) Fig. 5 Initial transit network (unit: km) |
| 序号 | 公交线路 | 序号 | 公交线路 |
| 1 | 1-2-3-12-15-6 | 4 | 1-10-9-14 |
| 2 | 3-4-5-6-7 | 5 | 5-6-7-8-9 |
| 3 | 1-11-12-13 | 6 | 10-14-15-5-13-4 |
| 小区 | A | B | C | D | E | F | G | H | I | J | K |
| A | 0 | 50 | 90 | 150 | 210 | 270 | 230 | 190 | 120 | 60 | 70 |
| B | 50 | 0 | 45 | 70 | 96 | 153 | 238 | 359 | 320 | 261 | 122 |
| C | 83 | 43 | 0 | 34 | 76 | 107 | 141 | 201 | 252 | 281 | 171 |
| D | 121 | 82 | 50 | 0 | 62 | 103 | 154 | 210 | 282 | 311 | 205 |
| E | 201 | 154 | 115 | 56 | 0 | 67 | 103 | 144 | 190 | 142 | 151 |
| F | 231 | 192 | 157 | 102 | 60 | 0 | 52 | 101 | 147 | 192 | 145 |
| G | 291 | 243 | 191 | 130 | 96 | 58 | 0 | 64 | 117 | 158 | 216 |
| H | 150 | 214 | 271 | 254 | 218 | 163 | 78 | 0 | 63 | 114 | 152 |
| I | 93 | 144 | 202 | 241 | 190 | 155 | 91 | 52 | 0 | 55 | 96 |
| J | 57 | 93 | 152 | 217 | 163 | 212 | 173 | 114 | 60 | 0 | 57 |
| K | 81 | 90 | 101 | 161 | 102 | 171 | 203 | 191 | 90 | 53 | 0 |
(1)首先利用EMME软件对该区域划分的各小区公交出行OD进行流量分配,得到初始的公交网络布局。
(2)根据各公交线路上拥堵路段的拥堵时长确定绕行优化。
(3)利用ILOG Cplexs数学优化软件结合EMME分配的公交OD对直达客流密度模型进行求解,根据直达客流最大结合公交网络约束条件确定优化后的公交网络。
(3)利用space P方法及广度优先算法对公交网络进行最小换乘优化。
(4)对同一OD间的所有公交线路进行出行时间计算,在满足约束条件的前提下实现公交网络布局的最优。
为了简化求解过程,假设该区域公交网络内换乘节点的平均换乘时间为5 min,乘客从出发点到起始公交站点的时间忽略不计,公交平均行驶速度为25 km/h,站点4,15属于重要站点,经过该站点的公交线路不能绕过该站点,因此对其固化处理。
优化后的公交网络见表 3和图 6。
| 序号 | 公交线路 | 序号 | 公交线路 |
| 1 | 1-2-12-15-6 | 4 | 10-14-15 |
| 2 | 10-11-12-13-4 | 5 | 7-6-5-4-3 |
| 3 | 9-8-15-5 |
|
| 注:图中的连线为公交网络,不同的连线代表不同的线路 图 6 主从接触面 Fig. 6 Master-slave contact surface |
从公交网络优化的算例可以发现,通过4阶段的逐步推进,在优化公交网络的同时能够很好地避免对次优线路的删除。由于加入了绕行策略优化方法,在实现最优线路搜索的同时能对通行较差的公交线路进行绕行优化,从而有效保证了区域公交网络的密度。通过对重点公交站点的固化,保证了公交站点的均匀分布。
5 结论(1)通过公交网络的数学描述,构建了公交网络的数学表达式。在分析公交乘客出行特征的基础上,提出了公交网络的4阶段优化方法。
(2)根据公交需求OD,利用EMME进行初始公交网络布设,在初始公交网络基础上依次进行绕行优化、直达客流率最大优化、换乘次数最小优化及出行时间最小优化,最终得到优化网络。
(3)绕行优化是在比较拥堵路段拥堵时间与正常通行时间的基础上做出决策的,对于没有绕行线路或具有重要意义站点的拥堵路段进行固化处理。
(4)在绕行优化的基础上,对公交网络进行直达客流率最大优化。
(5)利用space P方法对公交网络进行派系划分,构造邻接矩阵,然后利用广度优先算法进行换乘最少优化。
(6)构建出行时间最短模型,对同一OD对间的公交线路进行优化。
(7)通过算例验证了该方法的可行性及优越性。
(8)该方法针对小规模公交网络具有较高的优化效率,但是对于复杂的公交网络需要在求解方法上做进一步的改进、优化。
| [1] | 王炜,杨新苗,陈学武.城市公共交通系统规划方法与管理技术[M].北京:科学出版社,2002. WANG Wei,YANG Xin-miao,CHEN Xue-wu. Urban Public Transport System Planning Methods and Management Techniques [M]. Beijing: Science Press,2002. |
| [2] | 林柏梁,杨富社,李鹏.基于出行费用最小化的公交网络优化模型[J].中国公路学报,1999,12(1):79-83. LIN Bo-liang,YANG Fu-she,LI Peng. Designing Optimal Bus Network for Minimizing Trip Times of Passenger Flows[J]. China Journal of Highway and Transport,1999,12(1):79-83. |
| [3] | 周高卫,罗霞.多式综合公交系统线网布局优化模型及仿真[J].计算机应用研究,2013,30(4):1035-1040. ZHOU Gao-wei,LUO Xia. Network Layout Optimization Model of Multi-modal Comprehensive Public Transit System and Simulation[J]. Application Research of Computers,2013,30(4):1035-1040. |
| [4] | 何胜学,范炳全.公交网络最优路径求解算法[J]. 交通运输工程与信息学报,2007,5(1):22-27. HE Sheng-xue,FAN Bing-quan. Optimal Path Searching Algorithm in Transit Network[J]. Journal of Transportation Engineering and Information,2007,5(1):22-27. |
| [5] | 汪涛,许乐,张继,等.城市公交网络的拓扑结构及其演化模型研究[J].公路交通科技,2009,26(11):108-112. WANG Tao,XU Le,ZHANG Ji,et al. Research on Topological Structure and Evolution Model of Urban Transit Network [J]. Journal of Highway and Transportation Research and Development,2009,26(11):108-112. |
| [6] | 黄敏.多层次公交线网拓扑结构分析[J].公路交通科技,2010,27(5):93-99. HUANG Min. Analysis on Topology Frame of Multi-level Transit System Network[J]. Journal of Highway and Transportation Research and Development,2010,27(5):93-99. |
| [7] | 许伦辉,林泉.基于GBAS的公交出行最优路径选择算法[J].公路交通科技,2010,27(3):154-158. XU Lun-hui,LIN Quan. Transit Trip Optimal Route Choice Algorithm Based on GBAS[J]. Journal of Highway and Transportation Research and Development,2010,27(3):154-158. |
| [8] | 周康,马晓旦,夏晓梅.基于最小换乘的公交线网优化模型[J].城市公共交通,2011 (6):43-45. ZHOU Kang,MA Xiao-dan,XIA Xiao-mei. Model of Public Transportation Network Optimization Based on Minimal Transfer [J]. Urban Public Transport,2011 (6):43-45. |
| [9] | 于滨, 杨永志,杨忠振,等.基于直达客流密度最大的公交线网优化[J].哈尔滨工业大学学报,2009,41(2):205-207. YU Bin,YANG Yong-zhi,YANG Zhong-zhen,et al. Transit Network Optimization Based on Direct Passenger Flow Density Maximization[J]. Journal of Harbin Institute of Technology,2009,41(2):205-207. |
| [10] | YANG Xu-hua,WANG Bo,WANG Wan-liang,et al. Research on Some Bus Transport Networks with Random Overlapping Clique Structure [J].Communications in Theoretical Physics,2008,49(11):1249-1254. |
| [11] | 汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].北京:清华大学出版社,2006. WANG Xiao-fan,LI Xiang,CHEN Guan-rong. Complex Network Theory and Its Application [M].Beijing: Tsinghua University Press,2006. |
| [12] | 王波.基于派系的复杂网络及其在公交网络上的应用研究[D].杭州:浙江工业大学,2009:64-72. WANG Bo. Study on Complex Network Based on Cliques and Its Application in Bus Transport Network [D]. Hangzhou: Zhejiang University of Technology,2009:64-72. |
 2015, Vol. 31
2015, Vol. 31
