扩展功能
文章信息
- 胡腾飞, 华旭刚, 温青, 陈政清
- HU Teng-fei, HUA Xu-gang, WEN Qing, CHEN Zheng-qing
- 中央扣对大跨悬索桥模态特性的影响
- Influence of Central Buckles on Modal Characteristics of Long-span Suspension Bridge
- 公路交通科技, 2015, Vol. 31 (6): 89-94
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (6): 89-94
- 10.3969/j.issn.1002-0268.2015.06.014
-
文章历史
- 收稿日期:2014-11-18
2. 广西交通科学研究院, 广西 南宁 530007
2. Guangxi Research Institute of Communications Science, Nanning Guangxi 530007, China
自1940年美国的旧Tacoma桥发生风毁事故以来,改善悬索桥动力特性的措施一直是桥梁界重视的问题,而在桥梁跨中设置中央扣是一种有效措施[1, 2, 3, 4]。1950年中央扣在原地重建的新Tacoma桥上得到应用以来[1],主要发展为刚性中央扣和柔性中央扣。从中央扣的应用情况来看,欧美国家偏向于采用刚性中央扣,日本偏向于采用柔性中央扣。
近些年来,中央扣已经应用于国内的许多悬索桥[2, 3],但相关文献并不多见。目前,在中央扣对桥梁抗风性能影响研究方面,王浩等[4, 5, 6]以首次采用刚性中央扣的润扬大桥为背景,得出刚性中央扣的不同精度模拟对该桥动力特性的影响很小、中央扣对大跨度悬索桥抖振响应的影响与风速有关等结论。徐勋[7, 8]以四渡河大桥为背景,得出中央扣能够提高结构反对称抗扭刚度和限制结构纵飘特性等结论。随后,邹科官等[9, 10]也采用有限元法得到了与上述类似的结论。而在中央扣对桥梁自振特性影响研究方面,彭旺虎[
11-12]阐述了中央扣提高悬索桥反对称扭转频率的机理,并对有、无中央扣悬索桥的纵向和竖向耦合振动特性进行了理论研究。曹永睿[13, 14]则对柔性中央扣的锚固方式及受力性能进行了分析和比较。然而,在中央扣对悬索桥动力特性影响研究方面,以上许多结论均来自于有限元计算或理论分析,缺乏必要的实测资料或试验数据。
本文以矮寨大桥为背景,采用ANSYS分析和比较了无中央扣、跨中设置1对和3对斜索的柔性中央扣以及刚性中央扣4种计算工况的模态特性及其变化规律,并进一步制作了该桥的全桥气弹模型,测试了模型相应工况下的模态特性,并与有限元结果进行了对比。相关研究结果可为该桥的风洞试验提供有用信息,并为今后中央扣在此类桥梁中的应用提供参考。
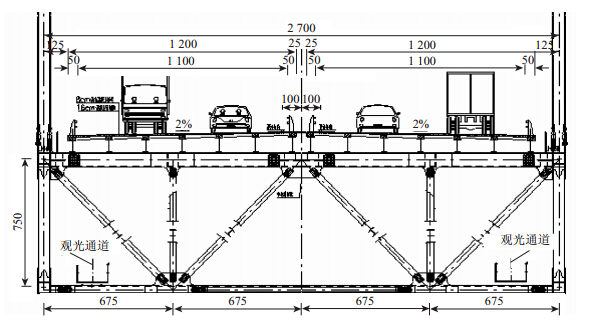
1 工程背景矮寨大桥是吉茶高速公路的控制性工程,峡谷两侧山体不等高,跨中桥面设计标高距谷底高度340 m,是世界上跨峡谷跨径最大的钢桁加劲梁悬索桥。该桥全长1 176 m,主缆矢跨比1∶9.6,两主缆形心距27 m;加劲梁全长1 000.5 m,中跨主缆两端靠桥塔处各有无索区长度为:吉首岸95 m,茶洞岸109.5 m;加劲梁采用钢桁梁方案,梁高7.5 m,桁架节间距7.25 m;桥面行车道系采用钢纵梁与混凝土桥面板的结合方式,钢纵梁与主桁上横梁之间采用橡胶支座支承,左右幅桥面行车道采用有间距分离布置,每幅桥面宽度12 m,桥面系设置双向2%横坡。图 1为该桥建成后的实况图,主桁及桥面横断面布置如图 2所示。

|
| 图 1 矮寨大桥实况图 Fig. 1 Photo of Aizhai bridge |
|
| 图 2 主梁标准横断面图(单位:cm) Fig. 2 Standard section of main girder (unit: cm) |
在矮寨大桥悬索桥有限元分析中,主桁结构和桥塔采用空间梁单元BEAM188进行离散,吊杆与主缆使用空间杆单元LINK10进行离散,由于桥面系与主桁结构分离,不参与整体受力,因此桥面系采用MASS21单元模拟其平动质量与扭转质量。矮寨大桥有限元模型如图 3所示。

|
| 图 3 全桥空间有限元模型 Fig. 3 Finite element model of bridge |
为方便研究中央扣对悬索桥模态特性的影响,按中央扣刚度增加的顺序定义了如表 1所示的4种有限元模型计算工况。通过比较M-B与M-C,可知设置几对斜索较好;对比M-A与M-C可以了解中央扣的作用,对比M-C和M-D可以比较刚性中央扣与柔性中央扣对悬索桥动力特性影响的差异。
| 模型 | 中央扣类型 | 中央扣模拟方式 |
| M-A | 跨中短吊索 | 无 |
| M-B | 柔性中央扣 | 1对斜索(LINK10) |
| M-C | 3对斜索(LINK10) | |
| M-D | 刚性中央扣 | 1对刚臂(BEAM4) |
在动力特性有限元分析中,首先考虑主缆的初始应变、结构自重以及几何非线性对该桥进行静力分析,然后在静力分析的基础上,得到结构的初应力刚度矩阵后再进行特征值与特征向量求解,最后得出结构的自振频率与按质量规一化的振型。4种计算工况的主要模态频率和振型特征如表 2所示。
| 振型特征 | fM-A/Hz | fM-B/Hz | fM-C/Hz | fM-D/Hz | fM-B /fM-A | fM-C /fM-A | fM-D /fM-A | |
| 一阶侧弯 | 正对称 | 0.056 0(1) | 0.056 1(1) | 0.056 1(1) | 0.057 1(1) | 1.002 | 1.002 | 1.018 |
| 反对称 | 0.133 9(4) | 0.137 2(3) | 0.140 2(3) | 0.143 1(3) | 1.025 | 1.047 | 1.069 | |
| 一阶竖弯 | 正对称 | 0.160 6(5) | 0.160 6(4) | 0.160 6(4) | 0.160 7(4) | 1.000 | 1.000 | 1.001 |
| 0.214 4(6) | 0.214 1(5) | 0.214 2(5) | 0.214 3(5) | 0.999 | 0.999 | 0.995 | ||
| 反对称 | 0.257 6(9) | 0.253 2(8) | 0.254 4(8) | 0.254 8(7) | 0.983 | 0.988 | 0.989 | |
| 一阶扭转 | 正对称 | 0.294 6(13) | 0.294 6(13) | 0.294 7(12) | 0.301 2(12) | 1.000 | 1.000 | 1.022 |
| 反对称 | 0.323 7(14) | 0.333 4(14) | 0.343 7(14) | 0.353 6(14) | 1.032 | 1.062 | 1.092 | |
|
主缆侧向 交叉摆动 | 正对称 | 0.233 2(7) | 0.234 0(6) | 0.235 5(6) | 0.256 9(8) | 1.003 | 1.010 | 1.102 |
| 反对称 | 0.257 8(10) | 0.257 8(9) | 0.257 8(9) | 0.257 8(9) | 1.000 | 1.000 | 1.000 | |
|
主缆整体 平行摆动 | 正对称 | 0.396 4(17) | 0.398 5(17) | 0.402 5(16) | 0.425 8(16) | 1.005 | 1.015 | 1.074 |
| 反对称 | 0.262 5(11) | 0.262 5(10) | 0.262 6(10) | 0.262 6(10) | 1.000 | 1.000 | 1.000 | |
|
竖弯伴随 纵飘 | 一阶 | 0.095 1(2) | 0.116 0(2) | 0.116 4(2) | 0.116 5(2) | 1.220 | 1.224 | 1.225 |
| 二阶 | 0.129 1(3) | 0.293 8(12) | 0.375 2(15) | 0.444 2(17) | 2.276 | 2.906 | 3.424 | |
| 注:括号内数字表示该振型在对应模型中出现的模态阶次 | ||||||||
通过对矮寨大桥跨中设置4种联结模式下自振频率与振型特征的分析和比较,可以得出以下结论。
(1)该桥基频为0.056 1 Hz,基本周期较长,其对应振型为一阶对称侧弯振型;第二阶模态频率为0.116 4 Hz,相应振型为一阶反对称竖弯伴随纵飘振型,这些均符合大跨度悬索桥柔性结构的一般规律[7, 8]。
(2)相比1对斜索的柔性中央扣模型,采用3对斜索模型的模态频率略高。
(3)4种模型的第二阶模态振型均为一阶的纵飘伴随竖弯振型,相比跨中短吊索模型,有中央扣模型的纵飘频率平均要高出22.3%。此外,跨中短吊索模型紧接着在第三阶模态出现纵飘伴随竖弯振型,而有中央扣模型则明显推迟,这些均与中央扣的类型无关。由此可见,中央扣能够大幅提高悬索桥的纵飘刚度。究其原因,中央扣为斜向受拉构件,能够将加劲梁所受的纵向力传递给主缆,相当于通过主缆对加劲梁施加了纵向约束,增强了该桥的纵向刚度,进而提高了纵飘振型的模态频率。
(4)对于侧弯与竖弯模态,中央扣对反对称模态频率的影响比正对称大。一阶反对称侧弯的模态频率随中央扣刚度的增大而有所增加,中央扣对竖弯模态频率影响较小。
(5)中央扣对正对称扭转振型的模态频率影响很小,而反对称扭转振型的模态频率随中央扣刚度的增大而增加,相比M-A,有中央扣的M-B,M-C,M-D模态频率分别提升了3.2%,6.2%和9.2%。究其原因,悬索桥在反对称扭转振动时,主缆在中央扣前、后会形成反对称的附加缆力,使得主缆获得额外的弹性应变能,主梁的自振频率得到提高。
跨中没有设置中央扣时,该桥的一阶反对称竖弯频率为0.129 1 Hz,一阶反对称扭转频率为0.323 7 Hz,相应的扭弯频率比为2.51;设置3对斜索的柔性中央扣以后,相应的竖弯频率和扭转频率分别为0.116 4 Hz和0.343 7 Hz,扭弯频率比为2.95。就桥梁抗风而言,中央扣最大的作用是能够较大幅度提高结构的反对称扭转频率(对于无中央扣的一般悬索桥体系通常为其扭转基频,相应的模态组合参数将为桥梁风洞试验设计提供重要参考),使桥梁反对称模态组合下的扭弯频率比增加,进而增强该桥的抗风稳定性。
(6)中央扣对主缆振动的影响与对主梁侧弯和扭转振型的影响刚好相反。中央扣对主缆的反对称振动影响很小,而在中央扣对主缆正对称模态频率的影响方面,柔性中央扣对缆索振动几乎没有影响,但设置刚性中央扣以后,该桥主缆正对称侧向交叉摆动和整体平行摆动的模态频率分别提高了7.4%和10.2%,这也是刚性中央扣与柔性中央扣对悬索桥模态特性的影响差异最大所在。
(7)相比跨中设置短吊索,中央扣使得悬索桥的整体刚度有所增加,相应各阶频率也得到增加。
4 全桥气弹模型动力测试 4.1 全桥气弹模型设计与制作全桥气弹模型的设计,不仅满足相似性条件,还应当严格满足在实桥与全桥气弹模型之间保持弹性参数及惯性(质量)参数等6种参数的一致性[15],才能保证模型的结构动力特性与实桥相似。矮寨大桥跨度较大,为尽可能地增大模型比例,考虑到矮寨大桥两边跨主梁对大桥加劲梁的抗风稳定性影响较小,且圆形截面的主缆通常不会产生自激力,因此,在全桥气弹模型制作中两边跨主缆可不进行模拟,其对结构的刚度贡献可通过等效的方法在气弹模型中加以考虑[16]。同时,为了满足湖南大学风工程试验中心边界层风洞试验段尺寸要求,并考虑到模拟主缆的钢丝直径规格系列而采用1∶245缩尺比进行全桥气弹模型的制作与加工,对应实桥与模型的频率比为1∶15.65。全桥气弹模型如图 4所示。

|
| 图 4 矮寨大桥气弹模型 Fig. 4 Aeroelastic model of Aizhai bridge |
为了保证制作加工的气弹模型能真实地反映实桥的动力特性,需要保证制作的气弹模型在动力特性上达到模型理想设计的误差范围(±5%)内。下文用“C-X”表示与有限元分析结果相对应的试验工况(如C-A表示与有限元中M-A相对应的试验工况)。根据悬索桥的振型特点,测量侧弯模态时加速度传感器固定在加劲梁侧向,测量竖弯和扭转模态时加速度传感器竖向固定在桥面板上。根据不同模态的特点采取不同的人工激振方式可激发出上述一阶模态。试验中,测试采用3对斜索的中央扣模型(矮寨大桥实际采用方案),并对其动力特性进行检验。试验结果如表 3所示,C-C中央扣结构模拟如图 5所示。由表 3可知,模型的各阶模态频率实测值与目标值吻合较好,动力特性均满足要求。
| 振型 |
实桥 频率/Hz |
模型目标 频率/Hz |
模型实测 值/Hz | 误差/% |
| 纵飘 | 0.116 4 | 1.822 | 1.855 | 1.78 |
| 一阶正对称侧弯 | 0.056 1 | 0.878 | 0.879 | 0.11 |
| 一阶反对称竖弯 | 0.116 4 | 1.822 | 1.855 | 1.78 |
| 一阶反对称侧弯 | 0.140 2 | 2.194 | 2.246 | 2.32 |
| 一阶正对称竖弯 | 0.160 6 | 2.513 | 2.539 | 1.02 |
| 一阶正对称扭转 | 0.294 7 | 4.612 | 4.590 | -0.48 |
| 一阶反对称扭转 | 0.343 7 | 5.379 | 5.556 | 3.3 |

|
| 图 5 中央扣结构模型(C-C) Fig. 5 Structure model of central buckles(C-C)e |
得到C-C模态频率后,再依次剪断相应中央扣得到其他工况下的模态频率,试验结果如表 4所示。
| 振型特征 |
FC-A/ Hz |
FC-B/ Hz |
FC-C/ Hz |
FC-B/ fC-A |
FC-C/ fC-A | |
| 纵飘 | 反对称 | 1.592 | 1.841 | 1.855 | 1.158 | 1.165 |
| 一阶侧弯 | 正对称 | 0.879 | 0.880 | 0.879 | 1.001 | 1.000 |
| 反对称 | 2.131 | 2.192 | 2.246 | 1.029 | 1.054 | |
| 一阶竖弯 | 正对称 | 2.509 | 2.538 | 2.539 | 1.012 | 1.012 |
| 反对称 | 1.834 | 1.841 | 1.855 | 1.004 | 1.011 | |
| 一阶扭转 | 正对称 | 4.590 | 4.590 | 4.590 | 1.000 | 1.000 |
| 反对称 | 5.157 | 5.493 | 5.556 | 1.065 | 1.077 | |
由表 4可知,中央扣对一阶正对称侧弯和一阶正对称扭转模态频率的影响很小,一阶反对称侧弯频率随中央扣刚度的增加略有增加,这与有限元分析的结果基本一致。中央扣对一阶竖弯模态频率影响很小,试验结果与有限元分析结果比较吻合。对于一阶反对称扭转模态,由于采用模拟中央扣的钢丝直径(实际直径d=0.2 mm)达不到模型设计所需的尺寸(理论直径d=0.014 mm),模拟斜索的钢丝实际刚度介于柔性中央扣与刚性中央扣之间,使得数据略微偏大,导致试验结果介于有限元模型中分别采用柔性中央扣与刚性中央扣的分析值之间(3.2%~9.2%),这也反映出一阶反对称扭转的模态频率随中央扣刚度的增大而增加。此外,相比跨中设置短吊索模型,中央扣也使得悬索桥的整体刚度有所增加,相应各阶频率也有不同程度的增加。
需要指出的是,桥梁抗风研究中主要考虑了主梁的侧向、竖向和扭转振动,而放松了对纵飘振动的要求。试验中无中央扣试验模型的纵飘频率误差为7%,这是由于模型在实际制作中,加劲梁在桥塔位置处的纵向滑动很难完全模拟,即存在一定的摩擦,其对纵向自由度的影响介于完全自由与纵向约束之间,因此导致纵飘频率测试结果偏大。而中央扣对纵飘频率的提升约为16%,与理论分析结果(22%)存在一定差异,但仍从整体上反应了中央扣能够大幅度地提高主梁的纵飘频率。
5 结论本文以矮寨大桥为背景,采用ANSYS分析了中央扣对大跨度悬索桥模态特性的影响,对比了刚性中央扣和柔性中央扣对大跨悬索桥模态特性影响的差异,并通过该桥全桥气弹模型动力特性试验对有限元分析结果进行了验证。通过本文的研究,可以得出以下几点结论。
(1)中央扣对反对称侧弯模态频率的影响比正对称大,对竖弯模态频率的影响较小;中央扣能够大幅提高悬索桥的纵飘频率。
(2)中央扣最大的作用是能够较大幅度地提高结构的反对称扭转频率,使得反对称模态组合下的扭弯频率比增加,有利于桥梁抗风。
(3)相比跨中设置短吊索,中央扣使得悬索桥的整体刚度增加,相应各阶频率也得到增加。相比跨中设置1对斜索的柔性中央扣模型,采用3对斜索模型的模态频率略高。
(4)刚性中央扣与柔性中央扣对悬索桥动力特性影响的最大差别,在于柔性中央扣对缆索振动几乎没有影响,但设置刚性中央扣以后,该桥主缆正对称振动的频率均有很大提高。
| [1] | VIOLA J M,SYED S,CLENANCEl J. The New Tacoma Narrows Suspension Bridge:Construction Support and Engineering[C]// Proceedings of the 2005 Structures Congress and the 2005 Forensic Engineering Symposium. New York:Structure Engineering Institute of the America Society of Civil Engineers,2005:1-12. |
| [2] | 单宏伟,韩大章,吕立人. 润杨长江公路大桥悬索桥中央扣设计[J]. 公路,2004(8):58-61. SHAN Hong-wei,HAN Da-zhang,LV Li-ren. Design of Center Nodes of Runyang Suspension Bridge Over Yangtze River[J]. Highway,2004(8):58-61. |
| [3] | 高剑,刘高,曾宇. 贵州坝陵河钢桁架悬索桥中央扣设计[C]//中国公路学会桥梁和结构工程分会2007年全国桥梁学术会议论文集. 北京:人民交通出版社,2007:101-106. GAO Jian,LIU Gao,ZENG Yu. Design of Central Buckles of Guizhou Baling River Steel Trussed Suspension Bridge[C]//Proceedings of 2007 National Conference on Bridge Engineering,Bridge and Structural Engineering Branch of CHTS. Beijing:China Communications Press,2007:101-106. |
| [4] | 王浩,李爱群,杨玉冬,等. 中央扣对大跨度悬索桥动力特性的影响[J]. 中国公路学报,2006,19(6):49-53. WANG Hao,LI Ai-qun,YANG Yu-dong,et al. Influence of Central Buckle on Dynamic Behavior of Long-span Suspension Bridge [J]. China Journal of Highway and Transport,2006,19(6):49-53. |
| [5] | 王浩,李爱群. 中央扣对大跨度悬索桥风致抖振响应的影响[J]. 土木工程学报,2009,42(7):78-84. WANG Hao,LI Ai-qun. Influence of Central Buckle on Wind-induced Buffeting Response of Long-span Suspension Bridges[J]. China Civil Engineering Journal,2009,42(7):78-84. |
| [6] | 李枝军,李爱群,韩晓林. 润扬大桥悬索桥动力特性分析与实测变异性研究[J]. 土木工程学报,2010,43(4):92-98. LI Zhi-jun,LI Ai-qun,HAN Xiao-lin. Dynamic Analysis and Experimental Study of Variation of the Dynamic Parameters of the Runyang Suspension Bridge[J]. China Civil Engineering Journal,2010,43(4):92-98. |
| [7] | 徐勋,强士中,贺拴海. 中央扣对大跨悬索桥动力特性和汽车车列激励响应的影响[J]. 中国公路学报,2008,21(6):57-63. XU Xun,QIANG Shi-zhong,HE Shuan-hai. Influence of Central Buckle on Dynamic Behavior and Response of Long-span Suspension Bridge under Vehicle Group Excitation[J]. China Journal of Highway and Transport,2008,21(6):57-63. |
| [8] | 徐勋,强士中. 中央扣对大跨悬索桥动力特性和地震响应的影响研究[J]. 铁道学报,2010,32(4):84-91. XU Xun,QIANG Shi-zhong. Influence of Central Buckle on Dynamic Behavior and Seismic Response of Long-span Suspension Bridge[J]. Journal of China Railway Society,2010,32(4):84-91. |
| [9] | 皱科官,王浩,梁书亭. 中央扣对三塔悬索桥动力特性的影响[J]. 建筑科学与工程学报,2009,26(4):49-53. ZOU Ke-guan,WANG Hao,LIANG Shu-ting. Influences of Central Buckles on Dynamic Behaviors of Triple-tower Suspension Bridge[J]. Journal of Architecture and Civil Engineering,2009,26(4):49-53. |
| [10] | 王军,金红亮. 柔性中央扣对大跨悬索桥动力特性的影响[J]. 上海公路,2010(4):35-38,13. WANG Jun,JIN Hong-liang. Influence of Flexible Central Buckle on Dynamic Behavior of Long-span Suspension Bridge[J]. Shanghai Highways,2010(4):35-38,13. |
| [11] | 彭旺虎,邵旭东.设置中央扣悬索桥的扭转自振分析[J]. 中国公路学报,2013,26(5):76-87. PENG Wang-hu,SHAO Xu-dong. Analysis of Free Torsional Vibration of Suspension Bridges with Center Ties[J]. China Journal of Highway and Transport,2013,26(5):76-87. |
| [12] | 彭旺虎,邵旭东. 悬索桥纵向和竖向耦合自振研究[J]. 工程力学,2012,29(2):142-148. PENG Wang-hu,SHAO Xu-dong. Study on Longitudinal and Vertical Coupling Vibration of Suspension Bridges[J]. Engineering Mechanics,2012,29(2):142-148. |
| [13] | 曹永睿,韩立中,姜锡东,等. 钢桁梁悬索桥柔性中央扣梁端锚固方式比较研究[J]. 公路交通科技,2013,30(9):80-86. CAO Yong-rui,HAN Li-zhong,JIANG Xi-dong,et al. Comparative Study of Cable-girder Anchorage Styles for Flexible Central Buckles of Steel Truss Girder Suspension Bridge [J]. Journal of Highway and Transportation Research and Development,2013,30(9):80-86. |
| [14] | 曹永睿,柴增铧. 悬索桥柔性中央扣锚固系统受力分析[J]. 铁道建筑,2013(8):35-37. CAO Yong-rui,CHAI Zeng-hua. Analysis of Forces Exerted on Flexible Central Buckle Anchorage System of Suspension Bridge[J]. Railway Engineering,2013(8):35-37. |
| [15] | 许福友,马如进,陈艾荣,等. 苏通大桥全桥气弹模型设计与模态调试[J]. 工程力学,2009,26(12):150-154,174. XU Fu-you,MA Ru-jin,CHEN Ai-rong,et al. Full Aeroelastic Model Design and Modal Test for Sutong Bridge[J]. Engineering Mechanics,2009,26(12):150-154,174. |
| [16] | 李春光,陈政清,张志田. 大跨度桁式加劲梁悬索桥气弹模型等效设计[J]. 振动与冲击,2009,28(9):171-174,187,222. LI Chun-guang,CHEN Zheng-qing,ZHANG Zhi-tian. Equivalent Design of Aeroelastic Model for a Long-span Suspension Bridge with Truss Stiffening Girder[J]. Journal of Vibration and Shock,2009,28(9):171-174,187,222. |
 2015, Vol. 31
2015, Vol. 31
