扩展功能
文章信息
- 杨斌, 安关峰, 单成林
- YANG Bin, AN Guan-feng, SHAN Cheng-lin
- 增大截面加固受弯构件的正截面承载力计算方法
- Calculation Method of Bearing Capacity on Cross-section of Bending Member Strengthened with Enlarged Section
- 公路交通科技, 2015, Vol. 31 (6): 81-88
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (6): 81-88
- 10.3969/j.issn.1002-0268.2015.06.013
-
文章历史
- 收稿日期:2014-08-15
2. 华南理工大学, 广东 广州 510640
2. South China University of Technology, Guangzhou Guangdong 510640, China
按现行规范,在进行增大截面法加固钢筋混凝土受弯构件的正截面抗弯承载力计算时,房屋建筑工程采用《混凝土结构加固设计规范》(GB 50367—2013)(以下简称《GB加固规范》),桥梁工程采用《公路桥梁加固设计规范》(JTG/T J22—2008)(以下简称《JTG加固规范》),这两本规范的设计计算方法不同。另外,在近几年,有关桥梁工程专家教授对《JTG加固规范》中的增大截面加固受弯构件的计算公式提出了不同见解,如文献[7]。笔者在起草行业标准《城市桥梁结构加固技术规程》(以下简称《CJJ加固规程》)的过程中,对比分析这些计算方法的异同,并把原来两个规范中“仅在受拉区增大截面加固”的情况扩展到“受拉区、受压区同时增大截面”的通用情况,给出了《CJJ加固规程》中的计算表达式,最后用工程实例进行对比计算验证。
1 现行相关规范的规定 1.1 《JTG加固规范》《JTG加固规范》重点考虑了加固构件二次受力的因素影响,在矩形截面钢筋混凝土受弯构件的受拉区进行单侧增大截面抗弯加固时,其正截面受弯承载力的计算如图 1所示。

|
| 图 1 仅在受拉区增厚混凝土的矩形梁正截面抗弯承载力计算 Fig. 1 Calculation of bearing capacity on cross-section of rectangular beam strengthened with enlarged section only in tensile zone |
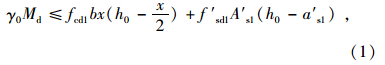
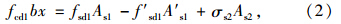
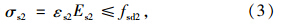

其中新增纵向普通钢筋的拉应变εs2按式(5)计算,截面应变图见图 1(c)。
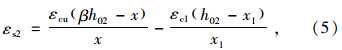
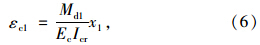
《GB加固规范》对于加固受弯构件正截面抗弯计算的规定与《JTG加固规范》不同,未在计算公式中特意强调构件的二次受力特征,而是根据试验结果,近似地按一次受力计算。为对比《JTG加固规范》,考虑混凝土强度等级不超过C50,另外将有关计算变量的表达式进行了修改,其正截面受弯承载力的计算公式如下:
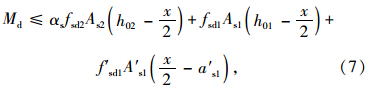

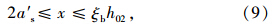
将《JTG加固规范》式(2)、式(3)及γ0=1.0代入式(1)中,得到:
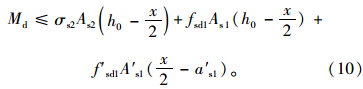
将式(10)与式(7)比较,两个公式基本相同,有以下两点不同之处:
(1)《GB加固规范》式(7)中h02和h01,在《JTG加固规范》的转换式(10)中全部用h0替代。从受力图式上分析,《GB加固规范》的公式应该更精确,但两者相差不大。
(2)在新增钢筋拉应力σs2的取值上有所不同,《JTG加固规范》的σs2是按式(3)和式(5)计算;而在《GB加固规范》中,σs2=αsfsd2,其中αs=0.9。
1.4 《JTG加固规范》计算方法讨论《JTG加固规范》体现了加固构件的受力特征,即两阶段受力,计算思路总体上是正确的,但有以下几个问题值得探讨:
(1)式(6)中的Md1应该为Mk1
《JTG加固规范》中,在第一阶段,原构件截面上边缘混凝土压应变εc1的计算弯矩是采用弯矩组合设计值Md1,而按开裂的钢筋混凝土弹性体弹性理论,此时的计算弯矩应采用初始荷载在原受弯构件验算截面上产生的弯矩标准值Mk1。文献[7]的作者也建议在加固前计算截面的恒载弯矩Md1应取标准值,而不是取组合设计值。
(2)式(3)的计算结果很单一,σs2的取值总是fsd2
通过大量的桥梁加固工程计算实例,发现按《JTG加固规范》计算时,得到的新增钢筋拉应变σs2=εs2Es2计算值均远远大于钢筋的抗拉设计强度fsd2。文献[7]中的计算实例得到的σs2=εs2Es2=400~800 MPa,而fsd2=280 MPa;文献[8]中的计算实例得到的σs2=εs2Es2=1 156 MPa,而fsd2=280 MPa。最终上面的计算实例σs2取值均为σs2=fsd2,这样就导致了很多计算过程失去意义,后文将具体分析原因。
(3)没有考虑加固构件受压区也新增混凝土的情况
《JTG加固规范》只考虑在截面受拉区单侧加厚混凝土的梁受弯承载力计算,而没有考虑构件同时在截面受拉区及受压区加厚混凝土的情况。
1.5 《GB加固规范》计算方法讨论《GB加固规范》中,在承载能力极限状态下,新增钢筋拉应力σs2=αsfsd2=0.9fsd2,计算公式简单明了,并且在绝大多数情况下与试验结果较为接近,虽然从理论上定性分析好像不太合理,但实际应用起来没有出现安全问题。从表面看,这个σs2的计算没有体现出加固构件的两阶段受力特征,与一次受力构件的计算无异,只是引入新增钢筋强度利用系数αs。这种做法是否安全和合理呢?可以从后面的加固受弯构件破坏形态研究中得出结论。
与《JTG加固规范》类似,《GB加固规范》也没有考虑矩形梁同时在受拉区及受压区加厚混凝土的情况,这个在即将颁布施行的《CJJ加固规程》中已补充完善。
2 有关专家建议的计算方法 2.1 文献[7]建议的方法(1)文献[7]建议的计算方法
基本参照《JTG加固规范》,但新增钢筋拉应变εs2按下列公式计算:
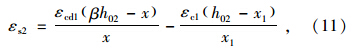
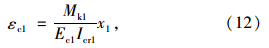
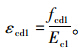
(2)对该计算方法的讨论
采用式(12)来计算εc1,即用Mk1取代《JTG加固规范》的Md1,从理论上讲是正确的;而式(11)用εcd1取代原《JTG加固规范》的εcu,这种做法不合理。
混凝土材料并不是理想的弹性材料,按文献[5]和文献[6],混凝土材料受压时,其应力-应变曲线有多种不同的计算图示,文献[4]及欧洲混凝土协会的标准规范均采用一条二次抛物线及水平线所组成的曲线,如图 2所示。

|
| 图 2 混凝土应力-应变曲线图 Fig. 2 Stress-strain curve of concrete |
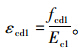 把混凝土作为一种理想的弹性材料,与混凝土实际的本构关系不符,且εcd1本身的物理意义比较抽象,缺乏理论依据。
2.2 杨炳成教授建议的方法
把混凝土作为一种理想的弹性材料,与混凝土实际的本构关系不符,且εcd1本身的物理意义比较抽象,缺乏理论依据。
2.2 杨炳成教授建议的方法(1)建议计算公式
长安大学杨炳成教授为《JTG加固规范》的主要起草人之一,在其进行该规范的宣贯及技术培训讲座中,杨炳成教授认为:钢筋混凝土结构按平衡设计或低筋设计时,承载能力均由原构件受拉钢筋控制。因而,εs2的计算采用原构件受拉钢筋达到设计值fsd1来控制,即求σs2时,宜采用容许应力法计算,依原构件截面上、下边缘应力分别为fcd1,fsd1控制。若原构件截面有效高为h01,受压区高度为x1,钢筋弹模为Es1;而增加材料后的组合截面,相应值为h02,x2,Es2时,则:
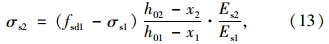
 为钢筋位置的影响系数。
为钢筋位置的影响系数。新增钢筋比原构件钢筋滞后一期载荷σs1,同步增长使原构件钢筋应力先达到设计值。如果原构件钢筋应变继续增加,虽然其应力停止增大,但存在着拉断的可能。新增钢筋的应力则有所放大(h02/h01) ,但随着σs1的值增大而减小,一般很难达到设计值fsd2。
(2)对该计算方法的讨论
对于杨炳成教授建议的计算公式(13),笔者认为此计算公式并不十分正确。式(13)成立的一个基本条件是:钢筋是理想的弹性材料,其应力-应变关系始终是呈直线比例关系。但钢筋材料只是在达到屈服强度之前是理想弹性材料,在达到屈服强度之后呈现塑性,见图 3。

|
| 图 3 钢筋应力-应变曲线图 Fig. 3 Stress-strain curve of steel reinforcement |
在极限状态下,虽然构件截面上的新、旧钢筋的应变是呈直线比例关系(平截面假定,见图 1(c),但其新、旧钢筋的应力并不能简单地认为与应变一样呈直线比例关系,而应根据钢筋材料的力学特性,分别计算其应力。大量试验结果证明,通常情况下,新、旧钢筋都可以达到各自的屈服强度,但按式(13)的计算结果,σs2是不可能达到其屈服强度的。
3 加固受弯构件破坏形态研究 3.1 几种可能破坏形态对于一次受力构件的正截面受弯承载能力极限状态的破坏形态有3类,分别为:适筋梁破坏(塑性破坏)、超筋梁破坏(脆性破坏)、少筋梁破坏(脆性破坏);而对于增大截面加固构件(二次受力构件),其破坏形态同样也存在这3类。由于加固构件在受拉区存在新、旧两种钢筋,从主观上分析,加固构件的适筋梁破坏这一类可能存在3种情况,分别为: A级适筋梁破坏是新、旧受拉钢筋均屈服的状态;B级适筋梁破坏是旧受拉钢筋屈服而新增受拉钢筋未屈服的状态;C级适筋梁破坏是新增受拉钢筋屈服而旧钢筋未屈服的状态。
这样,对于加固构件,共可能发生适筋梁破坏、超筋梁破坏(A级、B级、C级)、少筋梁破坏共5种破坏形态。针对仅在受拉区增大截面加固的单筋矩形梁,就这5种破坏形态分析如下:
(1)A级适筋梁破坏
其破坏过程如图 4所示,当原构件钢筋As1的拉应变刚刚达到屈服应变(对HRB335钢筋,εs1=εy1=0.001 4)时(即Ⅱa1阶段),此时构件并没有破坏,构件仍然可以承受更大的弯矩荷载,此时新增受拉钢筋As2的拉应变还没有达到屈服应变(εs2<0.001 4);当弯矩荷载继续增大时,原构件钢筋As1的拉应变继续增大,新增受拉钢筋As2的拉应变也达到其屈服应变(即Ⅱa2阶段,对HRB335钢筋,εs2=εy2=0.001 4);当弯矩荷载再继续增大时,原构件钢筋和新增钢筋的应变均进一步加大(但均应小于0.01),两者的拉应力均保持各自的屈服强度,依靠中和轴的上升(力臂的增大)来抵抗弯矩(Ⅲ阶段),直到受压区边缘混凝土压应变达到极限压应变εcu=0.003 3,梁进入第Ⅲa阶段,压区混凝土的抗压强度耗尽,压区混凝土出现纵向水平裂缝,随即混凝土被压碎,梁破坏。

|
| 图 4 增大截面加固的矩形梁正截面各阶段的应力应变图 Fig. 4 Stress-strain diagrams of cross-section of rectangular beam strengthened with enlarged section at different stages |
(2)B级适筋梁破坏
在原构件受拉钢筋达到屈服强度(在Ⅱa1阶段),随后随着弯矩增大,新增受拉钢筋还未达到其屈服强度,而受压区边缘混凝土的应变就已经达到极限压应变(在Ⅲa阶段)。B级适筋梁破坏比A级适筋梁破坏少了Ⅱa2、Ⅲ阶段。B级适筋梁破坏形态是否能实际发生,在下文深入探讨。
(3)C级适筋梁破坏
随着弯矩增大,原构件受拉钢筋尚未达到屈服强度,而新增受拉钢筋就已经达到其屈服强度,并随着截面弯矩的进一步增大,新增受拉钢筋保持其屈服强度不变而应变进一步增大,受压区边缘混凝土的应变就达到极限压应变(此时原构件受拉钢筋仍未达到其屈服强度)。由图 1(c)可大致看出,正常情况下旧钢筋拉应变εs1会大于新增钢筋拉应变εs2,这就意味着,当新增钢筋和旧钢筋为同品种钢筋时,新增钢筋屈服,旧钢筋也会屈服,故C级适筋梁破坏形态极其特殊,它有可能发生在加固后受压区高度x与加固前原截面有效高度h01之比x/h01大于原截面相对界限受压区高度ξb0的状态下。由于这个情况很特殊,不常见,在梁的正截面受弯承载力计算中,一般都认为原结构钢筋已经达到其抗拉强度设计值fsd1,即使未达到fsd1,其偏差也是很小的,故对C级适筋梁破坏不做深入研究,这种情况在《GB加固规范》第5.2.5条有涉及。
(4)超筋梁破坏
当原构件受拉区配筋率较大,且新增钢筋的配筋率很大时,旧钢筋和新增钢筋的应力增加缓慢,受压区混凝土首先达到极限压应变,此时旧钢筋和新增钢筋的应力均小于屈服强度。加固设计应避免出现超筋梁破坏,一般通过限制相对界限受压区高度来避免这种破坏形态。
(5)少筋梁破坏
加固设计应避免出现少筋梁破坏,与一次受力构件类似,可通过限制截面最小配筋率来避免这种破坏形态。
3.2 B级适筋梁破坏是否会发生《JTG加固规范》与《GB加固规范》中计算方法的差异最终可归结于一个关键问题——B级适筋梁破坏是否能够实际发生。
从图 4来分析,当B级适筋梁达到Ⅱa1阶段后,新增受拉钢筋没有达到其屈服强度时,构件仍然可以稳定地承受弯矩的进一步增加(因为新增钢筋应力σs2可稳定地增大),构件全截面仍处于稳定承载状态,此时构件并没有破坏;弯矩增加到一定程度,随着中性轴的上升,加固构件截面受压区边缘达到极限压应变,构件破坏,如果受拉区新增钢筋仍未达到其受拉强度,则可以认为这种加固设计其实是超筋设计。
故从定性角度分析,B级适筋梁破坏使得新增钢筋没有充分发挥其抗拉强度,可认为是浪费钢筋,其实质是超筋设计,加固设计时宜避免此种情况。
B级适筋梁破坏形态通常也不会发生的一个原因是:虽然新增钢筋相对于旧钢筋存在应变滞后,但这个应变滞后量远小于旧钢筋屈服平台上的应变长度。对HRB335钢筋,其屈服平台上应变长度将近0.02。设计规范为安全起见,规定钢筋极限拉应变0.01,这样HRB335钢筋屈服平台上的应变长度(图 3)为εsu-εy=0.01-0.001 4=0.008 6。而新旧钢筋的应变滞后量肯定小于εy1=0.001 4,这样钢筋屈服平台的应变长度是其应变滞后量的0.008 6/0.001 4=6.1倍,故旧钢筋在达到其屈服应变(εy1=0.001 4)后,有足够的应变空间来等待新增钢筋也达到其屈服应变(εy2=0.001 4)。
3.3 相关文献的表述在结构加固的诸多文献资料中,有很多是关于一次受力与二次受力问题的研究,但他们的观点有明显的分歧。对于增大截面加固受弯构件,有的认为二次受力对结构的影响显著,有的认为其影响可忽略不计。
文献[1]的条文说明中提到:试验结果表明,正截面受弯破坏时,两种受力性质的新增主筋均能屈服。因此,不论哪一种受力构件,均可近似地按一次受力计算。
文献[9]得到的结论:加固后的适筋梁,其极限抵抗弯矩可以不考虑二次受力计算。
文献[10]通过试验得出的结论:二次受力条件下,采用增大截面法加固能有效地提高梁的极限荷载和刚度,其极限荷载受初始荷载等级的影响较小。增大截面加固梁的荷载-挠度曲线在二次荷载作用下,一般有4个工作阶段,分别为增大截面部分混凝土开裂、上下层纵向受拉钢筋先后屈服、最后梁达到极限荷载宣告破坏。
通过以上的定性分析和综合相关文献的表述,可这样认为:进行增大截面加固的受弯构件,只要保证必要的构造措施,原有的受拉纵筋以及新增加的受拉纵筋都能先后达到各自的屈服强度,新旧钢筋的承载力都可以得到充分的利用。增大截面加固受弯构件的二次受力特征主要体现在正常使用极限状态,比如挠度、裂缝宽度等;而在承载能力极限状态中,二次受力受弯构件可近似按一次受力计算。
4 《CJJ加固规程》中的计算方法《CJJ加固规程》送审稿已经通过了专家审查,很快将颁布实施。《CJJ加固规程》对增大截面加固矩形截面受弯构件的正截面受弯承载力计算规定如图 5所示。

|
| 图 5 增大截面加固矩形截面受弯构件的正截面抗弯承载力计算 Fig. 5 Calculation of bearing capacity on cross-section of rectangular beam strengthened with enlarged section |
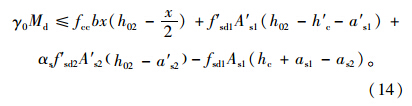
混凝土受压区高度x应按下列公式确定:
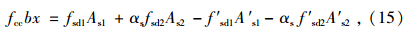
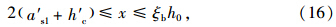
某受弯构件为双筋矩形截面,截面尺寸b1×h1=300 mm×400 mm。采用C25混凝土,纵向钢筋采用HRB335级钢筋。跨中截面配置纵向受拉钢筋为4B22(As1=1 520 mm2),as1=45 mm,受压钢筋为2B12(A′s1=226 mm2),a′s1=40 mm,见图 6。由于荷载等级提高,跨中截面弯矩组合设计值为M=150 kN·m。I类环境条件,安全等级为二级。请验算原梁跨中截面抗弯承载能力。如不满足要求,拟在受拉区采用增大截面进行加固,新增混凝土强度等级为C30,新增钢筋采用HRB335钢筋。加固层厚度设为150 mm,跨中截面第一阶段弯矩组合设计值Md1=80 kN·m,第二阶段弯矩组合设计值Md=170 kN·m。试对跨中新增截面进行配筋设计,并对加固截面的承载力进行复核。(注:本例引自文献[8]例2-1)

|
| 图 6 计算实例(单位:mm) Fig. 6 Calculation example (unit: mm) |
分别采用不同规范、规程中的计算方法,得出的计算结果见表 1。
| 计算方法 | 加固配筋设计 |
加固后截面受弯 承载力复核 | ||||
|
x计算 值/mm |
新增钢 筋计算 面积 As2 /mm2 |
选配 钢筋 |
选配钢 筋的 截面积 As2 /mm2 |
x值/ mm |
抗弯承 载力Mu/ (kN·m) | |
| 《JTG规范》 | 126.8 | 268 | 2B14 | 308 | 164.7 | 191.3 |
| 《GB规范》 | 128.5 | 323 | 2B16 | 402 | 134.3 | 169.1 |
| 《CJJ规程》 | 135.0 | 410 | 3B14 | 462 | 138.8 | 174.8 |
| 注:《CJJ规程》未颁布 | ||||||
从表 1可看出,不同的规范公式计算的结果有所差别,相对来讲,采用《CJJ加固规程》推荐的计算方法,计算结果相对更安全,计算过程比《JTG加固规范》简便,无需用到Md1,无需计算为在Md1作用下的原构件截面上边缘混凝土压应变εc1。
6 结论 6.1 两阶段受力特征的理解(1)加固构件确实具有两阶段受力特征,其两阶段受力特征表现在两个方面,一方面是时间上,旧钢筋与新增钢筋的应变应力的增长过程存在时间差;另一方面是应变量上,在同一时刻,新增钢筋与旧钢筋的应变量不同,正常情况下新增钢筋的应变值会小于旧钢筋。总体来讲,新增钢筋相对旧钢筋存在应变滞后、应力滞后。
(2)新增钢筋相对于旧钢筋存在应变滞后,在带载加固的情况下,一般新增钢筋的总应变值小于旧钢筋,即εs2<εs1;但新增钢筋的应力应变滞后只是一个时间上的滞后或较小的应变值,而按照适筋梁设计原则,极限状态下,新增钢筋应该也达到其屈服强度,此时旧钢筋可能在时间上更先一步达到屈服强度,并在屈服平台上已经发生一定的应变值。
(3)应从适筋梁破坏形态的研究中来理解加固构件的两阶段受力,并不能从直观感觉上认为新增受拉钢筋应变滞后将导致新增钢筋达不到其设计抗拉强度。文献[7]及杨炳成教授建议的计算方法,均是假定旧钢筋刚好达到其屈服强度,再利用新旧钢筋的应变比例关系来计算新增钢筋的应变及应力,这类方法是不可取的。
6.2 承载能力极限状态的理解(1)增大截面加固时,当加固后的构件出现以下现象之一时,即可认为构件达到了承载能力极限状态:
极限状态一:原构件的混凝土或新增混凝土的压应变达到了极限压应变,即εc=εcu=0.003 3;
极限状态二:原构件钢筋或新增钢筋的拉应变达到了钢筋的极限拉应变,即εs1=0.01或εs2=0.01。
(2)极限状态一包括了本文3.1所述的A级适筋梁、B级适筋梁、C级适筋梁、超筋梁这4种破坏形态;极限状态二其实就是本文3.1所述的少筋梁破坏。
(3)梁加固设计的破坏状态应该为塑性破坏,也就是适筋梁破坏,并且只发生A级适筋梁或C级适筋梁。增大截面加固梁通常都是A级适筋梁,C级适筋梁是特殊情况。而B级适筋梁的根本性质可归结为“超筋设计”,浪费钢筋,加固设计宜避免。
| [1] | GB 50367—2013,混凝土结构加固设计规范 [S]. GB 50367—2013, Code for Design of Strengthening Concrete Structure [S]. |
| [2] | JTG/T J22—2008,公路桥梁加固设计规范 [S]. JTG/T J22—2008,Specifications for Strengthening Design of Highway Bridges [S]. |
| [3] | JTG D62—2004,公路钢筋混凝土及预应力混凝土桥涵设计规范 [S]. JTG D62—2004,Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts [S]. |
| [4] | GB 50010—2010,混凝土结构设计规范 [S]. GB 50010—2010,Code for Design of Concrete Structures [S]. |
| [5] | 叶见曙. 结构设计原理 [M]. 北京:人民交通出版社,2007. YE Jian-shu. Structure Design Principle [M]. Beijing:China Communications Press,2007. |
| [6] | 过镇海,时旭东. 钢筋混凝土原理和分析 [M]. 北京:清华大学出版社,2004. GUO Zhen-hai,SHI Xu-dong. Principle and Analysis of Reinforced Concrete [M]. Beijing:Tsinghua University Press,2007. |
| [7] | 陈焕勇,单成林,梁立农,等. 论现行规范中有关增大截面加固受弯构件的设计原理 [J]. 工程抗震与加固改造,2010,32(2):87-90,111. CHEN Huan-yong,SHAN Cheng-lin,LIANG Li-nong,et al. Research about the Design Principle of Flexural Member Strengthened with Reinforced Concrete for Existing Codes[J]. Earthquake Resistant Engineering and Retrofitting,2010,32(2):87-90,111. |
| [8] | 邬晓光,白青侠,雷自学. 公路桥梁加固设计规范应用计算示例[M]. 北京:人民交通出版社,2011. WU Xiao-guang,BAI Qing-xia,LEI Zi-xue. Application and Calculation Examples of Specifications for Streng-thening Design of Highway Bridges [M]. Beijing:China Communications Press,2011. |
| [9] | 刘思孟. 二次受力对钢筋混凝土梁式桥加固后的承载力与破坏形态分析研究 [C]// 第20届全国结构工程学术会议论文集(第Ⅱ册).北京:工程力学杂志社,2011:449-453. LIU Si-meng. Research on Bearing Capacity and Failure Modes of RC Beam Bridge after Strengthening under Secondary Loading Condition [C]//Proceedings of the 20th National Structural Engineering Conference (Ⅱ). Beijing:Engineering Mechanics Press,2011:449-453. |
| [10] | 袁广林,徐媛媛. 二次受力条件下增大截面加固梁的试验研究 [J]. 山东科技大学学报:自然科学版,2007,26(5):40-45. YUAN Guang-Lin,XU Yuan-yuan. Experimental Research on the Beams Strengthened by Section Enlargement under Secondary Loading Condition[J]. Journal of Shandong University of Science and Technology:Natural Science Edition,2007,26(5):40-45. |
| [11] | 程源. 增大截面法加固钢筋混凝土梁的二次受力分析 [D]. 广州:华南理工大学,2010. CHENG Yuan. Analysis on Secondary Stress of Reinforced Concrete Beams by the Method of Enlarging Section [D]. Guangzhou:South China University of Technology,2010. |
| [12] | 郭智刚. 增大截面加固桥梁构件的设计方法研究 [D].南京:东南大学,2008. GUO Zhi-gang. Study on Design Methods of Bridge Member Strengthened with Section Enlargement[D]. Nanjing:Southeast University,2008. |
| [13] | 谌洁君. 外包混凝土加固结构的受力性能与工程应用 [D]. 上海:同济大学,2009. CHEN Jie-jun. Load-bearing Performance and Engineering Application of Structure Strengthened with Surrounding Concrete [D]. Shanghai:Tongji University,2009. |
| [14] | 张树仁,王宗林. 桥梁病害诊断与改造加固设计 [M]. 北京:人民交通出版社,2006. ZHANG Shu-ren,WANG Zong-lin. Bridge Disease Diagnosis and Reinforcement Design [M]. Beijing:China Communications Press,2006. |
| [15] | 单成林,梁立农,陈焕勇. 混凝土梁式桥加固设计理论及试验 [M]. 北京:科学技术文献出版社,2011. SHAN Cheng-lin,LIANG Li-nong,CHEN Huan-yong. Theory and Experiment of Reinforcement Design of RC Girder Bridge [M]. Beijing:Science and Technology Literature Press,2011. |
 2015, Vol. 31
2015, Vol. 31
