扩展功能
文章信息
- 胡柏学, 黄浩, 曾威
- HU Bo-xue, HUANG Hao, ZENG Wei
- 基于健康监测的悬索桥吊索疲劳可靠性评估
- Assessment of Fatigue Reliability for Hanger Cables of Suspension Bridge Based on Health Monitoring
- 公路交通科技, 2015, Vol. 31 (6): 76-80
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (6): 76-80
- 10.3969/j.issn.1002-0268.2015.06.012
-
文章历史
- 收稿日期:2014-06-16
2. 长沙理工大学 桥梁安全控制省部共建教育部重点实验室, 湖南 长沙 410114
2. Key Laboratory of Bridge Safety Control of Ministry of Education, Changsha University of Science and Technology, Changsha Hunan 410114, China
悬索桥上部结构的主要承重构件是悬挂并锚固于两侧索塔的缆索,而吊索作为缆索与主梁的联力构件是悬索桥最重要的构件之一。吊索在运营期间的状态直接关系到悬索桥的安全性能,若一根吊索发生破坏,会引起全桥其他吊索受力产生变化,从而出现局部失稳,影响桥梁结构安全。在我国现有的服役桥梁中,部分桥梁仅运营3~5 a便出现拉索病害或断索事故[1]。因此,对悬索桥吊索状况的监测十分必要。桥梁结构健康监测系统是一个以桥梁结构为对象,以自动化实时监测为特征,集现代传感、通信网络和计算机技术为一体的综合监测系统。通过对不同构件的参数实时采集监控,能及时、准确地为桥梁运营管养提供可靠的结构状态信息,是一种先进、可靠的检测手段。国外从20世纪80年代就已开始建立大量的桥梁健康监测系统,如丹麦GreatBeltEast悬索桥[2]、挪威Skarnsundet斜拉桥[3]、英国Flintshire独塔斜拉桥[4]的健康监测系统,通过健康监测系统对桥梁运营阶段的位移、变形、拉索索力等参数进行了实时监控。我国桥梁健康监测起步较晚,但从20世纪90年代中开始发展十分迅速[5, 6],至目前为止,桥梁结构健康监测技术已趋于成熟并被工程界所重视,国内许多重点桥梁工程都已建立了健全的结构健康监测系统[7]。
本文以吉茶高速矮寨特大桥为例,介绍了健康监测系统在悬索桥吊索安全性能跟踪观测中的应用。针对矮寨大桥8根长吊索进行了健康监测系统的安装,通过对吊索应力长期监控数据的分析,研究了桥梁上、下游对称位置索力测试值的偏差,从而验证了监测系统的有效性和精度。在测试数据的基础上,对吊索疲劳寿命的可靠度展开了详细探讨。
1 矮寨大桥吊索健康监测矮寨悬索桥为吉茶高速公路的控制性工程,全桥设计为塔梁分离式地锚式悬索桥,主缆的孔跨布置为 (242+1 176+116) m。中跨主缆采用1/9.6的垂跨比,主索中心距为27 m,采用平面索布置。全桥采用71对吊索,吊索标准间距为14.5 m。
根据对矮寨大桥易损性分析的结果来看[8],两侧索塔附近的长吊索索力变化幅值最大,因此,对大桥4对长吊索进行索力实时健康监测。被测吊索抗拉强度1 870 MPa,直径88 mm,理论计算截面积3 977 mm2。测点布置位置如图 1所示。测点编号J为吉首岸吊索,C为茶峒岸吊索;第2位数字代表被测吊索编号,第3位数为0代表该吊索位于上游一侧,1代表位于下游一侧(表 1)。

|
| 图 1 吊索健康监测布置(单位:cm) Fig. 1 Health monitoring arrangement of hanger cables(unit: cm) |
| 编号 | 吊索自由长度/m | 距跨中位置/m | 备注 |
| J-10 | 98.780 | 522 | 岩锚吊索 |
| J-11 | 98.780 | 522 | 岩锚吊索 |
| J-20 | 89.650 | 493 | 主梁吊索 |
| J-21 | 89.750 | 493 | 主梁吊索 |
| C-10 | 42.776 | 536.5 | 岩锚吊索 |
| C-11 | 49.773 | 536.5 | 岩锚吊索 |
| C-20 | 84.513 | 478.5 | 主梁吊索 |
| C-21 | 84.511 | 478.5 | 主梁吊索 |
本系统吊索索力的健康监测采用加速度传感器测振法。安装中将加速度传感器用索夹或绑带固定在斜拉索上,通过对振动时程数据进行傅里叶变换获得拉索振动频率,然后根据拉索频率与索力的理论公式换算出索力。
2 吊索监测数据分析基于建立的吊索索力健康监测系统(图 2),本文采集了矮寨大桥在正常运营期间内1个月的索力监测数据并加以分析。

|
| 图 2 索力监测仪 Fig. 2 Hanger cable monitor |
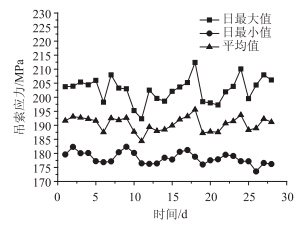
以吊索J-10和J-11为例,筛选出1个月内每日所监测到的索力最大值、最小值和平均值,绘制成吊索应力极值时程曲线,如图 3、图 4所示。
|
| 图 3 吊索J-10应力极值时程曲线 Fig. 3 Stress-time curves of hanger cable J-10 |
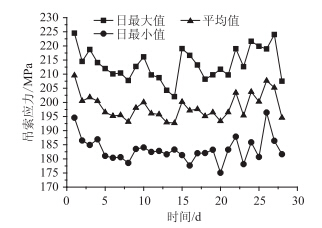
|
| 图 4 吊索J-11应力极值时程曲线 Fig. 4 Stress-time curves of hanger cable J-11 |
由图 3和图 4可知,矮寨大桥在正常运营的1个月内,被测吊索应力日极值和均值变化趋势基本保持一致。但是,J-10和J-11为上、下游对称位置的吊索,测量的索力存在一定偏差,最大偏差为7.6%。为了判别桥梁上、下游两侧吊索索力是否平衡,对上、下游所有被测吊索应力日均值总和进行了对比,其应力时程曲线如图 5所示。
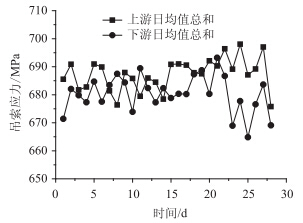
|
| 图 5 上、下游被测吊索应力日均值总和时程曲线 Fig. 5 Curves of sum of daily average stress vs. time of measured upstream and downstream hanger cables |
从图 5可以发现,上、下游所有被测吊索应力日均值总和与J-10、J-11那样的单对吊索相比,索力测量的偏差要小很多,最大偏差为2.9%。可以推断,若考虑全桥71对吊索,则上游索力总和与下游索力总和近似相等,上、下游索力保持平衡。
3 吊索疲劳寿命预测随着悬索桥跨度和交通流量的不断增加,吊索的疲劳性能逐渐成为研究的热点。疲劳是材料或构件在循环加载下,在某点或某些点产生的局部永久性损伤,并在若干循环次数之后形成的结构内裂纹,或使裂纹进一步扩展直到完全断裂。局部应力集中是造成吊索疲劳破坏的主要原因,由反复循环荷载的特性和次数所决定。对吊索疲劳寿命的分析,一般采用基于S-N曲线的疲劳寿命评估方法。
基于S-N曲线的疲劳寿命评估方法建立在大量的常幅疲劳试验数据之上,根据MINER累计损伤定律进行损伤度计算以确定构件的使用寿命。疲劳寿命为疲劳失效前经历的应力或应变循环次数,一般用N表示。在一定的应力σ之下,在不同应力幅Δσ的常幅应力下进行疲劳试验,测出构件断裂时对应的疲劳寿命。
矮寨大桥的吊索材料为镀锌钢丝绳,公称抗拉强度为1 870 MPa。参照文献[9],我国1860级低松弛钢绞线的S-N曲线表达式为:
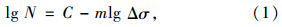
对式(1)两边取对数变换可得:
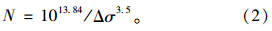
从1个月内采集的矮寨大桥吊索索力监测数据中筛选出被测索力的日极值(图 3和图 4)。现以d为单位,对正常运营状态下桥梁吊索的疲劳应力幅值Δσ进行估计。本文对于吊索疲劳寿命的计算采用测得数据中的最不利状态,因此吊索的疲劳应力幅值简化为应力最大值减去平均值的常幅应力:
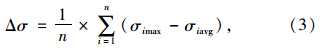
将式(3)代入式(2),可得到基于健康监测系统数据的正常运营期间吊索疲劳寿命:
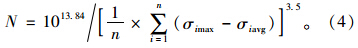
以J-10吊索为例,将计算出的吊索应力幅值(统计期为28 d)代入式(4),可得J-10号吊索在桥梁正常运营期的疲劳寿命N=1.933 7×109 次(见表 2)。
| 编号 | 疲劳寿命/(×109 次) | 编号 | 疲劳寿命/(×109 次) |
| J-10 | 1.933 7 | C-10 | 0.676 4 |
| J-11 | 1.021 6 | C-11 | 2.314 0 |
| J-20 | 2.796 1 | C-20 | 6.738 3 |
| J-21 | 1.155 8 | C-21 | 4.222 6 |
结构可靠度是指结构在规定时间内和规定条件下完成预定功能的概率。悬索桥在实际运营过程中,反复荷载会对吊索造成疲劳损伤,而疲劳损伤的过程是逐渐积累的,且不可逆地单调增加。因此,本文在考虑疲劳损伤累积的基础上,对吊索疲劳寿命的失效概率进行计算。一些疲劳试验表明,在一定应力范围内,疲劳寿命分布符合对数正态分布或Weibull分布,而考虑到疲劳损伤累积过程采用Weibull分布更合适[10]。文献[11]根据Weibull分布的概率密度函数得到结构在(0,N)时间内不发生疲劳破坏的概率为:
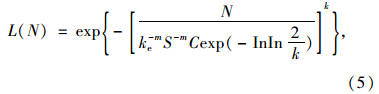
式中,N为结构疲劳寿命; ke为反映应力强度大小的系数;S为应力幅值; C=1013.84;k为形状因子,k=VN-1.08,其中变异系数VN取均值0.53。
考虑上式中应力幅值S,由于桥梁结构在运营期间所承受的车辆荷载是随机的,因此,吊索在一般情况下也受到变幅交变应力。根据损伤度相等的原则,可将变幅交变应力循环转化为常幅等效应力的重复作用。将Se定义为等效应力幅值,则:
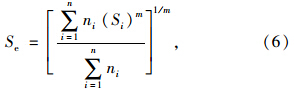
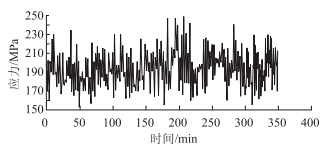
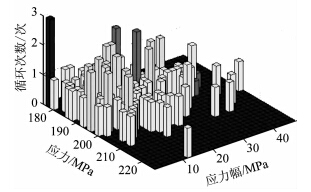
根据健康监测系统所采集到的吊索应力时程曲线上的各点数据,运用雨流计数法对应力时程曲线进行统计分析,计算出应力幅值频数,从而计算得出等效应力幅值,代入式(5),求得各吊索的疲劳可靠度。同样以J-10吊索为例,由健康监测系统采集到的应力时程曲线,通过Matlab进行雨流计数法分析。图 6为J-10号吊索在被测24 h内的应力时程曲线。图 7为雨流计数法算得的应力幅统计图。
|
| 图 6 J-10吊索24 h应力时程曲线 Fig. 6 Twenty-four h stress-time curve of hanger cable J-10 |
|
| 图 7 吊索应力幅雨流法统计图 Fig. 7 Statistical chart of stress amplitude of hanger cables by rain flow counting method |
根据雨流法计数的结果,将不同应力幅值水平下的频次代入式(6),可得吊索J-10的等效应力幅值Se=10.365 MPa。代入式(5),其中疲劳寿命N取前面计算结果1.933 7×109,得到疲劳可靠概率为0.999 999 35。由可靠指标与失效概率的对应关系[12],根据内插法可得出吊索J-10疲劳可靠指标为4.988 451。
表 3列出了矮寨大桥被测吊索基于健康监测系统的疲劳可靠指标。可以看出,被测吊索在车辆荷载作用下经历约109次循环的疲劳可靠指标较高,基本保持在4~5左右。考虑到吊索数据测试时间为2014年初,属于通车初期,桥梁在运营初期车流量不大,吊索受力也未达到正常使用水平,测试得到总体数据偏小。因此,对于疲劳寿命和疲劳可靠指标的计算结果与实际相比都偏保守,随着桥梁车流量的增大甚至达到饱和,其计算结果会稍有变化。
| 编号 | 疲劳可靠指标 | 编号 | 疲劳可靠指标 |
| J-10 | 4.988 451 | C-10 | 5.006 565 |
| J-11 | 5.003 307 | C-11 | 4.979 595 |
| J-20 | 4.966 124 | C-20 | 4.762 597 |
| J-21 | 4.289 597 | C-21 | 4.911 644 |
(1) 健康监测在悬索桥吊索索力的监测中能发挥较好的作用,能可靠地采集到索力的实时状态。通过连续监测数据的分析,得到了基于健康监测系统数据的对称位置吊索的测量偏差,通过上、下游索力总和的推算,认为监测到的数据趋于平衡。
(2) 利用S-N曲线对矮寨大桥吊索疲劳寿命进行了预测,通过1860级低松弛钢绞线的S-N曲线得到了基于健康监测的连续数据采集下的吊索疲劳寿命预测模型。利用吊索日最大应力幅值作为常幅应力的最不利状态,计算得出了各被测吊索的疲劳寿命。
(3)利用雨流计数法对被测吊索等效应力幅值进行了统计分析,基于分析结果得到了吊索疲劳寿命可靠度,认为吊索在桥梁运行初期具有足够的疲劳可靠性。根据可靠度指标可以判断在未来随着桥梁车流量不断增大,在正常使用范围内吊索均能满足运营要求。
| [1] | 胡俊,欧进萍.风载作用下悬索桥吊索腐蚀疲劳寿命分析[J].钢结构,2011,26(5):63-67. HU Jun,OU Jin-ping. The Corrosion Fatigue Life Analysis on Hangers of Long Span Suspension Bridge under Wind Load[J].Steel Construction,2011,26(5):63-67. |
| [2] | PEDERSEN A E Y. Structural Monitoring of the Great Belt East Bridge[C]//Proceedings of the Third Symposium on Strait Crossing. Rotterdam: Balkema,1994:54-62. |
| [3] | MYROLL F,DIBIAGIO E. Instrumentation for Monitoring the Skarnsunder Cable-stayed Bridge [C]//Proceedings of the Third Symposium on Strait Crossing. Rotterdam: Balkema,1994: 207-215. |
| [4] | CURRAN P,TILLY G. Design and Monitoring of the Flintshire Bridge,UK [J]. Structural Engineering International,1999,9 (3):225-228. |
| [5] | 秦权.桥梁结构的健康监测[J].中国公路学报,2000,13(2):37-42. QIN Quan. Health Monitoring of Long-span Bridges[J].China Journal of Highway and Transport,2000,13(2):37-42. |
| [6] | 李惠,周文松,欧进萍,等.大型桥梁结构智能健康监测系统集成技术研究[J].土木工程学报,2006,39(2):46-52. LI Hui,ZHOU Wen-song,OU Jin-ping,et al. A Study on System Integration Technique of Intelligent Monitoring System for Soundness of Long-span Bridges[J].China Civil Engineering Journal,2006,39(2):46-52. |
| [7] | 缪长青,李爱群.瀛洲大桥结构健康监测系统设计[J].公路交通科技,2011,28(8):104-110. MIAO Chang-qing,LI Ai-qun. Design of Structural Health Monitoring System for Yingzhou Bridge[J]. Journal of Highway and Transportation Research and Development,2011,28(8):104-110. |
| [8] | 余崇.矮寨大桥基于性能的地震易损性分析[D].长沙:湖南大学,2013. YU Chong. Performance-based Seismic Fragility Analysis of Aizhai Bridge[D].Changsha:Hunan University,2013. |
| [9] | 马林.国产1860级低松弛预应力钢绞线疲劳性能研究[J].铁道设计标准,2000,20(5):21-23. MA Ling. Fatigue Performance of 1860 MPa Low Relaxation PC Strands[J].Railway Standard Design,2000,20(5):21-23. |
| [10] | 程育仁,缪龙秀,侯炳麟.疲劳强度[M].北京:中国铁道出版社,1990. CHENG Yu-ren,MIAO Long-xiu,HOU Bing-lin. Fatigue Strength[M].Beijing:China Railway Press,1990. |
| [11] | 杨靓. 悬索桥吊索寿命期内动态可靠性分析[D]. 长沙:湖南大学,2009. YANG Liang. Dynamic Reliability Analysis on Hangers of Suspension Bridge during Lifetime[D]. Changsha:Hunan University,2009. |
| [12] | 赵国藩,金伟良.结构可靠度理论[M].北京:中国建筑工业出版社,2000. ZHAO Guo-fan,JIN Wei-liang. Structural Reliability Theory[M].Beijing:China Building Industry Press,2000. |
 2015, Vol. 31
2015, Vol. 31
