扩展功能
文章信息
- 王凌波, 蒋培文, 马印平, 赵煜
- WANG Ling-bo, JIANG Pei-wen, MA Yin-ping, ZHAO Yu
- 桥梁静载试验校验系数及优化评定方法研究
- Study on Verification Coefficient and Optimization Evaluation Method of Bridge Static Load Test
- 公路交通科技, 2015, Vol. 31 (6): 62-68
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (6): 62-68
- 10.3969/j.issn.1002-0268.2015.06.010
-
文章历史
- 收稿日期:2014-07-02
2. 陕西省交通厅基本建设工程质量监督站, 陕西 西安 710075
2. Basic Construction Project Quality Supervision Station, Shaanxi Transport Department, Xi'an Shaanxi 710075, China
桥梁荷载试验是目前我国常用的桥梁检测方法之一,当通过桥梁调查与检算分析尚不足以评定桥梁承载力时,可采用荷载试验测定桥梁的实际工作状况,结合桥梁调查、检测与检算来评定桥梁的实际承载能力[1]。荷载试验一般包括静载试验和动载试验。静载试验主要通过在桥梁结构上施加与设计荷载或使用荷验荷载基本相当的外载,测试桥梁结构的控制截面在各级试作用下的挠度、应力等特性的变化,通过校验系数(实测值与理论值的比值)来评定结构的实际承载能力;动载试验则主要是通过汽车的行车、跳车等方式产生激振来测试桥梁结构各控制部位的动挠度、动应变及其模态参数,以反映桥梁的整体工作性能[2]。
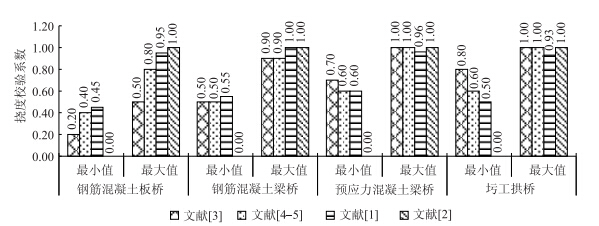
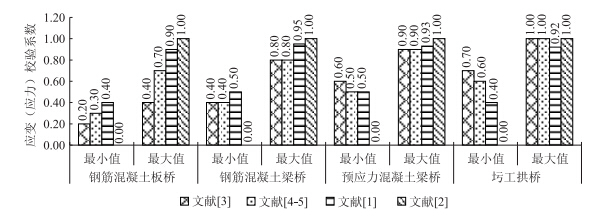
校验系数是桥梁静载试验评定的重要参数,对于不同桥梁结构校验系数的取值,国内各参考文献及规范所推荐的范围存在较大差异。1988年《公路旧桥承载能力鉴定方法(试行)》[3]、2004年《公路桥梁承载能力检测评定规程(报批稿)》[4]、2007年《公路旧桥承载力评定方法及工程实例》[1]、2011年《公路桥梁承载能力检测评定规程(JTG/T J21—2011)》[2]、2012年《公路桥梁荷载试验规程(报批稿)》[5]等规范及文献均提出了桥梁静载试验校验系数常值范围。对比发现,以上文献提出的校验系数均局限于钢筋混凝土板桥、钢筋混凝土梁桥、预应力混凝土桥及圬工拱桥等4种简单结构,且校验系数取值有较大差异,如图 1及图 2所示。
|
| 图 1 挠度校验系数对比 Fig. 1 Comparison of verification coefficients of deflection |
|
| 图 2 应变(应力)校验系数值对比 Fig. 2 Comparison of verification coefficients of stress and strain |
近年来诸多学者对校验系数进行了相关研究。2003年长安大学许汉铮对大跨径悬索桥静载试验进行研究,得到悬索桥吊索的校验系数应在0.90~1.00附近[6];2009年福建工程学院叶建峰通过分析及测试大跨径悬索桥的吊索索力,提出悬索桥吊索校验系数范围应为0.90~1.10[7];2013年长安大学于明策以连续箱梁为研究对象,认为应变仅是桥梁局部状况的反映且易受外部环境影响,挠度校验系数更能真实反映桥梁结构的工作状态[8];2011年西南交通大学施嘉以大溪河三号桥为工程背景,通过对比分析认为实际圬工拱桥的校验系数普遍小于《公路旧桥承载能力鉴定方法》中所规定的常值[9];2012年华东交通大学刘旭政提出斜拉桥主梁、拉索、主塔的校验系数合理取值范围[10];2013年华南理工大学司徒毅研究了影响应变校验系数的随机参数,获取应变校验系数的统计特性及评估指标信息[11];2011年长安大学刘利军运用概率统计方法分析了不同桥梁荷载试验下挠度校验系数和应变校验系数以及加载效率与校验系数的关系,并给出了桥梁结构正常校验系数的取值范围[12];2011年长安大学王凌波以常用横向分布系数计算方法为分析手段,提出不考虑校验系数影响的基于挠度值的刚度分解法和考虑校验系数影响的基于挠度比值的刚度分解法[13];2006年合肥工业大学石飞停考虑了桥梁施工的随机性和结构的对称性针对具体工程实例将各种工况下结构控制截面的实际变形或者应力同理论计算值进行了比较,并计算了结构的校验系数[14]。
查阅规范及以上参考文献,追溯校验系数的起源问题,均被告知校验系数是基于实测与数理统计的方法所得到的经验系数,并没有详尽的理论依据、推导过程及各桥型校验系数范围差异较大的原因解析。且各文献中的校验系数取值表均仅针对于钢筋混凝土板桥、钢筋混凝土梁桥、预应力混凝土桥和圬工拱桥4个较模糊的大类,对于具体桥型,跨径、梁高等参数均无任何限定。从理论上分析研究各桥型校验系数范围差异的原因对在役桥梁检评技术的发展有着重大工程意义和实用价值。近年来,对于采用荷载试验评判桥梁实际承载能力状态的做法在业界褒贬不一,焦点集中在对评判方法的评定结果与实际承载力状况的吻合度上,因此本文针对桥梁静载试验校验系数范围的理论估算方法及评定时的误判概率进行了分析。
1 校验系数常值范围理论估算方法
当理论计算模型与实际结构完全吻合时,实测值与理论值应十分接近,而在工程实践中,实际结构的各种特性均难以精确模拟。对桥梁荷载试验中校验系数范围的理论研究,归根究底就是对各种难以精确考虑而忽略的影响因素进行合理估算,并综合考虑得到桥梁荷载试验中校验系数的理论估算范围。结合工程实践的特点及建模计算中忽略的因素,计算模型与实际结构的偏差可归于3个方面(以下统称为校验系数影响因子),如表 1所示。
| 序号 | 1 | 2 | 3 |
| 偏差产生原因 | 建模分析时通常进行了合理简化,桥面板、桥面铺装、护栏、横隔板及齿板、各种受力钢筋及构造钢筋的刚度、预应力筋的刚度等因素通常情况下均不予考虑,但以上因素均对桥梁实际刚度有增大作用。 | 有限元分析、平截面假定等计算方法产生的合理误差,结构尺寸、材料特性取值的偏差、支座及连接处难以精确模拟等原因,造成理论值与计算值存在一定偏差。 | 桥梁荷载试验建模分析中未考虑混凝土开裂、钢筋锈蚀、结构整体工作性能较差等因素,导致结构计算刚度大于实际桥梁的刚度,无法正确反映桥梁结构的实际工作状态。 |
| 对结果的影响 | 造成理论计算挠度(应变)值大于实测值。 | 造成理论计算挠度(应变)值与实测值产生不确定偏差,可偏大或偏小。 | 造成理论计算挠度(应变)值小于实测值。 |
| 对应系数 | 模型简化系数α(模型简化使校验系数产生的偏差) | 计算误差系数β(计算误差使校验系数产生的偏差) | 工作状态系数γ(工作状态使校验系数产生的偏差) |
| 对应范围 |
α∈[a1,a2] αs=a2-a1 |
β∈[b1,b2] βs=b2-b1 |
γ∈[c1,c2] γs=c2-c1 |
| 校验系数η | η=1+α+β+γ∈[1+a1+b1+c1,1+a2+b2+c2] | ||
基于目前校验系数的评定方法可以看出,不同桥型对应的校验系数常值范围有较大偏差且并不接近于1,可说明校验系数计算时是由以上3个校验系数影响因子共同作用的综合结果。表 1中各校验系数影响因子的影响因素较多,精确的变化范围及概率分布十分复杂,均有待进一步研究。但各校验系数影响因子的大致范围,可根据工程经验进行统计,以钢筋混凝土梁桥挠度校验系数为例,模型简化系数α的范围估算可将桥面板、铺装层、护栏、钢筋及预应力筋的刚度效应等因素对主梁刚度的影响通过测试统计,近似转化为主梁截面顶板增加 9~11 cm。对于钢筋混凝土梁桥,通过该转化可按式(1)建模计算模型简化系数α范围,亦可按式(2)的回归公式近似计算模型简化系数α范围(其中h为主梁原始梁高)。

计算误差系数β根据工程经验近似取[-0.05,0.05],工作状态系数γ根据工程经验近似取[0,0.10],根据以上估算范围,以钢筋混凝土及预应力混凝土梁桥为例,进行挠度校验系数范围的推算,如表 2所示(其中模型简化系数α按式(2)近似计算)。
| 钢筋凝土板桥 | 钢筋混凝土梁桥 | 预应力混凝土梁桥 | ||||
| 最小值 | 最大值 | 最小值 | 最大值 | 最小值 | 最大值 | |
| 常用跨径/m | 6 | 13 | 8 | 20 | 20 | 50 |
| 常用梁高/m | 0.4 | 0.8 | 0.6 | 1.5 | 1 | 3 |
| 模型简化系数α | -0.56 | -0.34 | -0.45 | -0.24 | -0.34 | -0.17 |
| 计算误差系数β | -0.05 | 0.05 | -0.05 | 0.05 | -0.05 | 0.05 |
| 工作状态系数γ | 0 | 0.1 | 0 | 0.1 | 0 | 0.1 |
| 校验系数1+α+β+γ | 0.39 | 0.81 | 0.50 | 0.91 | 0.61 | 0.98 |
根据以上估算范围,以钢筋混凝土及预应力混凝土梁桥为例,进行挠度校验系数范围的推算(其中模型简化系数α按式(2)近似计算)。
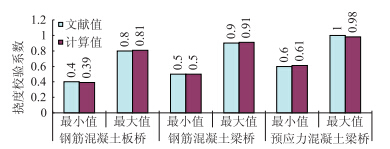
将表 2计算结果与应用较为广泛的文献[4, 5]中相应桥型的挠度校验系数范围进行对比,结果如图 3所示。
|
| 图 3 挠度校验系数范围对比 Fig. 3 Comparison of verification coefficients for deflection |
由图 3可见,本文计算的校验系数理论值与当前文献中通过大量试验统计得到的校验系数常值吻合良好,计算偏差在5%以内。该方法可用于估算各 种桥梁结构的荷载试验校验系数理论范围,并根据推算流程可以得到以下一些规律:
(1)对于中小跨径梁桥,模型简化系数α对校验系数的影响较大,且梁高越小时模型简化系数α影响越大,校验系数通常偏小;对于平均梁高3 m以上的大跨径连续梁桥、连续刚构桥,模型简化系数α产生的影响较小,结构校验系数应偏大。
(2)对于预制场的中小跨径裸梁进行荷载试验分析时,由于其不包含桥面铺装等构造,模型简化系数α接近于0,整体校验系数偏大,不建议采用规范中的范围进行结构承载力判定。
(3)对于复杂体系大跨径桥梁,例如斜拉桥、悬索桥、拱桥等结构,模型简化系数α的影响不大,整体校验系数应偏大。
(4)对于钢结构主梁或钢桥,校验系数影响因子应考虑与钢筋混凝土桥梁的区别予以修正或换算,不宜直接套用钢筋混凝土桥梁的校验系数范围及其计算方法。
经对比发现以上推论与实桥测试及研究文献所反映出的规律完全吻合,再次说明本文假定及理论分析方法符合实际情况,准确性较高。由于受到钢筋混凝土结构实际工作状态下的裂缝分布影响,在实际工程中应变测试数据往往离散程度较大,本文上述分析均采用较为稳定可靠的挠度校验系数,桥梁构件在部分开裂状态下关于应变校验系数的分析还有待进一步研究。
2 校验系数评定时的误判概率分析
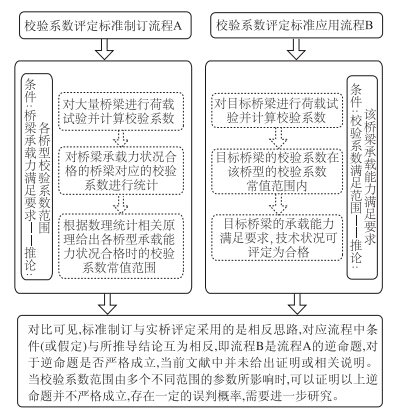
对于目前的桥梁静载试验评定体系,现行规范的制定与实际桥梁检评技术之间存在互逆的关系,如图 4所示。众所周知,当一个原命题成立时,其逆命题未必成立,需要严密的证明,而目前的文献关于该问题的研究十分少见,本节对该问题进行分析研究。
|
| 图 4 校验系数制订与应用关系图 Fig. 4 Relationship between verification coefficient determination and its application |
传统的校验系数受到本文提出的3个校验系数影响因子的共同作用,而反映结构状态的参数主要是工作状态系数,应由工作状态系数是否在正常范围内来评价结构的实际工作状态。基于表 1给出的桥梁校验系数计算假定,对图 4所示的逆命题进行误判概率分析。由于校验系数影响因子的具体范围和概率分布对于不同参数桥梁均不相同,在此初步使用两种常见计算假定来计算误判概率:一种将校验系数影响因子等因素在计算时直接采用范围叠加,最终采用常见的均匀分布假定即区间长度比例计算概率(分布假定1);另一种假定校验系数影响因子在其对应区间内服从置信度为99.7%的正态分布(分布假定2)。两种方法对应的误判概率计算流程见表 3,两种假定下的误判概率变化趋势见图 5~图 6。
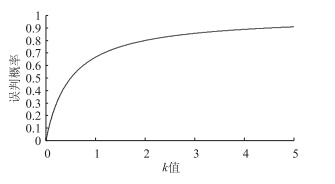
|
| 图 5 范围直接叠加时的误判概率 Fig. 5 Misjudgement probability of scope superposition |
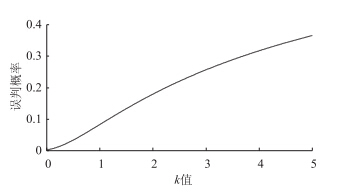
|
| 图 6 服从正态分布时的误判概率 Fig. 6 Misjudgement probability subject to normal distribution |
由图 5~图 6可以看出,无论采用哪种校验系数影响因子的分布假定,除了k=0(即模型简化系数与计算误差系数变化范围均为0)时的误判概率为0,其余情况在评定时均无法避免的存在一定的误判概率,误判概率随k值的增大而增大,且校验系数影响因子的概率分布方式及k值对误判概率有很大的影响。为了使桥梁评定结果尽可能准确,应结合被评定桥梁的实际参数,研究减小目标桥梁k值的实用方法,从而最大程度的减小误判概率。除了以上两种常见概率分布假定外,同样可以假定校验系数影响因子服从均匀分布或三角分布,此类分布的误判概率不易给出计算公式,可利用数值模拟方式求得数值解,以下给出具体算例。
3 桥梁静载试验优化评定算例分析
根据第2节的分析,为了最大程度地减小桥梁评定时的误判概率,可通过优化建模方法、细化参数取值等手段,将模型简化系数及计算误差系数变化为固定数值或使其缩小至较小的范围,从而减小通过校验系数直接判定桥梁状态时的误判概率,提高桥梁荷载试验评定的准确度。通过一个跨径16 m、梁高1.3 m钢筋混凝土T梁的算例,对比研究优化评定方法与传统评定方法,见表 4。
| 传统评定方法 | 优化评定方法 | |
| 模型简化系数α | 不考虑桥面板、铺装层、护栏、钢筋及预应力筋的刚度效应等因素对主梁刚度的影响,模型简化系数α范围取表 3计算值,即[-0.45,-0.24] | 按表 2方法,建模将主梁顶板增加9~11 cm并计算模型简化系数α,或通过式(2)近似计算模型简化系数得 α∈[-0.29,-0.26] |
| 计算误差系数β | [-0.05,0.05] | 可通过混凝土强度、结构尺寸的实测值来修正计算模型,使计算误差系数β接近[-0.03,0.03] |
| 工作状态系数γ | [0,0.1] | [0,0.1] |
| 校验系数判定范围 | [0.50,0.91] | [0.68,0.87] |
| 误判概率 | 0.86(仅考虑区间,k=3.10) | 0.64(仅考虑区间,k=0.90) |
| 0.38(影响因子正态分布,k=5.41) | 0.03(影响因子正态分布,k=0.45) | |
| 0.628(影响因子均匀分布) | 0.221(影响因子均匀分布) | |
| 0.485(影响因子三角分布) | 0.08(影响因子三角分布) |
由表 4可以看出,本文优化评定方法主要分为3个部分,理论值修正计算、校验系数范围优化分析、采用修正后的桥梁校验系数,结合优化的校验系数范围进行桥梁评定。从评定流程及评定结果可以看出,虽然评定流程中存在着一些难以确定的估算因素及相关假定,但通过并不繁琐的细化计算,可以较大程度地提高桥梁静载试验评定结果的准确性(校验系数影响因子实际分布复杂,有待进一步研究,但在不同的计算假定下,误判概率均可降低0.2以上)。对于复杂体系桥梁无法使用表 2中的简化公式时,可按同样思路建模计算模型简化系数等参数,从而得到该桥型的校验系数范围并进行评定及误判概率计算。该方法简明实用,效果良好,适合在桥梁静载试验评定中推广使用。
4 结论
(1)针对传统桥梁静载试验校验系数评定方法的优化问题,提出校验系数影响因子的概念及校验系数范围的理论估算方法,可对不同参数、不同结构形式桥梁的校验系数范围进行理论估算,弥补现行标准中桥型较单一、无法对具体桥型进行校验系数范围估算的不足之处。
(2)基于校验系数影响因子假定,提出校验系数评定时误判概率的概念及其计算方法,并提出降低误判概率的实用方法。
(3)以某钢筋混凝土梁桥为对象,对传统评定方法和本文优化评定方法进行对比,本文优化评定方法可较大程度地提高桥梁静载试验评定结果的准确性和可靠性,适合在桥梁静载试验评定中推广使用。
| [1] | 张劲泉.公路旧桥承载力评定方法及工程实例[M].北京:人民交通出版社,2007. ZHANG Jin-quan. Evaluating Method and Project Example of Bearing Capacity of Existing Highway Bridges[M]. Beijing:China Communication Press,2007. |
| [2] | JTG/T J21—2011,公路桥梁承载能力检测评定规程[S]. JTG/T J21—2011, Specification for Inspection and Evaluation of Load-bearing Capacity of Highway Bridge[S]. |
| [3] | 谌润水,胡钊芳.公路桥梁荷载试验[M].北京:人民交通出版社,2003. CHEN Run-shui, HU Zhao-fang. Loading Test for Highway Bridges[M].Beijing:China Communications Press,2003. |
| [4] | JTG/T J21—2011,公路桥梁承载能力检测评定规程[S]. JTG/T J21—2011, Specification for Inspection and Evaluation of Load-bearing Capacity of Highway Bridge[S]. |
| [5] | 宋龙龙.桥梁荷载试验校验系数影响因素分析[D].西安:长安大学,2014. SONG Long-long. Analysis of Inflencing Factors of Bridge Load Testing Structural Verification Coefficient[D].Xi'an:Chang'an University,2014. |
| [6] | 许汉铮,黄平明,杨炳成.大跨径悬索桥静载试验研究[J].公路,2003(9):1-7. XU Han-zheng,HUANG Ping-ming,YANG Bing-cheng. Research on Static Load Test of Long Span Suspension Bridge[J]. Highway,2003(9):1-7. |
| [7] | 叶建峰,颜桂云,江星.大跨径悬索桥静载试验研究[J].山东理工大学学报:自然科学版,2009,23(3):8-13. YE Jian-feng,YAN Gui-yun,JIANG Xing. Research on Static Load Test of Long-span Suspension Bridge [J]. Journal of Shandong University of Technology:Natural Science Edition,2009,23(3):8-13. |
| [8] | 于明策,李金亮.基于MIDAS应变与挠度校验系数的对比分析[J].现代交通技术,2013,10(6):30-32. YU Ming-ce,LI Jin-liang. Comparative Analysis of Strain and Deflection Calibration Coefficient Based on MIDAS[J]. Modern Transportation Technology,2013,10(6):30-32. |
| [9] | 施嘉,杨永清,余华丽.圬工拱桥承载能力评估分析[J].西南公路,2011(4):141-144. SHI Jia,YANG Yong-qing,YU Hua-li. Bearing Capacity Evaluation of Masonry Arch Bridge [J] Southwest Highway,2011(4):141-144. |
| [10] | 刘旭政,王丰平,黄平明.斜拉桥各构件校验系数的常值范围[J].长安大学学报:自然科学版,2012,32(1):57-61. LIU Xu-zheng,WANG Feng-ping,HUANG Ping-ming. Verification Coefficient Constant Range of Cable-stayed Bridges Components [J]. Journal of Chang'an University:Natural Science Edition,2012,32(1):57-61. |
| [11] | 司徒毅. 预应力混凝土单片梁静载试验应变校验系数随机分析及评估指标研究[D].广州:华南理工大学,2012. SITU Yi. Research on Stochastic Analysis and Evaluation Index of Strain Verification Coefficient of Static Test on Prestressed Concreted Monolithic Beam [D].Guangzhou:South China University of Technology,2012. |
| [12] | 刘利军.梁桥静载试验结果评定分析[D].西安:长安大学,2011. LIU Li-jun. Analysis of Beam Bridge Static Load Test Result Evaluation[D]. Xi'an:Chang'an University,2011. |
| [13] | 王凌波.在役预应力梁桥残余承载力评估方法研究[D].西安:长安大学,2011. WANG Ling-bo. Research of Residual Bearing Capacity Assessment Method of In-service Prestressed Concrete Girder Bridges[D]. Xi'an:Chang'an University,2011. |
| [14] | 石飞停. 基于荷载实验的预应力混凝土连续梁桥检测与应用研究[D].合肥:合肥工业大学,2006. SHI Fei-ting. Research of Detection and Application of Prestressed Concrete Continuous Girder Bridge Based on Loading Test[D]. Hefei:Hefei University of Technology,2006. |
 2015, Vol. 31
2015, Vol. 31

