扩展功能
文章信息
- 刘瑜, 邵旭东
- LIU Yu, SHAO Xu-dong
- 轻型组合梁桥面板在日照作用下温度梯度效应研究
- Research on Temperature Gradient Effect of Light-weighted Composite Bridge Deck under Solar Radiation
- 公路交通科技, 2015, Vol. 31 (6): 54-61
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (6): 54-61
- 10.3969/j.issn.1002-0268.2015.06.009
-
文章历史
- 收稿日期:2014-07-28
钢和混凝土的温度线膨胀系数基本上相同,但是由于钢的导热系数大,传热快,而混凝土的导热系数相对较小,对外界环境温度的变化反应也相对较慢,因此外界温度的变化会造成钢梁与混凝土板之间存在温差,从而在钢梁和混凝土板中引起温度应力。而确定其应力值大小必须先得出其合理的温度梯度模式。根据已有的一些研究,如Zuk[1],Emanuel,Hulsey[2],Kennedy和 Soliman[3]等对组合梁桥温度梯度的研究成果可以得出,在组合梁桥上部结构中,混凝土桥面板温度沿其截面高度方向呈梯度分布,而钢梁中温度则为均匀分布。由于先前的温度梯度的研究都是在厚度较大的普通混凝土的基础上开展的,其混凝土铺装层厚度基本上都是200 mm 以上,而对于轻型组合梁桥,当采用超高性能混凝土时,混凝土的厚度大大减小,故需要确定其对应的温度梯度模式和正确的温度基数,为轻型组合梁桥的温度应力计算提供依据。
1 轻型组合梁桥
轻型组合梁桥的主要结构形式是正交异性钢桥与薄层超高性能混凝土(Ultra-High Performance Concrete,以下都简称UHPC)通过抗剪连接件连接成整体,形成组合结构[4]。采用超高性能混凝土时,其导热系数比一般普通水泥混凝土的导热系数更低,与沥青铺装层的导热系数的差异较大,因此不管是在UHPC层,还是在两种面层中必然会出现较为明显的温度梯度。因此在对轻型组合梁桥进行全面的研究中,温度梯度及相应内力和应力计算是必不可少的一个方面。
2 热传导分析 2.1 太阳辐射计算
导致UHPC层升温的太阳辐射[5]是一个非常复杂的系统,它与具体时间下的太阳高度角、目标处的海拔高度、当地的纬度、大气质量系数和大气透明度等多种因素有关。归纳起来,目标表面接收到的太阳辐射强度主要来自3个方面:太阳直射、太阳散射和地面太阳反射辐射。从文献[6]可以看出,对于桥面板的太阳辐射主要取决于太阳高度角这一具体因素,一年中太阳辐射的最大值发生在天气晴朗无云的夏季,而一天之中辐射强度的最大值出现在中午12点左右。 2.2 混凝土外表面与外界的总热流交换
根据混凝土箱梁外表面的热平衡方程,可以得出由UHPC层外表面向UHPC层内的传热量q0计算表达式如下:
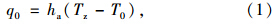

大量实践经验表明,结构外界的热环境按第三类边界条件来模拟是最为合适的。在第三类边界条件中,求解域周围流体的温度和求解域边界与周围流体间的表面传热系数在实际工程当中体现为结构边界的综合温度Tz和结构边界与外界的综合换热系数ha。
3 算例验证
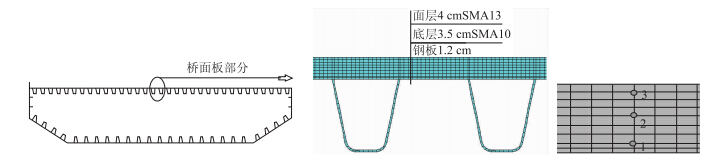
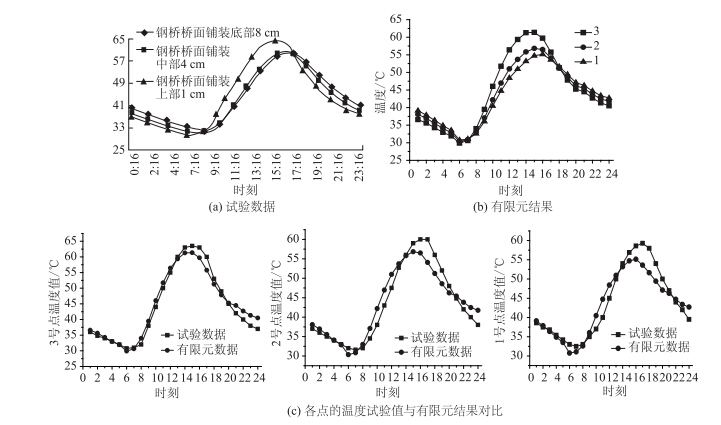
根据已有的温度场的分析研究,可以发现在准确模拟截面边界条件的前提下,采用有限元ANSYS分析其温度场是可行的。本文以文献[7]为例,对重庆市鹅公岩大桥桥面铺装层温度进行计算,钢箱梁截面划分网格后的截面模型及具体测点布置如图 1所示。其中1号点位于铺装层底部,检测钢板温度;2号点位于钢桥桥面铺装中部4 cm处;3号点位于钢桥桥面铺装上部1 cm处。在进行温度场的计算过程中,各参数与文献相同,且在文中钢箱梁内部空气几乎不流动,视为优良的隔热层。图 2(a)为试验数据曲线,图 2(b)为有限元分析计算结果。图 2(c)列出了不同位置处点的试验数据与有限元之间的温度曲线图。
|
| 图 1 鹅公岩大桥截面及温度测试点 Fig. 1 Cross-section of Egongyan bridge and temperature measuring points |
|
| 图 2 试验数据和有限元数据 Fig. 2 Comparison of test data and finite element analysis data |
从图 2(c)中可知,试验数据和有限元分析结果存在偏差,这是因为在温度场分析中,涉及到诸多参数,如综合换热系数的取值及其随时间的变化,大气温度和箱内的理论值与真实值的偏差等,均会整体影响温度场的计算结果,使两者之间存在一定的偏差。具体比较图 2(c)中3个对比曲线可得到偏差值均在5 ℃左右。同时对比图 2(a)和图 2(b)的最大温差可知,在下午13:00时刻计算结果与文献中的试验数据的温差均达到最大值,均在8 ℃左右。故采用ANSYS有限元分析软件分析温度梯度是可行的。
4 温度梯度计算
MCCLURE[8]等在1984年试验数据的基础上已经证实了混凝土结构纵向和横向的温度变化很小,故桥梁中的三维热流问题可以简化为一维状态的热传递,即沿组合梁桥截面高度的竖向温度变化。选择夏季某一无云微风的晴天的大气环境计算,当UHPC层受到日照作用时,表面温度迅速升高,但由于热量向混凝土内部传递的速度较慢,从而使外表面和内部的温度变化速率存在较大的差异,内部的温度变化明显滞后于外表面处的温度变化,这样就在UHPC层中产生较大的竖向温差。计算主要步骤如下:
4.1 定义单元类型和材料属性
本文轻型组合梁地理位置处于北纬20°,东经110°,平均风速为1 m/s,大气透明度系数为0.656。我国所处纬度范围内,不同地区的最大辐射一般都出现在夏季,这里取8月18号作为计算日期。在Ansys温度场分析中,单元类型选用plane55单元模拟,混凝土表面总热交换系数ha的采用文献[9]取值,有限元分析中材料的一些参数如表 1所示。
| 材料 | 钢材 | UHPC层 | 铺装层 |
| 比热容/[J·(kg·K)-1] | 520 | 1 046 | 1 168 |
| 热传导系数/[(W·m·K)-1] | 48 | 1.95 | 1.5 |
| 密度/(kg·m-3) | 7 850 | 2 700 | 2 400 |
| 热吸收率 | 0.9 | 0.65 | 0.9 |
| 热膨胀系数 | 1.2e-5 | 1e-5 | 1e-5 |
| 泊松比 | 0.3 | 0.2 | 0.2 |
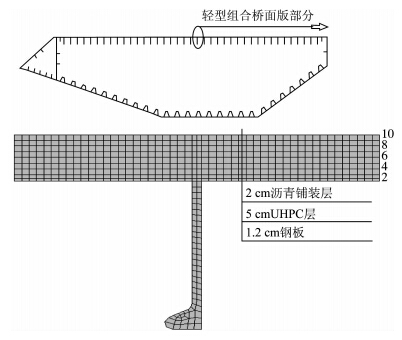
在Ansys有限元分析中,组合截面的尺寸及UHPC层和沥青铺装层温度控制点如图 3所示。根据已有的研究可知,沥青混凝土铺装层的厚度对UHPC层的温度梯度具有一定的折减。然而从热传导参数来看,沥青混凝土铺装层的热吸收能力明显大于UHPC层。在现有规范的温度梯度模式中,沥青混凝土铺装层的厚度为50 mm和100 mm,然而在UHPC-正交异性组合桥面板温度分布中,铺装层厚度为10~40 mm,小于50 mm。在本文的工程实例中,铺装层厚度取值为20 mm,UHPC层厚度取值50 mm。计入沥青铺装层时温度梯度控制点从下至上为1~10,不计沥青铺装层时温度梯度控制点从下至上为1~8。
|
| 图 3 组合截面及轻型组合桥面板部分 Fig. 3 Composite section and part of light-weightedcomposite bridge deck |
采用ANSYS有限元分析软件,按照第三类边界条件的加载模式对其进行了温度时程仿真分析。时程范围为某年8月18号00:00—24:00,UHPC层厚度为50 mm。由于UHPC的厚度很薄,当分析桥梁上部结构的竖向最大温差时,可只考虑UHPC顶板上的太阳热辐射和热对流,及钢箱梁顶板底面的内部热对流。由于缺乏实际的测量数据,其大气温度表达式采用的是1978年 Kreith 和 Kreider[10]提出的正弦函数曲线分布公式,表达式如(3)所示:
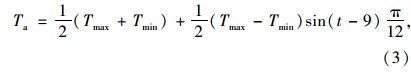
在有限元分析中,应该先确定箱梁内的空气温度,具体分析过程中:先不考虑箱梁内的对流换热,将空气层模拟出来,得到钢箱梁顶板底下的空气温度,接着在考虑箱梁内的综合换热系数基础上,将先前求解出来的箱梁内的温度以边界条件的形式加载上去。其中以无铺装层时的温度为例,其温度分布如图 4所示。
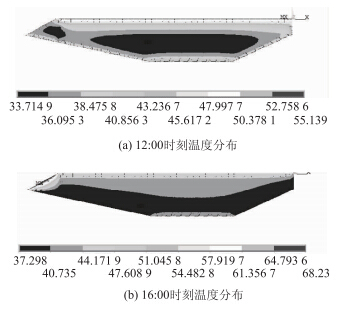
|
| 图 4 不同时刻温度分布(单位:℃) Fig. 4 Temperature distributions at different time(unit:℃) |
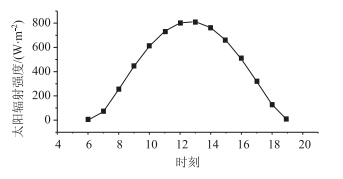
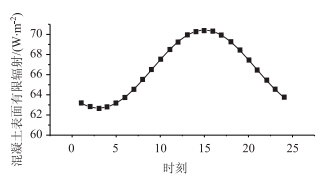
按照已有的混凝土温度场理论,通过有限元APDL编辑的命令流计算所得的边界条件,如太阳辐射强度曲线和UHPC表面有效辐射强度如图 5、图 6所示为正弦函数分布。同时计入沥青铺装层和不计沥青铺装层的各控制点的温度随时间的变化规律如图 7所示,也服从正弦函数分布,这与文献[11]的结论相符。
|
| 图 5 太阳辐射强度 Fig. 5 Solar radiation intensity |
|
| 图 6 混凝土表面有效辐射 Fig. 6 Effective radiation on concrete surface |
|
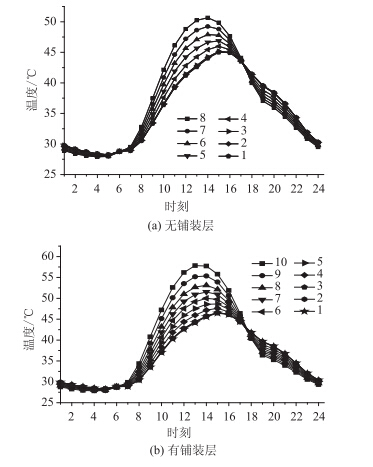
| 图 7 无铺装层与有铺装层时控制点的温度时程曲线 Fig. 7 Temperature time history of control points with/without pavement |
从图 7可以看出不考虑铺装层和考虑铺装层时,UHPC层的温差都在正午12:00达到最大值,各控制点的温度在13:00时刻达到最大。分析其原因:沥青铺装层有一定的厚度,对热量的传递有一定的滞后作用,下面层UHPC的导热系数较低,加之 50 mm 的厚度,更加延缓了热量的传递,因此出现了上述现象。一般来说,混凝土桥面板出现最大板厚温差的时刻要早于该板外表面温度峰值时刻。这是由于随着大气温度的增加,钢箱梁的导热快,箱梁内空气温度不断升高,使得竖向温度梯度减小,故在温度最大时刻,温差反而降低。
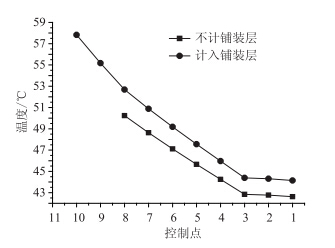
可分别从图上提取出12:00时刻时的温差值作为最大温度梯度的根据。轻型组合梁截面的各控制点的最大温度和最大温差如图 8、图 9所示。
|
| 图 8 控制点的最大温度 Fig. 8 Max temperatures of control points |
|
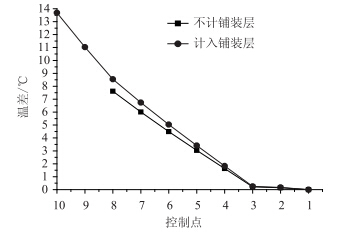
| 图 9 控制点的最大温差 Fig. 9 Max temperature differences of control points |
从图 8、图 9可知,当不考虑铺装层的影响时,整个截面的温度分布为二折线形式,UHPC层温度呈线性分布,钢梁内温度几乎为均匀分布,50 mm 厚度的UHPC层的最大温差为7.62 ℃;当考虑铺装层的影响时,整个截面的温度分布为三折线形式,铺装层和UHPC层各自呈线性分布,钢梁内仍为均匀分布。其中,由于沥青铺装层的热传导系数小于UHPC层,其温差直线斜率较UHPC层的直线斜率更大,温度梯度更明显。这与Naruoka等学者[12]对日本大阪简支组合梁桥Shigita桥的温度方面的试验结论也是一致的。且UHPC层的温度和温差分布与无磨耗层时的趋势一致,但是UHPC层的温度值整体高于无铺装层时的温度值。从图 9可以看出,不计入20 mm的沥青铺装层时,UHPC层的温差最大值为7.62 ℃;计入沥青铺装层时,整个截面的温度梯度为13.69 ℃,其中沥青铺装层的温差最大值为5.16 ℃,UHPC层的温差最大值为8.55 ℃。由此可知,当只关注结构层UHPC的温度时,计入沥青铺装层后,其吸热能力的增大作用大于其厚度对温度的折减作用,故反而增加UHPC的温度值和温差值。
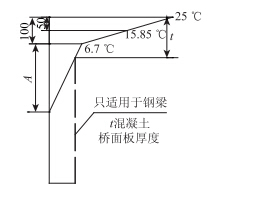
Carl Berwanger 和 Yaroslav Symko[13]在1974年研究中,采用0.354比例的试验模型,其混凝土桥面板厚59.31 mm (2.421 in),由测得的试验数据得到稳态热传导下的最大温差值为5 ℃(9.1 F)。对比前面有限元瞬态分析的温差来看,瞬态热传导分析所得结果高于稳态热传导下的最大温差,这与热传导理论相一致。这也说明采用有限元分析软件ANSYS分析得到的温度梯度是可行的,得出的温度梯度结果也是可采取的。结合我国《公路桥涵设计通用规范》[14],如图 10和表 2所示,当UHPC层厚度为50 mm 时,T1=25 ℃,内插取值可得T2=15.85 ℃,温差值为9.15 ℃,较前面有限元计算结果偏保守。综上可得,在混凝土厚度为50 mm时轻型组合梁的温度梯度取计入铺装层时的最大温差8.55 ℃,故在轻型组合梁的设计中,温度梯度荷载如图 11所示。
|
| 图 10 规范温度梯度(单位:mm) Fig. 10 Specified temperature gradient (unit: mm) |
| 铺装类型 | T1/℃ | T2/℃ |
| 混凝土铺装 | 25 | 6.7 |
| 50 mm沥青混凝土铺装 | 20 | 6.7 |
| 100 mm沥青混凝土铺装 | 14 | 5.5 |
从规范中表格的数据可知,当考虑沥青铺装层厚度时,温度梯度减小,而在前面的有限元分析中,当考虑铺装层时温度梯度是增大的, 但两者之间并不矛盾。我们应该注意到规范中铺装层的厚度是50 mm,而轻型组合梁中铺装层厚度只有20 mm,铺装层厚度越大对温度梯度的折减程度越大。同时沥青混凝土铺装层的热吸收率大于UHPC层的吸热率, 铺装层的热物理参数能增大温度梯度。故存在一个临界铺装层厚度,使得当铺装层的厚度达到该临界厚度时,由铺装层热物理参数引起的对UHPC层温度梯度的放大和由厚度引起的对UHPC层温度梯度的折减两者完全抵消。根据已有的研究如文献[8],一般临界铺装层厚度取50 mm。因此在本文中当铺装层厚度为20 mm时,由铺装层热物理参数引起的对UHPC层温度梯度的放大程度大于由厚度引起的对UHPC层温度梯度的折减程度,整体上增大了UHPC层温度梯度。因此在轻型组合梁温度梯度取值时,对现有取值可适当增加12%左右。
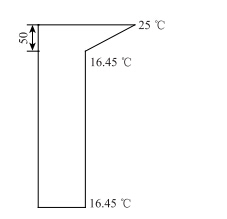
|
| 图 11 温度梯度(单位:mm) Fig. 11 Temperature gradient (unit: mm) |
本研究对琼州海峡3 000 m悬索桥方案进行了系统深入的研究,本文对其中的钢-UHPC组合桥面方案的温度效应展开了以下研究工作。其中3 000 m悬索桥布置如图 12所示。
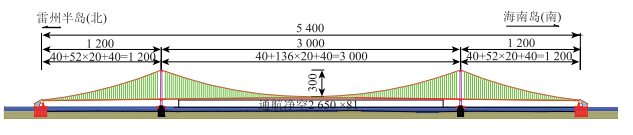
|
| 图 12 悬索桥的立面图(单位:m) Fig. 12 Elevation of suspension bridge (unit:m) |
其主梁采用轻型组合梁,正交异性板的加劲肋形式为开口的球扁肋。双幅主梁,中间采用钢横梁连接。主梁为双向10车道,汽车荷载采用公路一级,计入1.15倍的冲击系数和1.15倍的汽车偏载系数。二期恒载取值55 kN/m。横断面如图 13所示。
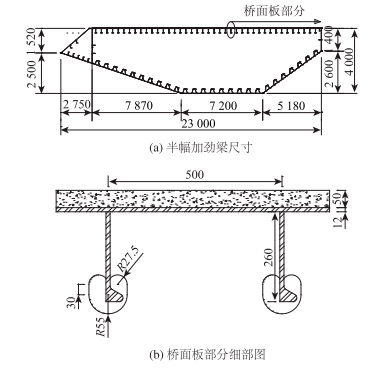
|
| 图 13 加劲梁横截面(单位:mm) Fig. 13 Cross-section of stiffening girder (unit:mm) |
采用有限元分析软件进行全桥整体受力分析。其中单元数2 469,节点数2 196,主缆和吊杆采用只受拉桁架单元模拟,钢箱梁和UHPC层都采用梁单元模拟,两者之间通过弹性连接中的刚性连接模拟,UHPC层和钢梁之间位移完全耦合,变形保持一致。主塔与主梁相交处采用刚度为2×106 kN/m的一般弹性连接约束作为横桥向的弹性抗风支座。根据悬索桥的计算理论,首先计算得出初始平衡状态,使整个结构在恒载作用下的线形与目标线形一致,在此基础上进行温度效应和汽车荷载效应计算。其中温度梯度通过有限元分析中梁截面温度来模拟,即在梁单元横截面UHPC层的顶部和底部施加对应的温度值,对于横截面UHPC层其他位置处,有限元分析中自动采用线形内插,如此来模拟UHPC层的温度梯度;对于钢梁部分,采用梁单元温度施加均匀的温度值。本文重点关注UHPC层在温度荷载和汽车荷载作用下的应力值,如图 14所示。
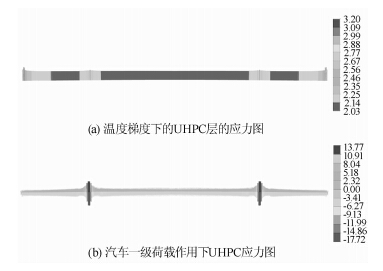
|
| 图 14 不同工况下UHPC层应力图(单位: MPa) Fig. 14 Stresses of UHPC layer under differentconditions (unit:MPa) |
从图 14上可以发现在温度梯度作用下,全桥范围内UHPC层的拉应力变化不大,其平均值约为2.4 MPa。然而在汽车荷载作用下,由于主塔处吊杆间距为边跨和中跨吊杆间距的4倍,从而使主塔处主梁节段上UHPC层拉应力值很快达到最大值,除了桥塔处,在全桥范围内UHPC层拉应力值分布也是比较均匀的,基本在5.0 MPa左右。对于边跨加劲梁端部由于添加的约束跟实际的还是存在差异,由圣维南原理可知,模拟的约束对加劲梁端部附近的梁单元的应力值影响较大,距离端部越远时,影响越小,因此加劲梁的端部及其附近的应力值没有很大的参考价值。
结合上面UHPC的应力图,可以看到UHPC层在温度梯度作用下的最大拉应力值达到2.4 MPa,对于普通混凝土而言很可能已经达到甚至超过其抗拉强度设计值。对比两者结果可知,除了在桥塔处主梁节段上温度梯度作用下UHPC的最大拉应力值与汽车荷载作用下的值相差较大外,在全桥范围内温度效应约占汽车荷载效应的50%。对于考虑了汽车冲击系数和偏载系数的双向10车道的汽车一级荷载作用而言,温度梯度作用效应达到约其一半的值,这说明温度梯度的效应不可忽视,故有必要研究轻型组合梁在温度梯度下的效应。
6 结论
(1)采用ANSYS有限元分析软件,取夏季某一晴空天气条件,分析24 h内轻型组合桥面体系的温度时程曲线,提取出其最大温差值,得出轻型组合梁UHPC的竖向温度呈线性分布。将有限元计算的结果与已有的研究比较,可知分析所得的结果是可靠的。进一步将所得的最大温差与我国现行规范对比,规范对轻型组合梁的温度梯度值偏保守。
(2)对比了不考虑沥青混凝土铺装层和考虑沥青混凝土铺装层时UHPC层的最大温差。计算结果表明,考虑铺装层时的UHPC温差更大,沥青铺装层增大了UHPC层的温度梯度值,这与我国现行桥梁规范不一致,因此轻型组合梁桥面板的温度分析中应进入铺装层的影响,对UHPC层的温度梯度适当增大。
(3)对主跨3 000 m的悬索桥进行有限元分析。计算结果表明,几乎在全桥范围内温度梯度作用下的UHPC层的拉应力值约占汽车荷载作用下的50%。这个比值表明温度梯度对UHPC层拉应力影响较大,故对轻型组合梁的温度梯度效应的研究是不可忽略的。
| [1] | ZUK W. Simplified Design Check of Thermal Stresses in Composite Highway Bridges[J]. Highway Research Record,1965,103:10. |
| [2] | EMANUEL J H, HULSEY J L. Temperature Distributions in Composite Bridges[J]. Journal of Structural Division, 1978, 104(1) :65-78. |
| [3] | KENNEDY J B, SOLIMAN M H. Temperature Distribution in Composite Bridges[J]. |
| [4] | 邵旭东,曹君辉,易笃韬,等.正交异性钢板-薄层RPC组合桥面基本性能研究[J].中国公路学报,2012,25(2):40-45. SHAO Xu-dong, CAO Jun-hui, YI Du-tao,et al. Research on Basic Performance of Composite Bridge Deck System with Orthotropic Steel Deck and Thin RPC Layer[J]. China Journal of Highway and Transport, 2012, 25(2):40-45. |
| [5] | 凯尔别克 F. 太阳辐射对桥梁结构的影响[M]. 北京:中国铁道出版社,1981:1-32. KEHLBECK F. The Influence of Solar Radiation on Bridges Structure [M]. Beijing: China Railway Publishing House, 1981:1-32. |
| [6] | 汪剑.大跨预应力混凝土箱梁桥非荷载效应及预应力损失研究[D].长沙:湖南大学, 2006. WANG Jian. Research of Thermal Effects, Shrinkage and Creep Effects, and Prestress Losses in Long-span PC Box Girder Bridge [D].Changsha: Hunan University, 2006. |
| [7] | 逯彦秋,陈宜言,孙占琦,等.钢桥桥面铺装层的温度场分布特征[J].华南理工大学学报:自然科学版,2009,37(8):116-121,126. LU Yan-qiu, CHEN Yi-yan, SUN Zhan-qi,et al. Characteristics of Temperature Field Distribution of Steel Bridge Deck Pavement[J].Journal of South China University of Technology:Natural Science Edition, 2009,37(8):116-121,126. |
| [8] | MCCLURE R M, WEST H H, HOFFMAN P C. Observations from Tests on a Segmental Bridge[J]. Transportation Research Record, 1984, 950: 60-67. |
| [9] | 彭友松.混凝土桥梁结构日照温度效应理论及应用研究[D].成都:西南交通大学, 2007. PENG You-song. Study on Theory of Solar Radiation Thermal Effects on Concrete Bridges and Its Application [D]. Chengdu: Southwest Jiaotong University, 2007. |
| [10] | KREITH F, KREIDER J F. Principles of Solar Engineering[M].Washington,D.C.: McGraw-hill, 1978. |
| [11] | 陈珊,孙继银,罗晓春.目标表面太阳辐射特性研究[J].红外技术, 2011, 33(3):147-150. CHEN Shan, SUN Ji-yin, LUO Xiao-chun. Research of Target Surface Solar Radiation Characteristic[J].Infrared Technology,2011, 33(3):147-150. |
| [12] | NARUOKA M, HIRAI I, YAMAGUTI T. The Measurement of the Temperature of the Interior of the Reinforced Concrete Slab of the Shigita Bridge and Presumption of Thermal Stresses[C]// Proceedings of the Symposium on the Stress Measurements for Bridges and Structures. Tokyo, Japan : Japanese Society for Promotion of Science, 1957: 109-115. |
| [13] | BERWANGER C, SYMKO Y. Thermal Stresses in Steel-concrete Composite Bridges[J]. |
| [14] | JTG D60—2004,公路桥涵设计通用规范[S]. JTG D60—2004,General Code for Design of Highway Bridges and Culverts [S]. |
 2015, Vol. 31
2015, Vol. 31
