扩展功能
文章信息
- 赵明华, 陈侃, 刘猛, 顾美湘, 孙琮涵
- ZHAO Ming-hua, CHEN Kan, LIU Meng, GU Mei-xiang, SUN Cong-han
- 考虑桩体压缩变形的碎石桩复合地基非线性固结分析
- Analysis of Nonlinear Consolidation of Gravel Pile Composite Foundation Considering Compression Deformation of Pile
- 公路交通科技, 2015, Vol. 31 (6): 46-53
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (6): 46-53
- 10.3969/j.issn.1002-0268.2015.06.008
-
文章历史
- 收稿日期:2014-04-25
碎石桩复合地基作为一种有效的地基处理手段,因其取材方便、施工简单、造价低廉,且具有良好的振密挤密、置换、排水固结和抗液化等作用而在软基处理中广泛应用[1]。碎石桩复合地基的固结理论是土的变形性质及地基沉降计算中非常重要的研究课题。
目前已有大量有关碎石桩复合地基的固结研究,但主要集中在复合地基的线性固结理论。Han J和Ye S L[2]提出了一种简化的固结计算方法,指出碎石桩复合地基中的竖向渗流对平均固结度的影响很小。韩杰等[3]和张爱军等[4]研究了应力集中效应对碎石桩复合地基固结的影响。邢皓枫等[5]将桩间土径向整体作为一个研究对象,用平均超孔隙水压力的概念推导出一种简化的固结计算式。然而,在实际工程中,随着地基土体孔隙水的排出,孔隙比逐渐减小,地基土体将呈现出压缩系数与渗透系数的非线性变化特征。Taylor[6] 提出的土体压缩系数e-lg σ′和渗透系数e-lg k半对数模型在软土工程中应用广泛。针对地基土的非线性固结特性,Lekha等[7]和Indraratna等[8]采用e-lg σ′和e-lg k半对数模型,分别得到了天然地基非线性固结的解析解和砂井地基径向固结的近似解。在假定无井阻的条件下,卢萌盟等[9]通过引入e-lg σ′和e-lg k半对数模型,给出了一种碎石桩复合地基非线性固结的解析解。
以上研究均采用了桩土界面流量相等的假设,然而,在桩土等应变条件下,桩体和土体的变形在任一深度处相同,这与桩土界面流量相等的假设相互矛盾。针对这个矛盾,赵明华等[10]和卢萌盟等[11]分别考虑了桩体的固结变形,即认为桩体排出地基的水量等于土体进入桩体的水量和桩体体积变形量之和,从而避免了桩土界面流量相等和等应变假设的矛盾,推得复合地基的固结方程,但两者均假设压缩模量为常数,与实际情况尚存在较大差别。
综上所述,本文在前人研究基础上,引入土体的e-lg σ′和e-lg k半对数模型,综合考虑井阻作用、扰动作用和应力集中效应,建立出碎石桩复合地基非线性固结微分方程组,推导得到了非线性固结解析解。并通过工程实例和已有解析方法验证了本文方法的合理性和可行性,最后对复合地基的非线性固结性状进行了参数分析。
1 计算模型
在大面积均布堆载P0情况下,以单桩影响范围内的复合地基为分析模型,如图 1所示,坐标原点在桩端中心,只有顶面透水,其他都是不透水界面;考虑扰动作用,土体分为扰动区和未扰动区。图中H为软土层总厚度;rp为碎石桩直径;rs为扰动区半径;re为影响区半径。根据文献[12],2re =1.05L(等边三角形布置),2re = 1.13L(正方形布置),L为桩心距。
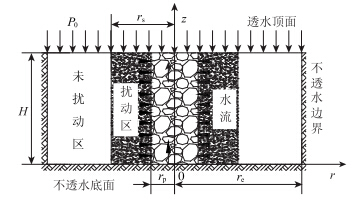
|
| 图 1 碎石桩复合地基固结计算模型 Fig. 1 Calculation model of consolidation of gravel pile composite foundation |
碎石桩复合地基的固结过程和边界条件等十分复杂,为简化计算,作如下假设:
(1)桩和桩周土为均质体,土体是饱和的,固体颗粒和水不可压缩; (2)固结变形为小变形,符合等应变条件; (3)渗流符合Darcy定律,只考虑桩周土的径向渗流和桩的竖向渗流; (4)外荷载一次性施加并保持不变; (5)土体的压缩性和渗透性在固结过程中随有效应力的增大而呈非线性减小,且减小规律符合e-lg σ′和e-lg k半对数模型; (6)在复合地基的固结过程中,桩体和土体会因变形而被挤密,其压缩模量会随着固结而增长,且两者的压缩模量同比例增长,即
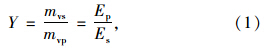
2.2 固结方程推导
根据文献[6],对于常见软黏土都普遍适用的土体压缩系数的e-lg σ′和渗透系数的e-lg k半对数模型的表达式为:

在均布荷载P0作用下,复合地基的竖向平衡方程为:
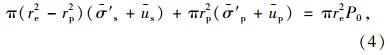
由式(4)可得:
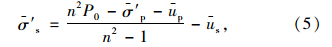
在荷载施加前,地基在初始应力作用下的变形已经完成,故荷载施加后,由等应变假设可得:
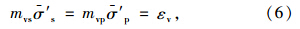
由式(6)可得:
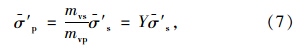
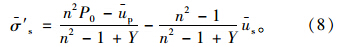
土体内t时刻的平均有效应力为初始有效应力和外部荷载P0在土体内引起的平均有效应力之和,即:
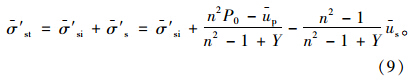
因为外部荷载瞬时施加,则其在复合地基中引起的附加应力与时间无关,故利用式(9)可得:
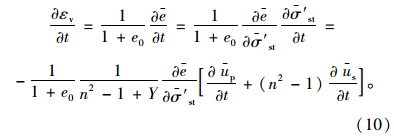
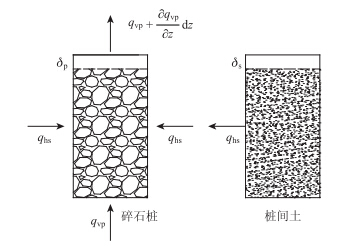
由本文假设可得到z深度处碎石桩和桩间土渗流和变形关系图,如图 2所示。图中qhs,qvp分别为t时间桩周土径向和碎石桩竖向孔隙水流出量。
|
| 图 2 碎石桩和桩间土的渗流和变形关系图 Fig. 2 Relation between seepage and deformation of gravel piles and soil |
dt时间内碎石桩中孔隙水流出量变化ΔQp为:
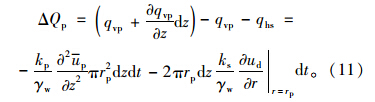
碎石桩体积压缩变化量ΔVp为:
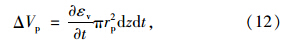
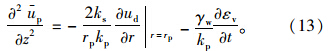
根据饱和土体的体积变化率与水量变化率相等以及达西定律,可得碎石桩复合地基未扰动区和扰动区的固结方程为:
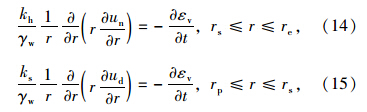
式中un为复合地基未扰动区内的超静孔压。
土中任一深度的平均超静孔压可由式(16)计算:
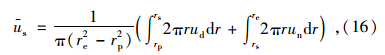
2.3 方程求解
根据计算模型和基本假设可得复合地基固结的边界条件为:
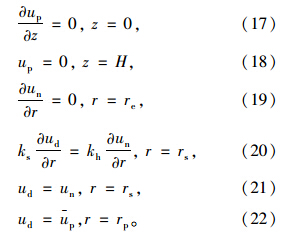
将式(14),(15)两边关于r积分,并应用边界条件式(19)、(20)可得:
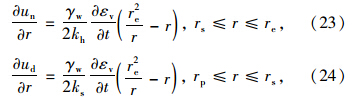
将式(23),(24)关于r积分,并利用边界条件式(21),(22)可得:
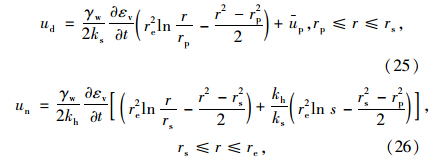
将式(25),(26)代入式(16),可得:
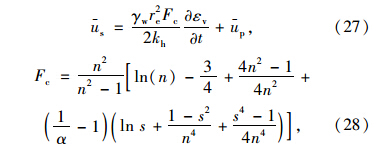
将式(24)代入式(13),可得:
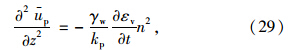
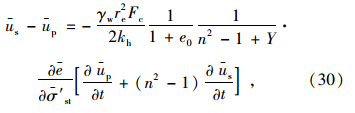
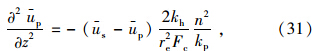
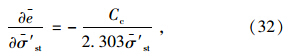
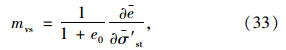
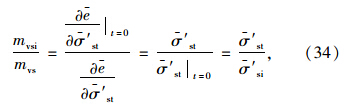
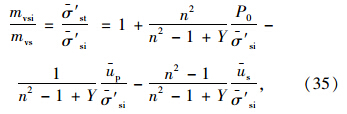
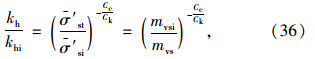
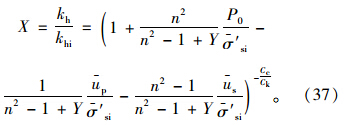
在初始时刻,外部荷载全部由土体内的超静孔压承担,则有:
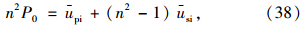
在外部荷载作用下土体内的超静孔压会从初始孔压逐渐消散为零,因此可近似对X取其平均值(即us =0,up=0时和初始孔压时两者之和的1/2),即:
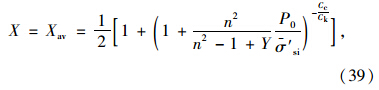
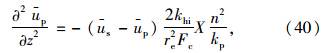
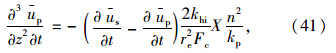
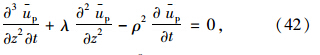
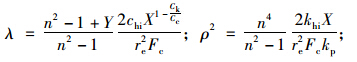
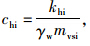 称为土体的初始径向固结系数。
称为土体的初始径向固结系数。 采用分离变量法解方程(42),可得两个独立的常微分方程,即:
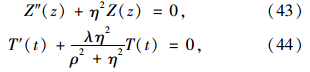
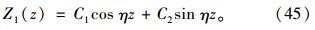
由边界条件式(17)得C2=0;由边界条件式(18)得C1cosηH=0,要使Z1(z)有非零解,且C1≠0,则cosηH=0,即η=M/H必须成立,M=(2m-1)π/2,m=1,2,3…。
式(44)的通解为:

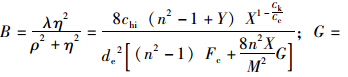
 ,为井阻因子;de=2re,为影响区直径。
于是解得up为:
,为井阻因子;de=2re,为影响区直径。
于是解得up为:
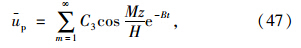
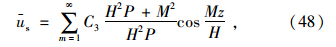
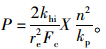
由初始条件ust=o=usi得:
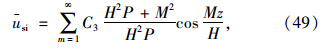
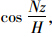 逐次积分可得:
逐次积分可得:
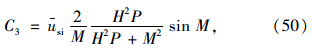
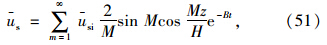
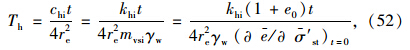
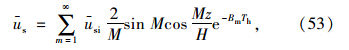
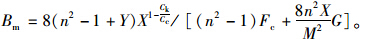
进而可得复合地基任一深度z处的径向平均固结度(按有效应力定义)为:
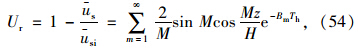
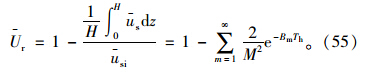
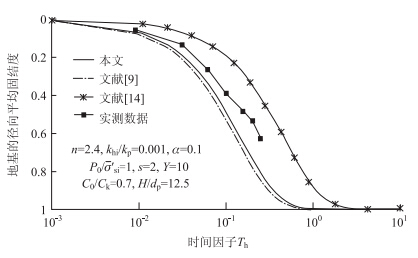
为验证本文方法的合理性和可行性,现以福建某绕城公路工程实例[13]进行验证。该路段软土为淤泥质粉质黏土,平均厚度10 m,含水率37.7%,密度1.86 g/cm3,孔隙比1.03,其他工程性质如表 1所示。桩长10 m,桩径0.8 m,桩心距1.8 m,三角形分布。路面宽度23.5 m,填土高度2.5 m,坡比1∶1.5。
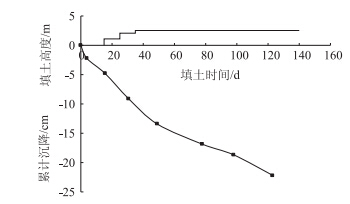
由于在现场进行孔压观测十分困难,为此根据沉降观测数据,利用规范推荐的双曲线方法预测总沉降为34.7 cm,从而可以根据图 3中的数据反推得到地基的固结度。
| 名称 | 初始渗透系数/(m·d-1) | 内摩擦角/(°) | 黏聚力/kPa | 压缩指数 | 渗透指数 |
| 淤泥质粉质黏土 | 1.0×104 | 7.8 | 10.5 | 0.273 | 0.398 |
|
| 图 3 路基中心点沉降曲线图 Fig. 3 Curve of settlement at subgrade center |
在工程中,桩土模量比Y=20,填土荷载P0=γH′=45 kPa(γ为填土重度,取18 kN/m3。填土高度H′=2.5 m),碎石桩处理深度10 m,取深度范围H内土体的平均初始有效应力作为σ′si,计算σ′si所需土体的有效重度γ′=γs-γw=8.6 kPa(γs为地基土的饱和重度,γw为孔隙水重度),平均有效应力σ′si=0.05γ′H=43 kPa,则σ′si,初始体积压缩系数为:
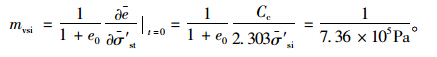
由于复合地基是按三角形布桩,因此单桩的等效处理半径re=1.05L/2=0.95 m,井径比n=re /rp=2.4。土体的初始径向渗透系数与桩体的竖向渗透系数的比值khi/kp=0.001,扰动区半径与桩体半径的比值s=rs/rp=2,扰动区渗透系数与非扰动区初始径向渗透系数比值α=ksi/khi=0.1,压缩指数与渗透指数比值C=Cc/Ck=0.7。
由图 4可以看出,在3种理论计算所得的曲线中本文的计算曲线最接近实测数据,可见本文的计算结果比较符合实际情况,具有较好的合理性和可行性。本文计算结果比工程实测的固结速度要快,这是因为本文采用简单化的计算模型和基本假设以及存在实测误差和计算误差。
|
| 图 4 实测平均固结度与理论计算平均固结度比较 Fig. 4 Comparison between measured value and theoretical value of average consolidation degree |
本文计算曲线位于文献[14]与文献[9]之间,主要原因为:文献[14]提出的是等应变条件下砂井地基的固结计算方法,考虑了井阻作用和涂抹作用,但是没有考虑桩对上部荷载的分担效应,而碎石桩桩复合地基的桩土压缩模量比很大,桩体将承担更大的荷载,出现应力集中现象,土的竖向应力减少会加快超静孔隙水压力的消散,这解释了在加速软土固结速率方面碎石桩为什么比砂井更有效,故本文与文献[9]的计算所得固结速率较文献[14]的要快。文献[9]在计算桩周土径向固结时没有考虑桩体的固结变形,而本文考虑了这一因素的影响,故在相同条件下,本文计算得到的固结速率比文献[9]的要慢;另外本文与文献[9]的方法都考虑了桩和桩周土的荷载分担效应,但卢萌盟等[9]在计算之前假定无井阻作用,即认为桩的排水能力无穷大,而本文考虑了井阻作用,所以本文计算得到的固结速率比文献[9]计算得到的固结速率稍慢,但两者差别不大,这是因为工程实例中的碎石桩渗透系数较大。当碎石桩的渗透系数较小(即碎石级配较好)时,两者的结果差别明显加大,本文计算结果将会更符合实际情况,本文方法更适宜。
4 参数分析
由整个地基的径向平均固结度表达式可知,碎石桩复合地基的平均固结度有很多影响因素,利用matlab程序分析各类影响因素对整个地基的径向平均固结度的影响。
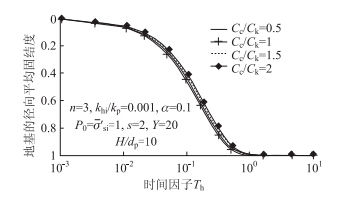
Berry 和Wilkinson[15]的研究表明,Cc/Ck的值一般介于0.5~2.0,分析取用的Cc/Ck值均在此范围内。由图 5可以看出:随着Cc/Ck的增大,碎石桩复合地基固结速率减慢,但变化幅度不大。
|
| 图 5 压缩指数与渗透指数比对固结度的影响 Fig. 5 Effect of ratio of compression index and permeability index on consolidation degree |
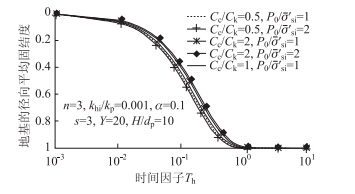
由图 6可以看出,当Cc/Ck<1时,随着均布荷载P0的增大,均布荷载与初始有效应力比P0/σ′si增大,碎石桩复合地基固结速率加快;当Cc /Ck>1时,随着均布荷载P0的增大,均布荷载与初始有效应力比P0/σ′si增大,但碎石桩复合地基的固结速率减慢。
|
| 图 6 均布荷载与初始有效应力比对固结度的影响 Fig. 6 Effect of ratio of uniform load and initial effective stress on consolidation degree |
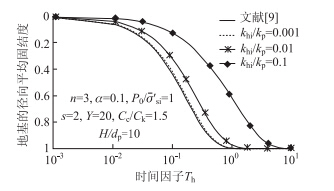
如图 7所示,随着碎石桩渗透系数kp的减小,土的初始径向渗透系数与桩的渗透系数比khi/kp的增大,碎石桩复合地基的固结速率减慢,并且碎石桩渗透系数kp对碎石桩复合地基的固结速率影响比较显著。当碎石桩的渗透系数较小(即碎石级配较好)时,文献[9]计算得到的固结速率比本文计算得到的固结速率快很多,但本文计算得到的固结速率更符合实际情况,所以本文方法更适宜。另外在施工阶段,砂浆中的细颗粒沉淀在碎石桩中导致碎石桩的渗透系数减小,从而减慢碎石桩复合地基的固结速率。因此,在施工中应尽量避免砂浆中细颗粒沉淀在碎石桩中。
|
| 图 7 土的初始径向渗透系数与桩的渗透系数比对固结度的影响 Fig. 7 Effect of ratio of initial radial permeability coefficient of soil and permeability coefficient of pile on consolidation degree |
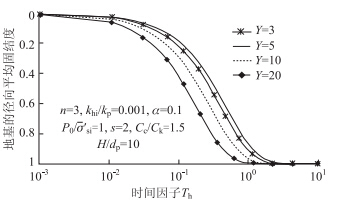
碎石桩复合地基和砂井地基最主要的区别是碎石桩复合地基中桩与土的压缩模量比更高,从而导致应力从土壤向碎石桩集中,即应力集中效应。如图 8所示,本文引入土体的e-lg σ′和e-lg k半对数模型得到了与文献[3]相似的结果,即随着桩与土的压缩模量比Y的减小,碎石桩复合地基的固结速率减慢。
|
| 图 8 桩与土的压缩模量比对固结度的影响 Fig. 8 Effect of ratio of compression moduli of pile and soil on consolidation degree |
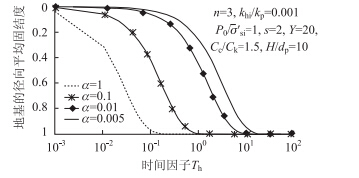
在大多数情况下,因为在扰动区内改变了土的组织结构和破坏了之前良好的排水通道,所以扰动区的渗透系数相对于未扰动区要小。如图 9所示,由于扰动区渗透系数的减小显著减慢了碎石桩复合地基的固结速率。由于扰动区的渗透系数小于未扰动区的渗透系数,随着扰动区半径与桩体半径比s=rs/rp的增大,碎石桩复合地基的固结速率也会减慢,在实际工程中,尽量减少施工扰动区的范围可以提高碎石桩复合地基的固结速率。
|
| 图 9 未扰动区和扰动区内土体的初始径向渗透系数比对固结度的影响 Fig. 9 Effect of ratios of initial radial permeability coefficient of undisturbed and disturbed zones on consolidation degree |
(1)考虑了桩体固结压缩变形和井阻作用等,进一步完善了碎石桩复合地基非线性固结解析理论。本文的碎石桩复合地基固结理论计算结果比文献[14]和文献[9]的计算结果更接近实测值,表明本文方法具有较好的合理性与可行性,且当碎石桩的渗透系数较小(即碎石级配较好)时,本文方法更适宜。
(2)随着Cc /Ck的增大,碎石桩复合地基固结速率越慢,但变化幅度不大。当Cc /Ck<1时,随着均布荷载P0的增大,碎石桩复合地基固结速率加快;当Cc /Ck>1时,随着均布荷载P0的增大,碎石桩复合地基的固结速率减慢。
(3)桩、土压缩模量比的减小和土、桩渗透系数比的增大,均会降低碎石桩复合地基的固结速率,扰动区渗透系数的减小会显著减慢固结速率。
本文的计算模型和假设条件尚存在不足,有些问题需要进一步深入研究,比如:考虑施工荷载、变荷载、循环荷载和地震荷载等复杂荷载下的碎石桩复合地基固结分析。
| [1] | 黄文熙. 土的工程性质[M].北京:中国水利电力出版社,1983. HUANG Wen-xi. Soil Engineering Property[M]. Beijing: China Press Water & Power Press,1983. |
| [2] | HAN J,YE S L. Simplified Method for Consolidation Rate of Stone Column Reinforced Foundations [J]. |
| [3] | HAN J,YE S L. A Theoretical Solution for Consolidation Rates of Stone Column-reinforced Foundations Accounting for Smear and Well Resistance Effects[J]. |
| [4] | 张爱军,谢定义. 复合地基三维数值分析[M]. 北京:科学出版社,2004:49-61. ZHANG Ai-jun,XIE Ding-yi. Three-dimensional Numerical Analysis of Composite Foundation [M]. Beijing:Science Press,2004:49-61. |
| [5] | 邢皓枫,龚晓南,杨晓军.碎石桩复合地基固结简化分析[J].岩土工程学报,2005,27(5):521-524. XING Hao-feng,GONG Xiao-nan,YANG Xiao-jun. Simplified Analysis for Consolidation of Gravel-pile Composite Foundation [J]. Chinese Journal of Geotechnical Engineering,2005,27(5):521-524. |
| [6] | TAYLOR D W. Fundamentals of Soil Mechanics[M]. New York:John Wiley and Sons Inc,1948:700. |
| [7] | LEKHA K R,KRISHNASWAMY N R,BASAK P. Consolidation of Clays for Variable Permeability and Compressibility[J]. |
| [8] | INDRARATNA B,RUJIKIATKAMJORN C,SATHANA-NTHAN I. Radial Consolidation of Clay Using Compressibility Indices and Varying Horizontal Permeability[J]. |
| [9] | 卢萌盟,谢康和,王玉林,等. 碎石桩复合地基非线性固结解析解[J]. 岩土力学,2010,31(6):1833-1840. LU Meng-meng,XIE Kang-he,WANG Yu-lin,et al. Analytical Solution for Nonlinear Consolidation of Stone Column Reinforced Composite Ground [J]. Rock and Soil Mechanics,2010,31(6):1833-1840. |
| [10] | 赵明华,刘敦平,张玲.考虑桩体固结变形的散体材料桩复合地基固结解析计算[J]. 岩土力学,2010,31(2):483-488. ZHAO Ming-hua,LIU Dun-ping,ZHANG Ling. Analytical Solution for Consolidation of Composite Ground with Granular Columns Accounting for Consolidation Deformation of Pile [J]. Rock and Soil Mechanics,2010,31(2):483-488. |
| [11] | 卢萌盟,谢康和,刘干斌,等. 考虑桩体固结和土体渗透性抛物线分布固结解[J]. 岩土工程学报,2009,31(7):1069-1074. LU Meng-meng,XIE Kang-he,LIU Gan-bin,et al. Solutions for Consolidation Considering Column Consolidation and Parabolic Distribution of Soil Permeability [J]. Chinese Journal of Geotechnical Engineering, 2009,31(7):1069-1074. |
| [12] | 曾国熙,龚晓南. 地基处理手册[M]. 2版.北京:中国建筑工业出版社,2000. ZENG Guo-xi,GONG Xiao-nan. Foundation Treatment Manual [M]. 2nd ed. Beijing:China Architecture & Building Press,2000. |
| [13] | 林绍凑. 碎石桩复合地基处理软土固结计算及应用[J]. 福建地质,2012,31(3):273-277. LIN Shao-cou. Consolidation Calculation by Stone Column and of Soft Ground Reinforced Practical Application[J]. Geology of Fujian,2012,31(3):273-277. |
| [14] | 谢康和,曾国熙. 等应变条件下的砂井地基固结解析理论[J]. 岩土工程学报,1989,11(2),3-17. XIE Kang-he,ZENG Guo-xi. Consolidation Theories for Drain Wells under Equal Strain Condition [J]. Chinese Journal of Geotechnical Engineering,1989,11(2):3-17. |
| [15] | BERRY P L,WILKINSON W B. The Radial Consolidation of Clay Soils[J]. |
 2015, Vol. 31
2015, Vol. 31
