扩展功能
文章信息
- 许金良, 鲁娥, 王恒, 李曼
- XU Jin-liang, LU E, WANG Heng, LI Man
- 高速公路弯坡组合路段载重汽车侧滑仿真
- Simulation of Truck Sideslip on Slope-curve Section of Expressway
- 公路交通科技, 2015, Vol. 31 (5): 147-151
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (5): 147-151
- 10.3969/j.issn.1002-0268.2015.05.024
-
文章历史
- 收稿日期:2015-01-19
交通事故是难以避免和预防的小概率事件,但它带来的人员伤亡比任何自然灾害或人为灾害都要大。2009年至2011年,全国发生道路交通事故造成的死亡人数分别是67 759人,65 225人,62 387人。高速公路交通事故中,由载重汽车引起的交通事故数近50%,导致的死亡人数、受伤人数、财产损失比例分别高达60.32%,67.10%,74.22%,严重威胁着高速公路的运营安全。在载重汽车事故中,弯坡组合路段上侧滑引起的撞向固定物是最多的一种单车事故形态。因此,了解侧滑事故发生的诱发因素,可以科学地、有针对性地提出改善措施,对提高高速公路的安全性具有重要意义。
国外学者对汽车侧滑的诱发因素做了大量研究。G. P. Ong等[1]提出了一种基于流体动力学的数值仿真模型来模拟商用卡车的侧滑速度,模型参数包括卡车速度、轮胎载荷、充气压力、路面水膜厚度,结果证明卡车满载时的抗滑性能比空载时差。Gibreel等[2]研究了超高、横向摩擦系数与路面抗滑性能之间的关系。S. M. Easa等[3]提出了一种用没有特定数学形态或遵循最优化模型确定参数的一般二次方程曲线来确定路线超高布置的方法。J. Choi等[4]研究了设计时速140 km/h的智能高速公路最合适的超高与横向摩擦系数值。国内这方面的研究主要包括车辆抗滑性能及侧滑临界条件等方面。王安顺等[5]通过建立转向轮定位参数、车速、荷载、轮胎气压与侧向力的关系模型,分析了侧滑产生的原因及侧向力与侧滑量之间的关系,并建议采用转向轮侧向力指标检测转向轮抗滑性能。郭忠印[6]研究了货车在长下坡与连续弯道组合路段行驶过程中侧滑、侧翻和紧急制动条件下的临界车速,以识别行车危险位置。张德兆等[7]结合道路曲率、驾驶员响应及车辆特征来估计弯道防侧滑最大行驶速度用于限速。
不难发现,上述研究多是针对引起车辆侧滑的因素及其风险程度开展的,研究多受到数据制约,无法确定单个因素的影响力,特别是对汽车侧滑时驾驶员-道路-车辆的响应状态缺乏深入研究。国外研究分析认为,侧滑事故的发生与车辆、基础设施和不良环境的耦合密切相关。因此,仅对一个特定路段或特定区域的历史事故数据的观察分析,很难用于解释单车侧滑事故的发生机理,还需要一个合理的仿真模型,既可用于事故再现,又能在缺少历史事故数据的情况下,合理预测侧滑事故潜在的风险因素。基于此,本文在前期研究的基础上,引入驾驶员操作(包括正常操作和紧急操作)参数,构建完善的道路模型,建立弯坡组合路段侧滑事故发生时的驾驶员-道路-车辆瞬态动力学响应模型。
1 基于ADAMS的驾驶员-道路-车辆瞬态动力学响应模型为了了解汽车转向时的动力学响应机制,通常采用数值模拟的方式对车辆进行仿真计算,以获取车辆运动时的各项参数值[8]。本文采用Adams/Car机械系统动力学自动分析软件,建立侧滑事故发生时的驾驶员-道路-车辆瞬态动力学响应模型。该软件可创建完全参数化的机械系统几何模型,采用多体系统动力学理论建立动力方程,对虚拟机械系统进行静力学、运动学和动力学分析,最后得到位移、速度、加速度和反作用力等曲线[9, 10, 11, 12],供研究分析之用。
1.1 载重汽车仿真模型根据依托工程中的道路工况和载重汽车的组成,选定东风系列大力神车型作为主导车型。该车前桥为1型轴,即单轴单轮;后桥为5型轴,即两侧各有4个轮胎的双联轴,具体参数见表 1。
| 车辆型号 | 东风系列 | 车辆型号 | 东风系列 |
| 整车质量/t | 6.270 | 车身长度/m | 7.7 |
| 额定载重/t | 10 | 车身高度/m | 3.95 |
| 实际载重/t | 10 | 车身宽度/m | 2.49 |
| 最大前刹车扭矩/(N·m) | 16 000 | 转向传动比 | 20 |
| 最大后刹车扭矩/(N·m) | 4 000 | 齿条比率 | 471.0 |
| 前后轮刹车效率比 | 0.65 |
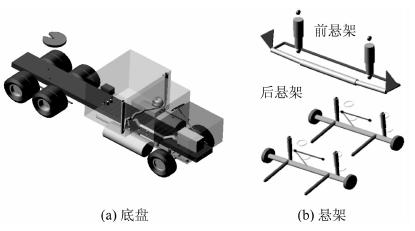
采用基于刚柔耦合效应的载重汽车模型建模。汽车前桥为转向桥,安装有转向横向拉杆、横向稳定杆、减震器、转向梯形臂和转向节三角臂,钢板弹簧采用变截面少片簧。汽车后桥为双驱动桥,每个驱动桥采用单纵臂空气悬架,有利于提高汽车的抗纵倾能力。建模后的汽车模型见图 1。
|
| 图 1 汽车模型 Fig. 1 Truck model |
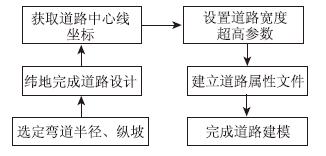
采用3D样条路面来建立非实测弯道路面模型,路面建模流程见图 2。
|
| 图 2 非实测弯道路面建模流程图 Fig. 2 Flowchart of modeling non-measured road pavement |
ADAMS/Car提供开环和闭环2种驾驶员控制方式,本文采用闭环控制。闭环控制考虑驾驶员-道路-车辆之间的反馈调节作用,驾驶员能根据道路与车辆的具体状况及时调节汽车的轨迹、速度等运动状态。仿真载重汽车以道路中线为目标轨迹,通过驾驶员控制文件模拟其紧急制动行为,使载重汽车维持在预定的纵向加速度和初速度附近,在各试验点采取紧急制动措施直至车辆完全停止。
驾驶员控制文件的具体实现过程:以道路中线为目标轨迹,采用纵向加速度控制(lon_accel)和恒速控制(maintain)方式控制汽车初始速度与急刹车后速度,通过Simulate→Full-vehicle Analysis→Event Builde规划建立驾驶员控制文件,以模拟驾驶员的瞬态响应。
1.4 试验点选取在Adams系统中建立12条不同属性的四车道高速公路非实测典型弯坡路面模型,用3条半径分别为600,700,800 m的圆曲线,与4条坡度为2%~5%的纵坡进行组合,初始速度80 km/h。依据理论分析结果和说明问题的需要,选取半径600 m,纵坡为4%,摩擦系数为0.4的下坡左转弯非实测弯坡路段仿真结果进行分析。由于纵、横向附着系数的分配与道路超高和纵坡有很大关系,所以在试验路段上选取10个超高变化点,在各点进行急刹车,模拟测定试验点上各轮胎的纵、横向力的分布。典型试验点见表 2。
| 序号 | 试验点 | 桩号 | 超高/% |
| 1 | 直下坡点 | K0+030 | -0.02 |
| 2 | ZH点 | K0+49.366 | -0.02 |
| 3 | 零坡点 | K0+090 | 0 |
| 4 | 单向超高起点 | K0+130 | 0.02 |
| 5 | HY点 | K0+209.366 | 0.06 |
| 6 | QZ点 | K0+319.048 | 0.06 |
| 7 | YH点 | K0+428.729 | 0.06 |
| 8 | 单向超高终点 | K0+490 | 0.02 |
| 9 | 零坡点 | K0+536 | 0 |
| 10 | HZ点 | K0+588.729 | -0.02 |
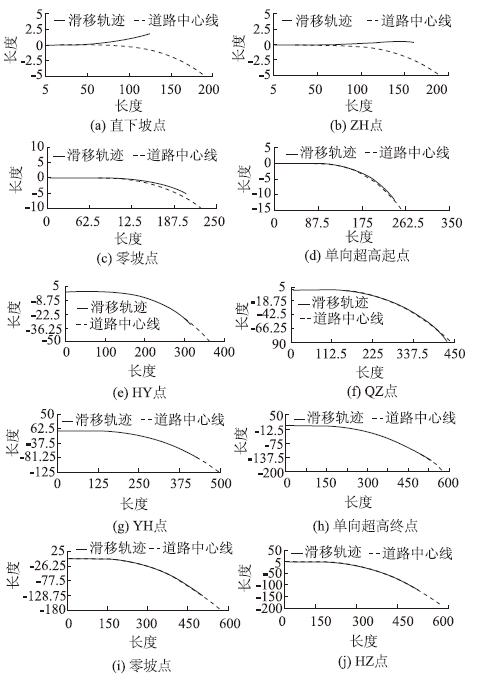
仿真得到的各点的横向滑移轨迹曲线见图 3,虚线即载重汽车的目标轨迹道路中心线,实线轨迹为汽车中心线偏移量,可看作汽车滑移量变化轨迹。
|
| 图 3 弯坡组合路段各试验点仿真车辆横向滑移轨迹 Fig. 3 Tracks of simulating lateral sliding of truck at each measuring point on slope-curve sections(unit:m) |
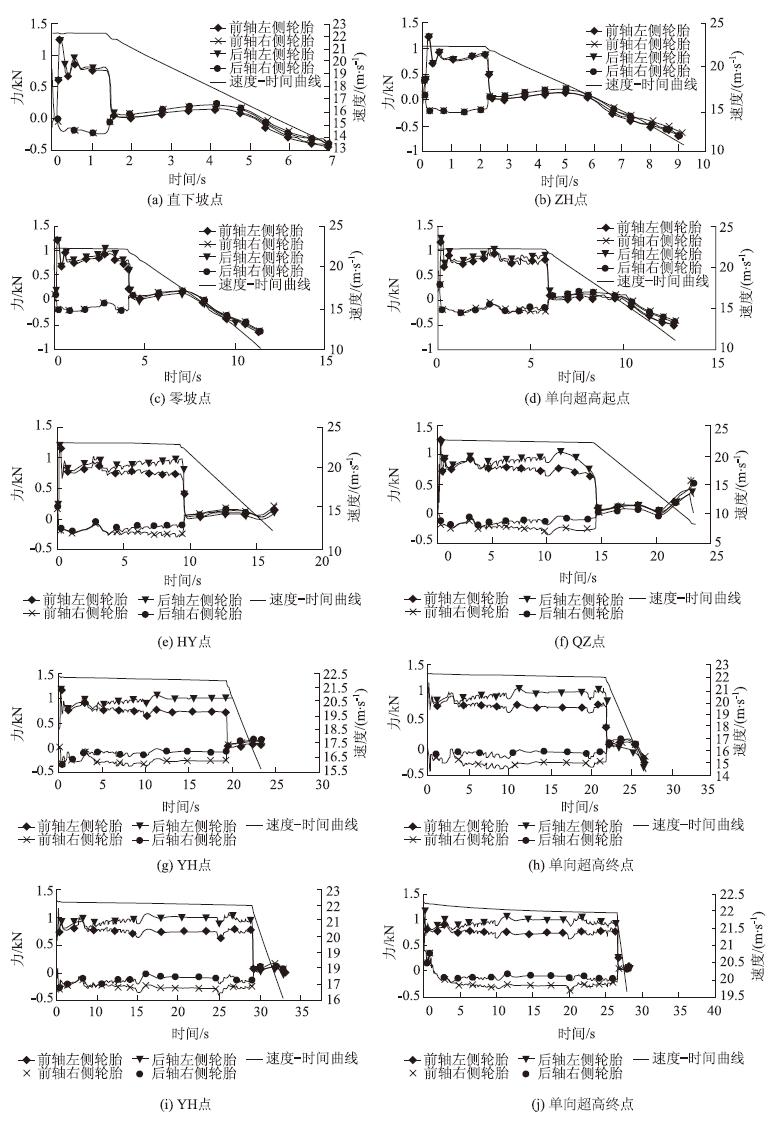
试验得到各点急刹车时汽车后桥前后轴每侧两个轮胎,共8个轮胎各轮的纵、横向力变化图。结果显示各轮的纵向力变化趋势比较一致,急刹车后短暂的剧烈减小后回复到一定水平并稳定,因篇幅限制不做展示。图 4为各试验点各轮横向力的变化,双联轴同轴同侧的内外轮胎受力基本一致。为了展示清晰,说明问题,受力相同的两个轮胎只绘制1条横向力变化趋势线。
|
| 图 4 弯坡组合路段各试验点仿真车辆横向滑移时横向力变化 Fig. 4 Curves of horizontal forces of simulating truck transverse sliding at measuring points on slope-curve sections |
仿真车辆在各试验点的轮胎法向力均一致。此时,纵、横向附着系数之比即纵向力与横向力之比。各试验点即紧急刹车车速突变点,此时纵、横向力随着纵、横附着系数的不断重新分配而变化,通过仿真试验取得的各试验点轮胎纵横向力见表 3。
| 序号 | 试验点 | 超高/% | 纵向力平均值/N | 横向力平均值/N | 纵、横附着系数之比 |
| 1 | 直下坡点 | -0.02 | -5 164.785 3 | 81.564 8 | -63.321 3 |
| 2 | ZH点 | -0.02 | -5 026.589 7 | 79.568 7 | -63.173 0 |
| 3 | 零坡点 | 0 | -4 956.357 8 | 80.567 9 | -61.517 8 |
| 4 | 单向超高起点 | 0.02 | -5 090.909 | 85.602 3 | -59.471 6 |
| 5 | HY点 | 0.06 | -4 656.298 2 | 83.146 7 | -56.001 0 |
| 6 | QZ点 | 0.06 | -4 989.602 5 | 95.265 4 | -52.375 8 |
| 7 | YH点 | 0.06 | -4 825.654 9 | 89.654 9 | -53.824 8 |
| 8 | 单向超高终点 | 0.02 | -5 234.205 6 | 91.245 6 | -57.364 0 |
| 9 | 零坡点 | 0 | -5 123.302 5 | 86.254 6 | -59.397 4 |
| 10 | HZ点 | -0.02 | -4 861.892 5 | 81.567 9 | -59.605 5 |
(1)载重汽车在10个试验点分别进行急刹车操作,汽车速度迅速下降直至为零。滑移轨迹仿真结果显示:载重汽车在直下坡点、ZH点、零坡点、单向超高起点存在侧向滑移,且最大滑移量渐次变小,汽车中线越来越贴近道路中线行驶;载重汽车在后6个试验点的滑移量均很小,接近于零。
(2)从图 4可以看出,紧急制动前汽车后桥双轴左侧轮胎横向力为正,右侧横向力为负(正值方向向左、负值向右),汽车在横向处于稳定状态。紧急制动后,汽车轮胎横向力发生突变,所有轮胎横向力大小及变化趋势几乎一致,对比试验点2和10,3和9,4和8,5和7的横向力变化发现,汽车几乎停止时,横向力仍在负增长的情况下存在侧向滑移,说明汽车横向力缺乏相应的平衡力。直下坡点滑移量最大。
(3)直下坡点只有路拱横坡。ZH点是平曲线段超高从单向路拱超高变化的起点。零坡点是超高从路拱坡度(-2%)向单向路拱超高过渡过程中必须要出现的0超高点。单向超高起点是反向超高的终点,此时的超高为2%。HY点、QZ点及YH点的超高均达到了该试验路段的超高最大值(6%)。单向超高终点是开始出现反超高的地方,此时超高又逐渐减小为2%;第2个零坡点及HZ点的设置与第2个零坡点和ZH点对称。
(4)超高是为了抵消车辆在圆曲线路段上行驶时所产生的离心力而在曲线路段横断面上设置的外侧高于内侧的单向横坡。自第4个试验点开始汽车几乎没有侧向滑移。结合图 4可以看出,超高自此开始发挥维持汽车横向稳定的作用。直下坡点、ZH点、零坡点实际上存在反向超高,载重汽车紧急制动后的横向力没有超高提供的平衡力来抵消,这是汽车横向失稳侧滑的关键原因。
(5)在10个试验点急刹车,8个轮胎的纵向力大小相差不大,变化趋势一致。急刹车后的纵、横向附着系数之比即为路面给轮胎的纵、横向力之比。表 3给出了该比值的具体数值,大小基本都在60左右,并且以QZ点对称。急刹车后横向稳定性不同的原因正是直下坡点至单向超高起点之间存在反向超高。
3 结论(1)载重汽车在弯坡组合路段左转弯下坡方向直下坡点和ZH点处的侧面相撞、撞固定物等事故的多发与反向超高的存在密切相关。反向超高是第1缓和曲线及未设缓和曲线的圆曲线上事故多发的主要原因,且普遍存在。因此,要提高弯坡组合路段的行车安全性,应提前进入超高过渡以避免出现反向超高。
(2)载重汽车在高速公路弯坡组合路段急刹车时,路面附着系数迅速向纵向附着系数转移分配以达到刹车的目的,此时车辆的横向危险性大幅提高。为保证弯坡组合路段行车安全,应避免急刹车并严格限速,警示标志应设立在进入缓和曲线之前。
(3)本文基于Adams仿真试验选取了具有代表性的车型与典型路段进行仿真试验,未来工作中应继续对其他类型典型车辆模型进行扩充和修正,并对不同路段上的车辆侧滑规律进行仿真分析。
| [1] | ONG G P, FWA T F, et al. Modeling Skid Resistance of Commercial Trucks on Highways [J]. |
| [2] | GIBREEL G M, EASA S M, HASSAN Y. State of the Art of Highway Geometric Design Consistency[J]. |
| [3] | EASA S M. Distributing Superelevation to Maximize Highway Design Consistency[J]. |
| [4] | CHOI J, KIM S, JEONG S, et al. Driving Behaviors, the Brainwave Test, and the Distribution of Superelevation and Side Friction Factors for the SMART Highway[C]//ICTIS 2013: Improving Multimodal Transportation Systems-Information, Safety, and Integration. Wuhan: ASCE, 1402-1410. |
| [5] | 王安顺, 张景, 施树明, 等. 汽车转向轮侧滑及其影响因素的研究[J].中国公路学报, 1998, 11(增1):121-137. WANG Anshun, ZHANG Jing, SHI Shuming, et al. Research on the Side Slipping of the Vehicle's Steering Wheel and the Influencing Factors[J]. China Journal of Highway and Transport, 1998, 11(S1):121-137. |
| [6] | 郭忠印, 宋灿灿, 李志勇, 等.长下坡与连续弯组合路段货车行车危险位置识别[J].公路工程, 2012, 37(6):97-108.GUO Zhongying, SONG Cancan, LI Zhiyong, et al. Recognition of Dangerous Sites for Trucks in Long Downgrade and Continuous Curved Combination Road Segments[J].Highway Engineering, 2012, 37(6):97-108. |
| [7] | 张德兆, 王建强, 李升波, 等. 基于风险状态预估的弯道防侧滑超速预警系统[J]. 公路交通科技, 2009, 26(1): 44-48.ZHANG Dezhao, WANG Jianqiang, LI Shengbo, et al. Risk Prediction Based Curve Antisideslip Speed Warning System[J]. Journal of Highway and Transportation Research and Development, 2009, 26(1): 44-48. |
| [8] | TANDEL A, DEHMUKH S, JAGTAP K, et al. Comparison of Multibody Dynamic Analysis of Double Wishbone Suspension Using Simmechanics and FEA Approach[J].International Journal of Research in Engineering and Science, 2014, 2(4):31-37. |
| [9] | CHETAN S J, PRIYAL R P. Parametric Analysis of Four Wheel Vehicle Using Adams/Car [J]. International Journal of Computational Engineering Research, 2013, 2(8):263-268. |
| [10] | SVENDSEN N. Dynamic Analysis of Damping System in FS Car Using ADAMS Multidynamic Simulations[D]. Stavanger: University of Stavanger, 2014. |
| [11] | BOUFOUS S, FINCH C, HAYEN A, et al. The Impact of Environmental, Vehicle and Driver Characteristics on Injury Severity in Older Drivers Hospitalized as a Result of a Traffic Crash [J]. |
| [12] | MUELLER R L. Full Vehicle Dynamics Model of a Formula SAE Racecar Using ADAMS/Car[D]. College Station: Texas A&M University, 2005. |
 2015, Vol. 31
2015, Vol. 31
