扩展功能
文章信息
- 尹春娥, 宋小娜, 刘海朝
- YIN Chun-e, SONG Xiao-na, LIU Hai-chao
- 基于混合粒子滤波的高速公路交通参数自适应估计方法
- A Method of Exporessway Traffic Parameter Self-adaptive Estimation Based on Hybrid Particle Filtering
- 公路交通科技, 2015, Vol. 31 (5): 141-146
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (5): 141-146
- 10.3969/j.issn.1002-0268.2015.05.023
-
文章历史
- 收稿日期:2014-07-11
高速公路交通参数估计是高速公路交通管理与控制的基础工作[1, 2],主要是基于实时的交通监测来估计路网中当前时刻及下一时刻的所有交通参数[3]。早期研究多用基于卡尔曼滤波的方程来进行估计,如扩展卡尔曼滤波(Extended Kalman Filtering,EKF)[4, 5, 6]和无迹卡尔曼滤波(Unscented Kalman Filtering,UKF)[7, 8, 9]。基于卡尔曼滤波参数估计的运算量较小,具有一定的准确性和有效性。但由于交通参数估计实质是一个非线性和非高斯问题,EKF和UKF仍然不能避免随着交通场景的变化呈现出很多不确定性和多样性的误差。而粒子滤波器作为一种可对非线性和非高斯系统直接进行估计的方法,可以有效避免EKF方法的模型线性化问题,近年来逐渐被应用于交通参数估计中[10, 11]。
交通状态估计模型中的参数通常会随交通状态的变化而变化。例如,当估计对象选定为宏观交通流模型时,估计结果对自由流速度、临界密度及相关指数的变化是非常敏感的[12]。在已有研究中,并未考虑到交通状态对估计结果参数的影响,解决方法是将模型中的参数通过离线模型校正采用预设固定参数,致使交通参数估计的准确度受到一定程度的影响[4, 5, 6, 7, 8, 9]。
为达到更高的估计准确度,本文提出一种基于混合粒子滤波(Hybrid Particle Filtering,HPF)的交通参数估计方法,以及交通状态影响下的模型参数自适应调整策略,并通过仿真数据对该方法与策略进行论证分析。
1 参数估计方法研究 1.1 高速公路路段的宏观交通流模型
将高速公路通道分成很多路段,每段长度是Δi,i=1,…,N,时间的离散化是基于时间步T。交通变量有:交通密度ρi(k)、空间平均速度vi(k)、交通流量qi(k)、路段i上的入口匝道流量ri(k)和出口匝道流量。
对于路段i,二阶宏观交通流模型的随机非线性差分方程为:


式(1),式(3),式(4),式(5)分别为经典的密度动态模型、速度动态模型、静态速度方程和交通流方程;τ,v,κ,vf,ρ,ρcr,α,δ为模型参数,所有路段都采用相同的参数值;τ为车速变化比前方Δx处密度变化的滞后时间,也是对驾驶员反应时间的度量;v为速度影响传播速度;κ为常参数,当ρi很小时,该项不至于出现很大、与实际不符的数值;vf为自由流速度;ρcr为临界密度;α为静态速度方程中的指数。ξvi(k)和 ξqi(k)分别为作用在经验速度方程和近似交通流方程上的零均值高斯白噪声,用于反映模型误差;βi(k)为车辆离开率;λi为车道数量。
模型结果对vf,ρcr,α的变化是非常敏感的[3],本文选取这3个参数作为未知模型参数。基于交通量Q(ρ)=ρV(ρ),路段的通行能力(每车道)可以推导为:

将式(2)和式(5)代入式(1)和式(4),最后代入式(3),这样N个路段的通道模型就包含了2N个方程和2N个独立的段变量ρ1,v1,ρ2,v2,…,ρN,vN,3个模型参数vf,ρcr,α以及一系列边界变量:(1) 通道起点的交通流q0;(2) 通道起点的速度v0;(3) 通道终点的密度ρN+1;(3) 入口匝道交通流ri;(4) 出口匝道交通流率βi。
1.2 状态空间模型由N个路段组成的通道模型所包含的全部变量可以包含在向量z,d,p和ξ1中,其中,路段状态向量z由通道中N个路段的密度和速度组成,代表了模型的状态,表示为:

边界向量d由宏观交通流模型的通道边界处的参数组成,代表了模型的外部输入,表示为:

模型参数向量p包含了未知的重要模型参数,代表了模型的一些重要内在特性,表示为:

噪声向量ξ1表示为:

快速通道的宏观交通流模型可以表示为一个紧凑的状态空间形式:

h为非线性可微向量的函数。为克服模型参数造成的误差,将式(11)中的边界变量d(k)和模型参数p(k)转换成如下形式:

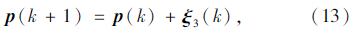
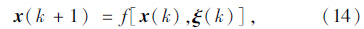
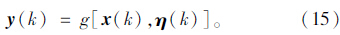
输出向量y包含所有可用于交通流和平均速度的测定;g是一个非线性可微向量的函数;η为输出噪声向量,它可以被视为状态噪声向量ξ和测定噪声向量γ的函数。式(14)和式(15)组成空间模型为:
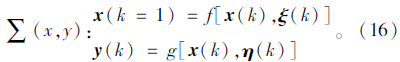
1.3 基于混合粒子滤波HPF的交通参数估计方法
本文所关注的状态空间模型为式(16)。根据贝叶斯理论,后验概率p(x0:k+1|y0:k+1)包含了对状态x0:k+1估计的所有信息。粒子滤波算法通过在重要性分布π(·)采样获得一组离散样本点xi0:nNi=1来近似计算后验概率,并得到粒子的重要性权重:
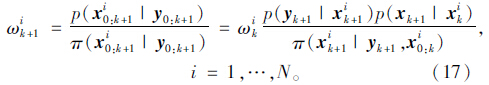
在先验概率分布p(x0)上采样获得粒子,然后通过概率分布:
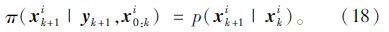
更新粒子并假设状态噪声服从高斯分布,有:

粒子重要性权重为:
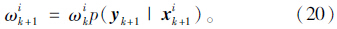
似然函数为:

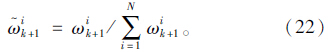
状态xk+1的最小均方估计可表示为:
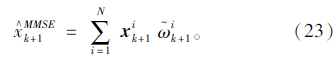
为防止较大观测噪声造成后验概率描述不准而影响性能,考虑对状态xk+1的顺序估计满足:
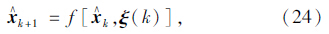

考虑卡尔曼滤波得到最优估计x∧k+1,有:
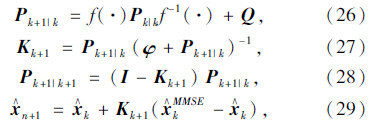
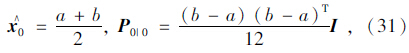
由宏观交通流模型可知,参数估计结果对自由流速度、临界密度和指数的变化是非常敏感的。由于临界密度与指数是相对固定且不随交通运行条件改变的,而自由流速度则容易受到道路条件如车道数、平曲线半径、进出口匝道距离及交通运行条件如饱和度(V/C)的影响。因此,考虑将自由流速度作为未知的模型参数,其他模型参数都由离线模型校正来决定。在仿真试验分析中,将会根据具体数据给出自由流速度与交通饱和度之间的函数关系,以期基于交通状态自适应变化的自由流实测速度取代预设固定的自由流速度,通过自由流速度的自适应调整,达到更高的估计准确度。
1.5 性能评价指标选用绝对和相对性能指标来评估参数轨迹性能[12],绝对性能指标为:
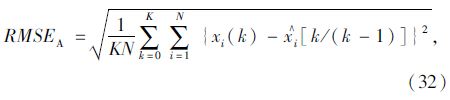
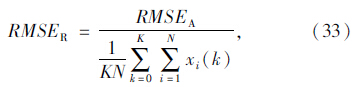
2 仿真试验
为了检验所提出模型的估计效果,对高速公路交通参数估计进行仿真分析,对路段上的速度及交通量进行估计。仿真方案分为正常和发生事故两种情况。仿真在Matlab环境下进行,对于每种情况,分别采用EKF,UKF,HPF进行交通参数估计并比较性能;然后,再将自适应调整策略应用到EKF,UKF和HPF中,进行综合比较分析。
2.1 仿真环境介绍仿真公路如图 1所示。仿真实例选择1条5.6 km长的高速公路,将该路平均分成7个路段,编号为1,2,…,7, 在5号路段开设有进口匝道。假设该路段上有3个交通检测器,分别为D1,D2,D3,被分别安装在路段入口、出口以及第5号路段与第6号路段的交界处。仿真时间跨度设置为8 h,时间为12:00—20: 00。仿真入口的交通量曲线和速度曲线分别如图 2和图 3所示。状态向量定义如下:


|
| 图 1 仿真路段道路结构与交通检测器配置 Fig. 1Structure of simulation section and configuration of traffic detectors |

|
| 图 2 仿真路段入口交通流量 Fig. 2Traffic flows of simulation section entrance |

|
| 图 3 仿真路段入口速度曲线 Fig. 3Velocity curve of simulation section entrance |
参数设计如下:τ=20 s,v=35 km2/h,δ=1.4,κ=13 veh/(km·lane),vf=120 km/h,ρcr=40 veh/km,α=2。状态每10 s更新1次,而观测数据每60 s到达1次。仿真过程中所有的噪声都假设为零均值的高斯白噪声。基于经验选定标准差,粒子数量N=300,其他标准差取值如下: D[ξq1(k)]=100 veh/h,D[ξv1(k)]=10 km/h, D[ξq0(k)]=100 veh/h,D[ξv0(k)]=4.5 km/h。 2.2 自由流速度随交通状态的自适应变化
通过记录仿真过程中实测自由流速度与饱和度的数据,计算得到仿真过程中速度与饱和度之间的关系如图 4所示,建立回归模型如式(35)所示。最大绝对误差值为5.91 km/h,最大相对误差为6.25%,误差较小,可以用于试验分析。
自由流速度为:


|
| 图 4 仿真条件下自由流速度观测值与交通饱和度曲线关系图 Fig. 4Observed free flow speeds and curves of traffic saturation under simulation condition |
图 5显示了正常情况下利用EKF,UKF,HPF进行交通参数(交通量和速度)估计的情况。对比发现,PHF的估计曲线和实际情况拟合程度高于EKF和UKF,能够迅速地识别交通量和速度较明显的波动。当采用了参数自适应调整后,交通量和速度估计曲线与实际情况的拟合程度明显好于无参数自适应调整的情况。从表 1可以进一步看出,参数自适应调整能较明显地提高估计准确度,而且HPF的性能要明显高于EKF和UKF。

|
| 图 5 正常情况下基于仿真数据的交通参数估计 Fig. 5Estimation of traffic parameters based on simulation data under normal condition |
| 参数 | 交通量 | 速度 | ||||||
|
参数自适 应调整 | 无调整 | 调整后 | 无调整 | 调整后 | ||||
| 性能 指标 | RMSEa |
RMSEr/ % | RMSEa |
RMSEr/ % | RMSEa |
RMSEr/ % | RMSEa |
RMSEr/ % |
| EKF | 3.408 | 25.67 | 3.126 | 22.34 | 14.365 | 18.21 | 12.704 | 15.80 |
| UKF | 2.113 | 17.53 | 1.983 | 14.92 | 11.282 | 14.26 | 9.391 | 12.12 |
| HPF | 1.347 | 13.82 | 1.109 | 11.30 | 7.653 | 9.38 | 5.908 | 7.87 |
假设在13:00整检测器D2处发生了交通事故,占用了1条车道,事故持续了30 min,在13:30结束。在图 6中显示了发生事故情况下采用EKF,UKF,HPF进行交通参数估的计的情况。可以发现,采用HPF进行交通参数的估计曲线和实际曲线

|
| 图 6 事故情况下基于仿真数据的交通参数估计 Fig. 6Estimation of traffic parameters based on simulation data under accident condition |
事故情况下3种方法的性能对比如表 2所示,表中情况更加印证了上述曲线的分析结果。但由于受到交通事故的影响,交通参数在事故发生时段波动过大,使得表 2中的估计准度相比于表 1所示的正常情况略有下降。
| 参数 | 交通量 | 速度 | ||||||
|
参数自适 应调整 | 无调整 | 调整后 | 无调整 | 调整后 | ||||
| 性能 指标 | RMSEa |
RMSEr/ % | RMSEa |
RMSEr/ % | RMSEa |
RMSEr/ % | RMSEa |
RMSEr/ % |
| EKF | 3.624 | 28.64 | 3.543 | 25.73 | 17.362 | 20.31 | 15.005 | 19.02 |
| UKF | 2.432 | 19.32 | 2.126 | 17.21 | 13.781 | 17.92 | 12.261 | 15.37 |
| HPF | 1.653 | 14.98 | 1.305 | 14.01 | 9.015 | 12.17 | 8.322 | 10.12 |
(1)基于混合粒子滤波的交通参数估计准确度明显高于卡尔曼滤波估计。在正常情况下和事故运行场景下,都能快速识别交通量和速度的较明显波动,说明基于混合粒子滤波的参数估计在应对交通场景的变化时表现出了更强的稳定性。
(2)交通状态影响下的模型参数自适应调整策略对交通参数估计准确度具有显著影响。采用参数自适应调整后的估计效果明显好于无参数自适应调整的情况,即使在发生事故导致交通流异常波动的情况下,尽管准确度有所下降,但也达到了较好的估计效果。
(3)当事故发生时,估计准确度会略有下降,说明估计准确度对异常交通参数波动较为敏感。在下一步的研究中,将深入分析事故持续时间和影响范围对估计准确度的影响。
| [1] | HERRERA J C, BAYEN A M. Incorporation of Lagrangian Measurements in Freeway Traffic State Estimation [J]. |
| [2] | VAN LINT J W C, HOOGENDOORN S P. A Robust and Efficient Method for Fusing Heterogeneous Data from Traffic Sensors on Freeways[J]. |
| [3] | WANG Y, PAPAGEORGIOU M, MESSMER A, et al. An Adaptive Freeway Traffic State Estimator[J]. |
| [4] | WANG Y, PAPAGEORGIOU M, MESSMER A. RENAISSANCE: A Unified Macroscopic Model-based Approach to Real-time Freeway Network Traffic Surveillance[J]. |
| [5] | WANG Y, PAPAGEORGIOU M, MESSMER A. Real-time Freeway Traffic State Estimation Based on Extended Kalman Filter: A Case Sudy[J]. |
| [6] | 董春娇, 邵春福, 周雪梅, 等. 基于交通流参数相关的阻塞流短时预测卡尔曼滤波算法[J]. 东南大学学报: 自然科学版, 2014, 44(2): 413-419. DONG Chun-jiao, SHAO Chun-fu, ZHOU Xue-mei, et al. Kalman Filter Algorithm for Short-term Jam Trafic Prediction Based on Traffic Parameter Correlation[J]. Journal of Southeast University: Natural Science Edition, 2014, 44(2): 413-419. |
| [7] | ROMANENKO A, CASTRO J A A M. The Unscented Filter as an Alternative to the EKF for Nonlinear State Estimation: A Simulation Case Study[J]. |
| [8] | YE Z, ZHANG Y, MIDDLETON D R. Unscented Kalman Filter Method for Speed Estimation Using Single Loop Detector Data[J]. Transportation Research Record, 2006, 1968(1): 117-125. |
| [9] | 程松, 陈光梦. 一种利用UKF的高速公路实时交通状态估计方法[J]. 计算机工程与应用, 2008, 44(8):226- 229. CHENG Song, CHEN Guang-meng. Real-time Motorway Traffic State Estimation Based on Unscented Kalman Filtering[J].Computer Engineering and Applications, 2008, 44(8): 226-229. |
| [10] | MIHAYLOVA L, BOEL R, HEGYI A. Freeway Traffic Estimation within Particle Filtering Framework[J]. |
| [11] | MIHAYLOVA L, HEGYI A, GNING A, et al. Parallelized Particle and Gaussian Sum Particle Filters for Large-scale Freeway Traffic Systems[J]. |
| [12] | WANG Y, PAPAGEORGIOU M. Real-time Freeway Traffic State Estimation Based on Extended Kalman Filter: a General Approach[J]. |
 2015, Vol. 31
2015, Vol. 31
