扩展功能
文章信息
- 王凯旋, 苏永华, 张盼凤, 罗正东
- WANG Kai-xuan, SU Yong-hua, ZHANG Pan-feng, LUO Zheng-dong
- 基于改进RMR方法的深部隧道稳定性分析
- Analysis on Stability of Deep Tunnel Based on Modified RMR Method
- 公路交通科技, 2015, Vol. 31 (5): 123-128
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (5): 123-128
- 10.3969/j.issn.1002-0268.2015.05.020
-
文章历史
- 收稿日期:2014-06-18
2. 湘潭大学 土木工程与力学学院, 湖南 湘潭 411105
2. School of Civil Engineering and Mechanics, Xiangtan University, Xiangtan Hunan 411105, China
荷载-结构法因其概念清晰,方法简单,易于接受掌握等特点而成为地下结构工程中广泛应用的计算模型[1]。该方法的关键在于准确确定支护结构上的作用荷载,以保障后续支护结构设计的安全可靠,科学合理。目前该计算模型中荷载的确定方法有多种,如卡柯公式法、普氏理论法及规范法等,且随着研究的发展又有一些新的方法被提出来。之前有学者[2, 3, 4]基于工程界广泛采用的RMR分类方法提出围岩顶板压力确定方法,将其系统评分RMR值作为顶板压力确定公式中的重要参数。该法利用地质勘察资料,基于RMR分类方法获得RMR值进而直接确定作用荷载,简单且易于操作,但分析结果往往不太理想[5]。鉴于此,本文从RMR分类方法本身着手对其原因进行探究。
RMR地质分类方法是由Bieniawsk于1973年提出,后经多次修改,目前的版本共考虑6个方面因素的影响。其中由Deer提出的RQD表示大于等于10 cm的岩芯累积长度占整个钻孔进尺长度的百分率,是RMR分类方法依赖的重要评价参数之一,主要体现的是岩芯的完整程度,是表征岩体结构的指标之一。但是,之后的研究[6]发现RQD本身存在不足之处:以10 cm作为分界没有给出充分论证,所有尺寸大于10 cm的岩块在评价岩芯质量的过程中被认为作用相同,而所有尺寸小于10 cm的岩块在评价岩芯质量时又不考虑在内。这些不足导致在某些情况下RQD值显得意义不大,并不能很好地反应岩芯质量。因此,有必要改进岩芯质量评价方法,使其能够满足RMR系统分析结果准确性的要求。
另外,大量的研究[7, 8]表明,在地下工程施工期间进行的岩体开挖,由于地应力的原因常常会促使开挖影响范围内的岩体产生一系列的变形和破坏现象,使该区域岩体质量发生改变,甚至导致工程岩体失稳,并且地应力越大,影响越大。所以,在对深部隧道工程的岩体质量进行评估时,其地应力的影响应当考虑在内,且不可忽略。但是在RMR分类方法中,地应力作为与岩体稳定性和工程运营可靠性密切相关的影响因素并没有被充分考虑到。
鉴于上述原因,本文将引入更准确表征岩体质量的岩体块度指数,并考虑地应力影响,对RMR分类方法进行优化改进。基于改进的RMR值确定支护结构顶板压力,进而与隧道支护体系承载能力联合分析,综合判断隧道的稳定性,形成一个完整的隧道稳定性分析方法。
1 RMR分类方法的改进 1.1 RMR分类方法
RMR分类方法最新的为1989年版本,考虑了6个参数。其中前5项,分别为岩体材料单轴压缩强度,岩芯质量指标(RQD),不连续面间距,不连续面条件以及地下水条件。根据实测资料,按照评分方法,分别给予评分:RMR1,RMR2,RMR3,RMR4,RMR5。将以上各类参数的评分值相加得到岩体质量总分RMRbasic,可表示如下:
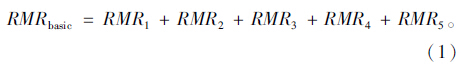
另外,通过地质资料分析,根据节理走向和倾角对岩体是否有利,给予不同的修正值RMR6。所以,最终得到的RMR值可表示如下:
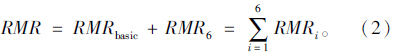
该分类方法自提出之后,引起了学者们的关注,有些研究甚至是在该方法基础上开展的。但是该方法主要是以浅部岩体为研究对象,随着深部工程,复杂环境工程的不断出现,地应力对岩体的影响程度与浅部有所区别。所以分类研究也应该不断的拓展加深,使之适应工程需要。
1.2 岩体块度指数
岩体块度指数RBI是以岩体各基本块度的概率分布为基础,表征岩体完整程度的综合指标。传统分类方法中RQD将大于等于10 cm作为一个尺寸区间对岩块进行统计,不注重块体尺寸的影响。例如:2个岩芯质量指标RQD值均为90,一个岩芯的统计尺寸主要以20~30 cm为主分布,另外一个则以50~60 cm为主,统计分析得到的RQD虽然是一样的,但二者之间的岩体质量显然是有差异的。RMR值对RQD具有相当强的依赖性,可这种差异在RMR分类方法评价过程中却又无法得到体现,使得RQD本身的不足也直接影响着RMR分类方法的评价结果的合理性。针对不足,许多学者提出了改进方法。
长江水利委员会陈德基[9]认为影响岩体工程地质性质的基本因素为岩块的大小,组合比例和裂隙的性状,并于1979年率先提出块度模数的概念,考虑岩体中不同尺寸的岩块并进行统计,加权处理得到块度模数,藉此对岩体的完整性进行评价。刘克远等在“高坝坝基岩体稳定性评价及可利用岩体质量标准的研究”中建立了反映岩体完整程度的岩体块度指数新指标。张世殊[10]对金沙江下游溪洛渡水电站坝基的勘探资料进行分析,以3,10,20,30,50,100 cm作为块度尺寸分级界限,统计获得各区间内岩芯分布概率,同样进行加权处理得到块度指数RBI。胡卸文等[11]在前人研究的基础上再次进行改进,与《水利水电工程地质勘察规范》中评价岩体完整程度时所划分的尺寸保持一致,将实测岩芯长度按3~10 cm,10~30 cm,30~50 cm,50~100 cm和> 100 cm划分,以各块度尺寸区间的岩芯获得率与各自相应系数的乘积之和定义为岩体块度指数RBI值。
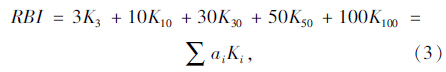
式中,Ki分别为相应的岩芯长度区间的岩芯获得率;ai为相对应尺寸区间的系数。同时发现,在RQD<90%时,岩体块度指数RBI和岩芯质量指标RQD值有较好的对应关系,其关系式如下:
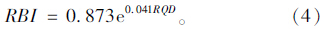
根据现场资料对照RBI值,对岩体质量进行分级,分级情况见表 1。
| 岩体结构 |
整体块状 (Ⅰ级) | 块状 (Ⅱ级) |
次块状 (Ⅲ级) |
镶嵌碎裂 (Ⅳ级) | 碎裂 (Ⅴ级) |
| RBI值 | 100~50 | 50~30 | 30~10 | 10~3 | 3~1 |
苏永华[12]在定量确定公路隧道Hoek-Brown指标的分析过程中,引入文献[10]的RBI分级模式,取得了比较好的效果。 1.3 地应力修正
传统的RMR分类方法主要针对的是浅部岩层,地应力影响程度较小,忽略地应力的影响对工程设计分析影响亦不大。但是对处于大埋深、高应力区域的工程,地应力作为诱导产生破坏的主要原因之一,必须予以考虑。事实上,Q分类、国标《工程岩体分级标准》、隧道围岩分类等方法均考虑了地应力的影响。因此,有必要将地应力的影响考虑在内,对分类方法的RMR值进行修正。
刘业科等[13]针对地下深部工程的三高状况,提出了针对RMR分类方法的地应力修正方法。根据室内岩石强度σc与最大主应力σ1的比值a,将地应力等级分为低应力,中等应力,高应力,极高应力4个等级,并提出地应力修正值w与比值a之间存在以下关系:
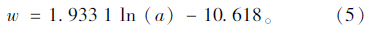
而刘焕新等[14]则参考我国地下洞室岩体分类《工程岩体分级标准》中对地应力的修正方法,考虑岩石抗压强度与最大水平主应力,定义岩体抗压强度σci与最大水平主应力的比值σhmax为损伤系数Z。

然后将损伤系数Z与评分值联系起来,提出损伤系数Z与其评分值的关系式,即Z与地应力修正值W之间的关系式:

由以上分析可知:2种地应力修正关系式虽然都呈现连续性,但是第2种方法地应力修正值与埋深却呈线性关系。根据现场实测数据分析发现,浅埋深的地应力大体呈线性增加,但是当埋深较大时,地应力与埋深的关系并非如此。相较而言,第1种修正方法考虑了深部工程的三高状况,修正方法更为合理,故本文将采用该法对RMR值进行地应力修正。参考RMR分类方法中节理走向和倾角的修正方法,将地应力修正值与前6项相加进行修正,修正值记为RMR7。
1.4 改进后的RMR方法
由前面介绍可以看出岩体块度指数RBI比RQD更能准确反映岩体的完整程度,体现岩体的质量。故在分类方法评分时,将RQD值替换为RBI值对岩体进行质量分级。改进后的RMR分类方法操作过程:对岩芯的块体尺寸进行统计,统计获得岩体块度指数RBI,对照表 1中的分级标准,对岩体质量分级;替换原参数RQD的评价项,依照RMR分类方法获得评分值,即确定RMR2;同样根据1.3章节所述的方法,利用公式(5)确定地应力修正值RMR7。故根据改进后的RMR分类方法,可得到改进后的RMRnew,表示如下:
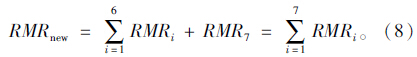
2 支护结构稳定性系数计算 2.1 隧道顶板压力确定
自RMR分类方法提出之后,在许多工程方面得到应用。但随着研究的拓展,有学者提出计算公式,将RMR值作为参数,用于确定隧道工程的支护体系顶板压力。
1983年,Unal[2]以煤层压力的研究成果为基础,引入RMR分类方法,考虑隧道跨度B和隧道岩体重度γ,提出了基于评价结果RMR值的地下工程支护结构顶板压力的确定公式:
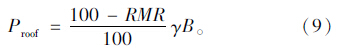
1991年,印度学者Goel,Jethwa[3]同样基于RMR分类方法,考虑隧道埋深H和隧道跨度B,进而提出顶板压力的计算方法:
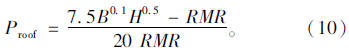
1994年,Goel[4]在他的博士论文里,对25条跨度为2~14 m的隧道进行分析,基于RMR分类方法,考虑隧道埋深H和隧道跨度B,按土层是否挤压,分别提出相对应的隧道支护结构顶板压力确定方法。
(1)对非挤压状态
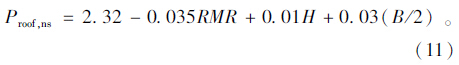
(2)对挤压状态
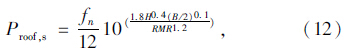
式中,fn是根据地层挤压程度,通过文献[5]中所述方法确定的隧道挤压校正参数。
本文在对RMR值获取方法进行改进及修正的基础上(修正后的值表述为RMRnew),再借鉴前述方法确定隧道支护结构的顶板压力。
2.2 支护体系承载力
现代支护结构一般采用钢筋混凝土,锚杆,钢拱架等支护方式中的1种或者几种。按照P.P. Oreste [15]的观点,如果复合支护结构的应变为线弹性,那么复合支护体系的整体刚度就等于支护体系中各单元支护结构刚度之和,即:

假设各支护单元支护时间相同,弹性变形位移相同,那么支护结构上承担的极限荷载Pmax就等于围岩产生的最大允许位移umax与复合支护体系刚度kcom的乘积,即:

2.3 隧道结构稳定性计算
2.3.1 稳定性分析
根据稳定性定义,结构稳定性可以通过支护抗力与作用荷载比值判定。该方法简单明了,被广泛用于在边坡,地上结构等领域的稳定性分析。
参考其他工程领域的稳定性分析方法,根据地下结构力学地层围岩与支护结构变形协调原理,采用荷载-结构模型对隧道支护结构稳定性进行分析。对本文而言,稳定性系数即为隧道支护结构极限荷载力Pmax与隧道支护结构上作用的顶板压力Proof之比:

(1)基于改进的RMR分类方法,分析获得RMRnew。
(2)利用RMRnew,通过已有顶板压力公式,确定支护结构顶板压力Proof。
(3)分析确定隧道支护结构极限承载能力Pmax。根据一般稳定性原理,计算得到隧道结构稳定性系数Fs。
从以上整个分析过程可以看出,该方法思路清晰,简单易用。特别是对处于一线的地质工作者、工程人员来说易掌握。
3 工程实例分析 3.1 工程概况
湖南湘西某山岭隧道全长3 245 m,开挖断面为马蹄形,开挖高度为8.6 m,最大跨度为11.6 m。按照岩性和地形地貌将隧道分为若干个支护研究段,本文以其中1个分段为例,说明上述方法的应用。
该隧道在勘察阶段设了3个钻井,其中的二号钻孔位置处于该研究段内,钻孔深度为115.20 m,具体钻孔信息见图 1。
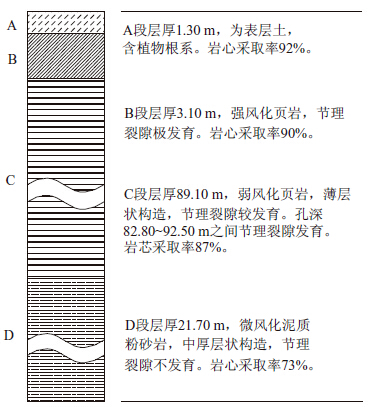
|
| 图 1 二号钻孔柱状图 Fig. 1Histogram of drill hole No.2 |
根据地质勘查结果,对该段的岩芯中属于不同尺寸区间的岩块进行统计,钻孔中各尺寸区间岩芯长度分布统计结果见表 2。
| 区间/cm | 3~10 | 10~30 | 30~50 | 50~100 | >100 |
| 百分比/% | 17.3 | 30.6 | 29.8 | 18.8 | 6.7 |
根据表 2中的统计数据可得该隧道单元段的岩芯质量指标RQD=85.9。
根据表 2数据,按照公式(3)计算得到岩体块度指数RBI=28.619。
依照文献[11]研究结果,利用式(4)计算RBI得:
RBI=0.873e0.041*85.9=29.55。
按照式(3)、(4)计算得到的RBI值相对误差为3.25%,说明当RQD<90%时RQD值与RBI值之间确实存在较好的对应关系。
根据改进前的RMR分类方法对该单元段内的岩体进行评价得到RMR值为50。其中依据RQD确定岩体质量为Ⅱ级,相对应RMR分类方法中评分值RMR2(1)为17;而依据RBI值确定的岩体质量则为Ⅲ级,相对应RMR分类方法中评分值RMR2(2)为13,二者之间评分值差值t=-4。
根据现场勘察及室内试验可以得到:该隧道单元段的岩体重度γ=26.8 kN/m3,岩体抗压强度σc= 27.20 MPa,最大主应力σ1= 5.04 MPa。所以室内岩石强度σc与最大主应力σ1的比值a等于5.396 8,将其代入公式(5)可得相对应的地应力修正值w=-7.34,即RMR7=-7.34。
综合以上分析结果,整理列于表 3。
| RQD | RBI | RMR | t | w | RMRnew |
| 85.9 | 28.619 | 50 | -4 | -7.34 | 38.66 |
对于该单元段,隧道单元段采用的是喷射混凝土和锚杆共同作用的复合支护结构。系统锚杆的平均间距为2.0 m,沿隧道轴向间距为1 m,平均长度为3.0 m,挂金属网,喷射混凝土厚度5 cm。
锚杆的刚度kbolt=9.28410 MPa/m,喷射混凝土的刚度kshot=48.422 62 MPa/m,所以复合支护结构的联合刚度kcom=57.706 72 MPa/m。另外,支护结构允许极限位移ulim=4.003 mm,所以联合刚度与极限位移相乘得到极限承载力Pmax=0.231 MPa。
3.2 计算及比较
利用上述参数,根据改进前、后的RMR分类方法分别确定RMR,RMRnew,结合其他隧道参数,按照式(9)~(12),确定隧道单元段支护结构顶板压力。同一单元段隧道的支护方式相同,支护体系的极限承载能力相同。因此,此处隧道单元段的稳定性由顶板压力确定方法决定。按照2.3.2节所示分析步骤确定单元段隧道稳定性系数,见表 4。
3.3 结果分析
由表 4可以看出,基于改进前后的RMR分类方法,计算得到的稳定性系数有明显差距。
基于改进前分类方法评分值RMR,利用公式(10)、(12)获得隧道单元段支护结构顶板压力,求得该隧道单元段的稳定性系数分别为1.322>1,1.178>1;而基于改进后分类方法评分值RMRnew,采用与上述同样分析方法得到的该隧道单元段稳定性系数分别为0.960<1,0.964<1。
实际情况是该段隧道在建成不久后即出现环向裂纹,混凝土衬砌上的裂纹在不断出现和发展,最后显现宏观裂缝。运营3个月左右,混凝土衬砌结构多处裂纹扩展成断裂(如图 2所示),出现多条沿隧道轴向长达200 m的连续裂缝,支护结构基本被破坏。

|
| 图 2 隧道支护体系断裂破坏 Fig. 2Fracture failure of tunnel support system |
基于改进前方法的分析结果显示该隧道单元段的支护体系设计性能可以满足上部荷载要求;基于改进后RMR分类方法,由于考虑岩体块体尺寸和地应力的影响,分析结果显示该段隧道支护结构无法满足上部荷载要求,这与工程实际情况相符,也证明了改进方法的实用性。
另外,由该隧道后期观测数据发现,上覆岩层超过250 m的隧道段,其支护结构基本都发生破坏,衬砌裂缝明显,说明隧道支护结构承担的荷载大小与埋深有相当大的关系。而公式(9)在计算荷载时却并没有将这一因素考虑在内,使得依据该荷载计算获得的稳定性系数显示,支护结构承载能力仍能满足顶板压力的作用。
综合分析可以得出,岩体块度的尺寸和地应力对工程岩体的质量具有较大的影响。另外,隧道所经区域的岩体质量,隧道的埋深、跨度等是决定支护结构顶板压力的主要因素。
4 结论
本文主要取得了如下几方面的成果:
(1)岩体块度指数RBI是表征岩体块度的综合指标,将其引入到RMR分类方法当中,能更好地反映岩块尺寸对岩体质量的影响。
(2)考虑地应力影响,对RMR评分值进行了修正,分析结果表明地应力对岩体的稳定性有较大影响。
(3)构建了基于荷载-结构模型的隧道支护结构整体稳定性系数计算框架。并结合工程实例,通过对比分析发现基于改进RMR分类法的分析结果更符合实际工程状况。
(4)岩体风化、软化等诸多不确定性因素对RMR分类法评价结果的影响有待进一步研究。
| [1] | 宋克志, 李福献, 朱雷敏, 等. 隧道二衬结构受力影响因素的敏感性分析[J]. 公路交通科技, 2014, 31(2):86-91. SONG Ke-zhi, LI Fu-xian, ZHU Lei-min, et al. Analysis on Sensitivity of Influencing Factors of Tunnel Secondary Lining Structure Stress[J]. Journal of Highway and Transportation Research and Development, 2014, 31(2): 86-91. |
| [2] | UNAL E. Design Guidelines and Roof Control Standards for Coal Mine Roofs[R]. State College, PA: Pennsylvania State University, 1983. |
| [3] | GOEL R K, JETHWA J L. Prediction of Support Pressure using RMR Classification[C]//Proceedings of Indian Geotechnical Conference. India:[s.n.], 1991: 48-52. |
| [4] | GOEL R K. Correlations for Predicting Support Pressures and Closures in Tunnels [D]. Nagpur, India: Nagpur University, 1994. |
| [5] | GOEL R K, JETHWA J L, PAITHANKAR A G. Indian Experiences with Q and RMR Systems [J]. Tunnelling and Underground Space Technology, 1995, 10(1): 97-109. |
| [6] | MARINOS V, MARINOS P, HOEK E. The Geological Strength Index: Applications and Limitations[J]. |
| [7] | 靳晓光, 李晓红. 高地应力区深埋隧道软弱围岩支护结构力学特性研究[J]. 公路交通科技, 2008, 25(2): 101-105. JIN Xiao-guang, LI Xiao-hong. Study on Mechanical Properties of Support Structure of Deep Buried Tunnel Soft and Weak Surrounding Rock in High Situ Stress Area[J]. Journal of Highway and Transportation Research and Development, 2008, 25(2): 101-105. |
| [8] | 陈亮, 陈寿根, 张恒. 基于应力路径和塑性评估的应力调整分析方法[J]. 公路交通科技, 2013, 30(10): 80-85, 116. CHEN Liang, CHEN Shou-gen, ZHANG Heng. Analysis Methods of Stress Adjustment Based on Stress Path and Plastic Assessment[J]. Journal of Highway and Transportation Research and Development, 2013, 30(10): 80-85, 116. |
| [9] | 陈德基, 刘特洪. 岩体质量评价的新指标——块度模数[C]//全国首届工程地质学术会议论文选集.北京:科学出版社, 1983:138-145. CHEN De-ji, LIU Te-hong. A New Evaluation Index for Rock Mass Quality: Block Module[C]// Proceedings of the First National Engineering Geological Academic Conference.Beijing:Science Press, 1983:138-145. |
| [10] | 张世殊. 坝基岩体块度特征研究[J]. 工程地质学报, 2001, 9(4): 353-356. ZHANG Shi-shu. The Characteristics of Rockmass Block at Dam Foundation[J]. Journal of Engineering Geology, 2001, 9(4):353–356. |
| [11] | 胡卸文, 钟沛林, 任志刚. 岩体块度指数及其工程意义[J]. 水利学报, 2002, (3): 80-83. HU Xie-wen, ZHONG Pei-lin, REN Zhi-gang.Rock Mass Block Index and Its Engineering Practice Significance [J].Journal of Hydraulic Engineering, 2002, (3): 80-83. |
| [12] | 苏永华, 封立志, 李志勇, 等. Hoek-Brown 准则中确定地质强度指标因素的量化[J]. 岩石力学与工程学报, 2009, 28(4): 679-686. SU Yong-hua, FENG Li-zhi, LI Zhi-yong, et al. Quantification of Elements for Geological Strength Index in Hoek-Brown Criterion [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(4):679-686. |
| [13] | 刘业科, 曹平, 衣永亮, 等. 基于地下深部工程岩体特性的 RMR系统修正[J]. 中南大学学报:自然科学版, 2010, 41(4): 1497-1505. LIU Ye-ke, CAO Ping, YI Yong-liang, et al. Revised RMR System on Underground Deep Engineering Rock Mass Property [J]. Journal of Central South University: Science and Technology, 2010, 41(4): 1497-1505. |
| [14] | 刘焕新, 郭奇峰, 郭乔盛. 考虑地应力损伤的岩体质量分级和岩体力学参数的确定[J]. 中国矿业, 2013, 22(6): 114-117. LIU Huan-xin, GUO Qi-feng, GUO Qiao-sheng. Rock Mass Quality Classification Based on In-situ Stress Damage and Determination of Mechanical Parameters [J].China Mining Magazine, 2013, 22(6): 114-117. |
| [15] | ORESTE P P. Analysis of Structural Interaction in Tunnels Using the Covergence-confinement Approach[J]. Tunnelling and Underground Space Technology, 2003, 18(4): 347-363. |
 2015, Vol. 31
2015, Vol. 31
