扩展功能
文章信息
- 赵明华, 彭珩, 张锐
- ZHAO Ming-hua, PENG Heng, ZHANG Rui
- 方形隧道稳定性极限分析有限元数值模拟
- FE Numerical Simulation for Limit Analysis of Stability of Square Tunnel
- 公路交通科技, 2015, Vol. 31 (5): 107-114
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (5): 107-114
- 10.3969/j.issn.1002-0268.2015.05.018
-
文章历史
- 收稿日期:2014-07-11
隧道的稳定性分析一直是工程领域研究的重点。目前,在隧道稳定性分析计算中常用的方法包括解析法和数值分析法。其中,极限分析解析法因其概念明确、计算简便,广泛地用于求解隧道稳定性问题。Davis[1]等采用极限分析方法求得黏土不排水条件下维持隧道地层稳定所需的最小支护反力;杨峰[2]等在Davis研究基础上,对破坏模式加以改进,并导出支护反力的上限解析公式。但上述研究必须人为假定破坏模式,由于计算模型几何参数和边界条件较为复杂,常造成假定的破坏模式不完全符合实际情况,故其计算结果存在一定的误差。为解决上述问题,不少学者采用数值分析方法对隧道稳定性问题进行研究。贾剑青[3]等利用有限元法研究隧道支护结构的稳定性问题,根据支护结构应力与位移的大小判断其稳定性;许建武[4]等采用有限差分法对隧道稳定性问题进行数值仿真研究,得到各个阶段隧道衬砌应力、应变的规律,从而验证支护方案的合理性。尽管采用有限元法与有限差分法可以有效考虑复杂的几何边界条件、荷载条件以及非均质材料等问题,但不能确定隧道发生破坏时的极限荷载,研究者主要依据应力、应变、位移与塑性区等指标评价其稳定性,属于经验性的判断,而无法定量、准确地判断其稳定性。
为弥补上述方法的不足,有学者提出极限分析有限单元法,其实质是采用数值分析方法求解极限问题,可考虑不同的力学参数与复杂工况,并避开了复杂的应力-应变增量迭代过程,直接针对最终的极限状态进行处理,无需假定破坏模式即可进行稳定性计算,利用计算机自动搜索出连续体破坏时的极限荷载及速度场或应力场。目前,已有部分学者将该方法初步应用于隧道稳定性分析中。例如,姜功良[5]应用上限有限元法求解隧道的稳定系数,获得较为严格的上限解,且与Davis的下限解非常接近;Assadi[6]等采用极限分析有限元法求得隧道稳定系数,并对隧道破坏模式的变化规律进行探讨;Sloan[7]等针对不排水且抗剪强度随深度线性变化的情况,采用极限分析有限元法对隧道稳定性问题进行分析;Wilson[8]等用该方法研究双平行方形隧道的稳定性问题;杨峰[9]等利用上限有限元法对浅埋隧道的稳定性进行探讨,并分析各参数对隧道稳定系数的影响。然而,以上学者提出的稳定系数在工程应用中仍显粗糙,主要针对黏土不排水条件(φ=0),适用范围较为有限。在数值计算过程中,未考虑内摩擦角的影响,土体强度较低,常造成稳定系数计算值较实际值偏大,难以为实际工程提供合理的参考依据。因此,进一步研究考虑内摩擦角影响的隧道稳定性问题是十分必要的。
基于以上原因,本文在前人研究的基础上考虑内摩擦角的影响,采用极限分析有限单元法对方形隧道稳定性问题进行研究。首先,基于合理的计算假定,建立一种可以考虑多种因素影响的简化计算模型;其次,在简化计算模型的基础上,利用极限分析有限单元法计算出不同影响因素下的隧道稳定系数,以此作为评价隧道稳定性的定量判据,根据计算结果拟合出稳定系数的无量纲分析图表和经验计算公式,并基于各参数分析获得隧道破坏模式的变化规律;最后,通过实际算例验证本文方法的可行性。
1 极限分析有限单元法极限分析有限单元法的核心思想是采用有限元将连续体离散化,基于极限分析上、下限定理建立相应的数学规划模型,采用合适的数学规划算法搜索出该模型的最优解。其具体的求解过程可以概括为如下3个主要阶段:(1)单元离散化;(2)数学规划模型的建立;(3)数学规划模型的求解。上述过程通过以数值分析软件Matlab为平台编制相关的计算机程序实现。由于篇幅所限,本文仅对极限分析有限元法的基本求解过程作简要介绍,详细内容可参考文献[10, 11, 12, 13, 14, 15, 16]。
1.1 单元离散化极限分析有限单元法一般采用线性三角形单元对连续体进行离散化。然而,由于线性单元变形自由度很小,难以模拟复杂的速度场和应力场。为克服上述问题,可在相邻单元的公共边上设置速度与应力间断线,使速度与应力在间断线上发生较大跳跃。图 1分别给出线性三角形速度单元和应力单元,单元内速度与应力线性分布,每个节点分别有2个速度分量和3个应力分量。需要说明的是,图中为了表示方便将速度间断线及应力间断线拉开一段距离,其实际厚度为0,即节点1,5和2,4分别重合。
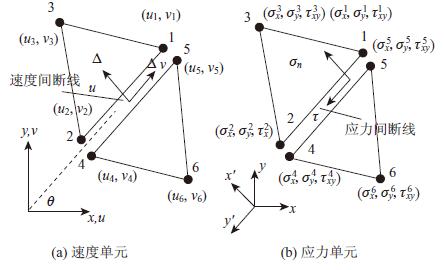
|
| 图1 速度与应力单元示意图 Fig.1 Velocity element and stress element |
在单元离散化的基础上,为寻找一个机动相容的速度场或静力相容的应力场,使得其所对应的极限荷载上限解最小或下限解最大,需要根据上、下限定理的相关要求建立约束方程,并以计算区域总内能耗散或总外力荷载为目标函数,即可得到相应的数学规划模型。因此,完整的极限分析数学规划模型的建立过程如图 2所示。
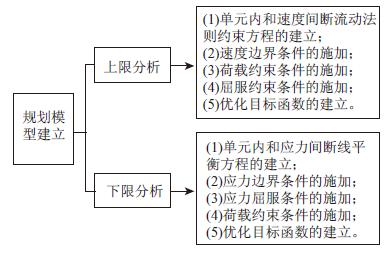
|
| 图2 数学规划模型的建立 Fig.2 Establishment of mathematical programming model |
通过上述步骤,即可得到一个上、下限数学规划模型。为模拟更为复杂的实际工程,提升求解效率,引入非线性数学规划模型,详细内容可参考文献[11, 12]。因篇幅所限,仅给出其具体形式如下:
上限数学规划模型:
目标函数最小值:
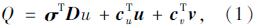
优化条件:
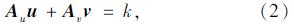
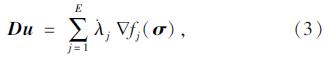

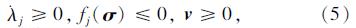
下限数学规划模型:
目标函数最大值:

优化条件:

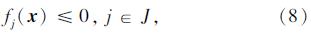
在数学规划模型建立之后,需要采用合适的数学规划手段搜索出其最优解。由1.2节关于数学规划模型的介绍可知,其求解过程极其复杂,涉及众多的变量和约束条件。为了提升求解效率,采用一种高效的非线性规划算法——可行弧内点算法[13,14],对其进行求解,该方法具有快速、易收敛、计算稳定等优点。其求解思路可以概括为:(1)将约束优化问题(1)~(5)或(6)~(8)转化为一组Kuhn-Tucker优化条件[10,11];(2)寻找一个初始可行点,将可行点处约束问题的Kuhn-Tucker优化条件转化为一个线性方程组;(3)对该线性方程组的右端项进行扰动,构造一条可行弧,并沿可行弧进行搜索且使目标函数逐渐减小;(4)重复以上过程,直至得到一个满足Kuhn-Tucker优化条件的最优点。
2 计算假定与有限元模型 2.1 计算假定如图 3所示,假定隧道高度为B,顶板至地表的垂直距离为H,均布支护反力为σt,土体的黏聚力、内摩擦角和重度分别为c,φ,γ。由以上计算参数可知,隧道稳定性问题所涉及的影响因素众多。为了简化计算过程,同时突出主要影响因素的作用,本文作如下假定:
(1)竖向与水平均布支护反力大小相等;
(2)土体为均质各向同性理想弹塑性材料,服从Mohr-Coulomb屈服准则;
(3)地表水平,不考虑偏压荷载的影响,并将隧道洞室的稳定性问题近似简化为二维平面应变问题。
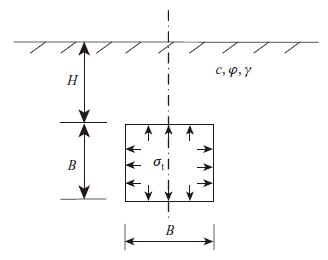
|
| 图3 方形隧道简化计算模型示意图 Fig.3 Simplified calculation model of square tunnel |
根据对称性只需取上述模型的右半侧进行分析,并按照文献[15]介绍的方法构建有限元模型,其中计算网格及边界条件如图 4所示,u与v分别代表水平和竖直方向,σn与τ分别代表法向和切向。为了减少单元数量,加快程序收敛,同时保证计算精度,将计算模型划分为5个区域,按照法向与切向等比插值划分,使得隧道周边范围网格较密,而较远范围网格相对稀疏,并对能量耗散较为集中的1~3区域采用高密度网格划分,4~5区域则采用较稀疏网格划分。
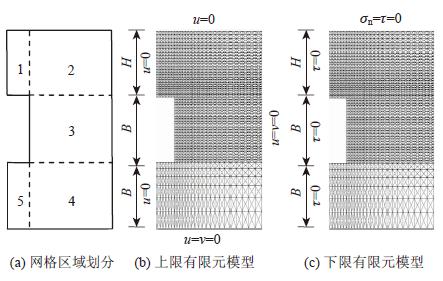
|
| 图4 方形隧道有限元模型示意图 Fig.4 Finite element model of square tunnel |
由2.1节对简化计算模型的描述可知,即使将隧道问题简化为平面问题,涉及的参数仍然很多。为了使计算结果便于工程应用,按照文献[6, 7, 8]中介绍的方法引入一个稳定系数,通常是土体强度参数、结构尺寸和荷载的函数,可以采用极限分析有限单元法求得其临界值,确定极限状态条件下各参数之间的关系。因此,隧道稳定性计算可转化为对体力进行优化,即求解隧道失稳时土体的极限重度,定义如下稳定系数:
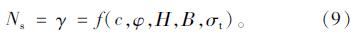
由式(9)可以看出,稳定系数需由5个计算参数确定。若按该式进行分析计算,因各参数之间相互交叉影响,所需计算的数据量非常大,无法突出最重要影响因素的作用。为此,将上述参数无量纲化,可得到如下的稳定系数简化计算公式:
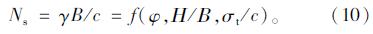
由式(10)可知,稳定系数Ns为土体内摩擦角φ、隧道埋深与其高度之比H/B、支护反力与黏聚力之比σt/c的函数。若φ,H/B,σt/c三者给定,无论c,φ,H,B和σt如何变化,Ns均保持不变。
下文将以图 4中给出的有限元模型为基础,采用极限分析有限单元法对隧道稳定系数Ns进行计算,并给出其无量纲分析图表,如表 1所示。其中计算参数的取值如下:土体强度参数取c=1,φ=0°,5°,…,35°,隧道高度B取单位长度,而埋深H取边长尺寸的倍数,考虑5种不同埋深(H/B=1,2,3,4,5)和6种支护反力(σt/c=0,1,2,3,4,5)。
3.2 稳定系数影响因素分析由表 1可知,隧道稳定系数变化存在以下规律:(1)当埋深一定时,稳定系数随土体内摩擦角和支护反力增大而增大;(2)当其他参数一定时,稳定系数随埋深的增大而减小。
| φ/(°) | H/B | 稳定系数上限值 | 稳定系数下限值 | ||||||||||
| σt/c=0 | σt/c=1 | σt/c=2 | σt/c=3 | σt/c=4 | σt/c=5 | σt/c=0 | σt/c=1 | σt/c=2 | σt/c=3 | σt/c=4 | σt/c=5 | ||
| 0 | 1 | 1.77 | 2.51 | 3.24 | 3.95 | 4.65 | 5.31 | 1.72 | 2.50 | 3.23 | 3.89 | 4.49 | 5.08 |
| 2 | 1.32 | 1.75 | 2.16 | 2.59 | 3.04 | 3.41 | 1.24 | 1.63 | 2.02 | 2.42 | 2.79 | 3.21 | |
| 3 | 1.11 | 1.41 | 1.71 | 2.00 | 2.29 | 2.59 | 1.05 | 1.27 | 1.55 | 1.83 | 2.15 | 2.42 | |
| 4 | 0.96 | 1.19 | 1.42 | 1.65 | 1.87 | 2.10 | 0.91 | 1.13 | 1.35 | 1.56 | 1.78 | 2.02 | |
| 5 | 0.86 | 1.05 | 1.23 | 1.42 | 1.60 | 1.79 | 0.84 | 1.03 | 1.22 | 1.41 | 1.59 | 1.79 | |
| 5 | 1 | 1.93 | 2.85 | 3.75 | 4.62 | 5.49 | 6.36 | 1.97 | 2.85 | 3.73 | 4.59 | 5.45 | 6.31 |
| 2 | 1.56 | 2.06 | 2.59 | 3.11 | 3.65 | 4.16 | 1.52 | 2.10 | 2.56 | 3.09 | 3.61 | 4.10 | |
| 3 | 1.31 | 1.69 | 2.08 | 2.47 | 2.85 | 3.24 | 1.28 | 1.66 | 2.04 | 2.42 | 2.81 | 3.19 | |
| 4 | 1.15 | 1.46 | 1.77 | 2.08 | 2.39 | 2.69 | 1.13 | 1.44 | 1.74 | 2.05 | 2.35 | 2.63 | |
| 5 | 1.05 | 1.31 | 1.57 | 1.83 | 2.08 | 2.34 | 1.01 | 1.28 | 1.52 | 1.79 | 2.03 | 2.28 | |
| 10 | 1 | 2.17 | 3.27 | 4.35 | 5.43 | 6.49 | 7.55 | 2.21 | 3.27 | 4.32 | 5.37 | 6.42 | 7.47 |
| 2 | 1.76 | 2.44 | 3.12 | 3.78 | 4.45 | 5.12 | 1.74 | 2.42 | 3.07 | 3.70 | 4.38 | 5.11 | |
| 3 | 1.55 | 2.07 | 2.58 | 3.09 | 3.60 | 4.11 | 1.50 | 2.01 | 2.51 | 3.01 | 3.51 | 4.00 | |
| 4 | 1.41 | 1.83 | 2.26 | 2.67 | 3.09 | 3.52 | 1.36 | 1.76 | 2.19 | 2.60 | 3.01 | 3.43 | |
| 5 | 1.30 | 1.67 | 2.04 | 2.41 | 2.78 | 3.15 | 1.24 | 1.59 | 1.95 | 2.31 | 2.66 | 3.02 | |
| 15 | 1 | 2.46 | 3.78 | 5.09 | 6.40 | 7.70 | 9.00 | 2.49 | 3.78 | 5.06 | 6.34 | 7.62 | 8.90 |
| 2 | 2.05 | 2.93 | 3.79 | 4.65 | 5.51 | 6.37 | 2.02 | 2.76 | 3.71 | 4.55 | 5.39 | 6.24 | |
| 3 | 1.88 | 2.57 | 3.27 | 3.96 | 4.65 | 5.25 | 1.79 | 2.36 | 3.13 | 3.80 | 4.47 | 5.04 | |
| 4 | 1.79 | 2.34 | 2.95 | 3.55 | 4.16 | 4.75 | 1.66 | 2.14 | 2.82 | 3.41 | 3.98 | 4.53 | |
| 5 | 1.73 | 2.20 | 2.77 | 3.30 | 3.84 | 4.39 | 1.54 | 2.06 | 2.57 | 3.11 | 3.60 | 4.11 | |
| 20 | 1 | 2.80 | 4.40 | 5.98 | 7.56 | 9.14 | 10.71 | 2.81 | 4.37 | 5.94 | 7.50 | 9.05 | 10.60 |
| 2 | 2.49 | 3.57 | 4.70 | 5.84 | 7.03 | 8.10 | 2.35 | 3.45 | 4.55 | 5.67 | 6.73 | 7.86 | |
| 3 | 2.30 | 3.28 | 4.25 | 5.22 | 6.19 | 7.16 | 2.16 | 3.08 | 4.00 | 4.91 | 5.83 | 6.75 | |
| 4 | 2.19 | 3.07 | 3.93 | 4.84 | 5.72 | 6.61 | 2.05 | 2.88 | 3.72 | 4.56 | 5.39 | 6.22 | |
| 5 | 2.13 | 2.97 | 3.80 | 4.65 | 5.53 | 6.33 | 1.94 | 2.71 | 3.47 | 4.24 | 5.01 | 5.76 | |
| 25 | 1 | 3.18 | 5.25 | 7.03 | 8.94 | 10.85 | 12.76 | 3.13 | 5.00 | 6.84 | 8.67 | 10.50 | 12.33 |
| 2 | 2.91 | 4.52 | 6.04 | 7.46 | 9.08 | 10.50 | 2.74 | 4.21 | 5.63 | 7.08 | 8.52 | 9.96 | |
| 3 | 2.81 | 4.22 | 5.62 | 7.02 | 8.42 | 9.72 | 2.59 | 3.87 | 5.15 | 6.43 | 7.72 | 9.00 | |
| 4 | 2.74 | 4.05 | 5.38 | 6.80 | 8.13 | 9.35 | 2.52 | 3.68 | 4.86 | 6.10 | 7.29 | 8.56 | |
| 5 | 2.68 | 3.99 | 5.33 | 6.66 | 7.95 | 9.17 | 2.41 | 3.56 | 4.71 | 5.96 | 7.11 | 8.28 | |
| 30 | 1 | 3.56 | 5.89 | 8.19 | 10.51 | 12.83 | 15.14 | 3.49 | 5.53 | 7.69 | 9.85 | 12.01 | 14.17 |
| 2 | 3.40 | 5.46 | 7.53 | 9.59 | 11.64 | 13.72 | 3.15 | 5.06 | 6.97 | 8.87 | 10.78 | 12.68 | |
| 3 | 3.36 | 5.36 | 7.37 | 9.36 | 11.36 | 13.36 | 3.02 | 4.79 | 6.57 | 8.39 | 10.11 | 11.86 | |
| 4 | 3.22 | 5.24 | 7.23 | 9.25 | 11.21 | 13.22 | 2.89 | 4.62 | 6.36 | 8.02 | 9.75 | 11.43 | |
| 5 | 3.22 | 5.24 | 7.21 | 9.16 | 11.13 | 13.12 | 2.83 | 4.51 | 6.18 | 7.83 | 9.48 | 11.11 | |
| 35 | 1 | 4.15 | 6.98 | 9.71 | 12.56 | 15.35 | 18.16 | 3.70 | 6.29 | 8.86 | 11.42 | 13.99 | 16.55 |
| 2 | 3.99 | 6.65 | 9.26 | 11.90 | 14.55 | 17.27 | 3.57 | 5.95 | 8.34 | 10.75 | 13.18 | 15.52 | |
| 3 | 3.91 | 6.41 | 8.93 | 11.51 | 13.96 | 16.57 | 3.45 | 5.75 | 8.09 | 10.27 | 12.56 | 14.86 | |
| 4 | 3.76 | 6.25 | 8.70 | 11.19 | 13.61 | 16.08 | 3.37 | 5.61 | 7.81 | 10.03 | 12.22 | 14.45 | |
| 5 | 3.71 | 6.13 | 8.50 | 10.93 | 13.32 | 15.77 | 3.31 | 5.58 | 7.76 | 9.86 | 12.10 | 14.27 | |
为了更清楚说明各参数之间的相互关系,根据计算结果绘制相应的关系曲线。图 5分别给出φ=5°,15°,25°,35°时Ns与H/B的关系曲线,其中实线和虚线分别代表隧道稳定系数的上、下限值。从图中可看出,在同一土体内摩擦角条件下,稳定系数随支护反力增大而增大,随H/B增大而逐渐减小,并且当H/B增大到一定值后,稳定系数趋于稳定,表明此时隧道稳定性不再受埋深比的影响,并将该深度视为隧道稳定性不受埋深影响的临界深度。对比图 5可发现,当φ=5°时,稳定系数减小的幅度较大,表明φ较小时,H/B的变化对隧道的稳定性产生显著的影响;而当φ=35°时,稳定系数变化的幅度很小,表明φ较大时,H/B的变化对隧道的稳定性影响甚微。
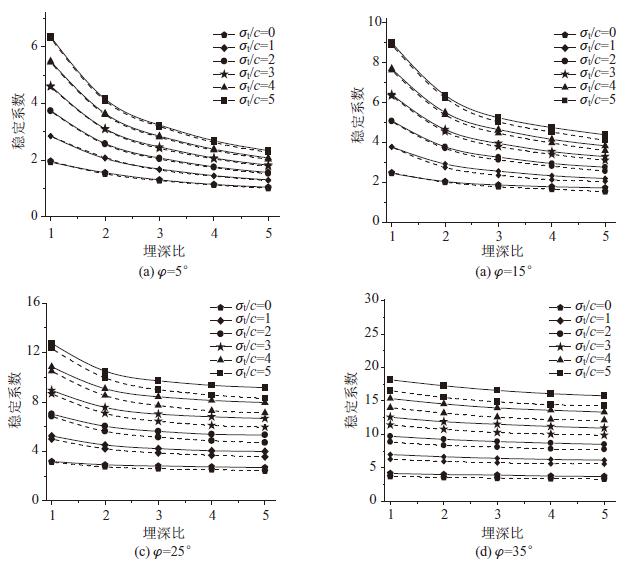
|
| 图 5 稳定系数Ns与H/B的关系曲线 Fig. 5 Relation curves of stability coefficient vs.H/B |
引入稳定系数的概念,不仅能够确定临界稳定条件下各参数之间的关系,而且能够以此作为评价隧道稳定性的定量判据。由式(10)可知,对于特定的φ,H/B,σt/c,利用本文方法可以计算出相应的稳定系数值Ns,然后根据工程实际情况得到Ns′=γB/c。当Ns′≤Ns时,则认为隧道处于稳定状态;反之,则是不稳定的。同时,根据计算结果绘制一系列的稳定系数曲线,依据特定参数从图中查出维持隧道地层稳定所需的最小支护反力σmin。然而,程序的编制和模型的建立较为复杂,在工程应用中存在诸多不便。为此,下文将根据计算结果拟合出稳定系数的经验计算公式,以便工程应用。
根据表 1中数据绘制稳定系数Ns与σt/c,H/B,φ的关系曲线并进行拟合,发现稳定系数与以上参数分别近似呈线性关系、幂关系及指数关系。因此,假设Ns与上述参数的相关经验公式为如下形式:
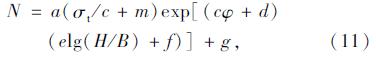
| 拟合系数 | 数值 |
| a | 2.898 75 |
| d | 2.387 58 |
| e | -0.740 50 |
| f | -0.554 59 |
| g | 0.579 39 |
| m | 1.402 12 |
| n | -0.062 51 |
由公式(11)导出维持隧道洞室稳定所需的最小支护反力的经验公式:
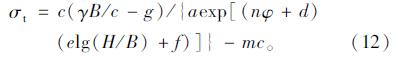
表 3给出H/B=1时数值计算结果平均值与经验公式计算值,两者很接近。由此可见,上述经验公式较为可靠,可满足工程精度要求。
3.4 破坏模式分析由3.2节可知,无量纲参数φ和H/B对隧道稳定性有重要影响。因此,下文将以这两个影响因素为重点,探讨其对隧道破坏模式变化规律的影响。
| φ | 数值计算结果平均值 | 经验公式计算值 | ||||
| σt/c=0 | σt/c=2 | σt/c=4 | σt/c=0 | σt/c=2 | σt/c=4 | |
| 0 | 1.75 | 3.23 | 4.57 | 1.66 | 3.20 | 4.75 |
| 5 | 1.95 | 3.74 | 5.47 | 1.87 | 3.70 | 5.53 |
| 10 | 2.19 | 4.34 | 6.46 | 2.11 | 4.29 | 6.47 |
| 15 | 2.48 | 5.08 | 7.66 | 2.40 | 4.99 | 7.59 |
| 20 | 2.80 | 5.96 | 9.09 | 2.74 | 5.83 | 8.91 |
| 25 | 3.16 | 6.93 | 10.67 | 3.15 | 6.82 | 10.49 |
| 30 | 3.52 | 7.94 | 12.42 | 3.64 | 8.00 | 12.37 |
| 35 | 3.93 | 9.28 | 14.67 | 4.22 | 9.41 | 14.60 |
图 6为H/B=1,5时不同内摩擦角条件下的能量耗散云图。当埋深较小时,随内摩擦角增大,耗散能分布密度较大区域由边墙外侧逐渐变为顶板上部区域,且边墙外侧不再形成明显的剪切带,破裂面由墙顶转角处至地表。然而,当埋深较大时,随内摩擦角增大,边墙外侧剪切带的范围逐渐变小,且耗散能分布区域主要集中于洞周附近,说明该范围发生了较大的塑性变形。这是由于土体拱效应显著发挥,致使破坏区域局限于洞室周边范围。
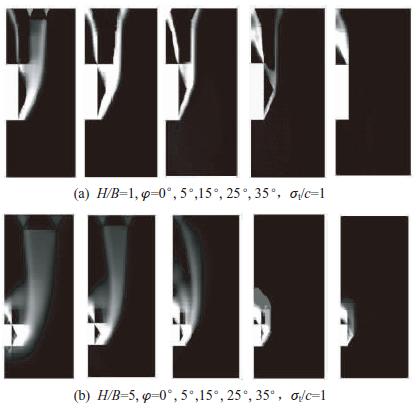
|
| 图6 能量耗散云图 Fig.6 Nephograns of power dissipation |
图 7分别为φ=5°,35°时不同埋深比条件下的能量耗散云图。当内摩擦角较小时,隧道失稳时更容易产生贯通地面的破坏,且随埋深比的增加,耗散能分布较大的区域不再呈明显的线状,而是近似面状。这意味着隧道失稳时产生较大范围的塑性区,外侧剪切带变宽,失稳区域变大。然而,当内摩擦角较大时,破坏模式发生较大变化,耗散能分布区域未向较远处延伸,难以形成贯通至地面的破坏,且随埋深比的增加,破坏区域局限于洞室周边范围,产生明显的拱效应。
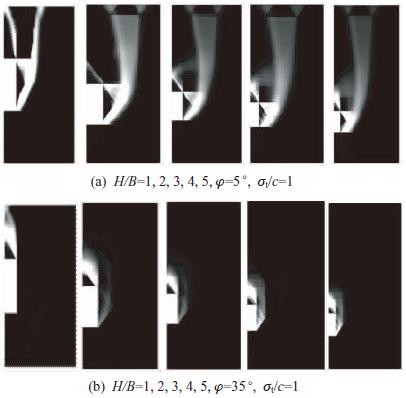
|
| 图7 能量耗散云图 Fig.7 Nephograms of power dissipation |
在实际工程中,隧道失稳往往有其特定的规律,故本文通过对大量的能量耗散云图和速度场图进行分析,总结出其破坏模式存在的相关特征,并以图 8所示工况(H/B=1,σt/c=1,φ=15°)为例作简要介绍:
(1)存在3条明显的剪切带,分别位于顶板上方、边墙外侧和边墙顶部偏下位置。当隧道发生破坏时,被以上剪切带隔开的区域能量耗散较小,可认为这些区域类似于刚体形式运动。
(2)在隧道顶板上方至地表范围内速度方向大致竖直向下,在距离隧道轴线较远的地表附近速度矢量存在水平分量,而地表至边墙外侧区域速度矢量由竖直逐渐向边墙内侧偏转,且洞室周边范围速度矢量值相对较大。
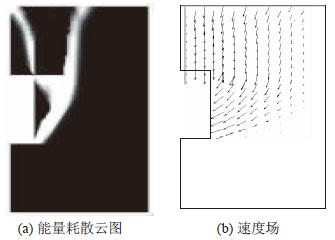
|
| 图8 能量耗散图与速度场(H/B=1,σt/c=1,φ=15°) Fig.8 Power dissipation and velocity field(H/B=1,σt/c=1,φ=15°) |
本文采用文献[3]的算例,选取隧道边长B=10 m,半跨度b=5 m,埋深H=20 m,土体重度γ=20 kN/m3,内摩擦角φ=18°,黏聚力c=10 kPa。按照本文数值方法求解隧道支护反力的上、下限解,将其平均值与文献[3]的上限解作对比,如表 4所示。其中,q,e分别为竖向和水平支护反力,且K=e/q。需要说明的是,本文中的经验计算公式仅适用于q=e(K=1)的情况。
由表 4可知,采用本文数值方法所得结果与已有计算结果很接近,说明本文方法是可行的。
5 结论(1)考虑内摩擦角的影响,使计算模型更符合实际情况。同时引入稳定系数的概念,采用极限分析有限单元法求得稳定系数,以此作为评价隧道稳定性的定量判据,并且所获得的破坏模式能直观地反映实际工程的破坏形态,可为隧道设计提供参考。
(2)隧道稳定系数随H/B增大而减小,随φ和σt增大而增大;当φ较小时H/B的变化对隧道的稳定性产生显著的影响,而当φ较大时H/B的变化对隧道稳定性影响甚微。
(3)当H/B较小时,随φ的增大,边墙外侧不再形成明显的剪切带,破裂面由墙顶转角处至地面;当H/B较大时,随φ的增大,边墙外侧剪切带的范围逐渐变小,耗散能分布区域局限于洞室周边范围。
诚然,因计算中尚未考虑较为复杂的问题,如偏压荷载、非均质材料、三维问题等,故所编制的数值计算程序有待改进,且需更多的工程实践予以验证。
| [1] | DAVIS E H, GUNN M J, MAIR R J, et al. The Stability of Shallow Tunnels and Underground Openings in Cohesive Material[J]. |
| [2] | 杨峰, 阳军生. 浅埋隧道围岩压力确定的极限分析方法[J]. 工程力学, 2008, 25(7):179-184. YANG Feng, YANG Jun-sheng. Limit Analysis Method for Determination of Earth Pressure on Shallow Buried Tunnel[J]. Engineering Mechanics, 2008, 25(7):179-184. |
| [3] | 贾剑青, 王宏图, 李晶, 等. 复杂条件下隧道支护结构稳定性分析[J]. 岩土力学, 2010, 31(11):3599-3603, 3618. JIA Jian-qing, WANG Hong-tu, LI Jing, et al. Stability Analysis of Tunnel Supporting Structure under Complex Condition[J].Rock and Soil Mechanics, 2010, 31(11):3599-3603, 3618. |
| [4] | 杨小礼, 眭志荣. 应力剪胀对浅埋隧道稳定行系数的影响[J]. 中南大学学报, 2008, 39(1):190-195. YANG Xiao-Li, SUI Zhi-Rong. Influences of Stress Dilatancy on Stability Factors of Shallow Tunnels [J]. Journal of Central South University, 2008, 39(1):190-195. |
| [5] | 姜功良. 浅埋软土隧道稳定性极限分析[J]. 土木工程学报, 1998, 31(5):65-72. JIANG Gong-liang. Limit Analysis of the Stability of Shallow Tunnels in Soft Ground [J]. China Civil Engineering Journal, 1998, 31(5):65-72. |
| [6] | ASSADI A, SLOAN S W. Undrained Stability of a Shallow Square Tunnel[J]. |
| [7] | WILSON D W, ABBO A J, SLOAN S W, et al. Undrained Stability of a Square Tunnel where the Shear Strength Increases Linearly with Depth[J]. Computers and Geotechnics, 2013, 49(9):314-325. |
| [8] | WILSON D W, ABBO A J, SLOAN S W, et al. Undrained Stability of Dual Square Tunnels[C]// Proceedings of the 12th International Conference of International Association for Computer Methods and Advances in Geomechanics. Goa: University of Newcastle Press, 2008:4284-4291. |
| [9] | 杨峰, 阳军生, 张学民, 等. 黏土不排水条件下浅埋隧道稳定性上限有限元分析[J]. 岩石力学与工程学报, 2010, 29(增2):3952-3959. YANG Feng, YANG Jun-sheng, ZHANG Xue-min, et al. Finite Element Analysis of Upper Bound Solution of Shallow-buried Tunnel Stability in Undrained Clay[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S2):3952-3959. |
| [10] | 陈惠发. 极限分析与土体塑性[M]. 北京:人民交通出版社, 1975. CHEN Hui-fa. Limit Analysis and Soil Plasticity [M]. Beijing: China Communications Press, 1975. |
| [11] | LYAMIN A V, SLOAN S W. Upper Bound Limit Analysis Using Linear Finite Elements and Non-linear Programming [J]. |
| [12] | LYAMIN A V, SLOAN S W. Lower Bound Limit Analysis Using Non-linear Programming [J]. |
| [13] | HERSKOVITS J, SANTOS G. Feasible Arc Interior Point Algorithms for Nonlinear Optimization[C]// Fourth World Congress on Computational Mechanics. Barcelona:University of Barcelona Press, 1998:356-378. |
| [14] | HERSKOVITS J, MAPPA P, GOULART E, et al. Mathematical Programming Models and Algorithms for Engineering Design Optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(33): 3244-3268. |
| [15] | LYAMIN A V, SLOAN S W. Mesh Generation for Lower Bound Limit Analysis[J]. |
 2015, Vol. 31
2015, Vol. 31
