扩展功能
文章信息
- 潘权, 颜东煌, 许红胜, 王晟
- PAN Quan, YAN Dong-huang, XU Hong-sheng, WANG Sheng
- 轨索移梁新工艺找形分析与试验研究
- Form-finding Analysis and Experimental Research for a New Rail Cable Launching Technics
- 公路交通科技, 2015, Vol. 31 (5): 102-106
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (5): 102-106
- 10.3969/j.issn.1002-0268.2015.05.017
-
文章历史
- 收稿日期:2014-11-13
轨索移梁工艺是地锚式悬索桥主梁架设施工的一种新方法,该工艺依托矮寨悬索桥主梁架设工程,通过整体模型试验[1]、足尺模型试验[2, 3]、实桥验证[4]等,逐步形成了一套新的工艺体系,该工艺流程是:主缆架设完成后,安装永久吊索,以主缆及永久吊索作为支撑,在吊索下方设置吊鞍和水平移梁索道,索道锚固于两岸岩体,分别在两岸组拼钢桁梁标准节段,通过移梁小车将单个节段在移梁索道上纵向运输至永久吊索下方,用跨缆吊机提升钢桁梁节段,节段对接并销接永久吊索,逐节段由跨中向两岸对称施工,直至全桥贯通。矮寨悬索桥1 000.5 m 长的钢桁梁仅用了2.5个月就架设完成[4],大大节省了施工工期和建设成本,体现了新工艺旺盛的生命力。
整个移梁系统由主缆,吊索和移梁索道构成稳定的双层索系,移梁索道既作为稳定索又作为工作索承受移梁小车及钢桁梁节段荷载,且移梁索道与主缆、吊索受力和变形相互耦合。这种双层索系结构分析方法与传统的悬索桥单层索结构的受力分析不同,同时轨索是有预张拉力的柔索结构,索系一旦受力,体系将发生比较明显的变形,通过这种变形将使荷载在索结构系统中按刚度分配,并呈现较强的非线性[2]。已架设的悬索桥主缆截面大,重力刚度大,张紧的轨索截面小,在由轨索和主缆、吊索组成受拉力双层索网中,主缆几乎承担全部重力[2, 3, 5],且由于吊索是柔性索,在轨索张拉荷载作用下会伸长,其变形协调关系中须考虑这个作用,但施工过程中吊索力未知,需要从体系变形协调关系中隐性求解,这就给静力分析和求解带来了难度和复杂性[6, 7]。在该工艺研发过程中,将主缆和轨索均当成分段悬链线用有限元方法求解[8],计算过程较繁杂,且轨索有较大的预张拉力,与只考虑自重作用下的悬索节段受力有一定的差异。为了简化轨索移梁工艺计算分析过程,根据柔索力学分析的基本假定,在吊索力未知的情况下,考虑吊索的弹性伸长,建立主缆、吊索、轨索的整体力学模型并求解,其中主缆节段采用分段悬链线模拟,轨索采用分段抛物线索单元来模拟,吊索用直线索单元模拟,计算结果与有限元计算结果、模型试验结果进行对比分析,结果表明本文分析方法是正确的,可以用到类似结构的工程分析中。
1 轨索移梁工艺空载状态下的力学分析模型定义空载状态为主缆、吊索架设完成,轨索安装就位并张拉完成的状态。为了简化空载状态下体系的计算方法,特做如下假定[9, 10, 11, 12]:
(1)柔索只能受拉,不能受压和受弯。
(2)柔索的应力-应变符合胡克定理。
(3)受力前后主缆、轨索、吊索的抗拉刚度计算时均使用变形前的截面面积。
(4) 忽略轨索与吊鞍座间的摩擦,吊索在轨索张拉完成后不发生倾斜。
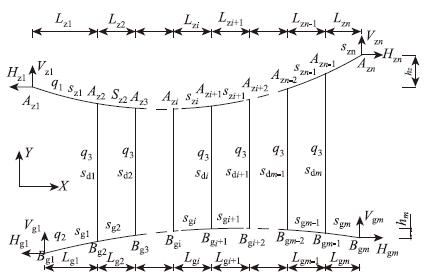
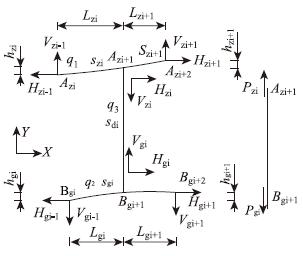
建立如图 1所示的运梁体系空载状态下的力学分析模型,模型中字母z代表主缆、字母g代表轨索、字母d代表吊索,为了描述分析过程,抽取如图 2所示的一个节间模型进行分析。
|
| 图1 轨索移梁空载状态力学分析模型 Fig.1 Mechanical analysis model of rail cable launching undernon-loading condition |
|
| 图2 轨索移梁空载状态力学离散模型 Fig.2 Mechanical dscrete model of rail cable launching under non-loading condition |
如图 2所示,将主缆节段离散为2个节段Azi-Azi+1,Azi+1-Azi+2,分别建立分段悬链线单元方程[9, 10, 11],并求解得lzi,hzi,lzi+1,hzi+1,Szi:
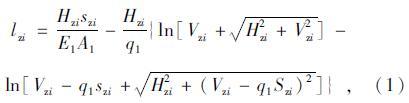
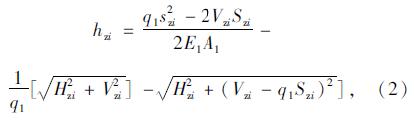
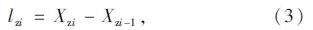
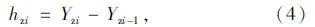
根据Azi节点及吊索受力平衡状态,可以建立另外2个方程(5)、(6)。

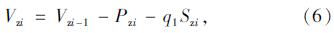
根据轨索支撑条件、应力水平、安全系数、主梁架设过程中体系的平顺性和牵引力等确定轨索直径、强度等级、类型和预张力[5, 8, 13]。由于轨索支撑在与吊索下锚点相连的吊鞍上,轨索节段在自重作用下会产生一定的垂度,在近似计算中,为简化计算分析过程,假定轨索各节段线形均为二次抛物线[7],即把轨索离散成各分段抛物线的连接,用抛物线索单元来模拟轨索节段空载状态下的受力,得到如图 3所示的分析简图。根据静力平衡方程,可以得出抛物线索段的内力和几何方程如式(7)-(15)所示。
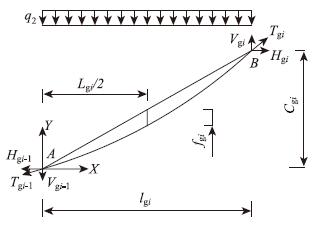
|
| 图3 两节点抛物线索单元离散图 Fig.3 Scattergram of two-node parabolic cable element |
轨索张力的水平分量为

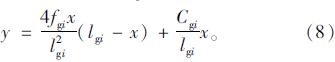
轨索的形状长度为
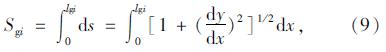
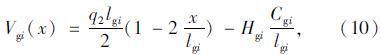
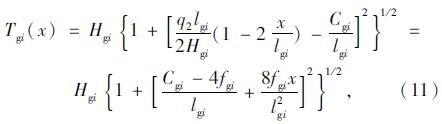

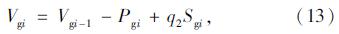
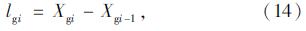
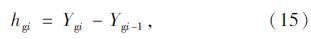
在空载状态下不考虑吊索的倾斜,吊索受力和变形协调关系:
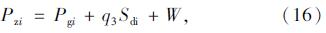
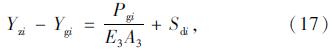
吊索无应力索长Sdi、空缆线形、索力、索塔间距及标高等可以根据成桥状态倒拆确定[9,10]。轨索张拉前锚固点的纵向距离lg可以根据现场施工条件确定,但标高需要从体系迭代中分析求解,轨索预张拉力Tg0在1.2节中分析确定。
1.5 方程求解分析(1)假定轨索左支座处的水平力Hg0和标高hg0,主缆左支座处水平力Hz0,吊索索力增量Pg1;
(2)由式(12),(5)可知Hgi,Hzi;
(3)由式(10),(13),(14),(15),(11)分别得到Vg0、Vg1、lg1、hg1、Tg1;
(4)由式(8),(17),(4)分别得到Yg1、Yz1、hz1;
(5)由式(2),(1)可以求得Vz0、lz1;
(6)由式(16),(6)(13)得到Pz1、Vz1,Vg2;
(7)代入式(2),(1),(11),(14),(15)后求得hz2、lz2、Tg2、lg2、hg2;
(8)由式(4),(16)求得Yz2、Pg2;
(9)按此迭代求得所有的lgi,lzi,hgi,hzi;
(10)检查式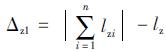 ≤ε(ε为给定的误差限,取1×10-6),
≤ε(ε为给定的误差限,取1×10-6),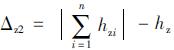 ≤ε,
≤ε,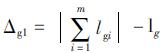 ≤ε,
≤ε,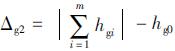 ≤ε、若满足则进行下一步,若不满足,则Hz0=Hz0+
≤ε、若满足则进行下一步,若不满足,则Hz0=Hz0+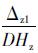 ,Pg1=Pg1+
,Pg1=Pg1+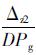 ,Hg0=Hg0+
,Hg0=Hg0+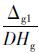 ,hg0=hg0+
,hg0=hg0+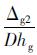 回到(1),重新迭代计算。其中DHz,DPg,DHg,Dhg分别为Δz1,Δz2,Δg1,Δg2对Hz0,Pg1,Hg0,hg0的一阶导数[13]。
回到(1),重新迭代计算。其中DHz,DPg,DHg,Dhg分别为Δz1,Δz2,Δg1,Δg2对Hz0,Pg1,Hg0,hg0的一阶导数[13]。
至此可以求得所有的吊索力和各任意点的坐标,从而求得轨索标高、轨索无应力索长等参数。
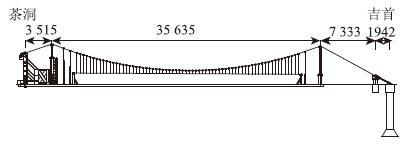
2 轨索移梁空载状态下模型试验为了验证本文分析方法的正确性,在综合考虑试验内容、结构参数、模型材料、制作条件以及试验室的环境条件等因素的基础上,按照1∶33的几何缩尺比设计和制作矮寨悬索桥整体试验模型。缩尺后模型主缆孔跨尺寸为(7.333+35.636+3.515) m,主缆中心间距为818 mm,吊索的纵向间距为439.4 mm,见图 4,试验模型由2个锚碇系统、2根主缆、68对吊索及索夹、3对岩锚索、2个索塔及索塔支墩,轨索及轨索张拉装置、测试系统等组成,具体设计见文献[1]。根据应力一致,轴向刚度相似原则设计轨索各参数,选用4根Φ2.5 mm高强度镀锌钢丝绳等代轨索,设计了轨索张拉和测试装置用以调整和测试轨索力。
|
| 图4 矮寨悬索桥整体模型示意图(单位:mm) Fig.4 Schematic diagram of Aizhai suspension bridge model(unit:mm) |
采用有限元软件MIDAS Civil建模,通过调整试验模型空缆状态,保证空缆状态与有限元分析模型一致。安装完成索夹、吊索、吊鞍,张拉4根轨索,并保证吊索处于垂直工作状态,测试张拉工况下主缆力和线形、岩锚索索力、轨索线形、吊索索力等的变化情况。
3 测试结果分析4根轨索张拉完成后,将整体模型试验测试结果、有限元计算分析结果、本文计算分析结果进行比较,限于篇幅,抽取几个典型位置的响应进行了对比,见表 1。
| 项目 | 中跨跨中主缆变位/mm | 吉首岸侧1/4跨主缆变位/mm | 茶洞岸侧1/4跨主缆变位/mm | 锚固点主缆力/kN | ||||
| X向 | Y向 | X向 | Y向 | X向 | Y向 | 吉首岸侧 | 茶洞岸侧 | |
| 有限元解 | 1.4 | 28.6 | -0.6 | 9.0 | 3.6 | 7.7 | 61.7 | 58.5 |
| 模型试验实测值 | 1.5 | 27.5 | -0.5 | 8.9 | 3.5 | 7.5 | 59.9 | 57.1 |
| 本文计算结果 | 1.6 | 27.3 | -0.6 | 9.0 | 3.5 | 7.6 | 60.1 | 58.0 |
| 有限元解与实测值的偏差/% | -6.67 | 4.00 | 20.00 | 1.12 | 2.86 | 2.67 | 3.01 | 2.45 |
| 本文方法与实测值的偏差/% | 6.67 | -0.73 | 20.00 | 1.12 | 0.00 | 1.33 | 0.33 | 1.58 |
注:实测值为上下游测点的平均值,X向测点向吉首岸侧移动为负,Y向测点向上为负,反之为正。 | ||||||||
从表 1中可以看出,本文分析结果与模型试验实测值、有限元计算值在Y向的偏差较小,最大偏差为1.33%,锚固点主缆力偏差不大,最大为1.58%,中跨跨中、茶洞岸侧1/4跨主缆变位X方向偏差相对较小,吉首岸侧1/4跨主缆变位X向偏差相对较大,主要由于X向总体变形值较小,测试系统的精度等引起了较大的偏差。对比分析结果总体表明本文分析方法能解决轨索移梁体系空载状态下的计算分析和空间找形问题,从而可以简化体系分析过程,计算过程可以直接应用到类似工程结构分析中。
4 结论通过理论推导建立了轨索移梁系统空载状态下的主缆、吊索、轨索的整体力学分析模型,并通过迭代计算求解,编制了对应程序,设计并制作了矮寨悬索桥轨索移梁体系的整体缩尺模型并进行了测试分析,结果表明计算结果与有限元计算结果、模型试验结果吻合良好。本文分析方法是在结构变形后的位置上建立的平衡方程,能进行结构大变形的几何非线性分析,在轨索滑移梁新工艺找形计算分析中,将轨索节段离散成两节点抛物线单元,简化的计算分析过程可以达到足够的精度,能够被工程所应用。
通过假定轨索的初始力或位形进行迭代计算得到轨索的真实内力和几何形状,简化了计算分析过程,是一种新的适合于轨索移梁工艺空载状态下找形分析计算方法。
| [1] | 冯剑.矮寨特大悬索桥缩尺模型设计研究[D].长沙:长沙理工大学, 2010. FENG Jian. Design of Scale Model of Aizhai Suspension Bridge[D].Changsha: Changsha University of Science and Technology, 2010. |
| [2] | 沈锐利, 闫勇, 唐茂林, 等. 轨索滑移法节段足尺模型试验设计与安装[J].桥梁建设, 2013, 43(1):15-22. SHEN Rui-li, YAN Yong, TANG Mao-lin, et al. Design and Installation of Full-Scale Sectional Model for Testing of Rail Cable Launching Method[J].Bridge Construction, 2013, 43(1):15-22. |
| [3] | 闫勇, 沈锐利, 唐茂林, 等. 轨索滑移法节段足尺模型试验研究[J].桥梁建设, 2013, 43(2):46-50. YAN Yong, SHEN Rui-li, TANG Mao-lin, et al. Testing Study of Full-Scale Sectional Model for Rail Cable Launching Method[J].Bridge Construction, 2013, 43(2):46-50. |
| [4] | 易继武, 盛希, 张念来, 等.矮寨特大悬索桥钢桁加劲梁架设方案研究[J].施工技术, 2013, 42(5):9-11. YI Ji-wu, SHENG Xi, ZHANG Nian-lai, et al. Study on the Erection of Steel Stiffening Truss Girder for Aizhai Bridge[J]. Construction Technology, 2013, 42(5):9-11. |
| [5] | 沈锐利, 张丁盛, 沈子钧. 空中客车交通系统悬索结构的力学特性[J].土木工程学报, 2004, 37(4):13-18. SHEN Rui-li, ZHANG Ding-sheng, SHEN Zi-jun.The Mechanical Properties of the Suspension Cable Structure in Aerobus Transit System[J]. China Civil Engineering, Jaurnal 2004, 37(4):13-18. |
| [6] | 张文福, 孙晓刚, 张红星, 等.预应力双层索静力分析的能量变分解[J].空间结构, 2007, 13(1):29-31. ZHANG Wen-fu, SUN Xiao-gang, ZHANG Hong-xing, et al. Energy Variational Solutions for Static Analysis of Pre-stressed Double Layer Suspended Cable Structures[J].Spatial Structures, 2007, 13(1):29-31. |
| [7] | 罗斌, 郭正兴, 王永泉.基于初始平衡态的索段折线模型[J].建筑结构学报, 2010, 31(11):72-77. LUO Bin, GUO Zheng-xing, WANG Yong-quan. Cable Polygon Model based on Initial Equilibrium State[J]. Journal of Building Structures, 2010, 31(11):72-77. |
| [8] | 马碧波.悬索桥轨索运梁系统设计参数与误差影响研究[D].成都:西南交通大学, 2011. MA Bi-bo. Research on Design Parameters and Error Effect of Track-cable Erecting System for Suspension Bridge[D].Chengdu: Southwest Jiaotong University, 2011. |
| [9] | 唐茂林. 大跨度悬索桥空间几何非线性分析与软件开发[D].成都:西南交通大学, 2003. TANG Mao-lin. 3D Geometric Nonlinear Analysis of Long-span Suspension Bridge and Its Software Development[D]. Chengdu: Southwest Jiaotong University, 2003. |
| [10] | 潘永仁, 范立础. 大跨度悬索桥加劲梁架设过程的倒拆分析方法[J].同济大学学报, 2001, 29(5):510-514. PAN Yong-ren, FAN Li-chu. Backward Analysis Method of Long-span Suspension Bridges for Erection of Stiffening Girders[J]. Journal of Tongji University, 2001, 29(5):510-514. |
| [11] | 王雷, 李传习.索单元结构计算的内力全量迭代法[J].公路交通科技, 2011, 28(8):90-94. WANG Lei, LI Chuan-xi. Internal Force Total Iterative Method in Structure Calculation for Cable Element[J]. Highway and Transportation Research and Development, 2011, 28(8):90-94, in Chinese) |
| [12] | 晏致涛, 刘操兰, 李正良.空间悬链线索单元的非线性有限元分析[J]. 重庆大学学报, 2010, 33(10):64-69. YAN Zhi-tao, LIU Cao-lan, LI Zheng-Liang. Non-linear Finite Element Analysis Based on the Spatial Catenary Cables[J]. Journal of Chongqing University, 2010, 33(10):64-69. |
| [13] | 包立新. 高空悬挂运输系统的静-动力研究[D].成都:西南交通大学, 2007. BAO Li-xin. Research of Aerobus Transportation System Static and Dynamic Behavior [D]. Chengdu:Southwest Jiaotong University, 2007. |
 2015, Vol. 31
2015, Vol. 31
