扩展功能
文章信息
- 鲍泽辰, 张克跃, 张继业
- BAO Ze-chen, ZHANG Ke-yue, ZHANG Ji-ye
- 基于大涡模拟的大气边界层全尺寸风场研究
- Research of Full-size Wind Field of Atmospheric Boundary Layer Based on Large Eddy Simulation
- 公路交通科技, 2015, Vol. 31 (5): 95-101
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (5): 95-101
- 10.3969/j.issn.1002-0268.2015.05.016
-
文章历史
- 收稿日期:2014-07-02
2. 西南交通大学 土木工程系, 四川 峨眉 614202;
3. 西南交通大学 牵引动力国家重点实验室, 四川 成都 610031
2. Department of Civil Engineering, Southwest Jiaotong University, Emei Sichuan 614202, China;
3. State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu Sichuan 610031, China
随着现代社会的飞速进步以及工程技术的不断发展,建筑物高度与跨度的记录不断地被刷新。这就要求建筑材料满足轻质高强的要求,但同时带来的弊端就是结构刚度的降低和对风荷载的影响愈发敏感。倘若不能准确地计算出作用在建筑结构上的风荷载,必将给工程结构造成严重的破坏,给人民生命财产带来重大损失,所以确定作用在结构上的风荷载准确数值是结构抗风设计的关键。
建筑工程结构一般处于大气边界层的下垫层,所处的风场是低速、不可压缩黏性流体的湍流运动,结构周围常伴随着分离、再附着、漩涡脱落等复杂流动现象[1]。根据对湍流中各级尺度涡计算精度和控制方程处理方法的不同,CFD技术的模拟方法可分为直接数值模拟法(DNS)、雷诺平均法(RANS)和大涡模拟法(LES)3种。其中,大涡模拟法是结构抗风数值模拟研究中兼顾计算精度和计算效率的主要选择。但其仍有一个关键问题亟待解决,即开发具有近地风特性的入流边界条件[2]。对于开发具有近地风特性入流条件的研究最早多起源于国外学者。Nozawa[3]、Kataoka[4]和Marayama[5]等学者对大气湍流边界层进行数值模拟,将其解作为抗风LES的脉动入口,得到了与试验结果相符的脉动风速时程,并分别对低矮、高层建筑绕流进行了初步的LES研究,预测了平均风压系数、脉动风压系数,评价了结构表面风压的频谱特性,以及来流脉动特性对结构振动特性的影响等。
近些年,随着计算机软硬件性能的不断提高,关于随机脉动风特性入流条件的研究也越来越多。朱伟亮[6]基于大涡模拟对平板湍流边界层进行了模拟,采用拟周期边界条件实现了脉动输入。李启[7]分别采用旋涡法、谱合成法和预前模拟法生成湍流入口风速脉动,得到了预前模拟法所得结果最优且接近真实湍流的结论。王婷婷[8]采用粗糙元配合随机扰动数的数值模拟方法,成功模拟出4类地貌的大气边界层风场。周阳[9]运用前置粗糙元法实现了全尺寸模型的风场模拟,同时分析总结了大涡模拟方法中的关键影响因素。就目前研究来看,前置粗糙元法可以较好地生成满足条件的脉动风场,但受制于有限的计算机计算能力,研究多采用拟周期边界来缩短计算域,无法对湍流场的转捩过程进行观测,且对于增大流场上部的湍流强度要么不予考虑要么采用添加随机扰动数的方法,在数值模拟的真实度上有所欠缺。
本文基于前置粗糙元法,在全尺寸模型中采用粗糙元、扰流杆与格栅3者组合的数值模型,生成随机脉动的大气边界层风场。参考指标为平均风剖面和湍流强度剖面,模拟目标分别为中国规范指数律风剖面和中国规范湍流强度剖面[10]。
1 数值方法 1.1 基本方程本文采用的湍流模型为大涡模拟,其在笛卡尔坐标系下空间网格滤波后的不可压缩流体连续方程及N-S方程为:

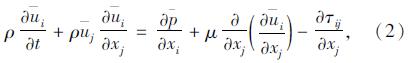
式中,xi和xj为笛卡尔坐标;带上划线的量为滤波后的场变量;i和j为滤波后的速度;为等效压力;ρ和μ分别为流体的密度和动力黏性;τij=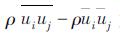 为亚格子尺寸应力,它是可解尺寸与亚格子尺寸能量交换的纽带。
为亚格子尺寸应力,它是可解尺寸与亚格子尺寸能量交换的纽带。
在大涡模拟控制方程求解过程中,对压力项采用standard离散格式,动量采用bound central difference离散格式。数值计算方法采用SIMPLE算法,亚格子应力模型采用Smagorinsky-Lily模型,其中Smagorinsky常数C取为0.1。
1.2 数值模型1969年,Lettau[11]提出了最初的粗糙模拟元模型;Wooding[12]随后又提出了由于粗糙元排列将产生拖曳力的理论;Sigal和Danberg[13]分别提出了对Lettau粗糙元模型的改进模型;Raupach[14]又在拖曳理论上继承和发展了粗糙元模型,并进行了模型参数的讨论。简要地说,最基本的模型方程及相应的输入参数见式(3)[15]:
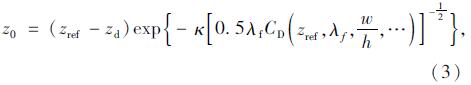
在对于粗糙元法产生一定边界层厚度的研究中,Simiu和Scanlan[16]提出了预估边界层厚度的公式:
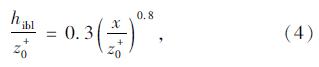
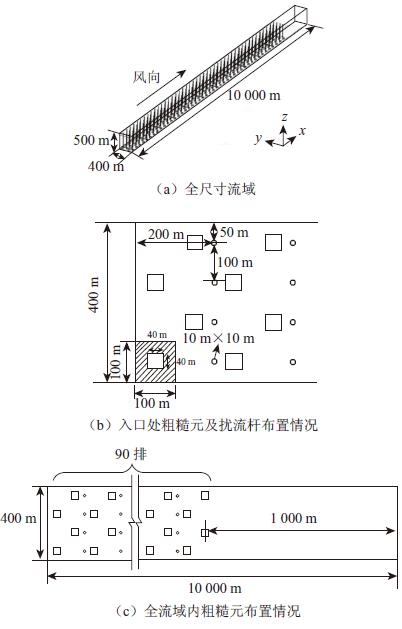
结合先前的研究成果,本文拟采用错列的方法对粗糙元进行布置。选用以底面尺寸为40 m×40 m的长方体为粗糙元,通过变化粗糙元高度以满足不同参数的模拟风场。以高度为40 m的立方体粗糙元为例,λf=wh/dxdy=(40×40)/(200×100)=8%>5%;流域长x应满足x/h>250,即x=250×40 m=10 000 m。同时为增大边界层上部的湍流强度,在粗糙元间隙中布置了数根底面为10 m×10 m的扰流杆,以排为单位规则地布置在流域中,具体的间距将根据不同的风场需要进行设置。
为遵从以上各参数的要求,建立数值模型,如图 1所示。
|
| 图1 数值模型 Fig.1 Numerical model |
为更准确地得到风速的脉动时程,本模型采用结构化网格,在流向与展向采用均匀网格,在竖向对近地面进行加密,网格数约为325万。湍流模型选用大涡模拟,进行非稳态数值计算,时间步长设置为0.01 s。边界条件的选择如表 1所示。
| 模型 | 边界条件 | 模型 | 边界条件 |
| 入口 | 速度入口(指数风) | 展向侧面 | 周期性边界 |
| 出口 | 压力出口 | 粗糙元 | 非滑移壁面 |
| 顶面 | 滑移壁面 | 扰流杆 | 滑移壁面 |
| 底面 | 非滑移壁面 | 展向格栅 | 滑移壁面 |
为在全尺寸模型中采用绕流杆和滑移格栅配合错列粗糙元的数值模型,以便生成随机脉动风场,本节具体针对粗糙元、绕流杆及滑移格栅三者对脉动风场的影响进行数值分析,参考指标为平均风剖面和湍流强度剖面,参考目标分别为中国规范指数律风剖面和中国规范湍流强度剖面,并总结其影响规律。
2.1 粗糙元高度对表 2中列出的粗糙元高度分别为10,20,30,40,50 m共5种工况分别进行LES数值模拟。
| 工况 | 粗糙元高度/m | 绕流杆间距 | 入口风速指数 |
| C10 | 10 | 0(未设置) | α=0.16 |
| C20 | 20 | 0(未设置) | α=0.16 |
| C30 | 30 | 0(未设置) | α=0.16 |
| C40 | 40 | 0(未设置) | α=0.16 |
| C50 | 50 | 0(未设置) | α=0.16 |
在流场出口的中轴线位置上,沿高度方向分别对平均速度与湍流强度剖面进行统计。平均风速剖面的影响如图 2(a)所示,与入口(α=0.16的指数剖面)平均速度相比,粗糙元对边界层下部的流场产生了阻碍作用,且其阻碍作用与影响范围随粗糙元高度的增大而增大,可以观察到下部流场的平均风速剖面形状发生了显著变化。这说明在设定入口平均速度时,一方面应适当增大剖面指数,另一方面在增大边界层下部的湍流强度时,粗糙元高度的设定应以不显著改变剖面形状为前提。湍流强度受到的影响变化如图 2(b)所示,由于布置了粗糙元,相比平板湍流边界层模拟,粗面湍流边界层下部湍流度明显增大,且其增大作用与影响范围同样随着粗糙元高度的增大而增大,可估计其对湍流强度的影响范围大致为粗糙元高度的5~8倍。但粗糙元对上部的湍流强度增大作用极不明显,例如工况C30的下部湍流度剖面与中国规范C类地貌的湍流强度剖面(曲线China_C)基本保持一致,但当高度到达200 m后,湍流强度迅速下降,在350~500 m 高度区间几乎已不存在脉动风现象。

|
| 图2 粗糙元高度变化对湍流场的影响 Fig.2 Influence of roughness elements height on fluctuating wind field |
在前节的数值模型介绍中已谈到扰流杆被布置于底面粗糙元的间隙中,每排4根,展向间距100 m,侧边杆距计算域侧壁50 m,以满足展向周期边界条件,以排为单位沿流向布置在流域当中。第1排扰流杆距入口200 m,此后的扰流杆等间距地布置在流域当中,间距为N×100 m,最后一排以不超过9 000 m为标准,即间距越小扰流杆排数越大。N取1,2,3,4,5共5种工况,如表 3所示。
| 工况 | 粗糙元高度/m | 变量N | 绕流杆流向间距/m | 入口风速指数 |
| R1 | 0 | 1 | 100 | α=0.16 |
| R2 | 0 | 2 | 200 | α=0.16 |
| R3 | 0 | 3 | 300 | α=0.16 |
| R4 | 0 | 4 | 400 | α=0.16 |
| R5 | 0 | 5 | 500 | α=0.16 |
在流场出口的中轴线位置上,沿高度方向分别对平均速度与湍流强度剖面进行统计。平均风速剖面的影响如图 3(a)所示,与入口(α=0.16的指数剖面)平均速度相比,粗糙元对边界层流场产生了阻碍作用,特别是边界层上部的阻碍作用更为明显,当N=5时,平均速度剖面在上部保持较好,而在下部,与入口速度剖面相比已有较为明显的变化。当N的取值继续变小,即继续缩小扰流杆间距时,平均速度出现明显衰减,说明阻力在逐渐增大。当N=1时,上部速度已与α=0.12的剖面基本吻合,这说明在模拟不同剖面速度时,模型入口的剖面指数应适当放大,以弥补扰流杆对风速的阻碍作用。湍流强度受到的影响变化如图 3(b)所示,扰流杆对边界层上部湍流强度的

|
| 图3 扰流杆间距对湍流场的影响 Fig.3 Influence of spoiler lever spacing on fluctuating wind field |
增大作用极为显著,且在150~500 m高度区间湍流强度将基本在一个恒定值附近保持上下浮动,例如工况R3的曲线就与中国规范B类地貌的湍流强度剖面(曲线China_B)在流域上部基本吻合,但其对下部湍流强度有所增大但并不如粗糙元的增大作用那样明显。受模型上部边界条件的影响,湍流强度在接近模型顶面处均有一定增大。
与粗糙元对湍流强度的影响对比可知,粗糙元的影响范围与扰流杆的影响范围具有良好的互补性,可根据不同的地貌湍流强度要求,对二者进行组合配置。
2.3 展向格栅的配置通过观察仅组合了粗糙元与扰流杆的边界层脉动风场发现,粗糙元上部附近的湍流强度有突变的趋势,剖面曲线不够平滑。因此考虑在扰流杆下部添加一道展向滑移格栅,以辅助增大底部的湍流强度。
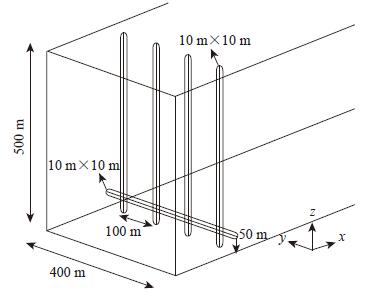
由于目的只考虑增加粗糙元上部附近的湍流强度,计算模型直接选取拟C类地貌流场模型,即高度为30 m的粗糙元与间距为200 m的扰流杆模型配置组合。同时考虑每两道扰流杆布置一道格栅,格栅的展向截面为10 m×10 m,布置于扰流杆下部距地面50 m的位置,格栅模型见图 4,格栅的边界条件选用滑移壁面。
|
| 图4 展向格栅模型 Fig.4 Model of spanwise grille |
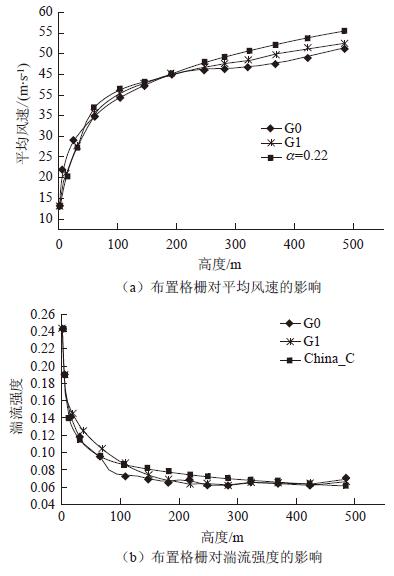
在流场出口的中轴线位置上,沿高度方向分别对平均速度与湍流强度剖面进行统计。平均风速剖面的影响如图 5(a)所示,未布置格栅(G0)与布置格栅(G1)的工况平均风速剖面近似,在50~150 m高度区间内。由于布置的格栅对该区间的风速有一定的阻碍作用,工况G1的平均风速与工况G0相比略有下降。湍流强度受到的影响变化如图 5(b)所示,对比于仅布置了粗糙元和扰流杆的工况G0,布置了展向格栅的工况G1明显增大了粗糙元上部附近的湍流度,并且使得湍流强度剖面的变化更为平滑。
|
| 图5 布置格栅对湍流场的影响 Fig.5 Influence of grille on fluctuating wind field |
本节将以C类地貌为例提出对大气边界层风场的模拟方法。对比各国的建筑规范,本文选定的参考指标为平均风剖面和湍流强度剖面,模拟目标分别为中国规范指数律风剖面和中国规范湍流强度剖面。
模拟的基本思路是:在全尺寸模型中,由于粗糙装置的阻碍作用,在设置入口条件时预先放大相应的中国规范指数律风速剖面,通过调整粗糙元、扰流杆及格栅的配置组合,对湍流度剖面目标曲线进行逼近,最后得到满足规范的大气边界层时程数据。
下面以C类地貌风场为例介绍如下:
(1)适当放大指数风速剖面,我国建筑规范的C类地貌风场的指数α=0.22,在设置时取α=0.24。
(2)选择合适的粗糙元高度,使近地面的湍流度水平与规范近似,这里选取粗糙元高度为30 m。
(3)选择合适的扰流杆间距,使边界层上部的湍流度水平与规范近似,并观察粗糙元上端附近是否出现湍流度变化不平缓的现象,若有则添加展向格栅增大该区间的湍流度,最终得到目标剖面。这里扰流杆间距选取200 m,并设置间距为400 m的展向格栅。
(4)在出口处剖面中心线上选取一系列点作为监测点。根据监测点的速度时程得到最终的平均速度与湍流强度剖面,与我国建筑规范作比较,观察是否完全吻合。
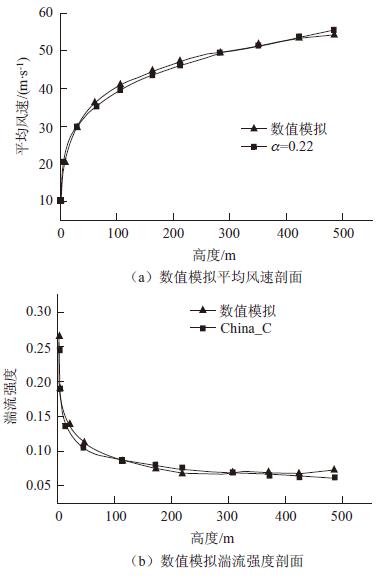
将最终的数值模拟结果与我国建筑规范对比。如图 6所示,在图 6(a)中可见模拟结果的平均速度剖面与α=0.22的指数风速剖面吻合良好,图 6(b)中模拟结果的湍流强度剖面与标注为China_C的我国建筑规范C类地貌湍流强度剖面同样吻合良好。
|
| 图6 C类地貌风场数值模拟与中国建筑规范比较 Fig.6 Comparison of numerical simulation of Class C landscapes wind field with Chinese building code |
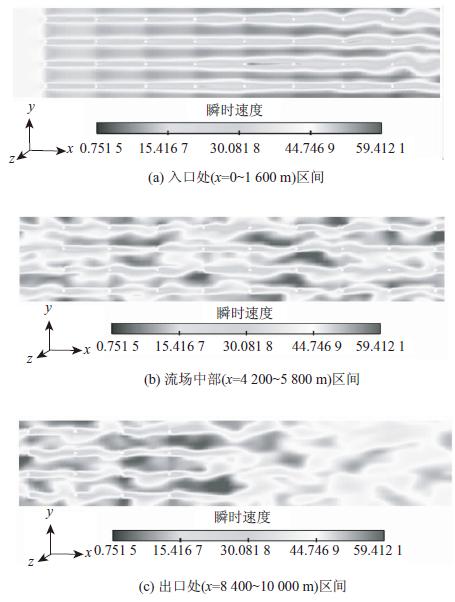
如图 7所示,从t=600 s时高度为z=150 m处截面的流场前、中、后3个部分的瞬时风速云图中可观察到随机脉动风的形成过程。在经过流场中粗糙构件的阻碍后,平均风被动地转捩为脉动风,经过出口前一段距离的自由发展,湍流已发展稳定。
|
| 图7 z=150 m截面瞬时速度云图(t=600 s)(单位:m/s) Fig.7 Instant velocity nephograms of section z=150 m (t=600 s) (unit: m/s) |
本文通过改变粗糙装置的取值使模拟得到的风场特征参数逼近模拟目标,最终生成满足目标要求的大气边界层风场,实现了大气边界层风场的LES模拟。现将所得结论总结如下:
(1)验证了生成大气边界层风场脉动入口数值方法的可行性,即在前置粗糙元法的研究基础上,通过布置粗糙元、扰流杆与展向格栅的方法实现了对边界层风场湍流度的改变,以生成建筑规范中不同地貌类别的大气边界层风场。
(2)通过布置粗糙元可以增加流场底部的湍流度,通过布置扰流杆加大流场上部的湍流度,展向格栅的作用在于增大粗糙元与绕流杆影响范围中间部分的湍流扰动。粗糙元的高度主要影响流场近地面的风场特性。随着粗糙元高度的增加,近地面处的湍流强度随之增大,且其影响范围大致为粗糙元高度的5~8倍。扰流杆对流场上部湍流度增大作用明显,且其效果随着扰流杆的密度增大而增大。
(3)实现了对边界层湍流转捩的全过程模拟,得到的时程数据为后续的结构绕流大涡模拟提供了有价值的来流生成方法。
| [1] | 朱伟亮, 杨庆山.湍流边界层中低矮建筑绕流大涡模拟[J].建筑结构学报, 2010, 31(10):41-47. ZHU Wei-liang, YANG Qing-shan. Large Eddy Simulation of Flow around a Low-rise Building Immeresed in Turbulent Boundary Layer[J]. Journal of Building Structures, 2010, 31(10):41-47. |
| [2] | 朱伟亮, 杨庆山, 曹曙阳.建筑LES模拟脉动入口的适用性研究[J].空气动力学学报, 2011, 29(1):124-128. ZHU Wei-liang, YANG Qing-shan, CAO Shu-yang. Applicability Research on the Turbulent Inflow for Building LES Simulation[J]. Acta Aerodynamica Sinica, 2011, 29(1):124-128. |
| [3] | NOZAWA K, TAMURA T. Large Eddy Simulation of the Flow around a Low-rise Building Immersed in a Rough Wall Turbulent Boundary Layer[J]. |
| [4] | KATAOKA H. Numerical Simulations of a Wind-induced Vibrating Square Cylinder within Turbulent Boundary Layer[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(10/11): 1985-1997. |
| [5] | MARAYAMA Y, RODI W, MARUYAMA Y, et al. Large Eddy Simulation of the Turbulent Boundary Layer behind Roughness Elements Using an Artificially Generated Inflow[J]. |
| [6] | 朱伟亮, 杨庆山.基于LES模型的近地脉动风场数值模拟[J].工程力学, 2010, 27(9):17-21. ZHU Wei-liang, YANG Qing-shan. Large Eddy Simulation of Near Ground Turbulent Wind Field[J]. Engineering Mechanics, 2010, 27(9):17-21. |
| [7] | 李启, 杨庆山, 朱伟亮.湍流入口条件下建筑非定常风场的大涡模拟[J].工程力学, 2012, 29(12): 274-280. LI Qi, YANG Qing-shan, ZHU Wei-liang. Large Eddy Simulation of unsteady Wind Field around Building Using Turbulent Inflow[J]. Engineering Mechanics, 2012, 29(12):274-280. |
| [8] | 王婷婷, 杨庆山.基于FLUENT的大气边界层风场LES模拟[J].计算力学学报, 2012, 29(5): 734-739. WANG Ting-ting, YANG Qing-shan. Large Eddy Simulation of Atmospheric Boundary Layer Flow Based on FLUENT[J]. Chinese Journal of Computational Mechanics, 2012, 29(5):734-739. |
| [9] | 周阳.建筑物脉动风压场大涡模拟入流边界条件的生成研究[D].广州:广东工业大学, 2012. ZHOU Yang. Generation of Large-eddy Simulation Inflow Boundary Conditions on BuildingFluctuating Wind Pressure Field[D]. Guangzhou: Guangdong University of Technology, 2012. |
| [10] | GB50009—2001, 建筑结构荷载规范[S]. GB50009—2001, Load Code for the Design of Building Structures[S]. |
| [11] | LETTAU H. Note on Aerodynamic Roughness-parameter Estimation on the Basis of Roughness-element Description[J]. |
| [12] | WOODING R A, BRADLEY E F, MARSHALL J K. Drag due to Regular Arrays of Roughness Elements of Varying Geometry[J]. |
| [13] | SIGAL A, DANBERG J E. New Correlation of Roughness Density Effect on the Turbulent Boundary Layer[J]. AIAA Journal, 1989, 28(3):554-556. |
| [14] | RAUPACH M R. Drag and Drag Partition on Rough Surfaces[J]. |
| [15] | BOTTEMA M. Urban Roughness Modeling in Relation to Pollutant Dispersion[J]. |
| [16] | SIMIU E, SCANLAN R H.风对结构的作用: 风工程导论[M].刘尚培, 等译.上海:同济大学出版社, 1992. SIMIU E, SCANLAN R H. Wind Effect on Structure: Wind Engineering Introduction [M]. LIU Shang-pei, et al. translated. Shanghai: Tongji University Press, 1992. |
 2015, Vol. 31
2015, Vol. 31
