扩展功能
文章信息
- 杨志刚, 李鹏飞, 李湛
- YANG Zhi-gang, LI Peng-fei, LI Zhan
- 幅值相关阻尼在车桥耦合振动计算中的应用
- Application of Amplitude Related Damping in Calculation of Vehicle-bridge Coupling Vibration
- 公路交通科技, 2015, Vol. 31 (5): 88-94
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (5): 88-94
- 10.3969/j.issn.1002-0268.2015.05.015
-
文章历史
- 收稿日期:2015-03-03
2. 交通运输部公路科学研究院, 北京 100088
2. Research Institute of Highway, Ministry of Transport, Beijing 100088, China
桥梁的车桥耦合振动是桥梁在服役期间最为常见的动力学问题,许多桥梁因为车桥共振的问题产生了众多问题。由于车辆的荷载和行驶振动,对桥梁会产生一定的冲击作用,引起桥梁的振动,并降低桥梁的可靠性,同时对桥梁的疲劳性能也起到恶化的作用。另外桥梁的振动也会对车辆的振动产生反馈作用,使得行车的舒适性变差。对于车桥耦合的计算和控制,早已经引起了学者的重视。
在桥梁的车桥耦合计算中,阻尼一直以来没有明确的界定。这是由于:(1)车桥耦合振动计算没有相关的规范规定,大家的计算都是以理论分析为主,阻尼的取值主要是沿用抗震规范的取值;(2)不同的桥梁阻尼的取值有着较大差距,测试阻尼的离散性,进一步加剧了阻尼取值的不确定性。在桥梁结构车桥耦合振动计算中,阻尼比是动力学方程计算的一个重要的参数。在中国桥梁和建筑结构的设计与分析中,对于阻尼性能的处理还较为粗浅。公路桥梁抗风规范(JTG/T D60—01—2004)中规定[1]:“钢桥阻尼比为0.005,钢混组合梁桥为0.01,混凝土桥为0.02”,公路桥梁抗震设计细则(JTGTB02—01—2008)和建筑抗震设计规范(GB50011—2010)在反应谱分析中均规定[2, 3]:“除有专门的规定以外,结构的阻尼比应取0.05;当按照规定阻尼比不取0.05时,应按照相应的公式调整阻尼修正系数”。欧洲规范(Eurocode 8: Design of structures for earthquake resistance—2001)[4]和美国加州规范(Seismic design criteria—2010)[5]也对阻尼比的取值有类似的规定。综合国内外的相关规范来看,没有针对于阻尼取值的具体条文规定,都是建议取值5%。虽然已经意识到阻尼比的不同对结构响应影响较大[6, 7],并提出了相关的修正系数,但是各种结构的阻尼比的具体取值仍是一个难点。
尽管桥梁的车桥耦合振动和地震动作用下的震动的都属于桥梁的动力学问题,但是二者有着本质的区别。车桥耦合振动主要是小振幅,弹性阶段的高频振动;地震动作用下桥梁的动力响应为大振幅,弹塑性阶段的震动。车振和地震作用使得结构物在振动过程中表现的特征有较大区别。所以在车桥耦合振动计算中,阻尼比采用抗震规范的阻尼比是不合理的。
为了更加精确地计算车桥耦合振动,本文编制了桥梁车桥耦合振动计算的程序,分别利用常阻尼比5%、振动幅值相关阻尼和振动加速度幅值相关阻尼计算了实际桥梁在不同车辆荷载和不同车速作用下的车桥耦合振动响应,并同实际测试的结果进行了比较,验证了不同阻尼模型的优劣性。
1 结构幅值相关阻尼的研究现状针对于建筑结构阻尼比,世界上开展了一系列的测试和分析。Carroll[8]收集了151座建筑物的实测阻尼比数据,经分析得到阻尼比的大小和结构的振动幅度相关;Lagomarsino[9]收集了182座建筑物的实测阻尼比资料,得到阻尼比的大小和结构的自振频率相关;Suda[10]收集了日本123座钢结构建筑和66座钢筋混凝土建筑的阻尼比,通过分析比较发现:阻尼比离散性较大,它与结构的质量、基础类型、使用年限、振动幅度以及阻尼比测试方法相关;Jeary[11]结合建筑的实际测试结果,提出了结构的阻尼比与振动幅度相关,并给出了阻尼比和振动幅度关系的建议表达式:
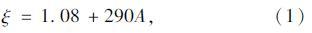
Glanville[12]利用强迫振动激励对3种结构物:钢塔、钢筋混凝土建筑物、人行天桥进行了测试,结果发现结构的阻尼比与风速、结构位移、结构自振频率相关,但未给出相关的关系式;Li[13, 14, 15]测试了金茂大厦等高层建筑在台风作用下的纵横向的阻尼比,其值分别为0.57%和0.55%,远小于实验室模型测试结果,并发现阻尼比随着振幅的增大而增大。Rachel Bashor[16]对三座建筑物在低幅振动下进行多年的持续性动力性能监测,所测阻尼比数据离散性远大于自振频率数据,阻尼比的大小与结构的加速度有着一定的联系。
针对于桥梁结构的阻尼比,国际上也开展了一系列的研究。Eyre[17]和Tilly[18]利用自由衰减法,测试了23座钢桥和组合桥(跨度范围17~213 m),测试结果发现,阻尼比与振幅有着明显的非线性关系,振幅越大,阻尼比数值越大。高振幅测试的阻尼比要比低振幅测试的阻尼比大4倍。这主要是由于低振幅下阻尼的贡献都是材料阻尼,高振幅下阻尼的贡献还包括了节点和基础的作用。同时也发现了桥梁阻尼比与频率的关系,并给出了建议的阻尼比范围。钢桥的建议阻尼比范围为2%~6%,组合桥梁为5%~10%,钢筋混凝土桥为2%~10%。Green和Cebon[19]对两座公路桥进行了冲击荷载下的动力测试,测试得到的阻尼比发散严重,从1.4%~8.8%,作者无法解释这种现象,推测为激励力的大小造成的。Green[20]收集了加拿大安大略省1956—1971年测试的一些桥梁的阻尼比,收集的数据显示桥梁跨度小于75 m的阻尼比的范围在0.15%~0.64%,桥梁跨度大于125 m的阻尼比范围在0.64%~0.95%。Billing[21, 22]对加拿大安大略省的27座钢桥、木桥和混凝土桥进行了测试,激励方式为跑车试验,测试的钢桥阻尼比范围为0.4%~0.7%,混凝土桥的阻尼比范围为0.8%~3.8%。
Casas[23]测试了一座斜拉桥的动力性能,发现阻尼比与桥梁的振动幅度关系较大,但未获得明确的关系;Myrvoll等[24]测试了一座斜拉桥的动力特性,测试结果表明,阻尼比数值小于0.5%,远小于设计的阻尼比,这与测试时振动幅度相关。Filipe等[25]分别利用自由衰减和环境振动激励测试了3座结构(体育场、人行天桥、斜拉桥)的阻尼比,测试结果发现环境激励下测试便捷但结果离散性较大,多次测量取平均值与自由衰减测试的结果差距不大。 Rebelo等[26]利用自由衰减和环境激励下的振动测试了6座位于奥地利的中小跨铁路桥梁的动力特性,结果表明:列车通过后自由衰减测试的阻尼比远大于环境激励下测试的阻尼比,列车激励下自由衰减测试的阻尼比一般大于5%,而环境激励下的阻尼比为2%左右。 Kaustell和Karoumi[27, 28]通过试验研究表明铁路钢混组合桥梁的阻尼比和振幅及加速度有很大的正相关性,并给出了阻尼比和振动加速度的关系式:
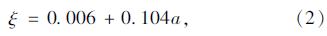
综合上面的介绍,发现针对于建筑结构和桥梁结构,大规模的结构阻尼特性的调查测试分析得到开展。幅值相关的阻尼特性已经引起了众多研究者的重视。本文选取文献[11]和文献[27]的幅值相关模型计算分析桥梁的车桥耦合振动。
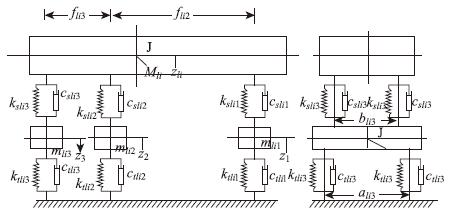
2 车桥耦合振动方程的建立根据文献[29]提出的车辆简化模型,本文将行使在桥上的汽车,简化为车体、支悬装置和车轴及轮胎。车辆自身振动主要概括为:车体的竖向振动、纵向摇摆振动和横向摇摆振动,以及轮对的竖向振动和横向摇摆振动。本文应用的三轴车的示意图如图 1所示。
|
| 图 1 三轴汽车模型 Fig. 1 Tri-axle vehicle model |
车辆采用总重为325 kN的三轴载重车,前轴重65 kN,中轴、后轴重均为130 kN;前、后轴悬挂弹簧刚度分别为500,1200 kN/m;前、后轴悬挂弹簧阻尼分别为10,16(kN·m-1)/s;轮胎刚度取2300 kN/m,轮胎阻尼取16(kN·m-1)/s。
2.1 车辆运动的能量计算(1)车辆动能
车辆的动能包括车体和车轴的竖向振动动能、车体和车轴的横向摇摆动能、车体的纵向振动动能,计算公式如式(3)所示:
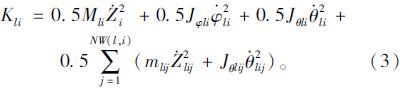
(2)弹簧的弹性势能
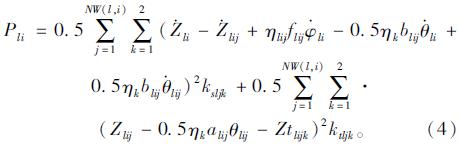
(3)阻尼耗散能量
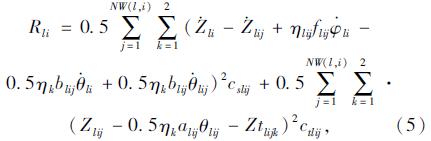
然后将上面的各项能量表达式,代入拉格朗日方程,可以得到车辆的运动方程。
2.2 车辆的运动方程(1)车体运动方程
车体的运动方程有3个,包括车体的竖向振动,点头(车体前后的竖向振动),侧滚(横向振动),分别如式(6)、(7)、(8)所示:
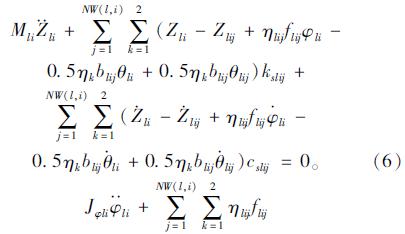
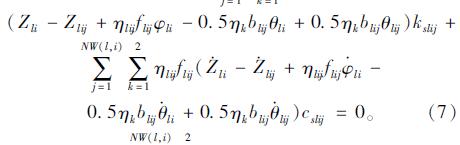
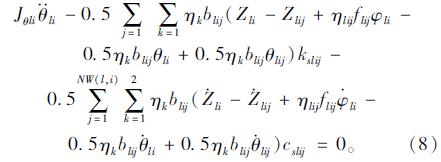
(2)轮对的运动方程
轮对的运动方程包括轮对的竖向振动和横向振动,具体表达式如式(9)、(10)所示。
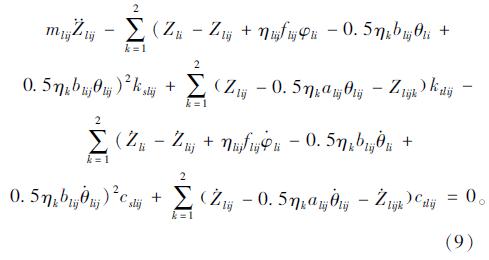
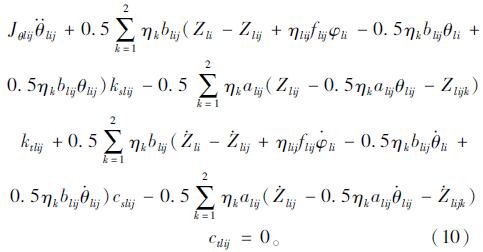
对于本文所选的三轴车,共有9个方程组,其中车体3个,轮对6个。
2.3 桥梁模型的建立及振动方程的求解借助于有限元程序对所求桥梁进行建模处理,获取桥梁的自振模态。对桥梁结构进行离散,获取各阶桥梁振型的模态方程。因此,对应于任意阶振型的模态方程可写成:
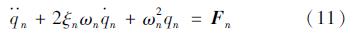
本文利用振型叠加法建立了车桥作用的平衡方程,利用现在成熟的动力学计算方法Newmark-β法逐步积分求得桥梁的动力响应。
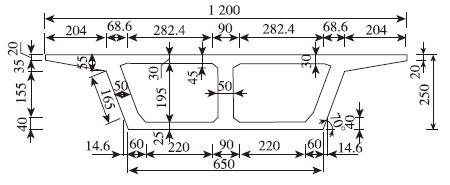
本文以某箱梁作为算例,混凝土采用C50。具体尺寸见图 2。
|
| 图 2 箱梁截面尺寸(单位:cm) Fig. 2 Sectional dimensions of box girder(unit:cm) |
按照箱梁的具体构造,用有限元分析程序Midas建立了跨度为49.92 m的箱梁的有限元模型。混凝土顶底板采用实体单元。具体模型如图 3所示。

|
| 图 3 箱梁模型 Fig. 3 Box girder model |
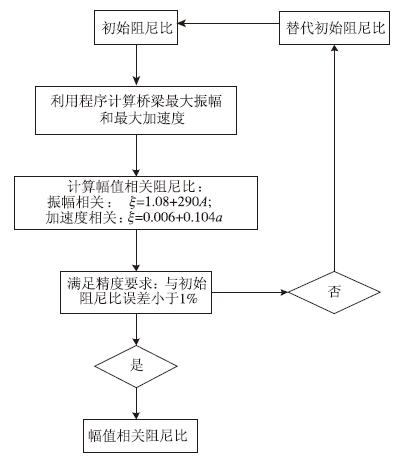
首先输入一个初始阻尼值,根据程序计算的结果,提取各个单元的振幅和加速度数据,选择最大值,分别代入公式(1)和公式(2)中,计算相应的振幅相关和加速度相关阻尼比。当该计算得到的阻尼值与初始阻尼值误差小于1%时,则停止迭代,否则用计算得到的阻尼值代替初始阻尼值,然后按同样的方法计算出在该初始阻尼值下的振幅和加速度数据,继而计算得到相应的幅值相关阻尼值,并将其与初始阻尼值进行比较,直到精度满足要求时停止,迭代过程如图 4所示。
|
| 图 4 阻尼比计算流程图 Fig. 4 Flowchart of damping ratio calculation |
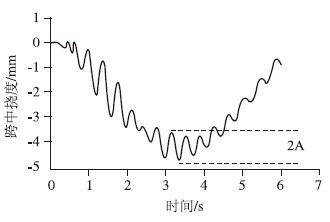
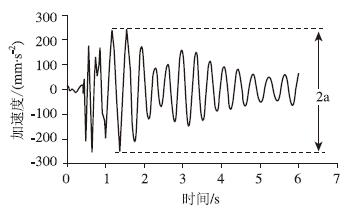
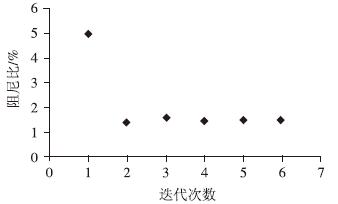
本文振幅幅值和加速度幅值的取值方法如图 5和图 6所示。本文采用初始阻尼比为5%,车速选择30 km/h,车辆选择两辆同向共行,分别计算了振幅相关和加速度相关阻尼比的大小。计算结果见图 7和图 8。
|
| 图 5 振幅取值示意图 Fig. 5 Curve of displacement amplitude |
|
| 图 6 加速度幅值取值示意图 Fig. 6 Curve of acceleration amplitude |
|
| 图 7 振幅阻尼比迭代 Fig. 7 Iteration of displacement damping ratio |
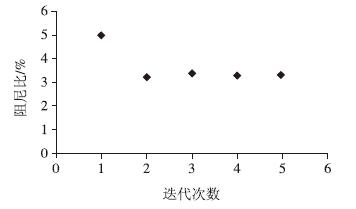
|
| 图 8 加速度阻尼比迭代 Fig. 8 Iteration of acceleration damping ratio |
由图 7和图 8可以看出,振幅相关阻尼比经过6次迭代,加速度相关阻尼比经过5次迭代,能够满足精度的要求。振幅相关的阻尼比最终结果为1.74%,加速度相关的阻尼比最终结果为3.34%。
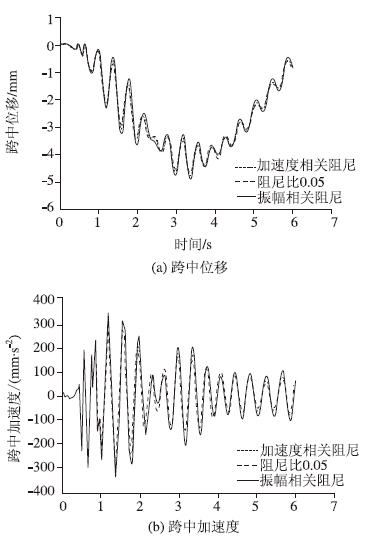
4 幅值相关阻尼下振动计算本文分别利用振幅相关阻尼比、加速度相关阻尼比,和常阻尼比为5%对桥梁的车桥耦合振动响应进行了计算。计算结果如图 9所示。
|
| 图 9 不同阻尼模型下车桥耦合振动计算结果 Fig. 9 Calculation result of vehicle-bridge coupling vibration using different damping modes |
由图 9可以看出,阻尼比取值的不同,对位移响应曲线和加速度响应曲线的趋势没有明显影响,仅对响应的极限值存在影响。阻尼比取值越大,桥梁的振幅和加速度幅值均不同程度的减小。振幅相关阻尼比、加速度相关阻尼比和阻尼比为5%下:理论计算的加速度峰值分别为338,275,223 mm/s2,实际测试的加速峰值为266 mm/s2;理论计算的跨中位移峰值分别为4.826,4.773,4.712 mm。由此可见,利用加速度幅值相关阻尼比计算的结果与实际测试的结果吻合度更高。
5 结论本文开展了幅值相关阻尼比在车桥耦合振动中的应用研究。首先编制了车桥耦合计算程序,利用相关文献提出的振幅相关阻尼比和加速度幅值相关阻尼比的计算方法,结合一座波纹钢腹板简支箱梁,计算了实际桥梁幅值相关阻尼比,并且对比了采用常阻尼比0.05和采用幅值相关阻尼比的车桥耦合振动响应。对比结果发现,采用幅值相关阻尼计算的响应结果小于采用常阻尼比0.05的响应计算结果,其中加速度相关阻尼比的计算结果和实测结果吻合度较高。由于阻尼比的确定困难,使得采用常阻尼比计算的不确定性较大。幅值相关阻尼比能够很好地克服这个缺陷,并且求解的结果有着较高的精度。
| [1] | JTG/T D60—01—2004, 公路桥梁抗风设计规范[S]. JTG/T D60—01—2004, Wind-resistant Design Specifica- tion for Highway Bridge[S]. |
| [2] | JTG/T B02—01—2008, 公路桥梁抗震设计细则[S]. JTG/T B02—01—2008, Guidelines for Seismic Design of Highway Bridges[S]. |
| [3] | GB50011—2010, 建筑抗震设计规范[S]. GB50011—2010, Code for Seismic Design of Building[S]. |
| [4] | Eurocode 8: Design of Structures for Earthquake Resistance[S]. |
| [5] | California Department of Transportation (Caltrans). Seismic Design Criteria (SDC-2010)[S]. Sacramento, Califonia: Caltrans, 2010. |
| [6] | HART G C, VASNDEVAN R. Earthquake Design of Building Damping [J]. Journal of the Structural Division, 1975, 101(1): 185-19. |
| [7] | WEN J, WANG Y F. The Influence of Damping Change on Dynamic Response of Concrete-filled Steel Tubular Arch Bridges[C]// Proceedings of the 4th International Conference on Advances in Steel Structures. Shanghai: Elsevier, 2005, 1675-1680. |
| [8] | DAVENPORT A G, HILL-CARROLL P. Damping in Tall Buildings: Its Variability and Treatment in Design [C]// Proceedings of American Society of Civil Engineers (ASCE) Spring Convention. Seattle: ASCE, 1986: 42-57. |
| [9] | LAGOMARSINO S. Forecast Models for Damping and Vibration Periods of Buildings [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 48(2/3): 221-239. |
| [10] | SUDA K, SATAKE N, ONO J, et al. Damping Properties of Buildings in Japan [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1996, 59(2/3):383-392. |
| [11] | JEARY A P. Damping in Structures [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 72(9/10):345-355. |
| [12] | GLANVILLE M J, KWOK K C S, DENOON R O. Full-scale Damping Measurements of Structures in Australia [J].Journal of Wind Engineering and Industrial Aerodynamics, 1996, 59(2/3):349-364. |
| [13] | LI Q S, FANG J Q, JEARY A P, et al. Evaluation of Wind Effects on a Super Tall Building Based on Full-scale Measurements [J]. |
| [14] | LI Q S, XIAO Y Q, WONG C K, et al. Field Measurements of Typhoon Effects on a Super Tall Building [J]. |
| [15] | LI Q S, XIAO YQ, FU J Y, et al. Full-scale Measurements of Wind Effects on the Jin Mao Building [J]. |
| [16] | RACHEL B, BOBBY S, KIJEWSKI-CORREA T, et al. Full-scale Performance Evaluation of Tall Buildings under Wind [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 104/105/106:88-97. |
| [17] | EYRE R, TILLY G P. Damping Measurements on Steel and Composite Bridges [C]//Proceedings of a Symposium on Dynamic Behaviour of Bridges at the Transport and Road Research Laboratory. Crowthorne, UK: The Transportation Research Board Publications, 1977: 22-39. |
| [18] | TILLY G P. Damping of Highway Bridges: A Review [C]//Proceedings of a Symposium on Dynamic Behaviour of Bridges at the Transport and Road Research Laboratory. Berkshire, UK: The Transportation Research Board Publications, 1977: 1-9. |
| [19] | GREEN M F, CEBON D. Modal Testing of Two Highway Bridges[C]// Proceedings of 11th International Modal Analysis Conference. Kissimme, FL: Wiley, 1993: 838-844. |
| [20] | GREEN R. Dynamic Response of Bridge Superstructures-Ontario Observations [C]// Proceedings of a Symposium on Dynamic Behaviour of Bridges at the Transport and Road Research Laboratory. Berkshire, UK: The Transportation Research Board Publications 1977: 40-55. |
| [21] | BILLING J R. Dynamic Loading and Testing of Bridges in Ontario [J]. Canadian Journal of Chemical Engineering, 1984, 11(4):833-843. |
| [22] | BILLING J R. Dynamic Test of Bridges in Ontario, 1980: Data Capture, Test Procedures and Data Processing, MTC Research and Development Report SRR-82-02[R]. Downsview, Canada: Ontario Ministry of Transportation and Communications, 1982. |
| [23] | CASAS J R. Full-scale Dynamic Testing of the Alamillo Cable-stayed Bridge in Sevilla(Spain) [J]. |
| [24] | MYRVOLL F, KAYNIA A M, HANSEN E. Full-scale Dynamic Performance Testing of the Bridge Structure and the Special Cable Friction Dampers on the Cable-stayed Uddevalla Bridge[C]// 20th IMAC Conference on Structural Dynamics. Los Angeles: Springer, 657-662. |
| [25] | MAGALHÃES F, CUNHA Á, CAETANO E, et al. Damping Estimation Using Free Decays and Ambient Vibration Tests [J]. |
| [26] | REBELO C, DA SILVA L S, RIGUEIRO C, et al. Dynamic Behaviour of Twin Single-span Ballasted Railway Viaducts-Field Measurements and Modal Identification [J]. |
| [27] | VLKER-KAUSTELL M, KAROUMI R. Application of the Continuous Wavelet Transform on the Free Vibrations of a Steel-concrete Composite Railway Bridge [J]. |
| [28] | VLKER-KAUSTELL M, KAROUMI R. Influence of Non-linear Stiffness and Damping on the Train-bridge Resonance of a Simply Supported Railway Bridge [J].Engineering Structures, 2012, 41(8):350-355. |
| [29] | 许士杰. 钢管混凝土肋拱桥自振特性及汽车荷载作用下动力响应的研究[D].北京:北京交通大学, 1999. XU Shi-jie. Study on Natural Vibration Characteristics and Bridge-vehicle Dynamic Interaction of Concrete Filled Steel Tubular Arch Bridges [D]. Beijing: Beijing Jiaotong University, 1999. |
 2015, Vol. 31
2015, Vol. 31
