扩展功能
文章信息
- 杨晓明, 陈永林, 李富斋, 白真宙
- YANG Xiao-ming, CHEN Yong-lin, LI Fu-zhai, BAI Zhen-zhou
- 往复荷载作用后锈蚀钢筋混凝土梁承载力数值模拟
- Numerical Simulation of Load Bearing Capacity of Corroded Reinforced Concrete Beam after Cyclic Loading
- 公路交通科技, 2015, Vol. 31 (5): 81-87
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (5): 81-87
- 10.3969/j.issn.1002-0268.2015.05.014
-
文章历史
- 收稿日期:2014-01-20
2. 中国人民解放军95937部队, 辽宁 阜新 123000
2. Chinese PLA 95937 Troops, Fuxin Liaoning 123000, China
钢筋混凝土材料自投入使用以来,以其受力性能良好、价格低廉等优势被广泛应用于桥梁、海港、高速公路、工业厂房以及民用建筑等之中。但是我们发现,这些结构在使用过程中,因钢筋锈蚀导致的承载力下降问题[1]、往复荷载作用下的疲劳破坏问题[2, 3]以及二者相互耦合作用下的结构安全使用问题[4],给国家和人民带来巨大的经济损失和严重的安全隐患[5, 6, 7]。对于钢筋混凝土结构的使用者和管理者来说,首要关心的是结构的承载力性能,为了能在结构使用过程中及时发出危险预警,需准确获得锈蚀钢筋混凝土构件在经历若干次疲劳荷载作用后的实际承载能力。因此,本文从这一角度出发对锈蚀钢筋混凝土梁在经历若干次疲劳荷载作用后的静载承载力进行数值模拟分析,为承受疲劳荷载的锈蚀钢筋混凝土结构的安全预警提供理论支持。
本文采用ABAQUS有限元软件建立钢筋混凝土梁模型,通过修改钢筋截面面积、屈服强度和极限强度等参数来模拟钢筋锈蚀及往复荷载的影响,分别对不同锈蚀率不同循环次数往复荷载作用后的钢筋混凝土梁进行静力非线性分析,获得其荷载-挠度曲线,并由此分析钢筋锈蚀及往复荷载循环次数对钢筋混凝土梁承载性能的影响规律。
1 数值模拟前处理 1.1 单元选取在ABAQUS有限元软件中,采用C3D8R单元,即八节点六面体线性减缩积分单元来描述混凝土。模拟钢筋采用桁架单元T3D2,它用于模拟其他单元里的加强构件,而钢筋作为埋置在混凝土中的部件,主要起加强混凝土承载能力的作用,因此选用桁架单元T3D2符合实际情况。
1.2 混凝土本构关系的选取在数值模拟中混凝土选用弹塑性损伤模型。在弹塑性损伤模型中:(1)混凝土受拉、受压应力-应变曲线关系采用混凝土规范(GB50010—2010)推荐的单轴受拉、受压应力-应变曲线方程;(2)损伤因子的计算是采用能量等效假设和混凝土规范(GB50010—2010)中单轴受拉、受压应力-应变曲线方程相结合的方法,并假定在受拉、受压峰值应力前无损伤发生,不进行应力、应变和损伤的计算;(3)弹塑性损伤模型中的其他参量根据现有规范、文献和经验取值,如表 1所示。
| 膨胀角/(°) | 偏心率 | 双轴极限抗压 强度/单轴极限抗压强度 | 拉伸子午面和压缩子午面第二应力不变量之比 | 黏聚系数 | |
| 数值 | 30 | 0.1 | 1.160 | 0.667 | 0.005 |
在ABAQUS软件中,钢筋一般采用弹塑性模型进行描述,而常用的弹塑性模型有双直线模型、二斜线模型和三折线模型3种。本文在既体现钢筋在屈服后出现加强硬化现象又考虑以本构关系尽量简单且符合实际的情况下,选用二斜线模型,见式(1):
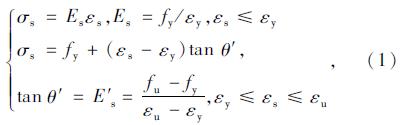
由于钢筋受锈蚀和往复荷载双重破坏因素直接影响钢筋的性能,为了避免分析过于复杂,本文只考虑钢筋在锈蚀和往复荷载作用下性能的变化。描述钢筋性能的主要参数有钢筋截面面积、屈服强度、极限强度和弹性模量等,本文假定弹性模量在整个模拟过程中不受钢筋锈蚀及往复荷载作用的影响。对于钢筋截面面积、屈服强度和极限强度受锈蚀和往复荷载的影响可以根据文献[8, 9, 10, 11, 12]推导得出,如式(2)~式(6)所示,具体推导过程参见文献[13]。
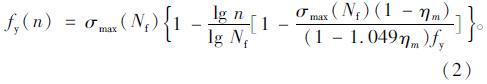
当钢筋质量锈蚀率0%≤ηm<2%时:
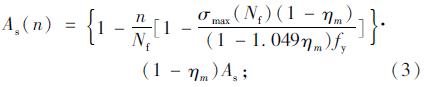
当钢筋质量锈蚀率2%≤ηm≤10%时:
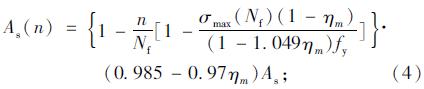
当钢筋质量锈蚀率10%<ηm≤20%时:


上述式中,fy(n)为钢筋剩余屈服强度;fu(n)为钢筋剩余极限强度;fy为钢筋初始屈服强度;σmax(Nf)为钢筋破坏所允许的最大应力;n为往复荷载循环次数;Nf为钢筋疲劳寿命;ηm为钢筋质量锈蚀率;As(n) 为钢筋剩余截面面积;As为钢筋初始截面面积。
2 算例 2.1 模型基本信息算例采用文献[14]中进行锈蚀钢筋混凝土梁弯曲疲劳性能试验的模型梁,其具体尺寸、配筋及加载方式等如图 1所示,其中F为施加荷载,混凝土型号为C30,弹性模量为31.4 GPa,轴心抗拉强度标准值为2.01 MPa,棱柱体抗压强度值为36 MPa,混凝土密度为2 400 kg/m3,泊松比为0.2;受拉钢筋型号为HRB335,弹性模量为201 GPa,密度为7 800 kg/m3,屈服强度为371.02 MPa,极限强度为550.34 MPa,泊松比为0.3;受压钢筋和箍筋型号为HPB235,弹性模量为206 GPa,密度为7 800 kg/m3,屈服强度为361.83 MPa,极限强度为468.19 MPa,泊松比为0.3。
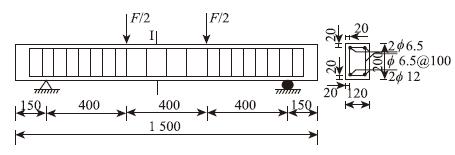
|
| 图1 钢筋混凝土梁设计图 (单位:mm) Fig.1 Design diagram of reinforced concrete beam (unit: mm) |
根据模型的尺寸和配筋形式采用分离式建模方法,建好的钢筋骨架如图 2所示,采用Embedded技术将其埋入混凝土中,使其共同受力及产生变形。建好的钢筋混凝土梁模型如图 3所示。为避免加载点、支座处因应力集中而出现局部破坏,在梁施加荷载处和支座处设置垫板,进行弹性过渡。
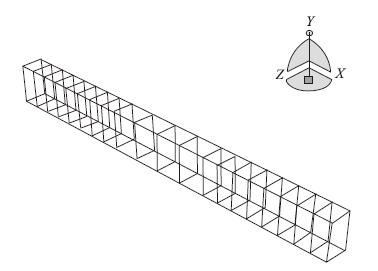
|
| 图2 钢筋骨架模型 Fig.2 Model of reinforcement skeleton |
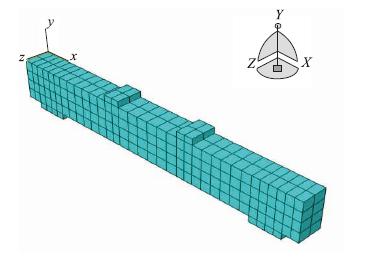
|
| 图3 钢筋混凝土梁模型 Fig.3 Model of reinforced concrete beam |
本文主要针对经历往复荷载后的锈蚀钢筋混凝土梁进行静力非线性分析,以获得其荷载-挠度曲线,并从中得出开裂荷载、屈服荷载和极限荷载等参数。为了验证采用ABAQUS软件进行钢筋混凝土梁承载力数值模拟的可行性,首先进行无锈钢筋混凝土梁静载承载力分析。之后,为了更好地分析钢筋锈蚀与往复荷载作用对钢筋混凝土梁静力承载性能的影响,分别选取质量锈蚀率为0%,3%,5%,8%,10%,13%,15%和循环次数为10,20,30,40,50,60,70,80,90,100万次,两两组合后进行往复荷载后锈蚀钢筋混凝土梁的静力非线性分析,总计70个工况。
3 数值模拟结果分析 3.1 无锈钢筋混凝土梁静载分析根据文献[15]计算出模型的开裂荷载、屈服荷载和极限荷载的理论值和文献[14]提取的试验值与本文的模拟值进行对比分析,如表 2所示。将文献[14]提取试验的荷载-挠度曲线与本文模拟的荷载-挠度曲线进行对比分析,如图 4所示。
| 开裂荷载 | 屈服荷载 | 极限荷载 | ||||||
| 模拟值 | 理论值 | 试验值 | 模拟值 | 理论值 | 试验值 | 模拟值 | 理论值 | 试验值 |
| 13.29 | 10.61 | 15.92 | 66.28 | 61.83 | 74.85 | 76.02 | 67.52 | 82.97 |
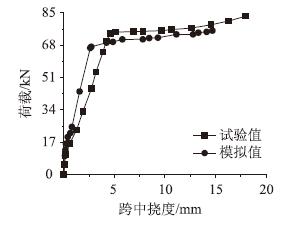
|
| 图4 荷载-挠度对比曲线 Fig.4 Curves of load vs. deflection |
对表 1进行分析可知,本文对文献[14]的模型进行数值模拟得出的开裂荷载值、屈服荷载值及极限荷载值介于文献[15]计算的理论值和文献[14]的试验值之间,且较理论值更接近试验值。从图 4可以看出,当荷载较小时,曲线呈线性增长,梁处于弹性工作阶段;当荷载达到开裂荷载时,荷载-挠度曲线出现第1次明显拐点,其增长速率加快,表明受拉区混凝土开裂;当荷载达到屈服荷载时,荷载-挠度曲线出现第2次明显拐点,表明受拉钢筋屈服;当荷载大于屈服荷载时,荷载-挠度曲线继续增长,但增长速率变慢,表明此时梁处于屈服阶段。从整体上看,两条曲线各阶段都相互接近,比较吻合。综上,通过对数据和曲线图的对比分析,表明采用ABAQUS软件进行钢筋混凝土梁承载力数值模拟是可行的。
3.2 往复荷载作用后锈蚀钢筋混凝土梁承载力分析 3.2.1 理论值比较根据文献[13]中往复荷载作用后锈蚀钢筋混凝土梁承载力的理论计算公式计算出不同锈蚀率和不同循环次数下锈蚀钢筋混凝土梁的承载力值,将其与本文的模拟值进行对比分析。表 3所示为锈蚀率为15%钢筋混凝土梁在不同循环次数往复荷载作用下其屈服荷载的理论值与模拟值。从表 3可以看出,各循环次数下的理论值与试验值都比较接近,由此表明,本文对钢筋锈蚀与往复荷载作用的模拟方法是有效的。
| 循环次数/万次 | 理论值/kN | 模拟值/kN | 误差/% |
| 10 | 31.050 | 31.214 | 0.526 |
| 20 | 30.304 | 30.519 | 0.704 |
| 30 | 29.558 | 30.141 | 1.936 |
| 40 | 28.810 | 29.193 | 1.310 |
| 50 | 28.062 | 28.066 | 0.014 |
| 60 | 27.314 | 27.659 | 1.249 |
| 70 | 26.565 | 26.892 | 1.218 |
| 80 | 25.815 | 26.042 | 0.874 |
| 90 | 25.064 | 25.593 | 2.067 |
| 100 | 24.313 | 24.632 | 1.296 |
本文对不同锈蚀率和不同循环次数往复荷载作用下钢筋混凝土梁在静载作用下的结构响应进行模拟,对各工况下的荷载-挠度曲线进行两类分析。
1)相同锈蚀率
首先分析在相同锈蚀情况下各工况的荷载-挠度曲线变化规律。将同一锈蚀率下各循环次数往复荷载后钢筋混凝土梁的荷载-挠度曲线绘于同一图中,以便于观察荷载-挠度曲线随往复荷载循环次数的变化规律。各锈蚀率下的荷载-挠度曲线基本一致,限于篇幅,本文只给出锈蚀率3%工况的荷载-挠度曲线,如图 5所示。
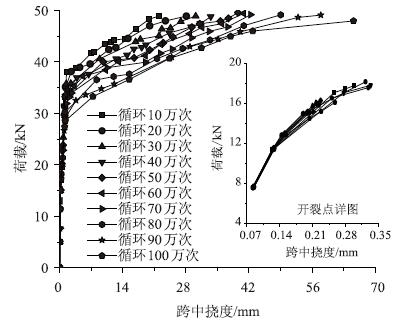
|
| 图 5 锈蚀率3%工况下的荷载-挠度曲线 Fig. 5 Curves of load vs. deflection in corrosion ratio of 3% |
从图 5可以看出:
①当钢筋混凝土梁达到开裂荷载前,荷载-挠度曲线呈线性,此时构件处于弹性工作状态,且荷载-挠度曲线的斜率随着往复荷载的循环次数的增加略有下降,如图 5中小图所示;
②当梁达到开裂荷载时,梁出现第1条裂缝,荷载-挠度曲线出现第1次明显拐点,如图 5中小图所示,拐点后荷载-挠度曲线的斜率降低,其降低程度随循环次数的增加而增大,说明钢筋混凝土梁开裂后刚度有所下降,且下降程度随循环次数的增加而增大;
③随着施加荷载的增加,受拉钢筋开始屈服,荷载-挠度曲线出现第2次明显拐点,且屈服荷载随循环次数的增加而明显降低;
④钢筋混凝土梁进入屈服阶段以后,荷载-挠度曲线表现为非线性,梁体挠度迅速增长直到极限状态,而且在各锈蚀率下,随着循环次数的增大,梁体的极限挠度显著增大。
(2)相同循环次数
其次分析在相同循环次数的往复荷载下各工况的荷载-挠度曲线变化规律。将同一循环次数下各锈蚀率钢筋混凝土梁的荷载-挠度曲线绘于同一图中,以便于观察荷载-挠度曲线随锈蚀率的变化规律。各循环次数下的荷载-挠度曲线基本一致,限于篇幅,本文只给出循环次数为30万次工况的荷载-挠度曲线,如图 6所示。
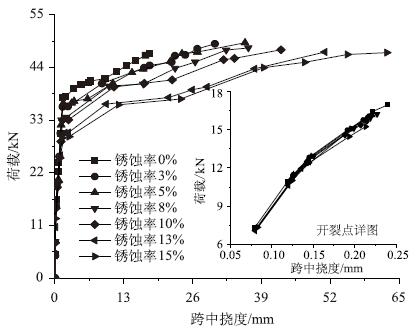
|
| 图 6 循环30万次工况荷载-挠度曲线 Fig. 6 Curves of load vs. deflection after 300 000 time of cyclic loading |
从图 6可以看出:
(1)当钢筋混凝土梁达到开裂荷载前,荷载-挠度曲线呈线性,此时构件处于弹性工作状态,且荷载-挠度曲线的斜率随着锈蚀率的增加略有下降,如图 6中小图所示;
(2)当梁达到开裂荷载时,荷载-挠度曲线出现第1次明显拐点,如图 6中小图所示,拐点后荷载-挠度曲线的斜率降低,其降低程度随锈蚀率的增加而增大;
(3)随着施加荷载的增加,受拉钢筋开始屈服,荷载-挠度曲线出现第2次明显拐点,且屈服荷载随锈蚀率的增加而明显降低;
(4)钢筋混凝土梁进入屈服阶段以后,荷载-挠度曲线表现为非线性,梁体挠度迅速增长直到极限状态,而且在各循环次数下,随着锈蚀率的增大,梁体的极限挠度显著增大。
3.2.3 影响因素分析钢筋混凝土梁在承受往复荷载和钢筋锈蚀双重破坏作用下,其结构性能会显著退化,其中最为关键的结构性能为屈服荷载和极限挠度,二者对于确保结构的安全使用和保证损失最小化有重要意义。以下将分别研究钢筋锈蚀、往复荷载以及二者共同作用情况下,往复荷载作用后锈蚀钢筋混凝土梁的屈服荷载和极限挠度的变化规律。
(1)钢筋锈蚀
为了更好地分析钢筋锈蚀对钢筋混凝土梁的屈服荷载与极限挠度的影响,将每种工况下的屈服荷载与极限挠度提取出来,分别绘制在一幅图中,如图 7、图 8所示,其中横轴为钢筋锈蚀率,纵轴分别为屈服荷载与极限挠度。从图 7中可以看出,随着钢筋锈蚀率的增加,当往复循环次数较少的时候,钢筋混凝土梁的屈服荷载基本呈线性下降;当循环次数较大时,屈服荷载开始呈线性下降,锈蚀率超过10%时,屈服荷载下降速度加快。其主要原因在于高锈蚀率高循环次数下,钢筋锈蚀与往复荷载的耦合作用更加显著,以至于屈服强度迅速下降。从图 8中可以看出,钢筋混凝土梁的极限挠度随着钢筋锈蚀率的增长而加大,但二者呈非线性变化,当锈蚀率小于5%时,极限挠度增长较快,锈蚀率处于5%~8%之间时,极限挠度增长速度变缓,锈蚀率超过8%时,极限挠度增长加快。
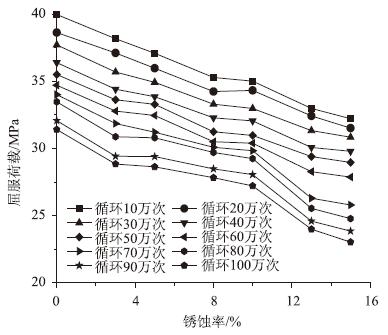
|
| 图 7 屈服荷载-锈蚀率曲线 Fig. 7 Curves of yield load vs. corrosion ratio |
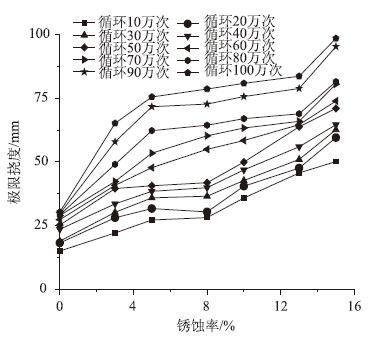
|
| 图 8 极限挠度-锈蚀率曲线 Fig. 8 Curves of ultimate deflection vs. corrosion ratio |
(2)往复荷载循环次数
分析往复荷载循环次数对钢筋混凝土梁的屈服荷载与极限挠度的影响时,同样将每种工况下的屈服荷载与极限挠度提取出来,分别绘制在一幅图中,如图 9与图 10所示,其中横轴为往复荷载循环次数,纵轴分别为屈服荷载与极限挠度。从图 9中可以看出,随着往复荷载循环次数的增加,钢筋混凝土梁的屈服荷载也随之下降,二者基本呈线性关系,此线性关系在不同锈蚀率情况下均有体现。从图 10中可以看出,钢筋混凝土梁的极限挠度随着往复荷载循环次数的增长而增长,二者基本呈线性变化,但变化趋势有所不同,当无锈蚀时,极限挠度随循环次数增长较慢,当出现锈蚀后,极限挠度增长加快。
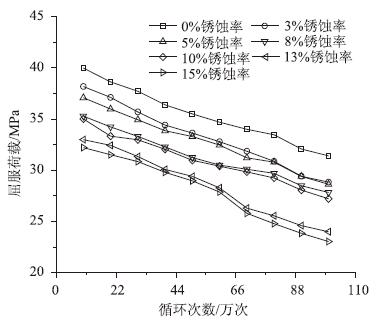
|
| 图 9 屈服荷载-循环次数曲线 Fig. 9 Curves of yield load vs. cyclic times |
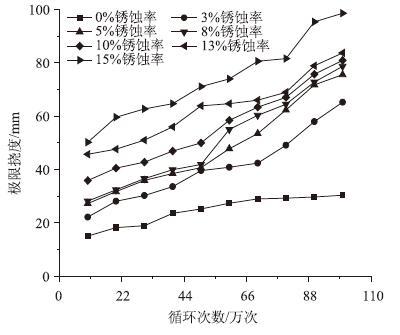
|
| 图 10 极限挠度-循环次数曲线 Fig. 10 Curves of ultimate deflection vs. cyclic times |
(3)二者共同作用
在分析钢筋锈蚀与往复荷载循环次数对钢筋混凝土梁的屈服荷载与极限挠度影响的基础上,进一步分析二者共同作用下钢筋混凝土梁的屈服荷载与极限挠度变化规律。为此,将每种工况下的屈服荷载与极限挠度同锈蚀率及循环次数绘制三维曲面图,如图 11、图 12所示,其中两个横轴为锈蚀率与往复荷载循环次数,纵轴分别为屈服荷载与极限挠度。从图 11中可以看出,随着往复荷载循环次数及锈蚀率的增加,钢筋混凝土梁的屈服荷载也均匀下降,二者对屈服荷载的影响程度比较相当,当往复荷载循环次数及锈蚀率较大时,屈服荷载出现陡降现象,说明此时二者耦合作用比较显著。从图 12中可以看出,随着往复荷载循环次数及锈蚀率的增加,钢筋混凝土梁的极限挠度不断增长,但二者的影响程度有所不同,锈蚀率的影响要高于往复荷载循环次数的影响,特别是当循环次数较大时,此现象更加明显。
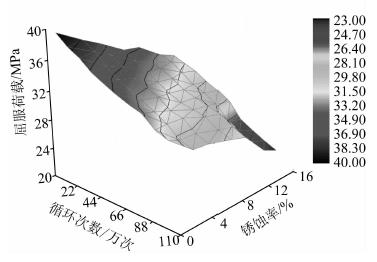
|
| 图 11 屈服荷载-循环次数-锈蚀率曲线 Fig. 11 Curved surface of yield load vs. cyclic times and corrosion ratio |
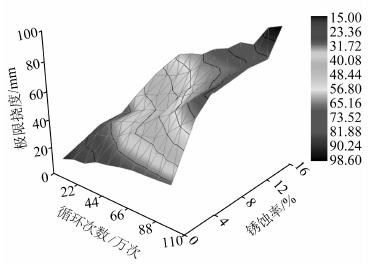
|
| 图 12 极限挠度-循环次数-锈蚀率曲线 Fig. 12 Curved surface of ultimate deflection vs. cyclic times and corrosion ratio |
本文采用ABAQUS软件对往复荷载作用后锈蚀钢筋混凝土梁的静力加载过程进行数值模拟,通过分析不同锈蚀率不同往复荷载循环次数工况下的数值模拟结果,得出以下结论:
(1)采用ABAQUS模拟的无锈钢筋混凝土梁静载承载力结果与试验结果及理论结果比较吻合,表明使用ABAQUS软件进行钢筋混凝土梁数值模拟是可行的;
(2)往复荷载作用后锈蚀钢筋混凝土梁承载力数值模拟结果与理论公式的计算结果基本吻合,相对误差小于5%,说明数值模拟中采用的往复荷载作用后锈蚀钢筋本构关系是可行有效的;
(3)钢筋锈蚀及往复荷载循环次数会影响钢筋混凝土梁的荷载-挠度曲线,在屈服前,钢筋锈蚀率及往复荷载循环次数越大,荷载-挠度曲线的斜率越小,同时,钢筋锈蚀率及往复荷载循环次数越大,钢筋混凝土梁的屈服荷载越小,极限挠度越大;
(4)往复荷载作用后锈蚀钢筋混凝土梁的屈服荷载随钢筋锈蚀率及往复荷载循环次数的增加基本呈线性下降,二者对屈服荷载影响程度比较接近,但当往复荷载循环次数及锈蚀率较大时,屈服荷载出现陡降现象,此时二者耦合作用比较显著;
(5)往复荷载作用后锈蚀钢筋混凝土梁的极限挠度随钢筋锈蚀率的增加非线性增大,随往复荷载循环次数的增加基本线性增大,但锈蚀率的影响要高于往复荷载循环次数的影响,特别是当循环次数较大时,此现象更加明显。
| [1] | 张伟平, 顾祥林, 金贤玉, 等. 混凝土中钢筋锈蚀机理及锈蚀钢筋力学性能研究[J]. 建筑结构学报, 2010, 31(增1): 327-332. ZHANG Wei-ping, GU Xiang-lin, JIN Xian-yu, et al. Study on Corrosion Mechanism of Steel Bars in Concrete and Mechanical Performance of Corroded Steel Bars[J]. Journal of Building Structures, 2010, 31 (S1):327-332. |
| [2] | 吴瑾, 黄杰. 低锈蚀率钢筋混凝土梁疲劳性能试验研究[J]. 工业建筑, 2009, 39(5):65-67. WU Jin, HUANG Jie. Research on Fatigue Behavior of Concrete Beams with Slight Corrosion Reinforcement[J]. Industrial Construction, 2009, 39(5):65-67. |
| [3] | 葛若东, 梁进修, 王磊. 碳纤维加固锈蚀混凝土梁短期疲劳性能研究[J]. 工业建筑, 2012, 42(6):72-76. GE Ruo-dong, LIANG Jin-xiu, WANG Lei. The Analysis of Flexural Behavior of Corroded RC Beams Strengthened with CFRP under Fatigue Loads[J]. Industrial Construction, 2012, 42(6):72-76. |
| [4] | 易伟建, 孙晓东. 锈蚀钢筋混凝土梁疲劳性能试验研究[J]. 土木工程学报, 2007, 40(3):6-10. YI Wei-jian, SUN Xiao-dong. Experimental Investigation on the Fatigue Behavior of Corroded RC Beams[J]. China Civil Engineering Journal, 2007, 40(3):6-10. |
| [5] | LI C Q, MELCHERS R E. Time-dependent Risk Assessment of Structural Deterioration Caused by Reinforcement Corrosion[J]. ACI Structural Journal, 2005, 102(5):754-764. |
| [6] | CORONELLI D, GAMBAROVA P. Structural Assessment of Corroded Reinforced Concrete Beams:Modeling Guidelines[J]. |
| [7] | 唐国斌, 王统宁, 项贻强. 混凝土桥梁服役过程中荷载与锈蚀的耦合作用[J]. 公路交通科技, 2013, 30(11):62-67. TANG Guo-bin, WANG Tong-ning, XIANG Yi-qiang. Couple Effect of Loading and Corrosion of Concrete Bridge in Service Life[J]. Journal of Highway and Transportation Research and Development, 2013, 30(11):62-67. |
| [8] | 王晓刚, 顾祥林, 张伟平. 锈蚀钢筋混凝土梁抗弯性能数值模拟[J]. 建筑科学与工程学报, 2009, 26(1):49-54. WANG Xiao-gang, GU Xiang-lin, ZHANG Wei-ping. Numerical Simulation of Flexural Behavior of Corroded Reinforced Concrete Beams[J]. Journal of Architecture and Civil Engineering, 2009, 26(1):49-54. |
| [9] | 王雪慧, 钟铁毅. 混凝土中锈蚀钢筋截面损失率与重量损失率的关系[J]. 建材技术与应用, 2005, 26 (1):4-6. WANG Xue-hui, ZHONG Tie-yi. Relation between the Loss Coefficient of the Corroded Rebar's Cross-section in Concrete and that of Its Weight[J]. Research & Application of Building Materials, 2005, 26 (1):4-6. |
| [10] | 朱劲松, 朱先存. 钢筋混凝土桥梁疲劳累积损伤失效过程简化分析方法[J]. 工程力学, 2012, 29(5):107-114, 121.ZHU Jinsong, ZHU Xiancun. Study on Simplified Method for the Analysis of Fatigue Failure Process of RC Bridges[J]. Engineering Mechanics, 2012, 29(5):107-114, 121. |
| [11] | 李俊, 吴瑾. 钢筋混凝土结构腐蚀疲劳劣化过程的动态寿命评估[J]. 桥梁建设, 2012, 42(4):34-38.LI Jun, WU Jin. Dynamic Life Assessment of RC Structures in Process of Coupled Corrosion and Fatigue Deterioration[J]. Bridge Construction, 2012, 42(4):34-38. |
| [12] | 郝海霞, 张建仁, 彭晖, 等. 锈蚀变形钢筋混凝土受弯构件的受力性能试验研究[J]. 公路交通科技, 2010, 27(10):58-65.HAO Haixia, ZHANG Jianren, PENG Hui, et al. Experimental Study on Mechanical Behavior of Reinforced Concrete Flexural Beam with Corroded Deformed Bars[J]. Journal of Highway and Transportation Research and Development, 2010, 27(10):58-65. |
| [13] | 李富斋. 往复荷载作用后锈蚀钢筋混凝土梁承载力研究 [D]. 阜新:辽宁工程技术大学, 2014.LI Fuzhai. Research on Load Bearing Capacity of Corroded Reinforced Concrete Beam after Reciprocating Load [D]. Fuxin: Liaoning Technical University, 2014. |
| [14] | 李士彬. 锈蚀钢筋混凝土梁的弯曲疲劳性能及寿命预测[D]. 上海:同济大学, 2007.LI Shibin. Flexural Fatigue Behavior and Life Prediction of Corroded Reinforced Concrete Beams[D]. Shanghai:Tongji University, 2007. |
| [15] | 顾祥林. 混凝土结构基本原理[M]. 上海:同济大学出版社, 2004:96-101.GU Xianglin. Basic Principle of Concrete Structure[M]. Shanghai:Tongji University Press, 2004:96-101. |
 2015, Vol. 31
2015, Vol. 31
