扩展功能
文章信息
- 黄新艺, 杨宁, 卓卫东, 魏祥湘
- HUANG Xin-yi, YANG Ning, ZHUO Wei-dong, WEI Xiang-xiang
- 不平度下曲线箱梁桥冲击系数的参数相关性
- Parameter Correlation of Impact Factors of Curved Box-girder Bridges under Roughness Condition
- 公路交通科技, 2015, Vol. 31 (5): 75-80
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (5): 75-80
- 10.3969/j.issn.1002-0268.2015.05.013
-
文章历史
- 收稿日期:2014-06-24
在公路桥梁设计规范中,用冲击系数μ来反映汽车对桥梁产生的动力效应,从而保证桥梁的安全使用。目前,加拿大、美国、日本、法国等国家的相关标准规定都将冲击系数定义为结构基频的函数。我国经过大量的实测和统计分析,也在2004年对桥梁设计规范进行了修订,将冲击系数μ和结构的基频联系起来[1],更为合理和科学地反映了冲击系数的本质。鲍卫刚[2]引入路况系数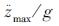 (车体振动的最大竖向加速度和重力加速度的比值)来反映路面的行车条件,研究了车辆作用下桥梁冲击力的取值方法。文献[3]指出了桥面状况系数也是汽车对桥梁冲击另一个极重要因素。桥面不平度是车桥耦合振动的主要激励源,文献[4]通过对实际线路不平度的测量和实桥动力分析结果,指出了应对采用不同不平度的计算结果进行统计分析,以确定车桥动力响应的最不利状态。研究表明:连续梁桥同一位置处的挠度冲击系数总是大于弯矩冲击系数,且随着跨径的增大有减小的趋势[5];多跨连续梁桥边跨和中跨的冲击系数差异很大,桥梁应考虑采用不同的冲击系数[6]。
(车体振动的最大竖向加速度和重力加速度的比值)来反映路面的行车条件,研究了车辆作用下桥梁冲击力的取值方法。文献[3]指出了桥面状况系数也是汽车对桥梁冲击另一个极重要因素。桥面不平度是车桥耦合振动的主要激励源,文献[4]通过对实际线路不平度的测量和实桥动力分析结果,指出了应对采用不同不平度的计算结果进行统计分析,以确定车桥动力响应的最不利状态。研究表明:连续梁桥同一位置处的挠度冲击系数总是大于弯矩冲击系数,且随着跨径的增大有减小的趋势[5];多跨连续梁桥边跨和中跨的冲击系数差异很大,桥梁应考虑采用不同的冲击系数[6]。
在定义冲击系数理论公式时参数的选择方面,早期的美国桥梁设计规范[7]将曲线梁桥的冲击系数定义为桥跨长度的函数。Khaled等[8, 9]在对组合箱梁曲线梁桥的研究中指出了冲击系数与圆心角φ之间存在密切的关系。C.P.Heins教授的研究认为冲击系数是圆心角的函数,且可区分成弯矩冲击系数和扭转冲击系数等情况。加拿大安大略省公路桥梁设计规范(简称OHBDC)[10]则采用了综合影响系数Lφ/b(b为桥面的半宽,L为桥跨长度)来作为判断是否可以按直线梁桥进行计算的条件,该参数反映了跨长/宽度比和圆心角两个参数的综合影响。根据大量的试验结果OHBDC[11]将桥梁的冲击系数定义为结构的竖向弯曲振动基频f1的函数,此外,文献[12]指出了主梁的弯扭刚度比k=EI/GId对曲线梁桥结构的受力状态和变形状态有直接的关系。日本的小西一郎[13]在其著作中则提出了以桥梁跨度为参数的冲击系数计算公式,同时考虑了车辆加载半径和桥梁中心曲率半径之比的影响。
鉴于以上原因和我国现行规范对曲线梁桥冲击系数计算方法规定上存在的不足,本文将通过大量的混凝土连续曲线桥梁实例分析结果,对各种不平度下的冲击系数与各个参数之间的相关性进行分析研究,为冲击系数计算公式参变量的选择提供理论依据。
1 冲击系数的定义桥梁结构在汽车荷载作用下位移冲击系数和内力冲击系数由式(1)分别定义[8]:
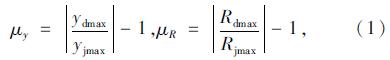
对于常见的曲线箱形梁桥而言,杆件系统的截面主轴和作用的荷载通常不再同一个平面内,因而其振动属于空间振动问题,所以需要选用空间梁单元对结构进行离散。为了更好地考虑翘曲和扭转效应的影响,曲线箱梁桥的模型采用三梁式模型[14]进行离散,车桥动力相互作用的运动方程可以表示为:
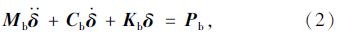
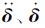 和δ分别为总体加速度、速度和位移向量;Pb为车桥动力相互作用产生的总体外荷载向量。文中桥梁结构的阻尼采用Rayleigh阻尼模式。
2.2 车辆模型
和δ分别为总体加速度、速度和位移向量;Pb为车桥动力相互作用产生的总体外荷载向量。文中桥梁结构的阻尼采用Rayleigh阻尼模式。
2.2 车辆模型
本文模型考虑了车辆竖向、横向振动和绕3个坐标轴方向的旋转振动,比较全面地模拟了车辆自身的振动特性,模型共包含12个广义自由度,车辆的简化模型见图 1。采用拉格朗日方程建立车辆的振动方程,详细的过程及车辆参数参见文献[15]。分析过程中假定车辆沿着与桥梁中心线平行的路线行驶,车辆模型每一个集中质量的离心力水平作用于各自的质心处。
2.3 车桥动力相互作用力假定汽车运行通过桥梁时,车轮与桥面始终保持接触,利用车轮与桥面接触点间的力与位移协调条件,可得到各车轮对桥梁的动力荷载[16]:
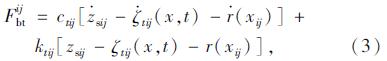

|
| 图1 车辆计算模型简图 Fig.1 Sketch of vehicle calculation model |
桥面不平度可假定为满足零均值的稳态高斯随机过程,常用功率谱密度函数来表述。对功率谱密度函数采用傅立叶逆变换,得到了用三角级数表示的桥面不平度函数为[17]:
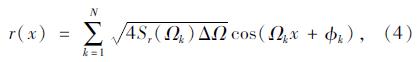
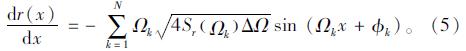
分析过程中考虑到桥面不平度在桥面横向上的差异,选取两个不同的k值,对应于车辆的内侧和外侧车轮与桥面的接触点分别按上述方法生成两组不同的桥面不平度序列。
2 计算参数取值互通式立体交叉中的曲线梁桥不同曲线半径的最大行驶速度参考路线设计的有关规定取值[19],见表 1,考虑到存在超速行驶的可能性较大,在设计车速的基础上均给予适当提高。分析中考虑了桥面不平度的影响,桥面平度系数的取值分别为A级(很好),α-=0.18×10-6m3/circle;B级(好),α-=0.62×10-6m3/circle;C级(一般),α-=2.5×10-6m3/circle;D级(较差),α-=10×10-6 m3/circle。
| 匝道设计行车速度/(km·h-1) | 80 | 60 | 50 | 40 | 35 | 30 | |
| 圆曲线最小半径/m | 一般值 | 280 | 150 | 100 | 60 | 40 | 30 |
| 极限值 | 230 | 120 | 80 | 45 | 35 | 25 | |
表 2中选取了多座不同跨度、不同半径、不同支承和截面形式的混凝土连续曲线梁桥实例进行分析,对于同一种类型的截面通过改变曲率半径来改变曲线梁桥的圆心角,考虑最一般的情况,假定车辆是匀速行驶的。由于多跨连续曲线梁桥的计算工作量较大,选取5个桥面不平度样本与各个桥梁算例组成随机样本对进行计算,采用样本均值作为结果的代表值,考虑桥面不平度的影响,采用分离迭代法对各座算例进行车桥耦合振动的包络分析,找出各桥梁在设计车速范围内的最大动力效应。桥梁算例的基本资料见表 2,动力特性及冲击系数的分析结果详见文献[15]中的内容,有关计算结果在此不再详细列出。
| 桥例 | 桥梁结构主要参数 | ||||
| 桥长L/m | 宽度B/m | 半径R/m | 抗弯惯性矩/m4 | 抗扭惯性矩/m4 | |
| 桥例1 | 120 | 6.6 | 45 | 0.707 | 1.686 |
| 120 | 6.6 | 92 | 0.707 | 1.686 | |
| 120 | 6.6 | 120 | 0.707 | 1.686 | |
| 桥例2 | 80.0 | 8.0 | 76 | 2.883 | 6.146 |
| 桥例3 | 58.5 | 9.0 | 36 | 0.641 | 1.732 |
| 58.5 | 9.0 | 60 | 0.641 | 1.732 | |
| 58.5 | 9.0 | 100 | 0.641 | 1.732 | |
| 桥例4 | 180 | 10.9 | 80 | 8.603 | 11.210 |
| 180 | 10.9 | 130 | 8.603 | 11.210 | |
| 桥例5 | 72 | 8.5 | 25 | 0.496 | 1.338 |
| 72 | 8.5 | 60 | 0.496 | 1.338 | |
| 72 | 8.5 | 100 | 0.496 | 1.338 | |
| 桥例6 | 165 | 12.0 | 200 | 8.198 | 14.621 |
| 桥例7 | 160 | 10.0 | 100 | 10.526 | 20.323 |
| 桥例8 | 120 | 9.0 | 35 | 2.390 | 5.530 |
| 120 | 9.0 | 100 | 2.390 | 5.530 | |
| 桥例9 | 90 | 8.0 | 60 | 1.373 | 2.941 |
| 90 | 8.0 | 150 | 1.373 | 2.941 | |
| 桥例10 | 80 | 8.5 | 35 | 0.607 | 1.148 |
| 80 | 8.5 | 60 | 0.607 | 1.148 | |
| 80 | 8.5 | 160 | 0.607 | 1.148 | |
| 桥例11 | 126 | 15.4 | 120 | 7.039 | 15.070 |
| 126 | 15.4 | 250 | 7.039 | 15.070 | |
| 桥例12 | 100 | 12.0 | 120 | 3.523 | 9.526 |
| 100 | 12.0 | 230 | 3.523 | 9.526 | |
| 桥例13 | 91 | 10.0 | 90 | 4.213 | 8.093 |
| 91 | 10.0 | 150 | 4.213 | 8.093 | |
在前人研究的基础上[8, 9, 10, 12, 13, 15],选取圆心角φ(φ=L/R)、弯扭刚度比(k=EI/GId)、综合影响系数Lφ/B(B为桥面宽度)和弯曲振动基频f1,4个关键参数,通过计算相关系数r来反映两个变量之间关系的密切程度。相关系数由下式计算[20]:
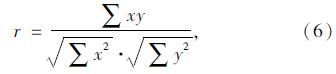

根据式(6)和式(7)分别给出了各种不平度等级(A级,B级,C级,D级)下曲线梁桥的冲击系数与各个选择变量之间的相关性分析结果。
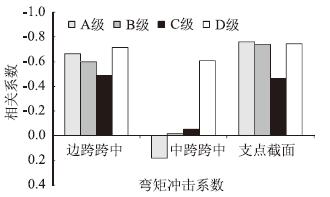
由表 3和图 2可以看出,各种不平度等级下曲线梁桥的弯矩、扭矩、剪力、位移和支座反力的冲击系数除中跨的跨中断面外,与结构的竖向弯曲振动基频之间基本呈负相关,相关系数随着不平度等级的变化有着较明显的改变,但始终都保持较好的相关性。
| 不平度等级 | A级 | B级 | C级 | D级 | |
| 弯矩冲击系数 | 边跨跨中 | -0.664 | -0.597 | -0.485 | -0.715 |
| 中跨跨中 | 0.179 | -0.016 | -0.054 | -0.610 | |
| 支点 | -0.763 | -0.743 | -0.461 | -0.745 | |
| 扭矩冲击系数 | 边跨跨中 | -0.321 | -0.138 | -0.293 | -0.220 |
| 中跨跨中 | 0.238 | 0.014 | 0.002 | -0.461 | |
| 支点 | -0.405 | -0.580 | -0.642 | -0.312 | |
| 剪力冲击系数 | 边跨跨中 | -0.290 | -0.417 | -0.433 | -0.443 |
| 中跨跨中 | 0.242 | 0.099 | 0.174 | -0.588 | |
| 支点 | -0.412 | -0.751 | -0.425 | -0.756 | |
| 位移冲击系数 | -0.735 | -0.876 | -0.489 | -0.764 | |
| 反力冲击系数 | -0.664 | -0.530 | -0.576 | -0.789 | |
|
| 图 2 不同断面弯矩冲击系数与基频间的相关系数 Fig. 2 Correlation coefficients of bending moment impact factor to fundamental frequency at different sections |
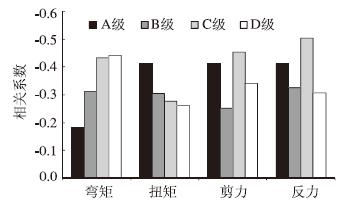
通过表 4和图 3中的结果可知,各种不平度等级下,曲线梁桥的各冲击系数和圆心角φ之间也基本呈负相关关系,相关系数随着不平度等级的增加呈增大的变化规律,支点截面的内力、位移和反力的冲击系数与弯扭刚度比的相关性较其他截面大,但除极个别位置外,相关系数值总体上均小于0.5。
| 不平度等级 | A级 | B级 | C级 | D级 | |
| 弯矩冲击系数 | 边跨跨中 | -0.133 | -0.234 | -0.376 | -0.400 |
| 中跨跨中 | 0.069 | -0.014 | -0.031 | -0.307 | |
| 支点 | -0.182 | -0.311 | -0.433 | -0.443 | |
| 扭矩冲击系数 | 边跨跨中 | 0.059 | 0.006 | -0.167 | -0.094 |
| 中跨跨中 | 0.110 | 0.026 | -0.022 | -0.543 | |
| 支点 | -0.413 | -0.305 | -0.278 | -0.262 | |
| 剪力冲击系数 | 边跨跨中 | -0.024 | -0.179 | -0.372 | -0.498 |
| 中跨跨中 | 0.063 | 0.001 | 0.064 | -0.050 | |
| 支点 | -0.413 | -0.251 | -0.454 | -0.342 | |
| 位移冲击系数 | -0.120 | -0.317 | -0.334 | -0.277 | |
| 反力冲击系数 | -0.412 | -0.325 | -0.503 | -0.306 | |
|
| 图 3 支点截面各冲击系数与基频间的相关系数 Fig. 3 Correlation coefficient of impact factor to fundamental frequency at pivot section |
表 5中的数据表明,各种不平度等级下,冲击系数与主梁的弯扭刚度比k=EI/GId之间基本呈正相关变化,相关系数的变化没有明显的规律可循,但相关系数的值总体上均很小,说明两者之间的相关性很小。
| 不平度等级 | A级 | B级 | C级 | D级 | |
| 弯矩冲击系数 | 边跨跨中 | 0.149 | 0.019 | -0.173 | 0.061 |
| 中跨跨中 | 0.068 | 0.076 | 0.077 | -0.051 | |
| 支点 | 0.179 | 0.149 | 0.175 | 0.187 | |
| 扭矩冲击系数 | 边跨跨中 | -0.002 | -0.031 | -0.063 | -0.043 |
| 中跨跨中 | 0.003 | 0.110 | 0.149 | -0.202 | |
| 支点 | 0.029 | 0.149 | 0.083 | 0.018 | |
| 剪力冲击系数 | 边跨跨中 | -0.015 | -0.166 | -0.047 | -0.016 |
| 中跨跨中 | 0.016 | 0.069 | 0.190 | 0.034 | |
| 支点 | -0.035 | 0.246 | -0.151 | 0.160 | |
| 位移冲击系数 | 0.245 | 0.306 | 0.086 | 0.208 | |
| 反力冲击系数 | 0.248 | 0.200 | 0.076 | 0.221 | |
表 6中的数据表明,各种不平度等级下,各冲击系数与综合影响系数Lφ/B之间基本呈负相关的形式,部分截面的冲击系数变化规律和圆心角类似,各相关系数的大小与冲击系数和圆心角之间的相关系数较接近,表明跨宽比对相关系数的影响较小。
| 不平度等级 | A级 | B级 | C级 | D级 | |
| 弯矩冲击系数 | 边跨跨中 | -0.176 | -0.252 | -0.347 | -0.314 |
| 中跨跨中 | 0.082 | 0.022 | 0.039 | -0.253 | |
| 支点 | -0.179 | -0.199 | -0.300 | -0.343 | |
| 扭矩冲击系数 | 边跨跨中 | 0.167 | 0.039 | -0.145 | -0.032 |
| 中跨跨中 | 0.158 | 0.074 | 0.037 | -0.533 | |
| 支点 | -0.331 | -0.226 | -0.210 | -0.203 | |
| 剪力冲击系数 | 边跨跨中 | -0.279 | -0.400 | -0.485 | -0.480 |
| 中跨跨中 | 0.064 | 0.015 | 0.176 | 0.001 | |
| 支点 | -0.441 | -0.170 | -0.408 | -0.215 | |
| 位移冲击系数 | -0.103 | -0.187 | -0.251 | -0.155 | |
| 反力冲击系数 | -0.321 | -0.259 | -0.431 | -0.165 | |
|
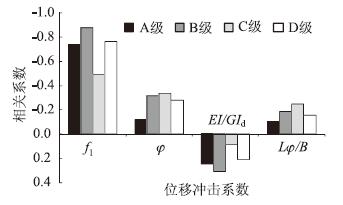
| 图 4 位移冲击系数与不同参数间的相关系数 Fig. 4 Correlation coefficients of displacement impact factor to different parameters |
通过对表 3~表 6和图 4的结果对比可知:
(1)曲线箱梁桥各冲击系数与竖向弯曲振动基频之间的相关系数明显高于与圆心角、弯扭刚度比和综合影响系数Lφ/B之间的相关系数,说明冲击系数与主梁的竖向弯曲振动基频之间存在密切关系;相关系数随着不平度的改变均有较明显的变化,各相关系数均小于1,说明冲击系数与各个参数之间为非线性相关。
(2)除主梁各中跨跨中截面外,其他位置的弯矩、扭矩、剪力、挠度和反力冲击系数与竖向弯曲振动基频、圆心角和综合影响系数Lφ/B均呈负相关,即冲击系数随着这些参数的增大而减小。
(3)主梁的各项内力、挠度冲击系数与弯扭刚度比之间呈正相关,即随着弯扭刚度比的增大结构的冲击系数增大。因此,提高主梁的抗扭刚度可在一定程度上减小车辆对桥梁的冲击效应。
(4)各控制截面的内力和位移冲击系数与结构竖向弯曲振动基频之间呈现出较理想的相关性,冲击系数随着结构竖向弯曲振动基频的增大而减小,随着不平度等级的改变各相关系数的变化较大。因此,宜将冲击系数根据不同的桥面不平度等级定义为竖向弯曲振动基频f1的函数。
| [1] | 张向东, 刘家顺.循环荷载作用下风积土累积塑性变形试验研究[J]. 公路交通科技, 2014, 31(3): 18-25. ZHANG Xiang-dong, LIU Jia-shun. Experimental Study on Cumulative Plastic Deformation of Aeolian Soil under Cyclic Loading[J]. Journal of Highway and Transp-ortation Research and Development, 2014, 31(3): 18-25. |
| [2] | 张向东, 李旭, 刘家顺, 等.动荷载作用下风积土路基振陷变形[J].公路交通科技, 2011, 28(12): 39-43. ZHANG Xiang-dong, LI Xu, LIU Jia-shun, et al. Vibration Excited Subsidence of Aeolian Subsoil under Dynamic Load[J]. Journal of Highway and Transportation Research and Development, 2011, 28(12): 39-43. |
| [3] | 张向东, 刘家顺. 风积土震陷变形试验研究[J].土壤通报, 2014, 45(1): 66-71. ZHANG Xiang-dong, LIU Jia-shun. Experimental Study on Subsidence Deformation of Aeolian Soil under Seismic Loads[J]. Chinese Journal of Soil Science, 2014, 45(1): 66-71. |
| [4] | 张树光, 张向东, 易富. 辽西地区冻风积土水分迁移特征的研究[J].岩土力学, 2006, 27(3):418-422. ZHANG Shu-guang, ZHANG Xiang-dong, YI Fu. Study on Moisture Transfer of Freezing Aeolian Soil in West Area of Liaoning Province[J]. Rock and Soil Mechanics, 2006, 27(3):418-422. |
| [5] | 张向东, 刘功勋, 于崇, 等. 辽西地区风积土结构特性试验研究[J].岩土力学, 2008, 29(3):691-695. ZHANG Xiang-dong, LIU Gong-xun, YU Chong, et al. Testing Study on Structural Character of Aeolian Soil in Western Area of Liaoning Province[J]. Rock and Soil Mechanics, 2008, 29(3):691-695. |
| [6] | ALDAOOD A, BOUASKE M, AL-MUKHTAR M. Impact of Freeze-thaw Cycles on Mechanical Behaviour of Lime Stabilized Gypseous Soils[J]. Cold Regions Science and Technology, 2013, 99:38-45. |
| [7] | PARK J H, LEE J S. Characteristics of Elastic Waves in Sand-silt Mixtures due to Freezing[J]. Cold Regions Science and Technology, 2013, 99:1-11. |
| [8] | CROWTHER, G. Frozen Soil Strength Criteria for Lateral Pile Analysis [J]. |
| [9] | 金龙, 汪双杰, 陈建兵. 高含冰量冻土的融化压缩变形机理[J].公路交通科技, 2012, 29(12):7-13. JIN Long, WANG Shuang-jie, CHEN Jian-bing. Mechanism of Thaw Compression Deformation of Ice-rich Frozen Soil[J]. Journal of Highway and Transportation Research and Development, 2012, 29(12):7-13. |
| [10] | 黄勇, 方靖, 张元才.高寒、高海拔地区道路安全运营管理应用技术[J].公路交通科技, 2012, 29(6):98-104. HUANG Yong, FANG Jing, ZHANG Yuan-cai. Operation and Management of Road Safety Applied Technology in Alpine High Altitude Area [J].Journal of Highway and Transportation Research and Development, 2012, 29(6):98-104. |
| [11] | 王大鹏, 傅智, 易洪, 等. 多年冻土区水泥混凝土路面下冻土路基温度场数值分析[J].公路交通科技, 2009, 26(1):45- 56. WANG Da-peng, FU Zhi, YI Hong, et al. Numerical Simulation of Thermal Field of Roadbed under Cement Concrete Pavement in Permafrost Region [J].Journal of Highway and Transportation Research and Development, 2009, 26(1):45-56. |
| [12] | 汪海年, 侯仲杰, 杨玉杰. 多年冻土路基对流换热试验方法[J].公路交通科技, 2009, 26(3):43-48. WANG Hai-nian, HOU Zhong-jie, YANG Yu-jie. Testing Method of Convective Heat Transfer for Permafrost Embankments[J].Journal of Highway and Transportation Research and Development, 2009, 26(3):43-48. |
| [13] | BRAY M T. Secondary Creep Approximations of Ice-rich Soils and Ice Using Transient Relaxation Tests[J]. |
| [14] | 董连成, 张公, 赵淑萍, 等.冻土蠕变指标试验研究[J].冰川冻土, 2014, 36(1):130-136. DONG Lian-cheng, ZHANG Gong, ZHAO Shu-ping, et al. Experimental Study of the Creep Indexes of Frozen Soil[J].Journal of Glaciology and Geocryology, 2014, 36(1):130-136. |
| [15] | 赵晓东, 周国庆. 温度梯度冻土蠕变变形规律和非均质特征[J].岩土工程学报, 2014, 36(2): 390-394. ZHAO Xiao-dong, ZHOU Guo-qing. Creep Deformation and Heterogeneous Characteristics for Frozen Soils with Thermal Gradient[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(2):390-394. |
| [16] | 尹晓文, 傅强, 马昆林.冻土三轴蠕变非线性数学模型研究[J].冰川冻土, 2013, 35(1):171-176. YIN Xiao-wen, FU Qiang, MA Kun-lin. SStudy of the Nonlinear Mathematical Model for Triaxial Creep of Frozen Soil[J].Journal of Glaciology and Geocryology, 2013, 35(1):171-176. |
| [17] | 袁文华. 人工冻土黏弹塑性本构参数反分析研究[J].岩土力学, 2013, 34(11):3091-3095. YUAN Wen-hua. Back Analysis of Viscoelasto-plastic Constitutive Parameters of Artificial Frozen Soil[J]. Rock and Soil Mechanics, 2013, 34(11):3091-3095. |
| [18] | 汪承维, 李栋伟. 深部人工冻土黏弹塑损伤耦合本构模型研究及其验证[J].冰川冻土, 2013, 35(5):1219-1223. WANG Cheng-wei, LI Dong-wei. Study and Verification of Laboratory Prepared Frozen Soil Viscoelastic-Plastic Damage Coupling Constitutive Model[J]. Journal of Glaciology and Geocryology, 2013, 35(5):1219-1223. |
| [19] | 李东庆, 周家作, 张坤, 等. 季节性冻土的水-热-力建模与数值分析[J]. 中国公路学报, 2012, 25(1):1-7. LI Dong-qing, ZHOU Jia-zuo, ZHANG Kun, et al. Modelling and Numerical Analysis of Moisture, Heat and Stress in Seasonal Frozen Soil[J]. China Journal of Highway and Transport, 2013, 35(5):1219-1223. |
| [20] | 高文华, 陈秋南, 黄自永, 等. 考虑流变参数弱化综合影响的软岩蠕变损伤本构模型及其参数智能辨识[J].土木工程学报, 2012, 45(2):104-110. GAO Wen-hua, CHEN Qiu-nan, HUANG Zi-yong, et al. Study on the Creep Damage Constitutive Model of Soft Rocks Considering Rheological Softening and Intelligent Identification of the Parameters[J]. China Civil Engineering Journal, 2012, 45(2):104-110. |
| [21] | 杨文东, 张强勇, 张建国, 等. 基于FLAC3D 的改进Burgers 蠕变损伤模型的二次开发研究[J]. 岩土力学, 2010, 31(6): 1956-1964. YANG Wen-dong, ZHANG Qiang-yong, ZHANG Jian-guo, et al. Second Development of Improved Burgers Creep Damage Constitutive Model of Rock Based on FLAC3D[J]. Rock and Soil Mechanics, 2010, 31(6): 1956-1964. |
| [22] | 刘东燕, 赵宝云, 朱可善, 等. 砂岩直接拉伸蠕变特性及Burgers模型的改进与应用[J].岩土工程学报, 2011, 33(11):1740-1744. LIU Dong-yan, ZHAO Bao-yun, ZHU Ke-shan, et al. Direct tension Creep Behaviors of Sandstone and Improvement and Application of Burgers Model[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(11):1740-1744. |
| [23] | 齐亚静, 姜清辉, 王志俭, 等. 改进西原模型的三维蠕变本构方程及其参数辨识[J]. 岩石力学与工程学报, 2012, 31(2):347-355. QI Ya-jing, JIANG Qing-hui, WANG Zhi-jian, et al. 3D Creep Constitutive Equation of Modified Nishihara Model and Its Parameters Identification[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2):347-355. |
 2015, Vol. 31
2015, Vol. 31
