公路交通科技  2015, Vol. 31 Issue (4): 150-158

扩展功能

文章信息

高晋, 牛子孺, 杨路, 杨秀建, 张昆
GAO Jin, NIU Zi-ru, YANG Lu, YANG Xiu-jian, ZHANG Kun
悬架控制臂液压衬套与整车平顺性关联分析
Correlation Analysis of Suspension Control Arm Hydraulic Bushing and Ride Comfort of Full Vehicle
公路交通科技, 2015, Vol. 31 (4): 150-158
Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (4): 150-158
10.3969/j.issn.1002-0268.2015.04.026

文章历史

收稿日期：2014-06-26
引用本文 0
高晋, 牛子孺, 杨路, 杨秀建, 张昆. 悬架控制臂液压衬套与整车平顺性关联分析[J]. 公路交通科技, 2015, Vol. 31 (4): 150-158.
GAO Jin, NIU Zi-ru, YANG Lu, YANG Xiu-jian, ZHANG Kun. Correlation Analysis of Suspension Control Arm Hydraulic Bushing and Ride Comfort of Full Vehicle[J]. Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (4): 150-158.
悬架控制臂液压衬套与整车平顺性关联分析
高晋, 牛子孺, 杨路, 杨秀建, 张昆    
昆明理工大学 交通工程学院, 云南 昆明 650500
收稿日期:2014-06-26;
基金项目：国家自然科学基金项目(51465023);昆明理工大学人才培养资助项目(KKSY201402065).
作者简介: 高晋(1982-),男,云南宣威人,博士.
通讯作者：高晋(1982-),男,云南宣威人,博士.
摘要：为准确分析比较某实车前双横臂悬架安装的液压衬套与传统橡胶衬套对车辆性能的影响,通过试验得到该控制臂液压衬套的静态和动态力学特性,在ADAMS中建立了其力学模型,并在此基础上搭建了整车仿真模型。用谐波叠加法构建了不同等级的随机路面谱。摆臂采用液压衬套和橡胶衬套时,在随机路面和凸块路面上分别对整车模型进行平顺性仿真,通过功率谱估计得到了脚部地板和座椅导轨处垂向和纵向加速度的频谱特性和均方根值,同时分别对整车模型进行了操纵稳定性仿真。最后,对比分析了液压衬套刚度改变对车辆平顺性的影响。结果表明: 该车使用液压衬套或传统橡胶衬套对操稳性的影响很小;在A、B级路面上,使用液压衬套时,车辆的平顺性会更好,而对于凸块路面,使用液压衬套时平顺性会差; 液压衬套刚度增加后,对于A、B级路面和凸块路面,垂向加速度均方根值有所增大,对于D级路面则变化很小,凸块路面垂向和纵向加速度曲线响应略为变慢,曲线的振荡时间也变长。
关键词： 汽车工程     液压衬套     频谱分析     动刚度     平顺性    
Correlation Analysis of Suspension Control Arm Hydraulic Bushing and Ride Comfort of Full Vehicle
GAO Jin , NIU Zi-ru, YANG Lu, YANG Xiu-jian, ZHANG Kun     
School of Transportation Engineering, Kunming University of Science and Technology, Kunming Yunnan 650500, China
Abstract:To precisely analyze and compare the effects of hydraulic bushing and traditional rubber bushing on the front double wishbone suspension on vehicle performance,the static and dynamic properties of the hydraulic bushing on the control arm are tested. The mechanical model is established by ADAMS, and the full vehicle model is established on this basis. The random road surface spectra of different levels are built by using the harmony superposition method. When hydraulic bushing and rubber bushing is used on the control arm respectively,the ride comfort simulation of full vehicle is carried out on random and bump roads. The frequency spectrum characteristic and RMS of vertical and longitudinal accelerations of the foot floor and the seat rail are calculated by power spectrum estimation, and the handling stability of the full vehicle is simulated respectively. At last, the effects of the change of hydraulic bushing stiffness on ride comfort are compared. The result shows that (1) the effect on the vehicle handling stability is very small,regardless of using hydraulic bushing or rubber bushing; (2) the ride comfort of the vehicle is better on level A and level B roads but the ride comfort is worse on bump road when using hydraulic bushing; (3) larger hydraulic bushing stiffness makes vertical acceleration RMS increase on level A, level B and bump roads, but the variety of RMS is very small on level D road,the responses of vertical and longitudinal acceleration curves are slower, and the time oscillation of the curves are longer on bump road.
Key words: automobile engineering     hydraulic bushing     frequency spectrum analysis     dynamic stiffness     ride comfort    
0 引言

悬架与车身控制臂连接处的衬套需具有衰减来自路面或者车轮不平衡激励的作用，因此，希望衬套元件具有大的阻尼。传统的橡胶衬套由金属元件和橡胶组成，其结构简单，但动刚度和阻尼滞后角的特性曲线基本上不随激励频率变化。目前汽车悬架中广泛应用的橡胶衬套阻尼滞后角在10°以下，这对大振幅振动的衰减效果较弱[1]。液压衬套是在传统的橡胶衬套基础上增加液体阻尼机构形成的具有非线性特性的隔振元件。液压衬套与发动机上的液阻悬置动态特性都有随激振振幅和激振频率变化而变化的特性，但也有不同。例如，液压衬套滞后角峰值频率随激振振幅的变化很大，而液阻悬置滞后角峰值频率几乎不随激振振幅变化。另外，液压衬套可在较宽的频率范围提供大阻尼(滞后角大于15°)，而液阻悬置只在某一频率附近提供大阻尼。

目前国内外学者从液压橡胶元件的试验、建模、计算分析等不同的角度进行了研究。Karlsson和Persson[2]研究了描述液压橡胶件振幅相关性和频率相关性的黏弹塑性模型，但此模型不能很好地体现液阻橡胶元件的动态特性。Svenson[3]提出了由一个非线性弹簧模型、若干个流体模型和弹塑性模型并联的一维模型，此模型在小振幅激励下的预测精度不够理想。文献[4]阐述了液压橡胶元件流固耦合模型的建模方法，将建立的VE和VEP模型用于液压衬套动态特性流固耦合计算分析。文献[5]建立了液压衬套动态特性计算分析参数模型，与试验值对比证明了模型的正确性，并给出了悬架控制臂使用液压衬套前后转向盘振动情况的对比分析实例。如今，液压衬套在汽车悬架上的使用日趋广泛，然而，在汽车设计方面，关于悬架摆臂液压衬套对车辆性能影响的研究却较少。本文基于液压衬套试验测量的数据，通过ADAMS建立悬架摆臂处的液压衬套模型，分析其对车辆操控性、平顺性的影响。 1 液压衬套的结构及静刚度测量

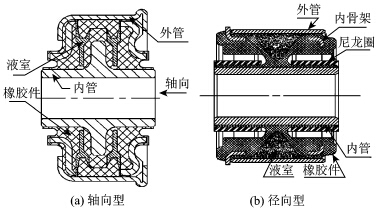
目前在汽车悬架控制臂中使用的液压衬套有两种类型：一种是轴向型，如图 1(a)，一种是径向型，如图 1(b)，它们可在低频、大振幅运动时分别在轴向和径向提供大阻尼，以衰减来自路面和车轮的不平衡激励。因液压衬套液室中的液体不可压缩，在装配衬套时，如果液室中不装液体，液压衬套就变为普通的橡胶衬套。

图 1 液压衬套结构Fig. 1 Structure of hydraulic bushing
图选项

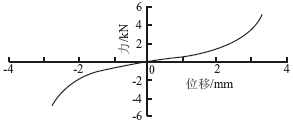
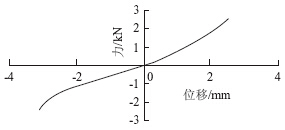
液压衬套的静态特性试验主要是测量轴向(z向)和两个径向(x向、y向)的刚度特性。测量时将衬套试验件固定在测试台上，对试验件施加载荷，得出力-位移曲线[6]。图 2、图 3分别为试验测量得到的液压衬套的1个径向刚度(y向)和轴向刚度曲线。

图 2 液压衬套径向刚度曲线Fig. 2 Radial stiffness curve of hydraulic bushing
图选项

图 3 液压衬套轴向刚度曲线Fig. 3 Axial stiffness curve of hydraulic bushing
图选项
2 液压衬套动刚度和滞后角测量 2.1 液压衬套动刚度和滞后角

试验时，将液压衬套的一端和试验台的作动端相连，另一端固定于试验台上。首先给液压衬套一定的预载荷，大小为其所受的静载荷，然后在作动头的一端施加位移激励x(t)=X0sin(ω0t)。其中，X0表示激振幅；ω0表示激励频率。记录和作动头端相连的位移传感器的位移信号x(t)和与固定端相连的力传感器信号F(t)。

由于液压衬套的非线性特性，测得的力传感器信号F(t)不仅包含与位移激励信号x(t)同阶的频率ω0，而且还包含高阶分量。F(t)可表示为：

式中，F0为静态载荷;Fm和θm分别为m阶正弦力响应的复值和滞后角，定义复刚度为：
式中，F(ω)和X(ω)分别为时域函数F(t)和x(t)的傅里叶变换。假定与激励频率ω0同阶的力响应F1远大于F0及高阶响应的复值，则：

式中，F1和θ1分别是1阶正弦力响应的复值和滞后角。

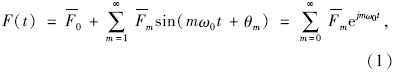
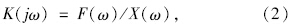
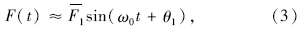
液压衬套在ω=ω0时的复刚度为：

式中K1,K2分别为存储刚度和损失刚度。

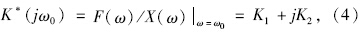
动刚度Kd和滞后角θ定义为：

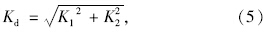
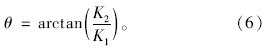
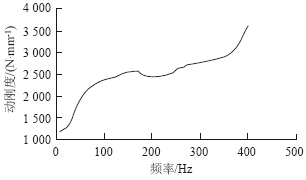
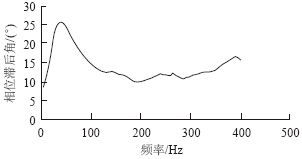
图 4、图 5分别为测量得到的液压衬套动刚度和滞后角曲线。可以看出，液压衬套的动刚度和滞后角曲线随激励振幅的变化而变化。动刚度曲线随频率的增加而明显增加；滞后角曲线有一个峰值频率，其值10～15 Hz，在高于峰值频率的频率范围内，液压衬套的滞后角随频率增加而减小。由于液压衬套主要在低频范围内提供大的阻尼滞后角，因此它比动刚度更重要。

图 4 液压衬套动刚度曲线Fig. 4 Dynamic stiffness curve of hydraulic bushing
图选项

图 5 液压衬套滞后角曲线Fig. 5 Lag angle curve of hydraulic bushing
图选项
3 整车仿真模型的建立

图 6为在ADAMS中建立的双横臂前悬架，其下摆臂后衬套为液压衬套，衬套的仿真数据根据上文的试验测量数据得到。关于液压衬套刚度变化对车辆平顺性影响的分析可参考文献[7]的方法。

图 6 液压衬套安装位置Fig. 6 Mounting position of hydraulic bushing
图选项

整车仿真分析模型的前悬架为上述带液压衬套的双横臂悬架，后悬架为空间多连杆悬架，轮胎模型为MF_TIRE。整车模型的建模参数见表 1。

表 1 整车建模参数 Tab. 1 Modeling parameters of full vehicle
参数 前悬架 后悬架
轴重/kg 947 702
弹簧刚度/ (N·mm-1) 26 40
悬架刚度(同向)/(N·mm-1) 26.6 22.84
悬架刚度(反向)/(N·mm-1) 78.59 48.29
悬架偏频/Hz 1.31 1.51
轮胎刚度/(N·mm-1) 202 202
轮胎自由半径/mm 316.7 316.7
轴距/mm 2 702
轮距/mm 1 542
质心高度/mm 560
表选项
4 液压衬套与橡胶衬套仿真分析对比 4.1 随机路面和凸块路面的建立

路面不平度一般可以通过两种方法得到：一种是试验测试，另一种是用路面不平度功率谱密度逆推路面不平度，这种方法多用于虚拟仿真环境中。生成路面不平度的功率谱分析模型有多种方法，目前最普遍的是谐波叠加法。该方法的主要思想是将路面不平度函数表示成若干具有随机相位的正弦函数之和[8, 9, 10, 11]。

路面不平度的方差σx2可由功率谱密度Gq(f)在频域内积分得到，即：

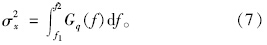
将频率上下限(f1,f2)划分成长度为Δfi的n个小区间，每个小区间的中心频率为fm－i，即fm－i=(fi+fi+1)/2，其对应的谱密度值为Gq(fm－i)，用Gq(fm－i)代替Gq(f)在整个区间的值，则路面不平度方差σx2为：

每个小区间对应的正弦波函数qi(x)为：

式中θi为服从高斯分配的随机数。将每个小区间的正弦波函数qi(x)叠加起来，就得到频域路面随机位移输入q(x)：

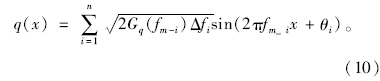
若是三维路面，则路面不平度函数q(x,y)为：

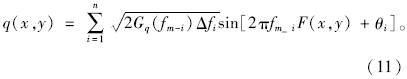
将随机路面应用到整车进行平顺性仿真时，需建立相应的路面模型文件。在ADAMS中，路面模型文件采用(.rdf)文件的形式，是基于三维网格法构建适用于ADAMS的三维路面，其核心是路面节点和路面单元。路面节点是四维数组，由节点序号和该节点的3个坐标组成；路面单元是五维数组，由3个节点序号、该单元的静摩擦系数和动摩擦系数组成[12]。

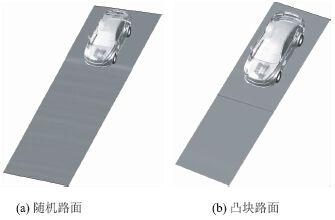
基于上述谐波叠加法，通过MATLAB编制程序仿真得到所需要的三维路面不平度特征，然后按照通用路面模型标准生成路面文件，导入ADAMS，从而得到所需要的路面文件。图 7为所建立的D级随机路面和凸块路面[13]。

图 7 随机路面和凸块路面Fig. 7 Random road and bump road
图选项
4.2 不同路面的平顺性仿真分析对比

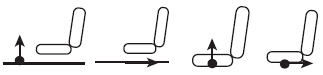
在随机路面车辆行驶时，脚步地板、座椅导轨处的垂向和纵向加速度方向如图 8所示。

图 8 脚步地板和座椅导轨位置Fig. 8 Positions of foot floor and seat rail
图选项

通过传感器测量得到脚步地板、座椅导轨处的加速度响应曲线。再计算得到这两个位置的频谱特性，即这两个位置的功率谱密度。振动响应的功率谱密度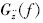与路面位移输入功率谱密度Gq(f)有密切关系，可用下式表示：

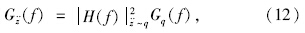
式中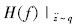为系统响应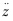对输入q的频率响应函数的模，即幅频特性，它由车辆的簧载质量、非簧载质量、悬架刚度和阻尼、轮胎刚度和阻尼共同决定。响应的均方根值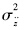为：

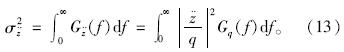
采用基于周期改进的Welch算法计算响应的功率谱密度。周期法的基本思想是对随机信号x(n)的N点观察数据xN(n)进行傅里叶变换得到X(ejω)，取其幅值的平方除以N，作为对信号x(n)的真实功率谱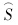(ejω)[14]：

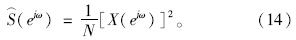
Welch算法是把xN(n)分成L段，对每段数据加窗后分别求取功率谱密度，而后取平均值。

图 9是在A级路面上以140 km/h行驶，分别采用该液压衬套和同样静刚度的纯橡胶衬套时，仿真得到的脚步地板垂向加速度频谱。

图 9 A级路面脚步地板垂向加速度频谱Fig. 9 Frequency spectra of foot floor vertical acceleration on class A road
图选项

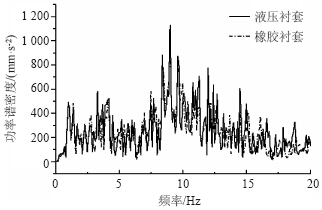
图 10是在B级路面上以100 km/h行驶，分别采用该液压衬套和相同静刚度纯橡胶衬套时，仿真得到的脚步地板垂向加速度频谱。

图 10 B级路面脚步地板垂向加速度频谱Fig. 10 Frequency spectra of foot floor vertical acceleration on class B road
图选项

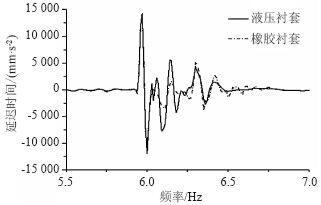
图 11是在凸块路面上以30 km/h行驶，分别采用相同静刚度的纯橡胶衬套和液压衬套时，仿真得到的座椅导轨垂向加速度响应曲线。可以看出，垂向加速度响应曲线有两个峰值，分别对应车辆前后车轮通过凸块的情况。当使用液压衬套时，响应曲线在两个峰值之间有更大的波动。

图 11 凸块路面座椅导轨垂向加速度响应曲线Fig. 11 Vertical acceleration response curves of seat rail on bump road
图选项

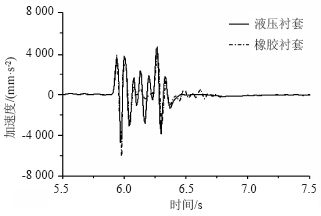
图 12是在凸块路面上以30 km/h行驶，分别采用相同静刚度的纯橡胶衬套和液压衬套时，仿真得到的座椅导轨纵向加速度响应曲线。可以看出，当使用液压衬套时，纵向响应曲线在两个峰值之间有更大的波动。

图 12 凸块路面座椅导轨纵向响应曲线Fig. 12 Longitudinal acceleration response curves of seat rail on bump road
图选项

表 2是液压衬套和橡胶衬套的平顺性分析结果。可以看出，在A,B级路面上，当摆臂使用液压衬套时，仿真计算得到的脚步地板垂向加速度均方根值比使用橡胶衬套时计算得到的脚步地板垂向加速度均方根值要小。而对于凸块路面，使用液压衬套时计算得到的座椅导轨的垂向和纵向加速度均方根值更大。

表 2 液压和橡胶衬套平顺性分析结果 Tab. 2 Analysis result of ride comfort after using hydraulic and rubber bushings
信号 路面
信息		 加速度均方根值/
(mm·s-2)		 数据处理
方式
液压衬套 橡胶衬套
脚部地板垂向 A级 312.97 314.43 滤波数据
B级 465.14 473.39
座椅导轨垂向 凸块 807.81 713.84 原始信号
座椅导轨纵向 凸块 499.37 449.81
表选项
4.3 瞬态操纵稳定性仿真分析对比

瞬态操纵稳定性分析时按正弦扫频方式打方向盘。仿真时，初始频率为0.2 Hz，最大频率为3.8 Hz，转向频率增加速率为0.2 Hz/s，方向盘最大转角为25°[15]。

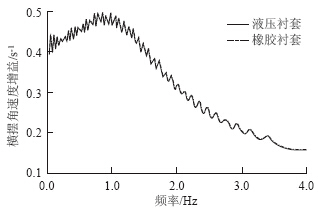
图 13是仿真得到的横摆角速度对方向盘转角增益随频率的变化曲线，即幅频特性曲线。随着频率的增加，幅值比也增加，到某一频率时，幅值比达到最大，车辆处于共振状态。当频率再增加时，幅值比减小。可以看出，摆臂采用液压衬套和橡胶衬套时，两条曲线基本重合，说明采用液压衬套对横摆角速度响应的影响不大。

图 13 横摆角速度幅频特性曲线Fig. 13 Amplitude-frequency characteristic curves of yaw rate
图选项

图 14是仿真得到的横摆角速度-方向盘转角延迟时间随频率的变化曲线，延迟时间反应了车辆相应的快慢。延迟时间随频率增加而增加，到某一频率时，延迟时间最大，此时车辆的响应最慢。此后频率增加，延迟时间减小。可以看出，摆臂采用液压衬套和橡胶衬套时，两条曲线基本重合，说明采用液压衬套对车辆响应快慢的影响不大。

图 14 横摆角速度-方向盘转角延迟时间曲线Fig. 14 Delay time curves of yaw rate vs. steering wheel angle
图选项
5 液压衬套刚度变化对平顺性影响的仿真分析

图 15为试验测量得到的液压衬套径向刚度曲线(图例中baseline为液压衬套的基准刚度，case01为改变后的液压衬套刚度，下同)。该液压衬套的动刚度和滞后角曲线与上文的分析结果一样。下面分析液压衬套刚度改变对脚步地板和座椅导轨加速度响应的影响。

图 15 液压衬套刚度曲线Fig. 15 Stiffness curves of hydraulic bushing
图选项

图 16、图 17分别为仿真车辆在A级路面上以140 km/h 行驶时，经过滤波计算得到的脚部地板和座椅导轨垂向加速度频谱。图中两条曲线分别对应改变前的衬套基准刚度和改变后的衬套刚度。可以看出，刚度增加后，脚部地板和座椅导轨功率谱密度曲线的尖峰变得更多。另一方面，脚部地板比座椅导轨的功率谱曲线数值更大，表明脚部地板的振动强度比座椅导轨处更大。

图 16 A级路面脚部地板垂向加速度频谱Fig. 16 Frequency spectra of foot floor vertical acceleration on level A road
图选项

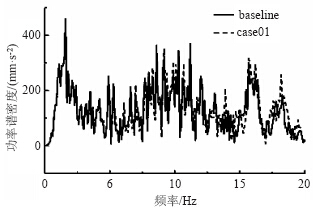
图 17 A级路面座椅导轨垂向加速度向频谱Fig. 17 Frequency spectra of seat rail vertical acceleration on level A road
图选项

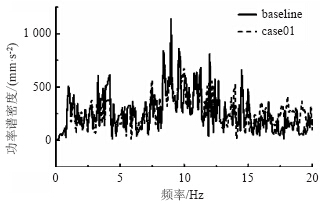
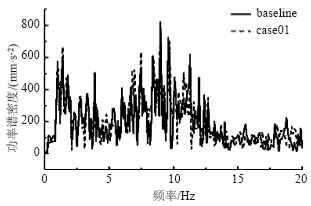
图 18、图 19分别为仿真车辆在B级路面上以100 km/h行驶时，经过滤波计算得到的脚部地板和座椅导轨垂向频谱。可以看出，相对于A级路面，B级路面计算得到的脚部地板和座椅导轨处的功率谱密度曲线数值都大。同样，对于B级路面，刚度增加后，脚部地板和座椅导轨功率谱密度曲线的尖峰变得更多，表明该处的振动变得更大。

图 18 B级路面脚部地板垂向加速度频谱Fig. 18 Frequency spectra of foot floor vertical acceleration on level B road
图选项

图 19 B级路面座椅导轨垂向加速度频谱Fig. 19 Frequency spectra of seat rail vertical acceleration on level B road
图选项

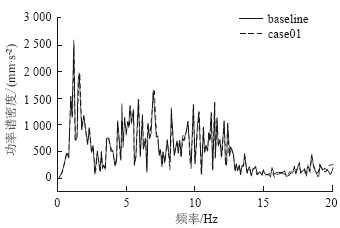
图 20、图 21分别为仿真车辆在D级路面上以60 km/h 行驶时，经过滤波计算得到的脚部地板和座椅导轨垂向频谱。可以看出，相对于A级路面和B级路面计算结果，尽管仿真车速降到60 km/h，D级路面计算得到的脚部地板和座椅导轨处的功率谱密度曲线数值明显变大很多。

图 20 D级路脚部地板垂向加速度频谱Fig. 20 Frequency spectra of foot floor vertical acceleration on level D road
图选项

图 21 D级路面座椅导轨垂向加速度频谱Fig. 21 Frequency spectra of seat rail vertical acceleration on level D road
图选项

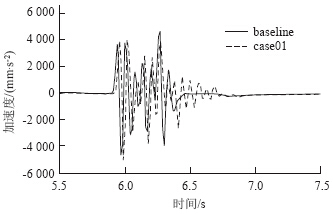
图 22 、图 23分别为仿真车辆以30 km/h通过凸块路面时，计算得到的脚部地板垂向加速度和纵向加速度时程曲线。可以看出，刚度增加后，脚步地板的纵向和垂向加速度响应都略为变慢，同时振荡时间也变长。

图 22 凸块路面脚步地板垂向加速度曲线Fig. 22 Foot floor vertical acceleration curves on bump road
图选项

图 23 凸块路面脚步地板纵向加速度曲线Fig. 23 Foot floor longitudinal acceleration curves on bump road
图选项

表 3为对随机路面和凸块路面仿真计算得到的加速度均方根值。其中随机路面的均方根值是原始信号滤波计算得到的结果，凸块路面是原始信号计算得到的结果。刚度增加后，对于A,B级路面，垂向加速度均方根值有所增大；对于D级路面，垂向加速度均方根值变化很小；对于凸块路面，垂向加速度均方根值有所增加，纵向均方根值有所减小。

表 3 液压衬套不同刚度的平顺性分析结果 Tab. 3 Ride comfort analysis results of the different stiffness hydraulic
信号 路面信息 加速度均方根值/
(mm·s-2)		 变化率/
%		 数据处理
方式
baseline case01
脚部地板
垂向		 A级 327.23 347.64 6.24 滤波数据
B级 472.73 483.34 2.24
D级 1373.80 1375.40 0.16
凸块 1006.06 1056.48 5.01
脚部地板
纵向		凸块 497.61 493.77 -0.77 原始数据
座椅导轨
垂向		 A级 223.66 233.90 4.58滤波数据
B级 368.37 370.44 0.50
D级 975.86 976.93 0.11
凸块 807.86 849.53 5.16
座椅导轨
纵向		 凸块 499.37 494.84 -0.91 原始信号
表选项

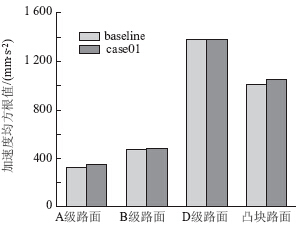
图 24为液压衬套刚度改变前后车辆在各种路面上行驶时，仿真得到的脚部地板垂向加速度均方根值比较。

图 24 脚部地板垂向加速度均方根值比较Fig. 24 Comparison of foot floor vertical acceleration RMSs
图选项
6 结论

(1)针对某车前悬架控制臂液压衬套，根据实测的该衬套静态和动态试验曲线，在ADAMS中建立其力学模型。基于谐波叠加法，建立不同等级的随机路面和凸块路面。通过功率谱估计计算得到脚部地板和座椅导轨处的频谱特性。

(2)对比分析了该衬套采用液压衬套和同样静刚度的橡胶衬套时对平顺性和操纵稳定性的影响。结果表明,对操纵稳定性的影响很小；当摆臂使用液压衬套时，在A,B级路面上仿真计算得到的两个位置垂向加速度均方根值要小；而对于凸块路面，使用液压衬套时计算得到的座椅导轨的垂向和纵向加速度均方根值更大，且在前后轮通过凸块的时间段内，曲线有更大的波动。

(3)研究了液压衬套刚度变化对该车平顺性的影响。结果表明，刚度增加后，脚部地板和座椅导轨位置：对于A,B级路面，垂向加速度均方根值有所增大；对于D级路面，垂向加速度均方根值变化很小；对于凸块路面，垂向加速度均方根值有所增加，纵向均方根值有所减小。

参考文献
[1] 马天飞,刘亚洲,乔雪冰,等.悬架液压衬套的液固耦合建模及动态特性分析[J].中国机械工程,2013,24(7):857-860. MA Tian-fei, LIU Ya-zhou, QIAO Xue-bing, et al. Fluid-Structure-interaction Modeling and Dynamic Behavior Analysis for Hydrobushing of Suspension[J].China Mechanical Engineering, 2013,24(7):857-860.
[2] KARLSSON F, PERSSON A. Modeling Non-linear Dynamics of Rubber Bushings: Parameters Identification and Validation[D]. Lund, Sweden: Lund University, 2003.
[3] SVENSSON M, HAKANSSON M. Hydrobushing Model for Mutibody Simulation[D]. Lund, Sweden: Lund University, 2004.
[4] 潘孝勇,谢新星,上官文斌.变振幅激励下液阻橡胶隔振器动态特性分析[J].振动与冲击,2012,31(1):144-149. PAN Xiao-yong, XIE Xin-xing, SHANGGUANG Wen-bin. Dynamic Properties Analysis for a Hydraulic Rubber Isolator under Excitations with Different Amplitudes[J].Journal of Vibration and Shock, 2012,31(1):144-149.
[5] 上官文斌,徐驰.汽车悬架控制臂液压衬套动态特性实测与计算分析[J].振动与冲击,2007,26(9):7-10. SHANGGUANG Wen-bin, XU Chi. Experiment and Calculation Methods for Analyzing Dynamic Performances of Hydraulic Bushings Used in Control Arms of a Suspension [J]. Journal of Vibration and Shock, 2007,26(9):7-10.
[6] 吕振华,上官文斌,梁伟,等.液阻悬置动态特性试验方法及实测分析[J].中国机械工程,2004,15(2):182-186. LÜ Zhen-hua, SHANGGUAN Wen-bin,LIANG Wei, et al. Experimental Methods and Test Evaluation for the Dynamic Characteristics of Hydraulically Damped Rubber Mount[J].China Mechanical Engineering, 2004,15(2):182-186.
[7] 李仲兴,喻广强,江洪,等.基于ADAMS的空气悬架客车平顺性仿真与试验[J].公路交通科技,2010,27(2):125-128. LI Zhong-xing,YU Guang-qiang,JIANG Hong, et al. Simulation and Test of Ride Comfort of Bus with Air Suspension Based on ADAMS[J]. Journal of Highway and Transportation Research and Development,2010,27(2):125-128.
[8] 李炜明,朱宏平,黄民永,等.路面随机谱激励的数值计算方法及统计特征[J].中国公路学报,2009,22(3):20-25. LI Wei-ming, ZHU Hong-ping, HUANG Min-yong, et al. Numerical Calculation Methods and Statistic Characters on Road Surface Random Spectral Excitation[J].China Journal of Highway and Transport,2009,22(3):20-25.
[9] 张义,莫旭辉,钟志华,等.随机路面下菱形客车平顺性研究与优化[J].中国机械工程,2011,22(23):2894-2895. ZHANG Yi, MO Xu-hui, ZHONG Zhi-hua, et al. Research and Optimization of Ride Comfort for Rhombic Bus under Random Road[J]. China Mechanical Engineering, 2011,22(23):2894-2895.
[10] LI L, SANDU C. Modeling and Simulation of 2D ARMA Terrain Models for Vehicle Dynamics Applications[DB/OL]. (2007-04-16)[2014-06-06].http://papers.sae.org/2007-01-0138.
[11] KANG D, HEO S, KIM H. Virtual Road Profile Modeling Using Equivalent Damage Method For VPG Simulation[DB/OL]. (2009-04-20)[2014-06-06]. http://papers.sae.org/2009-01-0814.
[12] 杨益明,文爱民,刘奕贯.三维路面模型的构建及其在Adams中的验证[J].公路交通科技,2010,27(12):141-144. YAND Yi-ming,WEN Ai-min,LIU Yi-guan. Reconstruction of 3D Road Model and Its Verification Based on Adams[J]. Journal of Highway and Transportation Research and Development,2010,27(12):141-144.
[13] 周长锋,李延骁,刘佳,等.基于ADAMS的脉冲路面车辆行驶平顺性仿真研究[J].拖拉机与农用运输车,2012,39(2):22-25. ZHOU Chang-feng, LI Yan-xiao, LIU Jia, et al. Ride Comfort Simulation of Vehicle on Impulse Road Based on ADAMS[J]. Tractor & Farm Transporter, 2012,39(2):22-25.
[14] 薛劲橹,王红岩,迟宝山.虚拟实验三维随机路面的建模[J].中国机械工程学报,2012,10(2):238-239. XUE Jin-lu, WANG Hong-yan, CHI Bao-shan. Stochastic 3D-road-surface Modeling for Virtual Testing[J].Chinese Journal of Construction Machinery, 2012,10(2):238-239.
[15] 高晋,杨秀建.衬套刚度对悬架C特性及瞬态操稳的灵敏度研究[J].汽车技术,2013(11):36-37. GAO Jin, YANG Xiu-jian. Sensitivity Study of Bushing Stiffness Affecting Suspension Compliance Characteristic and Transient Handing Stability[J]. Automotive Technology, 2013(11):36-37.