扩展功能
文章信息
- 魏明, 陈学武, 孙博
- WEI Ming, CHEN Xue-wu, SUN Bo
- 多模式区域公交协调调度模型和算法
- A Model and an Algorithm of Schedule Coordination for Multi-mode Regional Bus Transit
- 公路交通科技, 2015, Vol. 31 (4): 136-142
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (4): 136-142
- 10.3969/j.issn.1002-0268.2015.04.024
-
文章历史
- 收稿日期:2014-09-09
2. 南通大学 交通学院, 江苏 南通 226019
2. School of Transportation, Nantong University, Nantong Jiangsu 226019, China
近年来,国内外众多大中城市正加快构建以轨道交通为骨架、常规公交为主体的多模式公共交通网络,出行者经常需要从出发地选择一种模式或组合多交通模式到达目的地。若各模式内或模式间的相关线路班次车未能与乘客同时到达站点,或相应换乘线路班次车不能同时到达换乘点,则必然产生乘客在相关站点的等待时间。各交通模式运营网络之间缺少协调管理和集成服务信息,换乘不便严重制约了公共交通网络的运输效率,如何协同编制某区域内各交通模式的时刻表来最大限度地满足乘客出行需求是交通领域研究的热点问题之一。目前,国内外学者较多关注某区域内单交通模式时刻表的协同编制问题,其中文献[1]研究了列车同步换乘问题;文献[2, 3, 4]探讨了地铁时刻表同步换乘问题;文献[5, 6, 7, 8, 9]描述了几类区域公交时刻表同步换乘问题。而多交通模式时刻表同步换乘问题鲜有涉及,仅陈旭梅等[10]探讨了一类公交与轨道交通运营调度协调模型;宗芳等[11]建立了综合客运枢纽内各交通模式协调的调度模型。上述研究未考虑各交通模式的特征,而将它们均看作一个决策变量,这与实际不相符。
根据各模式的运营特点,将多模式交通网络划分为两大类,不断调整行车时刻表以适应区域内客流波动规律。如常规公交,记为第1层次公交网络;营运计划一旦制订好就少有变动,如地铁、长途客运等,记为第2层次公交网络。 本文以第1层次公交网络的常规公交为研究对象,考虑公交内部及公交和第2层次公交网络的地铁、长途客运之间的换乘衔接问题,在满足发车时刻在相应时间范围内、发车间隔满足最小和最大发车间隔等贴近实际约束条件基础上,以全网络乘客非换乘和换乘等车时间最小及所有车辆到达站点无泊位次数最少为目标,建立多模式区域公共交通行车时刻表(Multi-mode Regional Bus Transit Schedule,MMRBTS) 的同步换乘数学模型,并用改进细菌觅食优化算法求解该问题的满意解。 1 问题描述及数学模型 1.1 假设
(1)对任意线路,车辆在站点间的行程时间不受随机事件的影响。
(2)通过智能公交数据采集平台,可获取乘客在各站点乘坐各线路的客流到达规律以及乘客在各线路之间的换乘比例。
(3)多模式不同线路之间的换乘站点可以实现无缝衔接,乘客在换乘过程中的步行时间忽略不计。
(4)车辆的载客能力足够大,不存在站点乘客滞留情况。 1.2 参数
|·|表示某集合的元素数量。
G=(L,S)为多模式交通网络,包括第1层次和第2层次网络G1=(L1,S1)和G2=(L2,S2),满足L=L1∪L2和S=S1∪S2,其中L1∪L2=(L1,L2,…,L|L|)为线路集合,S1∪S2=(s1,s2,…,s|S|)为站点集合。
Li=(si1,si2,…,si|Li|)∈L1∪L2(i=1,2,…,|L1|,|L1|+1,…,|L1|+|L2|),其中sik∈S1∪S2(k=1,2,…,|Li|)为其途经的第k个站点。显然,当|L2|=0时,该问题转化为仅考虑常规公交的单模式区域公交行车时刻表(Single-mode Regional Bus Transit Schedule,SMRBTS)生成问题。
在某个时间段[Ar-1,Ar]内,线路Li(i=1,2,…,|L|)的发车次数、最大和最小发车间隔分别表示为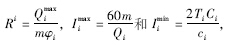 ,式中,Ar-1和Ar分别为该时段的起始和结束时间,Qi和Qmaxi<分别为相关线路在相应时段内的流量和最大断面流量;Ci,ci,φi分别为相关线路运营成本、投入费用和满载率;Ti为运行周期;m为车辆额定载客量。同理,Rj为线路Lj的发车次数。
,式中,Ar-1和Ar分别为该时段的起始和结束时间,Qi和Qmaxi<分别为相关线路在相应时段内的流量和最大断面流量;Ci,ci,φi分别为相关线路运营成本、投入费用和满载率;Ti为运行周期;m为车辆额定载客量。同理,Rj为线路Lj的发车次数。
tisiku=tisik-1u+stoptime+span(sik-1,sik)为线路Li从始发站点si1开出的第u班次车到达站点sik(∀sik∈Li)的时间,式中,span(sik-1,sik)为车辆在站点sik-1和sik之间的行程时间;stoptime为车辆在站点的上下客时间。
Pik(t)=∫0tfik(u)du为线路Li上某站点k的客流到达规律,式中fik(t)为相应的客流到达密度函数。显然,Pi(t)= Pisik(t)表示线路Li的总客流累计函数。
Pisik(t)表示线路Li的总客流累计函数。
βijz为在站点z的乘客从线路i换乘至线路j的比例。
ordLiz为站点z在线路Li中的位置。
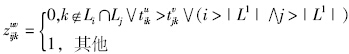
为线路i的第u班次车和线路j的第v班次车是否在站点k换乘的依据,式中tuik(tvjk)为线路Li(Lj)第u(v)班次车到达站点k的时间。
capacityk为站点k的最大停车数。
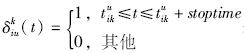 表示线路i的第u班次车在时刻t是否在站点k上下客。
表示线路i的第u班次车在时刻t是否在站点k上下客。
1.3 决策变量
tisi1u(i=1,2,…,|L|,u=1,2,…,Ri)表示第i条公交线路Li第u班次车从始发站点si1的开出时间。
1.4 目标函数
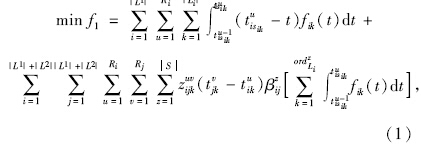
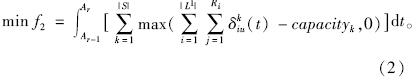
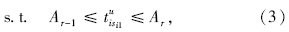
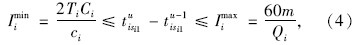
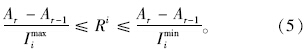
在上述模型中,式(1)和式(2)是问题的目标函数,前者表示极小化某时段内非换乘和换乘出行者在所有站点的候车时间,后者表示某时段内相关线路班次车辆到达站点的无泊位数最少(因站点缺少泊位,若各模式内的相关线路多辆车同时到达某站点,车辆占据车道造成站点附近的道路阻塞);式(3)~式(5)是问题的约束条件,其中,式(3)表示某线路在相应时段内的发车时间;式(4)表示某线路的发车间隔在一定范围内;式(5)确保某线路的发车次数满足客流需求。
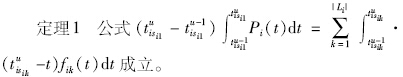
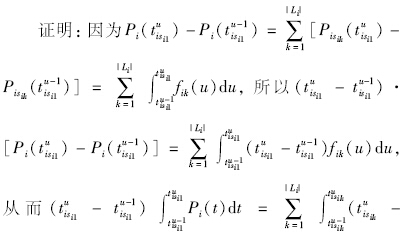
根据定理1,式(1)可以转化为式(6),其优点为计算目标函数的运算量较少,所需数据采集相对较容易获取。
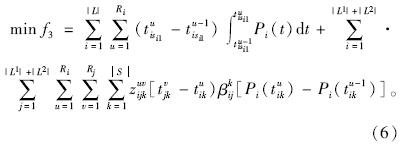
细菌觅食优化算法(Bacterial Foraging Optimiza-tion,BFO)是一种模拟大肠杆菌觅食行为的仿生搜索算法,遵循自然界优胜劣汰、适者生存的原则进行繁殖。细菌通过翻转和游动逐步趋于集中到营养丰富之处,从而找到问题的最优解。BFO是搜索速度较慢的局部优化算法,文献[12]的研究表明这取决于两点:(1)它的趋化操作缺失细菌和细菌、细菌和环境之间的信息反馈机制;(2)在繁殖和迁移操作中没有利用群体知识导致可能扼杀精英细菌,不能保持群体多样性。
针对BFO的某些弊病,本文提出求解一类MMRBTS的改进BFO。根据问题特征设计解的编码方案、产生初始种群的启发式算法、细菌觅食操作,详细过程如下。
2.1 细菌个体的编码方案
采用实数编码,细菌k的位置向量Xk=(x01,…,xR1-11,…,x0i,…,xji,…,x0|L|,…,xR|L||L|-1)表示问题的1个解,其中元素x0i和xji(∀i,j≠0)分别表示公交线路i(1≤i≤|L|)的首班车发车时刻和第j班车(1≤j≤Ri)的发车间隔,满足约束条件Ar-1≤x0i≤Ar和Iimin≤xji≤Iimax,可知tisi1u=x0i+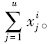
2.2 细菌个体的评价函数
目标函数f2主要减少车辆因站点缺少泊位在进站前的排队等待。令f2→0,采用约束法以f1为主目标,构造问题的单目标规划问题如下[13]:

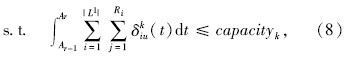
其他约束与式(2)~式(5)相同,式(8)表示某时段内该站点的车辆数可满足它的泊位限制。
本文以Fit(f)=f1为细菌个体的评价函数估计个体的优劣,求解问题的非劣解。 2.3 生成初始细菌群体
MMRBTS的众多影响因素极其复杂,随机产生的细菌个体很难是该问题的1个可行解。设计启发式算法生成可行细菌个体,组成求解该问题的初始种群。具体步骤如下。
步骤1:读取线路Li的运营参数Ar,Ar-1,Ti,Ci和ci,计算Iimin,Iimax和Ri等,令i=1。
步骤2:随机产生线路Li的首班发车时刻x0i=Ar-1+rand(Ar-Ar-1),依次计算第j班车(1≤j≤Ri)的发车间隔xji=Iimin+rand(Iimax-Iimin),若Ar-1≤tisi1u=x0i+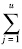 xji≤Ar-1,检验车辆途经各站点的到达时间tisi1u=x0i+
xji≤Ar-1,检验车辆途经各站点的到达时间tisi1u=x0i+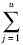 xji是否满足式(8),当xji不可行时重新计算。rand为随机数。
xji是否满足式(8),当xji不可行时重新计算。rand为随机数。
步骤3:设置i=i+1,若i≤|L|,转至步骤2;否则,算法终止,输出结果。 2.4 细菌觅食行为
在BFO中,细菌寻优由趋化、繁殖和迁徙3个操作组成,即当1个生命周期的趋化完成后,执行繁殖,然后迁移。针对上述BFO的缺陷,算法改进之处如下。
在趋化操作中,将梯度概念引入移动步长,第i个细菌朝着高适应度细菌k做翻转、前进和停止动作,使之移动到一个新位置以完成觅食过程,逐步聚集于富营养区域。第i个细菌的翻转和游动根据下式更新位置:
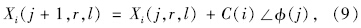
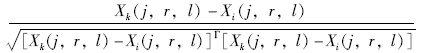 为趋化步长;∠φ(j)为第j步前进时的随机方向角。
为趋化步长;∠φ(j)为第j步前进时的随机方向角。在繁殖操作中,计算所有细菌的适应度,采用赌轮选择策略复制适应度较高的细菌,并保留了最好的细菌。
在迁徙操作中,利用群体多样性控制迁徙概率的大小,对位置相同的细菌采用随机初始化方法迁徙。由上可知,群体多样的大小与迁移概率成反比关系。
由文献[12]可知,本文设计的改进策略可加快算法收敛时间,保持群体多样性,进一步加强算法的全局搜索能力。 2.5 算法步骤
针对BFO的基本原理,BFO求解优化问题的一般过程为:先设置算法参数,产生细菌的初始群体,在此基础上细菌群体在每次迭代中进行趋化、繁殖和迁移操作,产生新一代细菌群体,逐步逼近最优解。本文提出的改进BFO的实现过程如图 1所示。
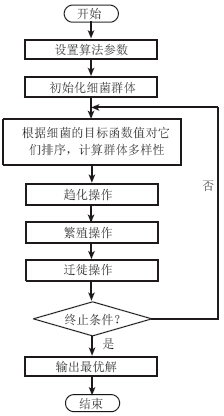
|
| 图 1 BFO的算法流程图Fig. 1 Flowchart of BFO algorithm |
本文以某区域的多模式公交网络为例,如图 2所示,它由3个公交站场(A、B和C)、5条公交线路、1条长途客运线路、1条地铁线路和2个换乘站点(I和II)组成。根据智能公交IC客流时空分布采集数据,每条公交线路的运营信息如表 1所示,地铁和长途客运线路在时段内7:00—12:00的发车间隔分别为10 min和30 min,它们的客流达到规律函数为P6(t)=0.007 1t2-4.442 3t-2 675.4和P7(t)=-0.000 8t2+1.953 5t-613.731 5,其他运营参数为capacityk=1,β16Ι=0.25,β61Ι=0.20,β17Ι=0.15,β71Ι=0.20,β14Π=0.35,β51Π=0.2。考虑公交内部及公交和地铁、长途客运之间的换乘衔接问题,协调编制5条公交线路在时间段7:00—12:00的时刻表,以追求整个多模式公交网络的运营效率最大。表 1为这些公交线路的信息。
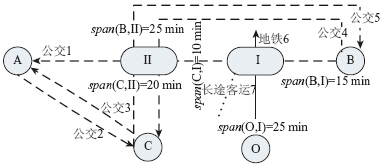
|
| 图 2 多模式公交网络Fig. 2 Multi-mode transit network |
| 线路 | 时段 | 发车间隔/min | 客流达到规律函数 |
| 1 | 7:00-11:40 | [8, 15] | P1(t)=-0.002 3t2+6.351 8t-2 127.5 |
| 2 | 6:40-12:00 | [10, 15] | P2(t)=0.000 2t2+0.388 6t-177.153 1 |
| 3 | 7:00-12:00 | [10, 20] | P3(t)=0.000 7t2+0.122 3t-952.602 7 |
| 4 | 7:00-12:00 | [10, 15] | P4(t)=-0.005 9t2+8.169 0t-2 280.1 |
| 5 | 7:00-12:00 | [15, 20] | P5(t)=-0.003 6t2+7.028 6t-2 214.7 |
利用matlab编写求解MMRBTS的改进BFO程序。算法参数设置为迭代次数200、种群规模50、趋向次数10、复制代数4、迁徙次数2,迁徙概率0.25,在CPU为Intel Pentium 2.83 GHz、内存为1.00 GB的计算机上运行实例10次,计算SMRBTS和MMRBTS两种情形下的最佳方案,结果如表 2和表 3所示。与SMRBTS相比,MMRBTS的直达乘客等待时间相差不大,虽然MMRBTS的公交线路之间的乘客总换乘时间仅增加6.94%,但其地铁、长途客运与公交之间出行者的总换乘时间减少62.85%,全网络乘客总等待时间减少3.01%,从而验证了MMRBTS的正确性和有效性。
| 方案 | 公交直达乘客 等车时间/min |
换乘等待时间/min | 总等待时 间/ min |
|
| 公交 | 非公交 | |||
| SMRBTS | 24 671 | 724 | 2 319 | 27 714 |
| MMRBTS | 24 702 | 778 | 1 424 | 26 904 |
| 偏差/% | -0.13 | -6.94 | 62.85 | 3.01 |
| 线路 | 发车时刻 | |
| SMRBTS | MMRBTS | |
| 1 | 7:00 7:09 7:21 7:31 7:44 7:54 8:04 8:16 8:25 8:34 8:43 9:04 9:15 9:24 9:38 9:50 10:05 10:15 10:24 10:36 10:47 10:56 11:07 11:21 | 7:00 7:11 7:25 7:36 7:46 7:56 8:06 8:16 8:26 8:36 8:44 8:56 9:07 9:15 9:25 9:35 9:55 10:04 10:14 10:23 10:33 10:43 10:53 11:07 11:25 |
| 2 | 6:40 6:54 7:04 7:14 7:25 7:37 7:47 7:59 8:09 8:24 8:39 8:49 9:00 9:12 9:24 9:35 9:46 9:58 10:08 10:20 10:32 10:42 10:54 11:05 11:16 11:30 11:45 | 6:40 6:50 7:01 7:12 7:25 7:39 7:49 8:02 8:17 8:30 8:43 8:56 9:07 9:21 9:31 9:45 9:59 10:10 10:24 10:35 10:48 11:02 11:12 11:27 11:37 11:50 |
| 3 | 7:00 7:13 7:30 7:48 8:03 8:15 8:27 8:39 8:57 9:11 9:24 9:36 9:50 10:02 10:15 10:29 10:40 10:51 11:12 11:23 11:33 11:44 11:55 | 7:00 7:16 7:29 7:44 8:03 8:18 8:30 8:48 9:02 9:12 9:28 9:43 9:53 10:06 10:20 10:35 10:50 11:01 11:14 11:25 11:44 11:55 12:10 |
| 4 | 7:00 7:14 7:26 7:38 7:52 8:05 8:19 8:30 8:42 8:53 9:08 9:21 9:32 9:43 9:56 10:09 10:24 10:37 10:51 11:03 11:16 11:30 11:43 11:54 | 7:00 7:13 7:24 7:38 7:50 8:03 8:18 8:28 8:39 8:54 9:07 9:18 9:32 9:45 9:59 10:11 10:24 10:36 10:47 10:59 11:12 11:25 11:36 11:48 |
| 5 | 7:00 7:16 7:35 7:52 8:07 8:25 8:40 8:55 9:11 9:29 9:47 10:05 10:23 10:38 10:58 11:14 11:31 11:48 12:05 | 7:00 7:18 7:34 7:50 8:10 8:27 8:46 9:01 9:19 9:36 9:52 10:09 10:25 10:41 10:58 11:14 11:31 11:49 12:05 |
考察capacityk对MMRBTS的影响。如图 3所示,随着capacityk的变大,虽然直达乘客的等车时间变大,但避免了因站点泊位数不足而不能实现公交车之间同步到站换乘的现象,因而全网络的乘客总等待时间逐渐减少,计算结果符合直观想象。
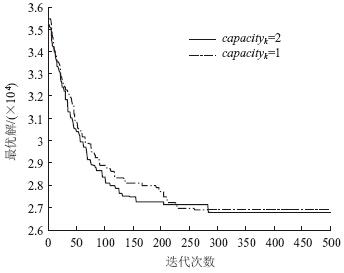
|
| 图 3 capacityk对MMRBTS的影响Fig. 3 Influence of capacityk on MMRBTS |
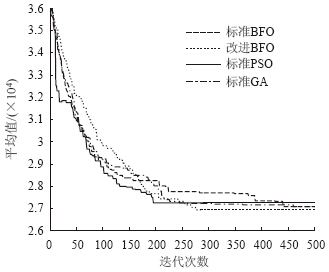
此外,比较改进BFO、BFO、PSO和GA之间性能差异,分别对测试实例运算10次,取它们各自的平均值以避免偶然现象,分析它们的仿真结果以验证算法的有效性,如图 4所示,从中可知:
|
| 图 4 不同算法的结果比较Fig. 4 Comparison analysis of results of different algorithms |
(1) BFO、PSO和GA平均迭代441、195、461次收敛局部最优,它们的最优解概率是50%、30%和40%。与GA相比,PSO和BFO快速地收敛于局部最优,但BFO和GA更容易跳出极值,从而有机会找到更好的解。因此,利用BFO求解MMRBTS是高效可行的。
(2)与标准BFO相比,改进BFO找到最优解的迭代次数减少165次,最优解概率提高35%,它们之间平均值相差0.59%,这说明将梯度概念引入移动步长,在收敛性能上有所提高,具有很好的鲁棒性,从而改进之处是有效的。 4 结论
本文以常规公交为研究对象,考虑公交内部、公交和地铁、长途客运之间的换乘衔接问题,研究了一类多目标MMRBTS,根据问题特征设计求解该问题的改进BFO,对细菌觅食过程的趋化、繁殖和迁徙操作进行了修正,结合实际数据计算某区域内几条线路的公交发车时刻表,并与BFO,PSO和GA等智能算法进行了对比分析,从而验证了模型和算法的有效性和合理性。
但是该研究仅探讨了全程车单一调度模式情形下的MMRBTS,考虑车辆容量限制约束因素,在现实中客流时空不均衡性决定了全程车、区间车和大站快车3种形式的混合发车策略更符合实际,基于此的MMRBTS将是本研究今后进一步研究的方向。
| [1] | DADUNA J R,VOSS S. Practical Experiences in Schedule Synchronization[J]. |
| [2] | KWAN C M, CHANG C S. Timetable Synchronization of Mass Rapid Transit System Using Multiobjective Evolutionary Approach[J]. |
| [3] | CHANG C S, XU D Y, QUEK H B. Pareto-optimal Set Based Multi-objective Tuning of Fuzzy Automatic Train Operation for Mass Transit System[J]. |
| [4] | KWAN C M, CHANG C S. Application of Evolutionary Algorithm on a Transportation Scheduling Problem: The Mass Rapid Transit[C]//The 2005 IEEE Congress on Evolutionary Computation. Edinburgh: IEEE, 2005:987-994. |
| [5] | CEDER A. Creating Bus Timetables with Maximal Synchronization[J]. Transportation Research, 2001,35(10):456-471. |
| [6] | 邹迎. 公交区域调度行车计划编制方法研究[J]. 交通运输系统工程与信息, 2007, 7(3): 123-126. ZOU Ying. Study on Bus Regional Scheduling Travel Plan Organizing Method[J].Journal of Transportation Systems Engineering and Information Technology,2007,7(3): 123-126. |
| [7] | 刘志钢,申金升,王海星,等.基于协同发车的区域公交时刻表生成模型研究[J].交通运输系统工程与信息,2007,7(2):345-361. LIU Zhi-gang, SHEN Jin-sheng, WANG Hai-xing, et al. Regional Public Transportation Timetabling Model with Synchronization[J]. Journal of Transportation Systems Engineering and Information Technology, 2007,7(2):345-361. |
| [8] | 石琴,覃运梅,黄志鹏.公交区域调度的最大同步换乘模型[J].中国公路学报, 2007,20(6): 453 -558. SHI Qin, QIN Yun-mei, HUANG Zhi-peng. Maximal Synchronous Transfer Model of Bus Regional Dispatching[J]. China Journal of Highway and Transport, 2007,20(6): 453 -558. |
| [9] | 司徒炳强,靳文舟.合作与竞争条件下公交网络发车时间优化模型[J].公路交通科技, 2010,27(6):122-128. SITU Bing-qiang, JIN Wen-zhou. Research on Timetable Optimization Model for Transit Network in Cooperation and Competition[J]. Journal of Highway and Transportation Research and Development, 2010,27(6):122-128. |
| [10] | 陈旭梅,林国鑫,于雷.常规公共交通与轨道交通运营调度协调模型[J].系统工程理论与实践,2009,29(10):165-173. CHEN Xu-mei, LIN Guo-xin, YU Lei. Modeling Operation Scheduling Coordination between Urban Rail System and Bus System[J]. Systems Engineering-Theory & Practice, 2009, 29(10):165-173. |
| [11] | 宗芳,往琳虹,贾洪飞.综合客运枢纽内各方式协调调度模型[J].华南理工大学学报: 自然科学版,2010,38(3):53-58. ZONG Fang, WANG Lin-hong, JIA Hong-fei. Coordinated Scheduling Model of Traffic Modes in Comprehensive Passenger Transport Hub[J]. Journal of South China University of Technology: Natural Science Edition,2010,38(3):53-58. |
| [12] | 刘小龙.细菌觅食优化算法的改进及应用[D]. 广州: 华南理工大学,2011. LIU Xiao-long. Improvement and Application of Bacterial Foraging Optimization Algorithm[D]. Guangzhou: South China University of Technology, 2011. |
| [13] | 《现代应用数学手册》编委会.现代应用数学手册:运筹学与最优化理论卷[M].北京: 清华大学出版社,2004. Editorial Board of Modern Applied Mathematics Editorial Handbook. Modern Applied Mathematics Handbook: Operations Research and Optimization Theory [M]. Beijing: Tsinghua University Press, 2004. |
 2015, Vol. 31
2015, Vol. 31

 ,
,