扩展功能
文章信息
- 赵全满, 张洪亮, 高江平, 郭桂宏
- ZHAO Quan-man, ZHANG Hong-liang, GAO Jiang-ping, GUO Gui-hong
- 基于平整度的CRCP冲断区域维修标准研究
- Study on Maintenance Standard of CRCP in Punch-out Area Based on Roughness
- 公路交通科技, 2015, Vol. 31 (4): 130-135
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (4): 130-135
- 10.3969/j.issn.1002-0268.2015.04.023
-
文章历史
- 收稿日期:2014-01-08
连续配筋混凝土路面(CRCP)具有行车舒适、使用寿命长和养护要求低等优点,在国外现已大量用于干线公路和机场,具有广阔的应用前景。CRCP的主要病害形式为冲断,AASHTO 2002设计指南[1]中以冲断和平整度作为CRCP的基本设计指标。冲断[2]是指由两个间距很小(小于0.6 m)的横向裂缝与较短的纵向裂缝和路面边缘(或纵向接缝)所围成,并发生了影响行车舒适性和安全性的严重碎裂或裂缝剥落的区域。冲断的发展过程以纵向裂缝的形成时刻为界分成两个阶段,第1阶段是纵向裂缝的形成阶段,见图 1(a);第2阶段是由横向裂缝、纵向裂缝和路面边缘(或纵向接缝)形成的区域褪化,见图 1(b)。冲断区域若仅出现纵向裂缝处于第1阶段,则很长时间内对于行车舒适性基本没有影响。只有冲断继续褪化进入第2阶段才会严重影响行车舒适性和安全性。

|
| 图 1 CRCP冲断Fig. 1 Punch-out of CRCP |
第2阶段冲断区域会降低驾驶员和乘客的行车舒适性,同时车辆的振动有可能使车辆脱离地面导致安全事故,因而需要对路面进行维修。但第2阶段冲断发展到什么程度需要维修,目前尚未见相关研究。冲断问题主要是路面结构破坏问题,路面结构的破坏进而导致路面平整度发生变化。目前,国际上应用最为常用的平整度评价指标是IRI。在AASHTO2002[1]中和绝大多数欧洲国家都采用IRI作为平整度评价指标[3],但研究发现IRI作为平整度评价指标与行车舒适性关系较差[4, 5, 6, 7]。
国内一些学者[8, 9, 10, 11, 12]建立了车辆振动模型对路面问题进行研究。陶向华[8]建立了车辆振动模型对路面平整度问题进行研究,分析了加速度与行车舒适性的关系。杨万桥[9, 10]建立了三自由度和五自由度车辆振动模型对路面平整度问题进行了研究,并以加权加速度均方根值为车辆行车舒适性评价指标。但是存在以下问题:(1)车辆在路面上行驶时,路面会随着车辆一块振动,目前建立的车辆振动模型只考虑了人和车的振动,而忽略了道路的振动;(2)冲断区域属于局部平整度问题,而目前研究多为较长区域的平整度问题,与冲断区域的局部平整度问题不同。张洪亮[11]建立了车辆振动模型,对路桥过渡段容许沉降问题进行了研究。郑木莲[12]通过试验方法获得乘客竖向加速度,并对行车舒适性进行研究。桥头跳车问题虽为局部平整度问题,但是桥头的断面形式与冲断区域存在很大的不同,而且以上研究没有考虑道路的振动问题。因此,论文在考虑道路振动的基础上建立人-车-路耦合的四自由度振动模型,以最大瞬态振动值为评价指标对冲断区域维修标准进行研究。 1 人-车-路耦合振动模型的建立和求解 1.1 人-车-路耦合振动方程的建立
为了探究驾驶员及乘客在道路上的行车舒适性,目前,经常采用简化的三自由度车辆振动模型[13],该模型可以很好地代表连续式不平整度仪中的测试轮模型。而且,文献[13]已经证明:在车辆垂直振动响应的预测方面,将车辆简化成三自由度体系是相当成功的。CRCR的冲断破坏导致路面平整度发生变化,因而可建立三自由度车辆振动模型对冲断问题进行研究。
考虑道路随车辆一起振动,论文在三自由度人-车振动模型的基础上,建立了人-车-路耦合的四自由度振动模型,对连续配筋混凝土路面的冲断问题进行研究。四自由度人-车-路模型如图 2所示,车辆行车方向如图所示,其中各阻尼和弹簧均视作线性的。图中k′1,k′2,k′3和k′4分别为座椅、悬挂系统、轮胎和路面结构的刚度系数;c′1,c′2,c′3和 c′4 分别为座椅、悬挂系统、轮胎和路面结构的阻尼系数;m1为人和座椅的质量和;m2为车体与装载物的质量总和的1/4;m3为车轮质量;m4为单位长度路面结构的质量。以该四自由度体系在基准面上达静力平衡时m1,m2,m3和m4的中心所在位置分别作为坐标轴y1,y2,y3和y4的原点,方向以向下为正。y1,y2,y3,y4和ξ分别为座椅、车架、轮胎、路面结构和路基的位移坐标,另取路面纵坡坡度为θ,车速为v,冲断区域台阶高度为u。
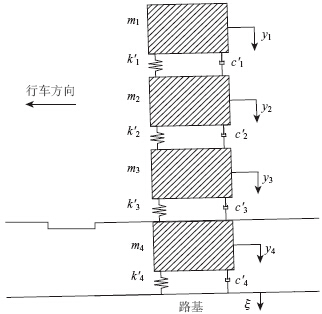
|
| 图 2 人-车-路耦合振动系统模型Fig. 2 Human-vehicle-road coupled vibration system model |
根据人-车-路耦合振动模型建立的振动方程见式(1)~式(4)。
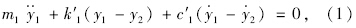
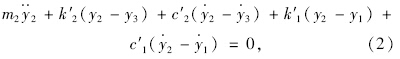
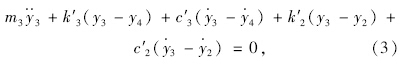
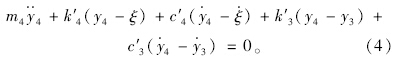
振动模型建立后,振动方程的求解是一个亟需解决的问题。求解振动方程有很多种方法,可以采用数值方法,常见的数值方法包括传递矩阵法[9, 10]、拉普拉斯变换法[11]、Wilson-θ法[14, 15]、New mark-β[16, 17]法、状态位移矩阵法[18, 19]、复数解法[20]和傅里叶变换法[21]等求解方程。在上述提到的解法中,Wilson-θ法只有当θ值较小时,计算精度才较好,可较好地控制误差范围;New mark-β法计算精度高,但其振幅衰减效果不好。国际平整度指数在研究中采用传递矩阵法进行计算时计算十分简单,应用范围广,本文采用传递矩阵法对振动方程进行求解。
实际计算中假设路基并不随着路面结构一起振动,认为路基振动位移和速度为0,即ξ和ξ·始终为0,将式(1)~式(4)两边同时除以m4可得式(5)~式(8)。
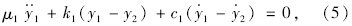
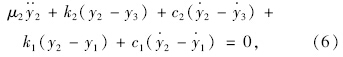
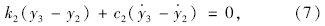
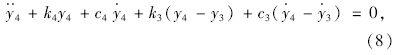
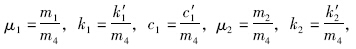
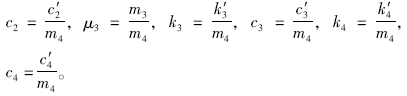
令向量Q(t)=[y1 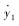 y2
y2 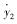 y3
y3 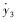 y4
y4 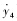 ]T,则式(5)~式(8)可写成式(9):
]T,则式(5)~式(8)可写成式(9):
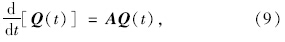
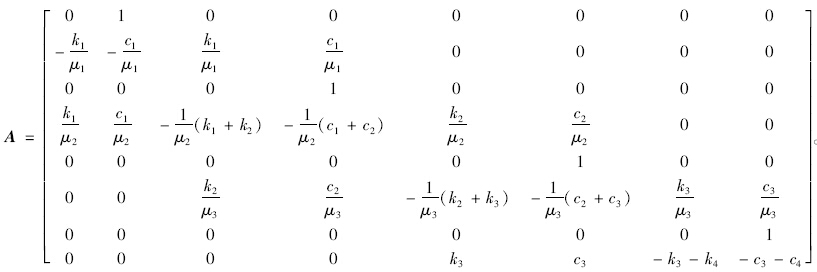
结合初值条件,求解微分方程式(9),得式(10),
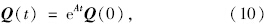
对式(10)求导得到式(11):
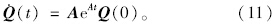
根据振动模型的初始条件,求解式(10)即可得到向量Q(t) 的值,即得到各质量的位移值和速度值,进而求解式(11)得到各质量的加速度值和速度值,即可得到乘客加速度值。 1.3 初始条件的确立
当车辆进入冲断区域时,以车辆刚好未进入冲断区域时为零时刻,以冲断区域路面为基准面,则振动模型的初始条件见式(12):
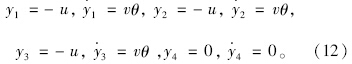
当车辆离开冲断区域时,以车辆刚好离开冲断区域进入路面为初始时刻,以冲断区域的水平面为基准面。当车辆刚驶离冲断区域时除车辆轮胎外其余各质量来不及反应,因而除轮胎初始位移外(轮胎的初始位移与冲断区域台阶高度进行叠加),各质量的初始位移、速度和加速度以车辆进入冲断区域时计算的相应时刻计算值为准。设相应时刻轮胎位移计算值为a,则车辆离开冲断区域时轮胎位移的初始条件为a-u,以此为初始条件,根据式(11)对乘客加速度进行求解。 1.4 乘客加速度值的求解
根据式(11),结合人-车-路耦合振动的初始条件和相关参数,运用Matlab软件对振动模型进行编程,计算乘客加速度值。计算所需要的参数主要包括汽车的参数、路面结构参数、车速和道路纵坡等。参考相关文献[11],人-车-路耦合振动模型的计算参数取为: m1=46,m2=4×103,m3=480,m4=3.5×104, k′1=2 100,k′2=95×104,k′3=48×104, k′4=6×106,c′1=1800,c′2=7×103, c′3=5×103,c′4=5×104。
冲断区域的台阶高度取u=0.01 m,初始冲断区域的大小为0.6 m×0.6 m;路面纵坡取值为取θ=2%;汽车行进方向为下坡方向,车速为v=30 km/h。由汽车的参数、路面结构参数、车速和道路纵坡等条件可知初始条件Q(0)=(-0.01,0.166 7,-0.01,0.166 7,-0.01,0.166 7,0,0)T,在冲断区域行驶时间为0.072 s,然后驾离冲断区域。利用Matlab编程计算所得乘客加速度随时间的变化如图 3所示。
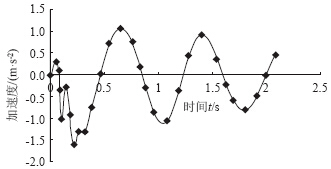
|
| 图 3 乘客加速度随时间的变化Fig. 3 Passenger's acceleration varying with time |
根据计算结果和图 3可知:当车辆经过冲断区域时,乘客加速度随时间的变化而上下波动,呈衰减振动,但其振幅逐渐减小,说明乘客的行车不舒适性随着时间的推移逐渐消失。当车辆经过冲断区域0.22 s时乘客加速度绝对值最大,为1.57 m/s2,实际为负值即乘客有超重感,说明在此刻乘客感觉最不舒服。 1.5 乘客行车舒适性的评价
车辆经过道路的冲断区域时,会引起车辆的振动,进而降低车辆的舒适性,也有可能会引起车辆的失控,进而影响行车的安全性。因此需从汽车行驶的舒适性和安全性两个方面来考虑,两者中舒适性要求更为严格,故而从舒适性角度来评价。
ISO 2631-1—1997 以加权加速度均方根值作为行驶舒适性的基本评价指标,并引入“总乘坐值法”给出了加速度均方根值与人体舒适程度的关系[22],见表 1。
| 加权加速度均 方根值/(m·s-2) |
人体舒适 程度 |
加权加速度均 方根值/(m·s-2) |
人体舒适 程度 |
| <0.315 | 保持舒适 | 0.315~0.63 | 稍不舒适 |
| 0.5~1 | 有些不舒适 | 0.8~1.6 | 不舒适 |
| 1.25~2.5 | 非常不舒适 | >2 | 特别不舒适 |
加权加速度均方根值计算公式为:

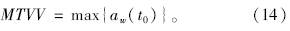
计算MTVV时,τ建议选用1 s(当加速度绝对值第1次达到最大时开始计时)。根据1.4节求得乘客加速度并结合式(13)和式(14)求得MTVV为0.85 m/s2,根据表 1的标准,此时驾驶员和乘客舒适程度为有些不舒适。由于冲断区域所引起的汽车振动持续的时间很短,是典型的瞬态振动,因此采用最大瞬态振动值作为乘客行车舒适性评价控制指标是可行的。 2 确定冲断区域维修标准的方法和步骤
本节基于前文研究成果给出CRCP冲断区域维修标准的确定方法和步骤,并给出相应算例。 2.1 方法和步骤
研究表明,车辆参数、载重、行车速度、冲断区域台阶高度和路面纵坡坡度等对乘客加速度和最大瞬态振动值影响较大,进而影响冲断区域维修标准的确定,因而确定混凝土路面冲断区域维修方法和步骤如下:
(1)汽车模型和结构参数的确定
标准车辆主要与公路的等级和用途有关。二级及二级以下公路,或以运煤等运货为主要目的公路,宜以载重汽车作为标准车辆;高速公路和一级公路以行驶小汽车为主,宜以小汽车作为标准车辆。标准车辆确定以后,可从汽车厂家取得汽车的结构参数。
(2)确定载重
汽车空载时振动更大,因此尽管重车通过冲断区域时更容易出事故,由于舒适性比安全性更严格,因此确定冲断区域维修标准时应采用空载时的汽车,这样计算出来的结果才会偏于安全。
(3)确定行车速度
建议以各级公路的设计速度作为计算速度。
(4)确定冲断区域台阶高度
用3 m直尺或其他平整度测试仪作为测量工具,测出混凝土路面冲断区域台阶高度,取冲断区域及冲断区域前后段路面的最大高差。
(5)确定纵坡坡度
建议以各级公路的设计纵坡为计算纵坡。
(6)确定引道路基路面的刚度和阻尼系数
对于具体某一连续配筋混凝土路面,可通过试验测定路面的刚度系数和阻尼系数。
(7)确定标准最大瞬态振动值
标准最大瞬态振动值的确定首先取决于容许振动标准的确定,不同等级的公路对舒适性的要求不同,可分别提出不同的标准最大瞬态振动值。本文建议以不舒适作为路面维修标准,具体舒适性评价参考表 1。
(8)确定路面是否需要维修
根据汽车结构参数、载重、设计车速、设计纵坡、台阶高度、路面刚度和阻尼系数等参数,计算出MTVV,然后将计算值与所定标准值进行对比,确定路面是否需要维修。 2.2 算例
假设某一城市道路,设计速度为30 km/h,路面纵坡为2%,利用3 m直尺测得冲断区域台阶高度为2 cm,假定标准车辆和路面相应参数(通过试验获得)与前文相同,则CRCP冲断区域维修标准的计算步骤如下:
(1)汽车模型和结构参数的确定。选择标准车辆与前文相同,具体参数参考前文。
(2)确定载重。因选择空载计算结果更偏于安全,因而选择车辆空载,即不计车辆载重。
(3)确定车速。根据路面情况,设计车速为30 km/h,选择其为计算速度。
(4)确定冲断区域台阶高度。用3 m直尺测得冲断区域台阶高度为2 cm。
(5)确定路面纵坡。根据路面情况,路面设计纵坡为2%,选择其为计算纵坡。
(6)确定引道路基路面的刚度和阻尼系数。根据试验获得路面刚度和阻尼(假定与前文相同)。
(7)确定标准最大瞬态振动值。其为城市道路,对路面行车舒适性要求较高,参考表 1,以行车不舒适作为路面需要维修的标准,即加权加速度均方根大于0.8 m/s2,安全起见取小值时路面需要维修。
(8)确定路面是否需要维修。根据前文的振动模型并结合相应参数,计算所得的MTVV为1.09 m/s2,大于0.8 m/s2,因而路面需要维修 3 结论
本文首先建立了冲断区域人-车-路耦合振动模型和振动方程,然后运用传递矩阵法对振动方程进行求解,结合初值条件运用Matlab软件计算得到乘客加速度和最大瞬态振动值,并得出如下结论:
(1)通过计算发现:一定条件下,乘客加速度最大值并不是发生在车辆经过冲断区域时,而是发生在经过冲断区域0.22 s之后。
(2)考虑行车舒适性,以国际标准ISO 2631-1—1997中的最大瞬态振动值为评价指标,给出了冲断区域维修标准的确定方法和步骤,并给出了相应算例,为路面维修提供一定的依据。
(3)本文从理论角度对冲断区域维修标准进行研究,并以MTVV为行车舒适性评价指标,将来可进行相关试验以验证其合理性。
| [1] | MASON M. Guide for Mechanistic-empirical Design of New and Rehabilitated Pavement Structures,NCHRP 1-37A [R]. Washington,D. C.:Transportation Research Board,2004. |
| [2] | 左志武.连续配筋混凝土路面横向裂缝分布和冲断预估研究[D].西安:长安大学,2010. ZUO Zhi-wu. Study on Distribution of Transverse Cracks and Punch-out Prediction of Continuously Reinforced Concrete Pavement [D]. Xi'an:Chang'an University,2010. |
| [3] | 刘云,钱振东.路面平整度及车辆振动模型的研究综述[J].公路交通科技,2008,25(1):51-57. LIU Yun,QIAN Zhen-dong. Review of Road Roughness and Vehicle Vibration Model[J]. Journal of Highway and Transportation Research and Development,2008,25(1):51- 57. |
| [4] | PAPAGIANNAK A T,RAVEENDRANA B. International Standards Organization- compatible Index for Pavement Roughness [J]. |
| [5] | AWASTHI G,SINGH T. Roughness of Pavement Surfaces[D]. Kanpur:Indian Institute of Technology Kanpur,2001. |
| [6] | ASTM STP929,The Tire Pavement Interface [S]. |
| [7] | TODD K B,KULAKOWSKI B T. Simple Computer Models for Predicting Ride Quality and Pavement Loading for Heavy Trucks[J]. Transportation Research Record,1989,1215:137-150. |
| [8] | 陶向华,黄晓明.人-车-路相互作用三质量车辆模型分析[J].交通运输工程学报,2004,4(3):11-15. TAO Xiang-hua,HUANG Xiao-ming. Three-mass Vehicle Model of People-vehicle-road Interaction[J]. Journal of Traffic and Transportation Engineering,2004,4(3):11-15. |
| [9] | 杨万桥. 基于人-车-路相互作用的沥青路面平整度评价方法研究[D].西安:长安大学,2009. YANG Wan-qiao. Research on Evaluation Method of Asphalt Pavement Roughness Based on Human-vehicle-road Interaction[D].Xi'an:Chang'an University,2009. |
| [10] | 张洪亮,王秉纲,杨万桥. 基于人-车-路三自由度振动模型的路面平整度评价方法[J].重庆交通大学学报:自然科学版,2009,28(6):1041-1045. ZHANG Hong-liang,WANG Bing-gang,YANG Wan-qiao. Pavement Roughness Evaluation Method Based on Three-degree-freedom Models Including Human,Vehicle and Road[J]. Journal of Chongqing Jiaotong University:Natural Science Edition,2009,28(6):1041- 1045. |
| [11] | 张洪亮. 路桥过渡段车路动力学分析及容许差异沉降研究[D]. 西安:长安大学,2003. ZHANG Hong-liang. Study on Dynamic Vehicle-road Interaction and Tolerable Differential Settlement at Road-bridge Transition Section [D]. Xi'an: Chang'an University,2003. |
| [12] | 郑木莲,孟建党,张世铎,等.路桥过渡段上车内人体舒适性评价方法[J].长安大学学报:自然科学版,2012,32(2):1-6. ZHENG Mu-lian,MING Jian-dang,ZHANG Shi-duo,et al. Evaluation Method of Human Comfort in Vehicle at Transition Section between Bridge Abutment and Embankment [J]. Journal of Chang'an University:Nature Science Edition,2012,32(2):1- 6. |
| [13] | 孙璐,邓学钧. 速度与车辆动态特性对于车路相互作用的影响[J]. 土木工程学报,1997,30(6):34-40. SUN Lu,DENG Xue-jun. The Influences of Speed and Dynamic Characteristics of Truck on Vehicle-pavement-road Interactions[J]. China Civil Engineering Journal,1997,30(6):34-40. |
| [14] | 宋一凡,陈榕峰.基于路面不平整度的车辆振动响应分析方法[J].交通运输工程学报,2007,7(4):39- 43. SONG Yi-fan,CHEN Rong-feng. Analysis Method of Vehicle Vibration Response Caused by Pavement Roughness[J]. Journal of Traffic and Transportation Engineering,2007,7(4):39-43. |
| [15] | 刘晓明,赵明华,黎大志.基于整车模型的桥头路面动力荷载分析[J].公路交通科技,2007,24(7):39- 43. LIU Xiao-ming,ZHAO Ming-hua,LI Da-zhi. Analysis of Dynamic Force on the Bridge Approaches Pavement Based on Whole Vehicle Model[J]. Journal of Highway and Transportation Research and Development,2007,24(7):39- 43. |
| [16] | 吴庆雄,陈宝春,奚灵智.路面平整度PSD和IRI评价方法比较[J].交通运输工程学报,2008,8(1):36- 41. WU Qing-xiong,CHEN Bao-chun,XI Ling-zhi. Comparison of PSD Method and IRI Method for Road Roughness Evaluation [J]. Journal of Traffic and Transportation Engineering,2008,8(1):36-41. |
| [17] | 韩万水,陈艾荣. 杭州湾跨海大桥车桥空间耦合振动参数分析[J]. 公路交通科技,2008,25(5):56- 61. HAN Wan-shui,CHEN Ai-rong. Parametric Analysis of Three-dimensional Coupling Vibration for Hangzhou Bay Bridge[J]. Journal of Highway and Transportation Research and Development,2008,25(5):56-61. |
| [18] | SAYERS M W,GILLESPIE T D,QUEIROZ A V. The International Road Roughness Experiment:Establishing Correlation and a Calibration Standard for Measurements,HS-039 586[R]. Washington,D.C.:World Bank,1986. |
| [19] | AWASTHI G,SINGH T,DAS A. On Pavement Roughness Indices[J]. Journal of the Institution of Engineers,2003,84(1):33-37. |
| [20] | 于清.路面平整度与车辆动荷载关系的研究[D].重庆:重庆交通学院,2004. YU Qing. Research on Relationship between Pavement Evenness and Vehicle Dynamic Load[D]. Chongqing:Chongqing Jiaotong Institute,2004. |
| [21] | 郭成超,陶向华,王复明.车速和路面不平度特性对车路相互作业的影响[J].华北水利水电学院学报,2004,25(3):42- 45. GUO Cheng-chao,TAO Xiang-hua,WANG Fu-ming. The Influence of Vehicle Speed and Pavement Roughness Characteristics on Vehicle-road Interaction[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power,2004,25(3):42- 45. |
| [22] | ISO-2631—1997,Mechanical Vibration and Shock-Evaluation of Human Exposure to Whole-body Vibration-Part l:General Requirement[S]. |
 2015, Vol. 31
2015, Vol. 31

 ,
,