扩展功能
文章信息
- 刘伟, 肖文彬, 高显鹏
- LIU Wei, XIAO Wen-bin, GAO Xian-peng
- 交叉口流线动态控制的优化配时模型研究
- Research of Optimal Timing Model Based on Dynamic Control of Traffic Flow at Intersection
- 公路交通科技, 2015, Vol. 31 (4): 124-129,142
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (4): 124-129,142
- 10.3969/j.issn.1002-0268.2015.04.022
-
文章历史
- 收稿日期:2014-06-26
随着城市交通拥堵越来越严重,交通供需矛盾日益突出,挖掘已有路网的潜力,提高交通供给是交通管理的重要手段。近年来利用智能交通技术对交通网络通行能力的提高起到了很大的作用。交叉路口作为城市道路交通的主要集散点,是交通拥堵的主要发生节点。智能交通控制系统对城市交叉口运行控制主要体现在对路口流量的自适应优化和交叉口之间的协调运行方面。对交叉路口交通流线进行合理的分析、动态组合和智能信号控制,可缓解城市交通的节点拥堵,提升路网的运行效率。
城市交叉口信号控制的优化研究,最初是在一定周期条件下对控制方案进行优化[1, 2],后来采用不同的方法来优化配时控制[3, 4, 5]。这个研究阶段的动态控制是建立在固定相位相序的基础上的,未考虑流线动态组合变化的重要性,且配时模型只针对饱和或非饱和的单一交通状态。随后以车辆平均延误时间为控制目标,采用模糊控制器和相序优化器联合进行交通控制[6],研究了信号控制相位相序的优化。在因相位相序安排不适应造成的交叉口时空资源损失和事故隐患越来越多的情况[7]以及多相位优化控制方法的研究[8, 9, 10]中对于单个交叉口相位变化周期的控制[11, 12, 13],其控制过程较为复杂,未引用交通流线相容性组合,可行组合数较少,没有结合动态最优控制进行配时。
本文提出一种新的相容流线搜索方法,得到一种更加简便、更加直观的流线相容图,从而更加简便地确定流线动态最优组合。但随着车联网、车路协同及交叉口数据采集技术的不断发展与运用,能够动态获取交叉口各进口流线车辆到达参数,从而为交叉口相位流线动态组合优化控制的实现提供条件。该研究也是基于交通信息检测技术发展的前瞻性而提出的优化控制方法,伴随着城市道路交通的智能化,具有应用前景。该研究旨在综合交叉口饱和与非饱和两种状态,根据动态获取的各流线到达率建立改进的延误最小配时模型,确定相位最优配时,以最大限度降低车辆行程延误,提高交叉口控制效率。 1 计算相容流线确定最优组合
寻求单点交叉口的流线最优组合,必须了解交叉口各交通流线的交通特性,并根据其特性确定交通流之间的相容关系。因此,引入交通流相容的概念,即各交通流在无冲突条件下能够同时获得通行权的一系列流线搭配[14]。
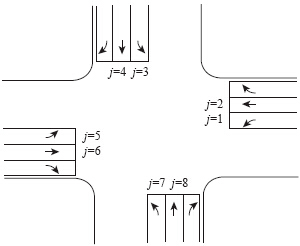
本文以典型交叉口的四相位最优控制为例,交叉口每个进口有3条车道,分别为左转、直行、右转车道,则每个交叉口共有12股交通流线。因我国采用的是右行制,右转交通流线对整个交叉口的影响较小,所以对右转流线不作考虑。将检测线圈布设于直行、左转车道,具体交叉口布局形式见图 1。
|
| 图 1 典型交叉口交通流线图Fig. 1 Typical intersection traffic flow lines |
对交叉口各股交通流线采用符号σi,jl表示。其中,l为当前周期;i为相位序号,取值为1,2,3,4,分别表示交叉口一个周期内的4个相位;j为交通流线序号,取值为1,2,3,4,5,6,7,8,分别表示交叉口入口交通流向为东左(东行左转)、东直(东向直行)、北左、北直、西左、西直、南左、南直方向。如σ2,56表示的是第6周期自西向东左转进口流线作为第2相位放行。
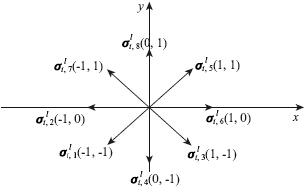
为了更直观地确定两股交通流线的相容关系,本文提出一种数学方法求解相容流线。即将8股交通流置于平面直角坐标系下,并将各流线采用向量表示,见图 2。
|
| 图 2 交通流线向量表示图Fig. 2 Representation of traffic flow line vectors |
根据向量运算法则,两非零向量a=(x1,y1)与b=(x2,y2)的数量积(点乘)计算公式为:
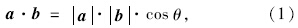
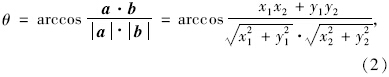
由交通流线相容性定义,可知某交通流线的相容流线具有如下规律:
(1)两向量共线则必相容;
(2)两向量之间的夹角为45°时,其所对应的交通流向必相容。
根据以上两条规律,可知任一交通流线有3股相容流线。交叉口控制过程中,一般不采用1股流线构成1个相位,否则会导致控制过程绿灯损失增大。采用两两组合,通过向量运算,8股交通流线可分为12组,用A1至A12表示,见表 1。
| 完全 相容 |
交通流线 序号 |
分流 相容 |
交通流线 序号 |
合流 相容 |
交通流线 序号 | |||
| A1 | σli,1 | σli,5 | A5 | σli,1 | σli,2 | A9 | σli,1 | σli,4 |
| A2 | σli,2 | σli,6 | A6 | σli,3 | σli,4 | A10 | σli,3 | σli,6 |
| A3 | σli,3 | σli,7 | A7 | σli,5 | σli,6 | A11 | σli,5 | σli,8 |
| A4 | σli,4 | σli,8 | A8 | σli,7 | σli,8 | A12 | σli,2 | σli,7 |
为确定相位最优流线组合,引入相位绿灯损失概念。所谓相位绿灯损失指某相位绿灯时,该相位两股流线中的一流向车辆以饱和流率通过,而另一流向车辆以非饱和流率通行,此时说明绿灯时间未得到最大化利用,从而造成了绿灯时间的损失。
因此,要使周期绿灯损失降低到最小,应将各相容且流量相近的流线组合为1个相位,从而使相位流线组合达到最优。 2 相位最优配时模型
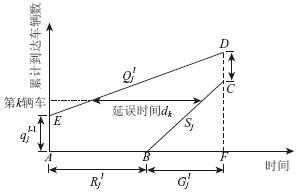
确定交叉口流线最优组合形式后,以车辆平均延误最小为目标,建立新的单点信号控制交叉口周期优化配时模型。当某一流线绿灯放行后,有车辆要进行二次排队,即图 3中qjl>0时,则对该流向进行延误分析,可得到当前周期延误计算模型:
|
| 图 3 车辆滞留流线平均延误模型Fig. 3 Model of average delay of traffic flow line with detained vehicle |
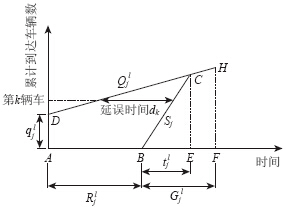
图 3中,A点对应红灯起始时刻,B点对应绿灯起始时刻,F点对应绿灯结束时刻。射线ED的斜率为车辆到达率Qjl,射线BC的斜率为进口道饱和流量Sjl。dk为第k辆车的延误时间。此时,第l周期结束后第j流线滞留车辆数qjl为:
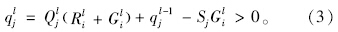
由该图的几何意义可知,五边形ABCDE的面积为流向j通过车辆的总延误。因此流线j通行车辆的平均延误为:
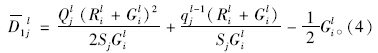
同理,当某一流线绿灯放行后,没有车辆要进行二次排队,即qjl=0时,延误模型(图 4)如下:
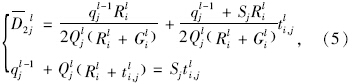
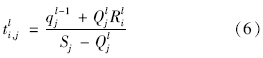
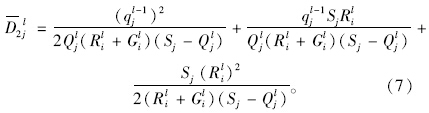
|
| 图 4 无车辆滞留流线平均延误模型Fig. 4 Model of average delay of traffic flow line without detained vehicle |
此时qjl=0,而Qjl(Ril+Gil)+qjl-1-SjGil≤0。
上述式中,ti,jl为第l周期第i相位初始时刻第j车道上车辆消散所需的时间;qjl-1为交叉口j流线在第(l-1)周期的滞留车辆数;Qjl为第l周期第j进口车道车辆的到达率;Gil为第i相位l周期的有效绿灯时间;Ril为第i相位l周期的红灯时间;Sj为进口道j的饱和流率。
综合考虑相位绿灯放行结束后某一流线有无第二次排队的情况,将上述两模型结合,得到如下适用性更为广泛的最优配时组合模型。
目标函数:
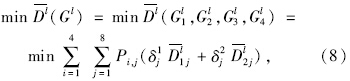
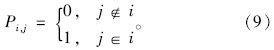
δj1和δj2的取值为0或1,但δj1≠δj2。当δj1=1,δj2=0时,表示qjl>0,即流向j在l周期绿灯结束时有车滞留;当δj1=0,δj2=1时,表示qjl=0,即流向j在l周期绿灯结束时无车滞留,且有:
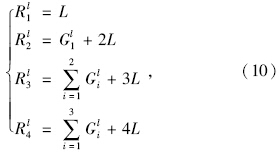

最小绿灯时间应允许所有介于停车线和检测器之间排队的车辆都能进入交叉口。因此有:
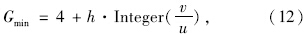
对于最大绿灯时间Gmax的设定:在假设采用定时式信号控制之下,计算最佳周期以及每个相位的绿灯时间,则最大绿灯时间为计算所得绿灯时间的1.25倍或1.5倍[15, 16]。 3 模型求解算法
为了便于算法的描述,对上述模型进行简化。数学模型和约束条件如下:
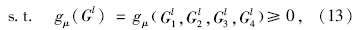
求解约束优化问题,就是要在可行域
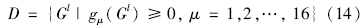
显然,约束函数gμ(Gl)为自变量Gl的线性函数,而目标函数Dl(Gl) 中自变量Gl最高次为二次,所以目标函数为自变量的非线性函数,因此模型为非线性规划的模型,对应优化问题为非线性优化问题。从约束条件的形式可以看出,其可行域 D={Gl|gμ(Gl)≥0,μ=1,2,…,16}为凸集,延误函数D1jl,D2jl是自变量G1l,G2l,G3l,G4l在可行域D内的凸函数。
目标函数Dl(Gl)中参数Pi,j,δj1,δj2都是0或1的函数,是常量,为函数D1jl,D2jl的线性组合。根据凸函数的性质,由两个在定义域D上的凸函数线性组合而成的函数在定义域D上也为凸函数,由此可以得知目标函数 Dl(Gl)为凸函数。
因处理约束条件的办法不同,约束优化方法也可分为直接法和间接法两大类。本文采用间接法中的内点罚函数法求解最优解。间接法的基本思想是将约束优化问题首先转换为一系列无约束优化问题,然后利用无约束优化方法来求解,逐渐逼近约束问题的最优解。
首先确定一组(δj1,δj2)的取值确定原目标函数,再构造如下增广目标函数:
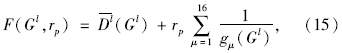
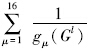 为障碍函数。
为障碍函数。
分析F(Gl,rp)是否符合内点罚函数法的构造设想。显然F(Gl,rp)和Dl(Gl)都定义在D内,rp取值较小时,当迭代点远离边界,F(Gl,rp)≈Dl(Gl),此时F(Gl,rp) 的最优解可作为上述模型的近似最优解;但当迭代点靠近D的边界时,由F(Gl,rp) 的构造知,即使rp取值很小,但gμ(Gl)→0,即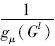 →+∞,使得F(Gl,rp)的函数值很大,此时显然不可能在区域D的边界附近求得F(Gl,rp)的最优解,于是迫使迭代点被阻挡,回到远离区域D的边界去寻优。用式子表示即是当障碍因子r1>r2>…>rp>…>0逐渐减小时,有:
→+∞,使得F(Gl,rp)的函数值很大,此时显然不可能在区域D的边界附近求得F(Gl,rp)的最优解,于是迫使迭代点被阻挡,回到远离区域D的边界去寻优。用式子表示即是当障碍因子r1>r2>…>rp>…>0逐渐减小时,有:
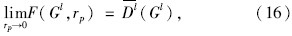
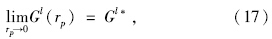
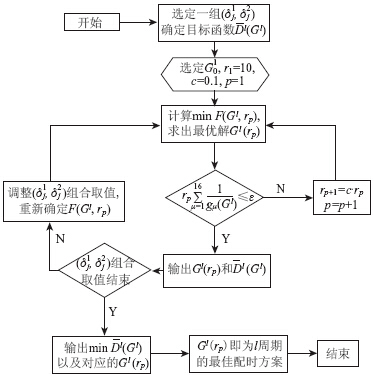
算法具体步骤见图 5。
|
| 注:ε为给定的足够小的正数;rp为障碍因子,初始p=1;c为障碍因子的缩小系数 图 5 模型求解算法流程图Fig. 5 Flowchart of model solution algorithm |
综上所述,在已知当前周期最优流线组合的基础上,通过算法求解延误组合模型,确定当前周期各相位的最优配时。由模型中考虑的上一周期滞留车辆数,可实现周期间的动态最优控制。
4 实例分析
以重庆市某典型交叉口为例,现阶段采用的是固定相序控制,检测线圈检测到各周期流线的车辆到达率见表 2。
| 周期 | 交通流线到达率/(veh·s-1) | |||||||
| j=1 | j=2 | j=3 | j=4 | j=5 | j=6 | j=7 | j=8 | |
| 1 | 0.220 | 0.189 | 0.191 | 0.178 | 0.118 | 0.168 | 0.163 | 0.177 |
| 2 | 0.087 | 0.129 | 0.057 | 0.126 | 0.085 | 0.124 | 0.144 | 0.081 |
| 3 | 0.105 | 0.081 | 0.087 | 0.083 | 0.067 | 0.134 | 0.145 | 0.166 |
| 4 | 0.065 | 0.062 | 0.103 | 0.120 | 0.075 | 0.084 | 0.064 | 0.110 |
| 5 | 0.135 | 0.092 | 0.188 | 0.157 | 0.127 | 0.136 | 0.127 | 0.159 |
| 6 | 0.086 | 0.135 | 0.105 | 0.148 | 0.125 | 0.147 | 0.052 | 0.150 |
| 7 | 0.059 | 0.069 | 0.127 | 0.095 | 0.088 | 0.132 | 0.083 | 0.075 |
| 8 | 0.158 | 0.173 | 0.127 | 0.221 | 0.193 | 0.141 | 0.183 | 0.197 |
| 9 | 0.124 | 0.143 | 0.153 | 0.042 | 0.087 | 0.105 | 0.164 | 0.043 |
| 10 | 0.201 | 0.108 | 0.124 | 0.137 | 0.129 | 0.069 | 0.119 | 0.123 |
| 11 | 0.068 | 0.162 | 0.119 | 0.216 | 0.132 | 0.134 | 0.100 | 0.125 |
| 12 | 0.128 | 0.064 | 0.045 | 0.050 | 0.115 | 0.121 | 0.065 | 0.057 |
| 13 | 0.084 | 0.125 | 0.126 | 0.094 | 0.148 | 0.118 | 0.143 | 0.095 |
| 14 | 0.106 | 0.105 | 0.065 | 0.109 | 0.076 | 0.090 | 0.139 | 0.147 |
| 15 | 0.143 | 0.149 | 0.152 | 0.097 | 0.139 | 0.124 | 0.146 | 0.142 |
| 16 | 0.165 | 0.114 | 0.184 | 0.135 | 0.090 | 0.110 | 0.126 | 0.119 |
| 17 | 0.089 | 0.154 | 0.124 | 0.138 | 0.106 | 0.124 | 0.165 | 0.153 |
| 18 | 0.036 | 0.067 | 0.086 | 0.173 | 0.065 | 0.169 | 0.069 | 0.129 |
| 19 | 0.145 | 0.128 | 0.088 | 0.047 | 0.156 | 0.109 | 0.139 | 0.106 |
| 20 | 0.158 | 0.137 | 0.127 | 0.130 | 0.129 | 0.051 | 0.142 | 0.161 |
该交叉口现阶段采用的是固定四相位控制,经常发生交通拥堵,交通流稳定性差,造成较大延误。
运用流线动态控制优化模型对其进行控制改善,交叉口左转流线的饱和流率为0.501 veh/s,直行流线饱和流率为0.528 veh/s;相位的最小绿灯时间Gmin为8 s;相位的最大绿灯时间Gmax为60 s;对20个周期的车辆到达率进行计算,得到各周期最佳流线组合、相位最佳配时以及周期平均延误,见表 3。
| 周期 | 最优流线组合 | 最优配时/s | 周期时 长/s |
周期平均 延误/s |
||||||
| i=1 | i=2 | i=3 | i=4 | G1l* | Gl*2 | Gl*3 | Gl*4 | |||
| 1 | A5 | A6 | A8 | A7 | 8 | 11 | 15 | 20 | 54 | 13 |
| 2 | A5 | A6 | A8 | A7 | 24 | 23 | 28 | 23 | 98 | 35 |
| 3 | A5 | A8 | A6 | A7 | 26 | 20 | 23 | 23 | 92 | 35 |
| 4 | A8 | A5 | A6 | A7 | 18 | 22 | 17 | 11 | 68 | 32 |
| 5 | A8 | A6 | A5 | A7 | 15 | 12 | 15 | 15 | 57 | 19 |
| 6 | A4 | A3 | A2 | A1 | 18 | 19 | 16 | 17 | 70 | 26 |
| 7 | A4 | A10 | A12 | A1 | 18 | 15 | 11 | 9 | 53 | 25 |
| 8 | A4 | A10 | A12 | A1 | 11 | 11 | 15 | 23 | 60 | 15 |
| 9 | A4 | A3 | A2 | A1 | 22 | 24 | 28 | 24 | 98 | 34 |
| 10 | A3 | A5 | A4 | A7 | 22 | 16 | 21 | 21 | 80 | 31 |
| 11 | A5 | A6 | A8 | A7 | 20 | 23 | 28 | 25 | 96 | 31 |
| 12 | A5 | A6 | A7 | A8 | 26 | 26 | 16 | 16 | 84 | 43 |
| 13 | A5 | A7 | A3 | A4 | 18 | 13 | 14 | 13 | 58 | 23 |
| 14 | A5 | A7 | A8 | A6 | 12 | 12 | 14 | 10 | 48 | 20 |
| 15 | A5 | A7 | A8 | A6 | 11 | 9 | 12 | 14 | 46 | 15 |
| 16 | A5 | A7 | A3 | A4 | 15 | 12 | 16 | 17 | 60 | 21 |
| 17 | A5 | A3 | A7 | A4 | 18 | 15 | 19 | 21 | 73 | 25 |
| 18 | A12 | A10 | A9 | A11 | 19 | 16 | 17 | 17 | 69 | 31 |
| 19 | A2 | A3 | A1 | A4 | 13 | 15 | 13 | 10 | 51 | 22 |
| 20 | A12 | A10 | A1 | A4 | 12 | 10 | 15 | 16 | 53 | 18 |
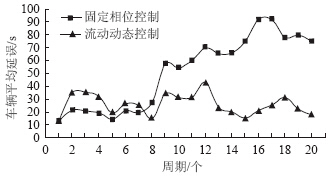
固定相位控制和流线动态组合控制方案下,对平均延误进行对比分析,见图 6。
|
| 图 6 延误对比分析图Fig. 6 Contrast analysis curves of delay |
通过对20个周期的平均延误计算,在定相位控制方案下,车辆平均延误为50 s/veh,流线动态控制优化方案的车辆平均延误为26 s/veh,车辆平均延误减少近一半。动态流线组合优化控制与交通流的随机变化协调性更好,显著地减少了行程延误,缓解了交通拥堵。 5 结论
交叉口采用固定相位和流线的控制方式,不能很好适应交通流较大、流线到达率不确定和随机性较大的交叉口,不能有效缓解交叉口的交通拥堵。只采用动态相位控制方式,无法根据流线的到达率调整相位组合,不能使交叉口运行状态达到最优。运用流线相容计算,结合流线的到达率,建立动态优化配时模型,可以实现交叉口各流线到达率随机状态下路口的优化控制,应用该方法对交叉口转向流线到达率随机性大的交叉口具有显著的改善效果。通过案例计算,可以减小一半左右的车辆平均延误。该优化方法也适用于T形交叉口的动态控制,后续的研究工作可加入行人流线进行综合考虑,以实现动态控制方法在交叉口控制方面的应用。
| [1] | ELAHI S M, RADWAN A E, GOUL K M. Knowledge-based System for Adaptive Traffic Signal Control[J]. Transportation Research Record, 1991,1324:115-122. |
| [2] | 高云峰,徐立鸿,胡华,等.交叉口定周期信号控制多目标优化方法[J].中国公路学报,2011,24(5):82-87. GAO Yun-feng,XU Li-hong,HU Hua,et al.Multi-objective Optimization Method for Fixed-time Signal Control at Intersection[J].China Journal of Highway and Transport,2011,24(5):82-87. |
| [3] | 首艳芳,徐建闽. 信号交叉口多目标动态决策模型及其优化方法[J]. 公路交通科技,2012,29(11):92-97. SHOU Yan-fang,XU Jian-min. Multi-objective Dynamic Decision-making Model of Signalized Intersection and Its Optimization Method[J]. Journal of Highway and Transportation Research and Development,2012,29(11):92-97. |
| [4] | 李明利,赵祥模,张利川. 基于排队状态的单点交叉口动态信号配时算法[J]. 交通运输工程学报,2008,8(5):100-103. LI Ming-li,ZHAO Xiang-mo,ZHANG Li-chuan. Dynamic Signal Timing Algorithm at Single-point Intersection Based on Queuing Condition[J]. Journal of Traffic and Transportation Engineering,2008,8(5):100-103. |
| [5] | 田丰,边婷婷. 基于自适应遗传算法的交通信号配时优化[J]. 计算机仿真,2010,27(6):305-308. TIAN Feng,BIAN Ting-ting. Traffic Signal Timing Optimization Based on Adaptive Genetic Algorithm[J]. Computer Simulation,2010,27(6):305-308. |
| [6] | 沈国江,孙优贤. 基于相序优化的多相位模糊交通控制[J].控制与决策,2002,17(增1):654-658. SHEN Guo-jiang, SUN You-xian. Multi-phase Fuzzy Traffic Control Based on Phase Sequencer[J]. Control and Decision,2002,17(S1):654-658. |
| [7] | 王浩,彭国雄,杨晓光. 相位相序安排与交叉口设计之间的关系[J]. 公路交通科技,2004,21(2):92-94. WANG Hao,PENG Guo-xiong,YANG Xiao-guang. The Relationship between Traffic Signal Phasing-Sequence and Intersection Geometry Design[J]. Journal of Highway and Transportation Research and Development,2004,21(2):92-94. |
| [8] | 赵忠杰,刘小强,谢光秋.单交通路口变相位变周期信号控制[J].长安大学学报:自然科学版,2005,25(6):70-72. ZHAO Zhong-jie, LIU Xiao-qiang, XIE Guang-qiu. Changeable Phases and Changeable Periods Signal Control at Traffic Intersection[J]. Journal of Chang'an University: Natural Science Edition, 2005,25(6):70-72. |
| [9] | 王莉,王明哲,周丰, 等. 实时自适应交通信号控制CPN建模分析[J]. 公路交通科技,2008,25(6):115-119. WANG Li,WANG Ming-zhe,ZHOU Feng,et al. Modeling and Analyzing of Real-time Adaptive Traffic Signal Control with CPN[J]. Journal of Highway and Transportation Research and Development,2008,25(6):115-119. |
| [10] | 高海军,李灵犀, 陈龙. 交通路口可变相位信号控制[J]. 交通运输工程学报,2003,3(3):79- 83. GAO Hai-jun, LI Ling-xi, CHEN Long. Changeable Phases Signal Control of Traffic Intersection[ J]. Journal of Traffic and Transportation Engineering, 2003,3(3):79-83. |
| [11] | 古柏利尼奇,森伯恩,拉基奇. 城市交通信号优化控制[M]. 张永忠, 等译. 北京:中国水利水电出版社,2012. GUBERINIC S,SCNBORN G,LAZIC B. Optimal Traffic Control Urban Intersections[M]. ZHANG Yong-zhong,et al translated. Beijing:China Water Power Press,2012. |
| [12] | 陈峻,张国良,徐良杰, 等.交通管理与控制[M].北京:人民交通出版社,2012. CHEN Jun,ZHANG Guo-liang,XU Liang-jie,et al. Traffic Management and Control[M].Beijing:China Communications Press,2012. |
| [13] | ZHENG X,RECKER W. An Adaptive Control Algorithm for Traffic-actuated Signals[J]. |
| [14] | 王殿海. 交通流理论[M].北京:人民交通出版社,2002. WANG Dian-hai. Traffic Flow Theory[M]. Beijing:China Communications Press,2002. |
| [15] | 黄永刚,温惠英,何兆成, 等. 基于Paramics的多相位感应信号控制仿真研究[J]. 交通与计算机,2007,25(6):45-48. HUANG Yong-gang,WEN Hui-ying,HE Zhao-cheng,et al. Simulation of Multi-phase Actuated Signal Control Based on Paramics[J]. Computer and Communications,2007,25(6):45-48. |
| [16] | 温凯歌,曲仕茄,张玉梅.城市单交叉口信号多相位自适应控制模型[J]. 系统仿真学报,2009,21(10):3066-3070. WEN Kai-ge,QU Shi-ru,ZHANG Yu-mei. Multiphase Traffic Signal Adaptive Controlling Model for Urban Isolated Intersection[J]. Journal of System Simulation,2009,21(10):3066-3070. |
 2015, Vol. 31
2015, Vol. 31

 ,
,