扩展功能
文章信息
- 易炳疆
- YI Bing-jiang
- 三主桁三索面斜拉桥索力横向分配计算简化
- Simplification of Transverse Distribution Calculation for Cable-stayed Bridge with 3 Main Trusses and 3 Cable Planes
- 公路交通科技, 2015, Vol. 31 (4): 95-101
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (4): 95-101
- 10.3969/j.issn.1002-0268.2015.04.017
-
文章历史
- 收稿日期:2014-05-30
三主桁梁桥主梁由3片主桁组成,横向由横梁、横联、平联等构件组成,而三主桁三索面斜拉桥是在三主桁梁桥的基础上,在每片主桁对应位置布置一面拉索形成的。
对于斜拉桥成桥状态,拉索不施加初拉力时,自重作用下两主桁斜拉桥横向两索面索力完全相等,而三主桁斜拉桥横向三索面索力则必须考虑横向分配的问题,边索、中索索力在横桥向不是简单的3倍或者2倍左右的关系(图 1~图 2),其差异随拉索刚度、主梁横向联接体系刚度、节点刚度等因素变化:纵向主要受主桁竖向刚度的影响,横向主要受横向联接体系刚度和拉索刚度的影响,最终索力是3种因素共同作用的结果。

|
| 图 1 中边支座反力呈10∶3关系Fig. 1 Ratio 10∶3 between side and middle support reactions |

|
| 图 2 中边支座反力呈2∶1关系Fig. 2 Ratio 2∶1 between side and middle support reactions |
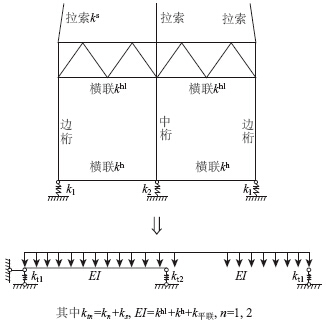
对三主桁斜拉桥进行分析时,可以近似地将其主梁横截面看成两跨弹性支承连续梁,梁的抗弯刚度为横梁和横联竖向刚度之和,弹性支承刚度由主桁竖向刚度和斜拉索刚度叠加而成,如图 3所示。
|
| 图 3 中边支座反力呈一定规律变化Fig. 3 Regular changes between side and middle support reactions |
在横向,三索面的最终索力大小与弹性支承刚度和主梁抗弯刚度的相对关系有关,当梁的抗弯刚度趋于无限小,或者弹性支承刚度趋于无限大时,拉索索力将呈10∶3关系,因此,图 1只是图 3的特殊情况。而当梁的抗弯刚度趋于无限大,或者支承刚度趋于无限小时,横向三索面索力将趋于相等。在纵向,拉索主要承担主桁传来的力,确切地说,在斜拉桥主梁节点横截面,主桁传给横截面框架的力是数个节点集中力,该集中力跟主桁单元两端节点的竖向位移关系有关。因此,计算主桁传给横向等效连续梁节点的集中力时,不能按照节点刚性支承情况的计算方法,每个节点受到的集中力等于一个节间荷载的1/2,如图 4所示,而应综合考虑主桁的竖向弹性支承刚度和节点竖向位移的作用,将每个节间荷载乘以一个适当的系数,该系数跟主桁竖向刚度、拉索刚度等有关,如图 5所示。

|
| 图 4 刚性支承条件下结构的纵向简化示意Fig. 4 Simplification of structure with rigid support in longitudinal direction |

|
| 图 5 弹性支承条件下主梁的纵向简化示意Fig. 5 Simplification of structure with elastic support in longitudinal direction |
1.1 横向力学推导
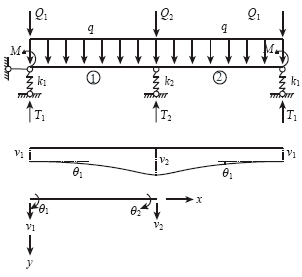
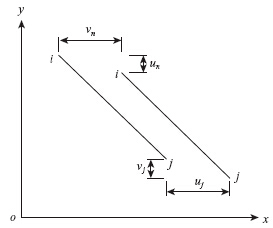
三主桁三索面斜拉桥在横向可近似模拟成两跨弹性支承连续梁,其中拉索和主桁为具有一定刚度的弹性支承,并假设在横梁上作用对称均布荷载q,①和②梁长度均为L。计算时,单独取出图 6中横梁①部分进行分析,设杆件的节点位移分别为v1,θ1,v2,θ2,由两跨连续梁的对称性可知,横梁在节点2处转角为零,即θ2=0。
|
| 图 6 三跨弹性支承连续梁简化图Fig. 6 Simplification of 3-span continuous beam with elastic support |
利用势能极小值原理[6]求解3个位移值v1,θ1,v2和对应的弹簧支承力T1,T2与端部弯矩M,即:∂∏/∂δn=0,∏=U-W。
本次推导只求取弹簧支承力T1,T2,连续梁节点位移为{δ}=[v1θ1v2v1-θ1]T,结构总势能推导如下。
结构弯曲应变能为:
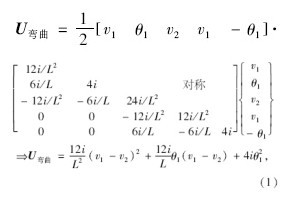
式中i=EI/L。
结构支座弹簧势能为:
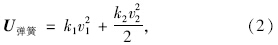
结构外力做功为:
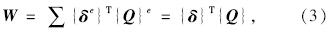
{Q}=[qL/2+Q1qL2/12qL+Q2L/2+Q1-qL2/12]T,
式中Q1,Q2为主桁传至横梁边、中支承处的节点力。
设P=qL/2,则:
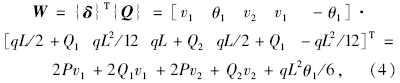
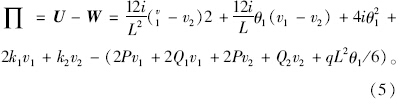
由∂∏/∂δi=0得到3个方程:
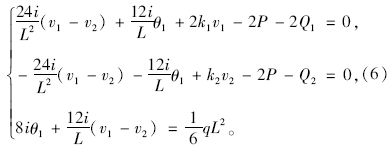
设M=qL2/12,代入式(6)得:
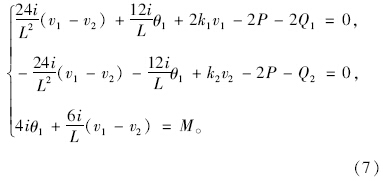
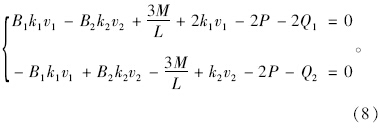
将式(8)第1式和第2式相加得:k2v2=4P+2Q1+Q2-2k1v1,代回第1式得:
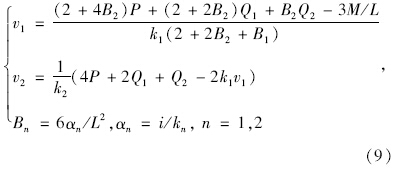
理想状态下,假设拉索索塔端无位移,设包含主桁支承弹簧反力在内的总支承反力为Tn,则:
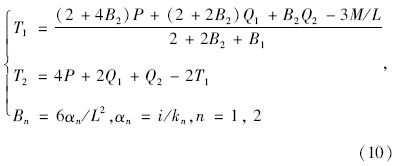
Tns=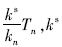 为拉索线刚度,n=1,2。
为拉索线刚度,n=1,2。
在讨论索力差值Ts的影响因素时,当横梁支承刚度ki逐渐增大时,各支座支反力Tn将随之增大,最终使边、中支反力达到3∶10的关系:当拉索刚度ks逐渐增大时,边、中支反力差值Tn逐渐增大,由于kn=ks+kzh(kzh为主桁竖向刚度),所以三索面索力差Tns=ksTn/kn亦将随之增大,最终使边、中索面索力达到3∶10的关系;而当主桁竖向刚度kzh增大时,Tn随之增大,ks/kn随之减小,三索面索力差Tsn=ksTn/kn的变化规律不明显,情况较复杂,将在2.1中予以阐述。
实际上,线性条件下的拉索索力可表示为:
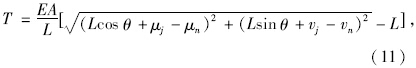
|
| 图 7 拉索拉力计算示意Fig. 7 Calculation diagram of stay-cable tensions |
在纵向,每片主桁可视为由多个杆件连接而成的弹性支承连续梁,梁上每个节点处有1个横向框架和3根拉索,因此分析清楚连续梁每个杆件荷载分配至节点的集中力情况很重要。传统铁路桥梁的桥面系一般设计成明桥面,而近年设计的桥梁系比较倾向于板桁组合结构,而板桁结构桥面一般与主桁焊接为一个整体,其纵横梁连接更趋刚性,从而使主桁节间荷载不能均匀地分配至两端节点,而是竖向位移小的一端节点力较大,竖向位移大的一端节点力较小。另外,在靠近主梁支座的1个节点,由于受到刚性支座的影响,该节点处的节点力比刚性节间总荷载值的1/2小。我们将节间荷载在两端节点分配不均匀的现象称为主梁刚度效应,该效应包括上述两种影响因素,即节点位移影响和支座影响,在钢桁梁桥设计时应予以考虑。
下面以刚性支承梁为例来阐述第2种影响因素,如图 8所示。
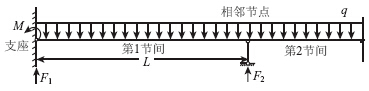
|
| 图 8 纵向荷载分配示意Fig. 8 Longitudinal load distribution |
每个节间荷载为qL,上图所示第1节间支反力为F11=5qL/8,F21=3qL/8,而相邻节点除由第1节间荷载产生的支反力F21外,还有第2节间荷载产生的支反力F22,大小近似等于qL/2,则该节点承受的节点力应为F2=F21+F22=0.875qL,但每个节间总荷载为qL,因此此处存在1个系数,计算时应考虑此种影响。
2 数值验算 2.1 横向验算
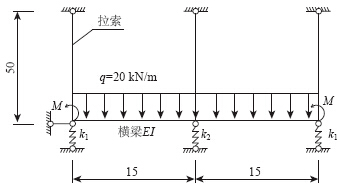
为了更好地阐述横向三索面索力差的影响因素,建立了如图 9的计算模型。模拟时,横梁采用梁单元,拉索采用桁架单元,所有杆件均不计自重,横梁自重以均布外荷载20 kN/m的方式施加,同时对横梁施加3个具有一定刚度的节点弹性支承,计算结果和式(10)的计算结果的对比见表 1、表 2。表 1为弹性支承刚度趋于零时,索力随拉索刚度的变化情况;表 2为拉索刚度一定时,索力随弹性支承刚度的变化情况,其中 不均衡系数表达式为:φn=[ΔTn/0.5(Tn中+Tn边)]×100%。ΔTn=Tn中-Tn边表示边中拉索索力差,Tn中和Tn边分别表示中索和边索索力。不均衡系数反映了边中索索力均衡程度,φn值越大,边中索力越不均匀,不均衡系数的正负反映了边中拉索索力大小关系,不均衡系数为正,表明中索索力大于边索索力;反之,表明中索索力小于边索索力。
|
| 图 9 验证模型(单位:m)Fig. 9 Verification model (unit: m) |
| i=EI/L | 索直径 d/m |
k= EA/L |
α=i/k | 有限元结果/kN | 公式结果/kN | ||
| T1 | T2 | T1 | T2 | ||||
| 9 270 | →0 | →0 | →+∞ | 200.00 | 200.00 | 200.00 | 200.00 |
| 9 270 | 0.10 | 3.06E+04 | 3.03E-01 | 113.56 | 372.89 | 113.55 | 372.91 |
| 9 270 | 0.12 | 4.41E+04 | 2.10E-01 | 113.24 | 373.52 | 113.23 | 373.54 |
| 9 270 | 0.14 | 6.01E+04 | 1.54E-01 | 113.05 | 373.91 | 113.04 | 373.93 |
| 9 270 | 0.16 | 7.84E+04 | 1.18E-01 | 112.92 | 374.16 | 112.91 | 374.18 |
| 9 270 | 0.18 | 9.93E+04 | 9.34E-02 | 112.83 | 374.33 | 112.83 | 374.35 |
| 9 270 | 0.20 | 1.23E+05 | 7.57E-02 | 112.77 | 374.45 | 112.76 | 374.47 |
| 9 270 | →+∞ | →+∞ | →0 | 112.50 | 375.00 | 112.50 | 375.00 |
| 拉索线 刚度i |
弹性支座 刚度kn |
公式结果/kN | 有限元结果/kN | 不均衡 系数φn |
||
| T1 | T2 | T1 | T2 | |||
| 3.06E+04 | →0 | 113.546 6 | 372.906 9 | 113.557 8 | 372.884 4 | 1.066 22 |
| 3.06E+04 | 500 | 111.706 5 | 366.950 1 | 111.717 6 | 366.928 0 | 1.066 39 |
| 3.06E+04 | 1 000 | 109.925 1 | 361.180 7 | 109.936 0 | 361.159 0 | 1.066 55 |
| 3.06E+04 | 1 500 | 108.199 6 | 355.590 0 | 108.210 4 | 355.568 5 | 1.066 71 |
| 3.06E+04 | 2 000 | 106.527 5 | 350.169 6 | 106.538 1 | 350.148 5 | 1.066 86 |
| 3.06E+04 | 5 000 | 97.487 7 | 320.827 1 | 97.497 4 | 320.807 7 | 1.067 69 |
| 3.06E+04 | 10 000 | 85.408 0 | 281.511 8 | 85.416 6 | 281.494 6 | 1.068 80 |
| 3.06E+04 | 100 000 | 26.437 3 | 87.814 7 | 26.440 0 | 87.809 2 | 1.074 30 |
| 3.06E+04 | 10 000 000 | 0.343 6 | 1.145 1 | 0.343 6 | 1.145 1 | 1.076 77 |
| 3.06E+04 | →+∞ | →0 | →0 | →0 | →0 | >1.076 77 |
通过表 1的数据对比发现:有限元计算结果与公式计算结果十分接近,随着拉索刚度与横梁刚度比值的增大,中、边索面索力差值随之增大,最后趋于10∶3的关系,当拉索刚度与横梁刚度比值趋于无限小时,中、边索面索力接近相等。
通过表 2的数据对比发现:有限元计算结果与公式计算结果十分接近,随着弹性支承刚度的增大,三索面索力不均衡系数随之增大,中、边索索力差逐渐增大。
通过上述计算分析可知:随着横梁弹性支承刚度的减小,或者结构横向联接系刚度的增大,三主桁三索面斜拉桥三索面索力将逐渐趋于均匀,同时随着弹性支承刚度的不断增大,拉索索力值相应地减小,这也是拉索索力从支座到跨中逐渐增大的原因。通过上述验算,可以证明第1节推导结果的正确性。
2.2 纵向分析
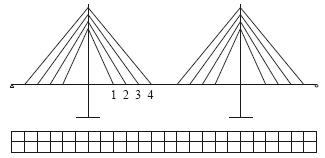
在纵向,主梁荷载或桥面荷载传至索梁锚固处节点的荷载随每个主梁节段单元两端节点位移大小变化,而每个节点处的集中荷载不全由该节点处的拉索承担,还由其他位置的拉索和主桁共同承担。下面针对自重作用下的三主桁三索面斜拉桥三索面索力横向分配的纵向影响因素,建立简单的计算模型,模型立面和主梁平面见图 10。
|
| 图 10 模型立面和主梁平面Fig. 10 Elevation of model and plane of main girder |
模型跨度布置为90 m +180 m +90 m,主塔高167 m,主梁宽30 m,节间长度为15 m,设16组拉索,每组索横向为3根,另外,模型主桁和横向联接系简化为单根梁单元,主梁杆件不计自重,全部以单元均布荷载替代,其中横梁为20 kN/m,主桁荷载为30 kN/m。
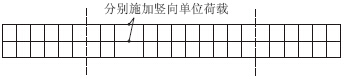
为了方便分析横梁荷载与主桁节点荷载的折减情况,计算时设两个工况。工况1:只作用横梁荷载;工况2:只作用主桁荷载。通过有限元计算得到一组索力值,利用第1节(1)推导出的式(9)反算得到产生相应拉索索力所需外荷载的大小,见式(12)~式(13),然后与实际施加的外荷载取比值,得到一个荷载变化系数。利用公式反算时,主桁对横梁的支承刚度计算方法为:去掉主梁节点处相应的横梁与单位力施加位置的拉索,分别在该主梁节点处边、中主桁上施加单位荷载,得到一个竖向位移,然后取其倒数即得该主梁节点处主桁对横梁的3个支承刚度值,如图 11所示,支承刚度值列于表 3,表中位置见图 10。
|
| 图 11 纵向支承刚度的求取示意Fig. 11 Schematic diagram of calculating longitudinalsupport stiffness |
| 位置 | 1 | 2 | 3 | 4 |
| 中桁 | 3.09E+04 | 3.31E+04 | 3.04E+04 | 2.49E+04 |
| 边桁 | 1.86E+04 | 2.07E+04 | 1.82E+04 | 1.35E+04 |
由式(1)~式(10)反算得到的外力值公式为:
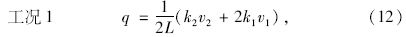
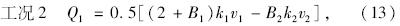
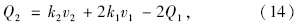
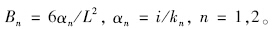
实际上,如果将斜拉桥主桁在顺桥向看成多跨刚性支承连续梁,则主桁传至其两端节点的集中力Q1与Q2大小应为1个节间外荷载值的1/2(靠近支座一个节点除外),横梁上的外荷载也不会发生变化。但斜拉桥一般被近似看成弹性支承连续梁结构,每个节间荷载传至两端节点处的力并不均匀,存在一定的偏差,这种现象即为第1.2节中所阐述的位移影响因素影响下的节点力不均匀分配现象。
对此,引入刚度系数,即弹性支承条件下的主桁节点力与刚性支承条件下的主桁节点力的比值。其值的大小反映了外荷载传至主梁节点处的力受主梁两端节点位移的影响程度。在本例中,均布载刚度系数为经公式反推求得的均布载值与实际施加的均布载值之比,节点力刚度系数为经公式反推求得的节点力值与刚性支承条件下计算出的节点力值之比。工况1计算结果见表 4,工况2计算结果见表 5。
| 位置 | 主桁位移值/m | 反算横梁均布载/ (kN·m-1) |
外加均布载/ (kN·m-1) |
刚度系数 | |
| v边 | v中 | ||||
| 1 | 0.009 | 0.012 | 16.346 | 20 | 0.82 |
| 2 | 0.015 | 0.018 | 20.231 | 20 | 1.01 |
| 3 | 0.020 | 0.023 | 20.719 | 20 | 1.04 |
| 4 | 0.024 | 0.026 | 19.513 | 20 | 0.98 |
| 位置 | 主桁位移值/m | 反算节点力(横梁节点)/kN | 刚性支承节 点力/kN |
刚度系数 | |||
| v边 | v中 | 中桁节点处 | 边桁节点处 | 中桁节点处 | 边桁节点处 | ||
| 1 | 0.028 05 | 0.028 03 | 453.062 2 | 447.019 5 | 562.5 | 0.805 44 | 0.794 70 |
| 2 | 0.039 74 | 0.039 72 | 493.603 7 | 488.257 6 | 450.0 | 1.096 90 | 1.085 02 |
| 3 | 0.055 51 | 0.055 49 | 544.534 3 | 539.445 3 | 450.0 | 1.210 08 | 1.198 77 |
| 4 | 0.076 32 | 0.076 30 | 607.623 9 | 602.500 2 | 450.0 | 1.350 28 | 1.338 89 |
由表 4的数据可知:斜拉桥主梁节点处横截面等效成弹性支承连续梁之后,横梁上经有限元值反算出的均布外荷载值与实际施加的外荷载值十分接近(靠近支座1根横梁相差较大,主要原因是受到固定支座的影响),因此利用公式进行计算时,无需调整;
由表 5的数据可知:斜拉桥主梁节点处横截面等效成弹性支承连续梁之后,主桁上经有限元值反算出的节点力与刚性支承条件下计算出的节点力较为接近,两者比值从塔根至跨中逐渐增大。 3 结论
(1)利用简化公式对三主桁斜拉桥进行计算时,结果与数值分析吻合。主梁每个节点处的横梁荷载由全桥拉索和主梁共同承担,每个节点处横梁实际承担荷载不全为施加的外荷载,必须予以折减;纵向传至横梁的荷载为一个集中力,此集中力大小随纵向主梁单元两端节点位移的大小而变化,不再为1个节间荷载的1/2,必须进行相应调整。对此,文中引入1个刚度系数,对于单独取出的横梁,经刚度系数调整后,其计算结果与数值计算结果是吻合的,并利用该系数验证了公式的正确性和计算精度,另外,刚度系数与主梁两端节点位移的大小关系有关;
(2)三主桁三索面斜拉桥横向三索面索力分配是横向联接系刚度、拉索线刚度和主桁竖向刚度共同作用的结果,横梁在竖向由其节点处拉索、主桁和主梁其余位置拉索共同支承,承受的外荷载有横梁荷载和顺桥向传至横梁节点的集中荷载。在主梁横向,索力差随拉索刚度和主桁竖向刚度的增大而增大,随横向联接系(横梁、横联、平联)刚度的增大而减小。
| [1] | 尹一平. 大跨度三主桁高速铁路桥梁静力特性分析[D]. 武汉:华中科技大学,2008. YIN Yi-ping. Analysis of Static Characteristics of Long-span High-speed Railway Bridge with Three Main Trusses[D]. Wuhan:Huazhong University of Science and Technology,2008. |
| [2] | 秦顺全,高宗余,潘东发. 武汉天兴洲公铁两用长江大桥关键技术研究[J]. 桥梁建设,2007,37(1):1-4,20. QIN Shun-quan,GAO Zong-yu,PAN Dong-fa. Research of Key Techniques for Wuhan Tianxingzhou Changjiang River Rail-cum-Road Bridge[J]. Bridge Construction,2007,37(1):1-4,20. |
| [3] | 张敏. 南京大胜关长江大桥受力特性、计算方法、桥面疲劳和防腐问题研究[D]. 长沙:中南大学,2010. ZHANG Min. Research of Mechanical Characteristics, Calculation Method, Deck Fatigue and Corrosion Problems of Nanjin Dashengguan Yangtze River Bridge[D]. Changsha:Central South University,2010. |
| [4] | 韩衍群. 高速铁路三主桁道碴整体桥面板桁组合桥受力特性及计算理论研究[D]. 长沙:中南大学,2008. HAN Yan-qun. Research of Mechanical Characteristics and Calculating Theory of Three-truss Plate-truss Composite High-speed Railway Bridges with Ballast Monolithic Deck[D]. Changsha: Central South University,2008. |
| [5] | 李的平. 三主桁三索面斜拉桥索力优化及空间受力性能研究[D]. 长沙:中南大学,2008. LI De-ping. Research of Cable Tension Optimization and Space Mechanics Behavior of Three Cable Planes Three Main Trusses Cable-stayed Bridge[D]. Changsha: Central South University,2008. |
| [6] | 赵经文,王宏钰. 结构有限元分析[M]. 北京:科学出版社,2001. ZHAO Jing-wen,WANG Hong-yu. Structural Finite Element Analysis[M]. Beijing:Science Press,2001. |
| [7] | 鲍莉霞. 三主桁结构内力分配影响因素研究[J]. 桥梁建设,2010 (4):40-42. BAO Li-xia. Study of Factors Having Influence on Internal Force Distribution of Three Main Trusses Structure[J]. Bridge Construction,2010 (4):40-42. |
| [8] | 王新敏. ANSNS工程结构数值分析[M]. 北京:人民交通出版社,2007. WANG Xin-min. ANSNS Engineering Structure Numerical Analysis[M]. Beijing:China Communications Press,2007. |
| [9] | 杜正国. 结构力学教程[M]. 成都:西南交通大学出版社,2004. DU Zheng-guo. Structural Mechanics Course[M]. Chengdu:Southwest Jiaotong University Press,2004. |
| [10] | 吴冲. 现代钢桥(上册)[M]. 北京:人民交通出版社,2008. WU Chong. Modern Steel Bridge (I)[M]. Beijing:China Communications Press,2008. |
| [11] | 易炳疆.三主桁三索面斜拉桥内力横向分配与桥型特点研究[D]. 成都:西南交通大学,2013. YI Bing-jiang. Transverse Distribution & Structural Behavior of Cable-stayed Bridge with Three Trusses and Three Cable Planes[D]. Chengdu:Southwest Jiaotong University Press,2013. |
| [12] | 胡汉舟,刘自明,秦顺全,等. 武汉天兴洲公铁两用长江大桥技术总结[M]. 北京:中国铁道出版社,2009. HU Han-zhou,LIU Zi-ming,QIN Shun-quan,et al. Technical Summary of Wuhan Tianxingzhou Highway-railway Yangtze River Bridge[M]. Beijing:China Railway Press,2009. |
| [13] | 王俭槐. 桁梁空间分析的薄壁箱梁法[J]. 铁道标准设计,1986 (3):1-7. WANG Jian-huai. Thin-walled Box Girder Method Using in Space Analysis of Trusses[J]. Railway Standard Design,1986 (3):1-7. |
| [14] | 林国雄,方秦汉. 芜湖长江大桥设计与关键技术研究[J]. 桥梁建设,1998 (4):1-8. LIN Guo-xiong, FANG Qing-han. Design of Wuhu Changjiang Bridge and Research on Its Key Technical Problems[J]. Bridge Construction,1998 (4):1-8. |
| [15] | 小西一郎.钢桥[M]. 朱立冬,等译.北京:人民交通出版社,1980. KONISHI I. Steel Bridge[M]. ZHU Li-dong, et al. translated. Beijing:China Communications Press,1980. |
| [16] | 肖海珠. 京沪高速南京长江大桥主桥静力特性[D]. 上海:同济大学,2007. XIAO Hai-zhu. Static Characteristics of Main Bridge of Nanjing Yangtze River Bridge on Beijing-Shanghai High-speed Railway[D]. Shanghai:Tongji University,2007. |
 2015, Vol. 31
2015, Vol. 31

